【深度学习-吴恩达】L1-2 神经网络基础
L1 深度学习概论
2 神经网络基础
课程视频共145min6s
2.1 二分分类
Binary Classification
一些表示方法
- m:数据集的规模
- mtrain :训练集规模
- mtest:测试集规模
- nx:输入特征向量的维度,简写为n
- (x, y):一组单独训练样本
- y:在二分类中,0/1的输出结果,即y∈{0, 1}
- x:nx维度的输入特征向量,即x∈Rnx
- 训练集:{(x(1), y(1)), (x(2), y(2)), …, (x(m), y(m))}
- X=[x(1), x(2), …, x(m)]
- X ∈ Rnx × m
- X.shape=(nx, m)
- Y=[y(1), y(2), …, y(m)]
- Y∈R1×m
- Y.shape = (1, m)
- X=[x(1), x(2), …, x(m)]
2.2 Logisitc回归
logistic回归:二分分类算法,输出标签0/1
Given x, want y ^ \hat{y} y^ = P(y = 1 | x)
若线性回归,则 y ^ \hat{y} y^ = wTx + b
- 值不会在[0, 1]之间,可以很大或者负值
Sigmoid函数, y ^ = σ ( w T x + b ) \hat{y} = \sigma(w^Tx + b) y^=σ(wTx+b)
-
σ ( z ) = 1 1 + e − z \sigma(z) = \frac{1}{1 + e^-z} σ(z)=1+e−z1
-
0到1之间
-
极限接近0或者1
-
学习参数 w w w和 b b b
-
另一种表示方式(不重要)
-
y ^ = σ ( θ T x ) \hat{y} = \sigma(\theta^Tx) y^=σ(θTx)
-
其中输入x默认x0 = 1,所以x∈Rnx+1
-
θ T = ( θ 0 θ 1 ⋮ θ n x ) \theta^T = \left( \begin{matrix} \theta_0\\ \theta_1\\ \vdots\\ \theta_{n_x} \end{matrix} \right) θT=⎝ ⎛θ0θ1⋮θnx⎠ ⎞
-
其中 θ 0 \theta_0 θ0与x0相乘,即为b
-
θ 1 \theta_1 θ1到 θ n x \theta_{n_x} θnx即为 w T w^T wT
-
2.3 Logistic回归损失函数
使用上标 ( i ) (i) (i)来指明数据
- σ ( z ( i ) ) = 1 1 + e − z ( i ) \sigma(z^{(i)})= \frac{1}{1 + e^{-z^{(i)}}} σ(z(i))=1+e−z(i)1
损失函数 L ( y ^ − y ) L(\hat{y} - y) L(y^−y) loss function
-
适用于单个训练样本
-
L ( y ^ − y ) = − ( y l o g y ^ + ( 1 − y ) l o g ( 1 − y ^ ) ) L(\hat{y}-y) = -(ylog\hat{y} + (1-y)log(1-\hat{y})) L(y^−y)=−(ylogy^+(1−y)log(1−y^))
- 若y = 1,则 L ( y ^ − y ) = − l o g y ^ L(\hat{y}-y) = -log\hat{y} L(y^−y)=−logy^
- 损失函数较小,则期望 y ^ \hat{y} y^较大,接近1
- 若y = 0,则 L ( y ^ − y ) = l o g ( 1 − y ^ ) L(\hat{y}-y) = log(1-\hat{y}) L(y^−y)=log(1−y^)
- 损失函数较小,则期望 y ^ \hat{y} y^较小,接近0
- 若y = 1,则 L ( y ^ − y ) = − l o g y ^ L(\hat{y}-y) = -log\hat{y} L(y^−y)=−logy^
成本函数 cost function
-
参数的总成本
-
J ( w , b ) = 1 m ∑ i = 1 m L ( y ^ ( i ) − y ( i ) ) = − 1 m ∑ i = 1 m ( y ( i ) l o g y ^ ( i ) + ( 1 − y ( i ) ) l o g ( 1 − y ^ ( i ) ) ) J(w,b) = \frac{1}{m}\sum_{i = 1}^{m} L(\hat{y}^{(i)} - y^{(i)}) = -\frac{1}{m}\sum_{i=1}^{m}(y^{(i)}log\hat{y}^{(i)} + (1-y^{(i)})log(1-\hat{y}^{(i)})) J(w,b)=m1i=1∑mL(y^(i)−y(i))=−m1i=1∑m(y(i)logy^(i)+(1−y(i))log(1−y^(i)))
2.4 梯度下降法
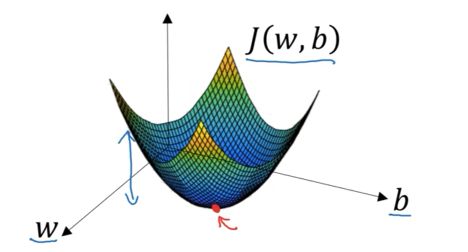
希望找到最小的$J(w,b) $
$J(w,b) $是一个凸函数,由此从任何初始点,容易获得相似的最终位置,即全局最优解
w : = w − α d J ( w , b ) d w b : = b − α d J ( w , b ) d b w:= w - \alpha\frac{dJ(w,b)}{dw}\\ b:= b - \alpha\frac{dJ(w,b)}{db} w:=w−αdwdJ(w,b)b:=b−αdbdJ(w,b)
-
α \alpha α:学习率
-
更新 w , b w,b w,b,迭代学习,直到最优点
-
求导严格来讲,两个及以上变量时候,应该使用 ∂ \partial ∂
-
编程时候常使用dw、db变量
2.5 导数
f ( a ) = 3 a f(a) = 3a f(a)=3a
d d a f ( a ) = 3 \frac{d}{da}f(a)=3 dadf(a)=3
derivative 导数
slope 斜率
2.6 导数2
f ( a ) = a 2 f(a) = a^2 f(a)=a2 d d a f ( a ) = 2 a \frac{d}{da}f(a)=2a dadf(a)=2a
f ( a ) = 3 a f(a) = 3a f(a)=3a d d a f ( a ) = 3 \frac{d}{da}f(a)=3 dadf(a)=3
f ( a ) = l n ( a ) f(a) = ln(a) f(a)=ln(a) d d a f ( a ) = 1 a \frac{d}{da}f(a)=\frac{1}{a} dadf(a)=a1
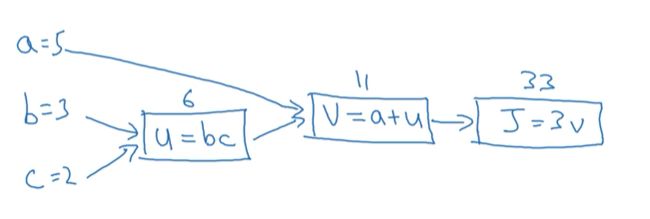
2.7 计算图
J ( a , b , c ) = 3 ( a + b c ) J(a,b,c) = 3(a+bc) J(a,b,c)=3(a+bc)
计算图:从左到右的计算
2.8 使用计算图求导
导数:计算图从右到左计算
链式法则
d J d v = 3 \frac{dJ}{dv}=3 dvdJ=3
d J d a = 3 \frac{dJ}{da} = 3 dadJ=3
d J d u = 3 \frac{dJ}{du}=3 dudJ=3
d J d b = 3 c \frac{dJ}{db}=3c dbdJ=3c
一些编程时候,想要最终结果的某个导数 d F i n d O u t p u t V a r d v a r \frac{dFindOutputVar}{dvar} dvardFindOutputVar通常记作dvar变量
2.9 Logistic回归中的梯度下降法
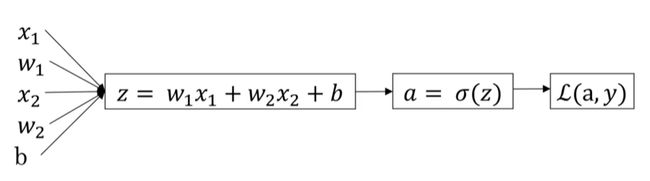
logistic回归回顾
- z = w T x + b z=w^Tx+b z=wTx+b
- y ^ = a = σ ( z ) \hat{y}=a=\sigma(z) y^=a=σ(z)
- L ( a , y ) = − ( y l o g ( a ) + ( 1 − y ) l o g ( 1 − a ) ) L(a,y) = -(ylog(a) + (1-y)log(1-a)) L(a,y)=−(ylog(a)+(1−y)log(1−a))
两个输入特征的计算图
变量da = d L ( a , y ) d a = − y a + 1 − y 1 − a \frac{dL(a,y)}{da} = -\frac{y}{a} + \frac{1-y}{1-a} dadL(a,y)=−ay+1−a1−y
变量dz = d L d z = a − y \frac{dL}{dz} = a-y dzdL=a−y
变量dw1 = d L d w 1 = x 1 ( a − y ) \frac{dL}{dw_1}=x_1(a-y) dw1dL=x1(a−y)
变量dw2 = d L d w 1 = x 2 ( a − y ) \frac{dL}{dw_1}=x_2(a-y) dw1dL=x2(a−y)
变量db = d L d w 1 = a − y \frac{dL}{dw_1}=a-y dw1dL=a−y
单样本的梯度下降法求解:
$w_1:= w_1 - \alpha\frac{dL}{dw_1}\$
$w_2:= w_2 - \alpha\frac{dL}{dw_2}\$
$b:= b - \alpha\frac{dL}{db}\$
2.10 多样本的梯度下降法
$J(w,b) = \frac{1}{m}\sum_{i = 1}^{m} L(a^{(i)} - y^{(i)}) $
- 所有样本损失函数的平均值
a ( i ) = y ^ ( i ) = σ ( w T x ( i ) + b ) a^{(i)} = \hat{y}^{(i)}=\sigma(w^Tx^{(i)}+b) a(i)=y^(i)=σ(wTx(i)+b)
∂ ∂ w 1 J ( w , b ) = 1 m ∑ i = 1 m ∂ ∂ w 1 L ( a ( i ) − y ( i ) ) \frac{\partial}{\partial w_1}J(w,b) = \frac{1}{m}\sum_{i = 1}^{m}\frac{\partial}{\partial w_1} L(a^{(i)} - y^{(i)}) ∂w1∂J(w,b)=m1i=1∑m∂w1∂L(a(i)−y(i))
一个例子
J = 0 , d w 1 = 0 , d w 2 = 0 , d b = 0 J=0, dw_1=0, dw_2=0, db=0 J=0,dw1=0,dw2=0,db=0
For i=1 to m
z ( i ) = w T x ( i ) + b \quad z^{(i)}=w^Tx{(i)}+b z(i)=wTx(i)+b
a ( i ) = σ ( z ( i ) ) \quad a^{(i)}=\sigma(z^{(i)}) a(i)=σ(z(i))
J + = − ( y ( i ) l o g ( a ( i ) ) + ( 1 − y ( i ) ) l o g ( 1 − a ( i ) ) ) \quad J += -(y^{(i)}log(a^{(i)}) + (1-y^{(i)})log(1-a^{(i)})) J+=−(y(i)log(a(i))+(1−y(i))log(1−a(i)))
d z ( i ) = a ( i ) − y ( i ) \quad dz^{(i)} = a^{(i)}-y^{(i)} dz(i)=a(i)−y(i)
d w 1 + = x 1 ( i ) d z ( i ) \quad dw_1+= x_1^{(i)}dz^{(i)} dw1+=x1(i)dz(i)
d w 2 + = x 2 ( i ) d z ( i ) \quad dw_2+= x_2^{(i)}dz^{(i)} dw2+=x2(i)dz(i)
d b + = d z ( i ) \quad db += dz^{(i)} db+=dz(i)
J / = m J /= m J/=m
d w 1 / = m ; d w 1 / = m ; d b / = m dw_1/= m;dw_1/=m;db/=m dw1/=m;dw1/=m;db/=m
w 1 : = w 1 − α d w 1 w_1:= w_1 - \alpha dw_1 w1:=w1−αdw1
w 2 : = w 2 − α d w 2 w_2:= w_2 - \alpha dw_2 w2:=w2−αdw2
b : = b − α b b:= b - \alpha b b:=b−αb
- 两个缺点
- 需要两个循环,一个循环m个样本,另一个循环n个特征
- 显式使用for循环效率较低
- 使用向量化进行优化
- ?另一个缺点没说
- 需要两个循环,一个循环m个样本,另一个循环n个特征
2.11 向量化
Vectorization
非向量化版本
z = 0
for i in range(nx):
z += w[i]*x[i]
z += b
向量化版本
z = np.dot(w, x) + b
- GPU和CPU都有并行化指令SIMD
- 单指令流多数据流
- numpy能充分利用并行化提速,而不要显式使用for循环
2.12 向量化2
避免for循环
-
计算en矩阵
u = np.exp(v)
-
计算log值
np.log(v)
-
计算绝对值
np.abs(v)
-
计算最大值
np.maxinum(v)
logistic回归非向量化版本
J = 0 , d w 1 = 0 , d w 2 = 0 , d b = 0 J=0, dw_1=0, dw_2=0, db=0 J=0,dw1=0,dw2=0,db=0
For i=1 to m
z ( i ) = w T x ( i ) + b z^{(i)}=w^Tx{(i)}+b z(i)=wTx(i)+b
a ( i ) = σ ( z ( i ) ) a^{(i)}=\sigma(z^{(i)}) a(i)=σ(z(i))
J + = − ( y ( i ) l o g ( a ( i ) ) + ( 1 − y ( i ) ) l o g ( 1 − a ( i ) ) ) J += -(y^{(i)}log(a^{(i)}) + (1-y^{(i)})log(1-a^{(i)})) J+=−(y(i)log(a(i))+(1−y(i))log(1−a(i)))
d z ( i ) = a ( i ) − y ( i ) dz^{(i)} = a^{(i)}-y^{(i)} dz(i)=a(i)−y(i)
d w 1 + = x 1 ( i ) d z ( i ) dw_1+= x_1^{(i)}dz^{(i)} dw1+=x1(i)dz(i)
d w 2 + = x 2 ( i ) d z ( i ) dw_2+= x_2^{(i)}dz^{(i)} dw2+=x2(i)dz(i)
d b + = d z ( i ) db += dz^{(i)} db+=dz(i)
J /= m
d w 1 / = m ; d w 1 / = m ; d b / = m dw_1/= m;dw_1/=m;db/=m dw1/=m;dw1/=m;db/=m
w 1 : = w 1 − α d w 1 w_1:= w_1 - \alpha dw_1 w1:=w1−αdw1
w 2 : = w 2 − α d w 2 w_2:= w_2 - \alpha dw_2 w2:=w2−αdw2
b : = b − α d b b:= b - \alpha db b:=b−αdb
logistic回归向量化版本
J = 0 , d w = n p . z e r o s ( ( n x , 1 ) ) , d b = 0 J=0, dw=np.zeros((n_x,1)), db=0 J=0,dw=np.zeros((nx,1)),db=0
For i=1 to m
z ( i ) = w T x ( i ) + b z^{(i)}=w^Tx{(i)}+b z(i)=wTx(i)+b
a ( i ) = σ ( z ( i ) ) a^{(i)}=\sigma(z^{(i)}) a(i)=σ(z(i))
J + = − ( y ( i ) l o g ( a ( i ) ) + ( 1 − y ( i ) ) l o g ( 1 − a ( i ) ) ) J += -(y^{(i)}log(a^{(i)}) + (1-y^{(i)})log(1-a^{(i)})) J+=−(y(i)log(a(i))+(1−y(i))log(1−a(i)))
d z ( i ) = a ( i ) − y ( i ) dz^{(i)} = a^{(i)}-y^{(i)} dz(i)=a(i)−y(i)
d w + = x ( i ) d z ( i ) dw+= x^{(i)}dz^{(i)} dw+=x(i)dz(i)
d b + = d z ( i ) db += dz^{(i)} db+=dz(i)
J /= m
d w / = m ; d b / = m dw/=m;db/=m dw/=m;db/=m
w 1 : = w 1 − α d w 1 w_1:= w_1 - \alpha dw_1 w1:=w1−αdw1
w 2 : = w 2 − α d w 2 w_2:= w_2 - \alpha dw_2 w2:=w2−αdw2
b : = b − α d b b:= b - \alpha db b:=b−αdb
2.13 向量化3
计算正向传播
Z = [ z ( 1 ) z ( 2 ) … z ( m ) ] = w T X + [ b b … b ] = [ w T x ( 1 ) + b w T x ( 2 ) + b … w T x ( m ) + b ] Z = [z^{(1)}z^{(2)}\dots z^{(m)}]\\ = w^TX+[bb\dots b]\\ = [w^Tx^{(1)} + b\space\space\space w^Tx^{(2)} + b \space\space\space \dots \space\space\space w^Tx^{(m)} + b] Z=[z(1)z(2)…z(m)]=wTX+[bb…b]=[wTx(1)+b wTx(2)+b … wTx(m)+b]
在b为常数时候,由此使用一行代码可以进行计算,无需使用for循环:
Z = np.dot(w^T, X) + b
其中b为常数,在Python中会广播为1×m向量
2.14 向量化4
同时计算m个数据集参数
非向量法:
- dZ定义:
d z ( 1 ) = a ( 1 ) − y ( 1 ) d z ( 2 ) = a ( 2 ) − y ( 2 ) ⋮ d z ( m ) = a ( m ) − y ( m ) d Z = [ d z ( 1 ) d z ( 2 ) … d z ( m ) ] dz^{(1)} = a^{(1)} - y^{(1)}\\ dz^{(2)} = a^{(2)} - y^{(2)}\\ \vdots\\ dz^{(m)} = a^{(m)} - y^{(m)}\\ dZ = [dz^{(1)}\quad dz^{(2)}\quad \dots \quad dz^{(m)}]\\\\ dz(1)=a(1)−y(1)dz(2)=a(2)−y(2)⋮dz(m)=a(m)−y(m)dZ=[dz(1)dz(2)…dz(m)] - dZ用A和Y表示
A = [ a ( 1 ) … a ( m ) ] Y = [ y ( 1 ) … y ( m ) ] = > d Z = A − Y = [ a ( 1 ) − y ( 1 ) … a ( m ) − y ( m ) ] A = [a^{(1)}\dots a^{(m)}]\qquad Y = [y^{(1)}\dots y^{(m)}]\\ => dZ = A - Y = [a^{(1)}\!-\!y^{(1)}\space\dots\space a^{(m)}\!-\!y^{(m)}]\\\\ A=[a(1)…a(m)]Y=[y(1)…y(m)]=>dZ=A−Y=[a(1)−y(1) … a(m)−y(m)] - 计算dw
d w = 0 d w 1 + = x 1 ( 1 ) d z ( 1 ) d w 2 + = x 2 ( 2 ) d z ( 2 ) ⋮ d w n + = x n ( n ) d z ( n ) d w / = d w 计算 d b d b + = d z ( 1 ) d b + = d z ( 2 ) ⋮ d b + = d z ( n ) dw=0\\ dw_1+= x_1^{(1)}dz^{(1)}\\ dw_2+= x_2^{(2)}dz^{(2)}\\ \vdots\\ dw_n+= x_n^{(n)}dz^{(n)}\\ dw /= dw\\\\ 计算db\\ db += dz^{(1)}\\ db += dz^{(2)}\\ \vdots\\ db += dz^{(n)} dw=0dw1+=x1(1)dz(1)dw2+=x2(2)dz(2)⋮dwn+=xn(n)dz(n)dw/=dw计算dbdb+=dz(1)db+=dz(2)⋮db+=dz(n) - 向量法:
d b = 1 m ∑ i = 1 m d z ( i ) = 1 m n p . s u m ( d Z ) d w = 1 m X d Z T = 1 m [ x ( 1 ) … x ( m ) ] [ d z ( 1 ) … d z ( m ) ] T db = \frac{1}{m}\sum_{i=1}^mdz^{(i)}=\frac{1}{m}np.sum(dZ)\\ dw=\frac{1}{m}XdZ^T=\frac{1}{m}[x^{(1)}\dots x^{(m)}][dz^{(1)}\dots dz^{(m)}]^T db=m1i=1∑mdz(i)=m1np.sum(dZ)dw=m1XdZT=m1[x(1)…x(m)][dz(1)…dz(m)]T
具体实现:
For iter in range(1000): #多次迭代更新参数
Z = w T X + b = n p . d o t ( w T , x ) + b \quad Z = w^TX+b=np.dot(w^T,x)+b Z=wTX+b=np.dot(wT,x)+b
A = σ ( Z ) \quad A=\sigma(Z) A=σ(Z)
d Z = A − Y \quad dZ=A-Y dZ=A−Y
d w = 1 m X d Z T \quad dw=\frac{1}{m}XdZ^T dw=m1XdZT
d b = 1 m n p . s u m ( d Z ) \quad db=\frac{1}{m}np.sum(dZ) db=m1np.sum(dZ)
w : = w − α d w \quad w:=w-\alpha dw w:=w−αdw
b : = b − α d b \quad b:=b-\alpha db b:=b−αdb
2.15 Python中的广播
广播的例子
#求列的和,行使用axis=1
cal = A.sum(axis = 0)
percentage = 100 * A / (cal.reshape(1, 4))
统用法则
- m*n矩阵,进行加法或者减法
- (1, n) / (m, 1) -> (m, n)
2.16 Python Numpy的说明
优势
- 语言表现能力更强
劣势
- 容易出现细微的错误
尽量避免使用秩为1的矩阵
2.17 Jupyter使用指南
作业链接:https://www.heywhale.com/home/column/5e8181ce246a590036b875f9
2.18 Logistic损失函数解释
损失函数 L L L
-
If y=1: P(y|x) = y ^ \hat{y} y^
-
If y=0: P(y|x) = 1 − y ^ 1-\hat{y} 1−y^
-
P ( y ∣ x ) = y ^ y ( 1 − y ^ ) ( 1 − y ) P(y|x) = \hat{y}^y(1-\hat{y})^{(1-y)} P(y∣x)=y^y(1−y^)(1−y)
-
l o g P ( y ∣ x ) = y l o g y ^ + ( 1 − y ) l o g ( 1 − y ^ ) = − L ( y ^ , y ) logP(y|x) = ylog\hat{y} + (1-y)log(1-\hat{y}) = -L(\hat{y},y) logP(y∣x)=ylogy^+(1−y)log(1−y^)=−L(y^,y)
成本函数 J J J:
P ( l a b e l s i n t r a i n s e t ) = ∏ i = 1 m P ( x ( i ) ∣ y ( i ) ) l o g P ( l a b e l s i n t r a i n s e t ) = l o g ∏ i = 1 m P ( x ( i ) ∣ y ( i ) ) = − ∑ i = 1 m L ( y ^ ( i ) , y ( i ) ) J ( w , b ) = 1 m ∑ i = 1 m L ( y ^ ( i ) − y ( i ) ) P(labels\space in\space train\space set) = \prod_{i=1}^mP(x^{(i)}|y^{(i)})\\ log\space P(labels\space in\space train\space set) = log\prod_{i=1}^mP(x^{(i)}|y^{(i)})=-\sum_{i=1}^mL(\hat{y}^{(i)},y^{(i)})\\ J(w,b) = \frac{1}{m}\sum_{i = 1}^{m} L(\hat{y}^{(i)} - y^{(i)}) P(labels in train set)=i=1∏mP(x(i)∣y(i))log P(labels in train set)=logi=1∏mP(x(i)∣y(i))=−i=1∑mL(y^(i),y(i))J(w,b)=m1i=1∑mL(y^(i)−y(i))