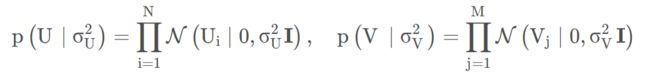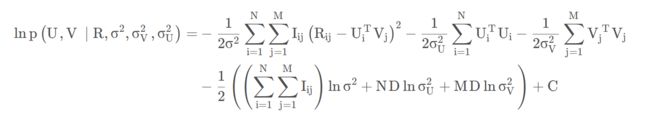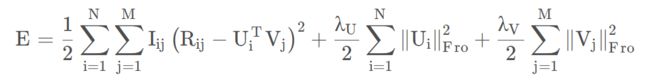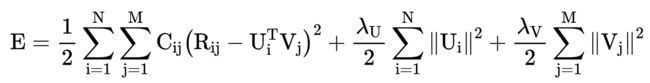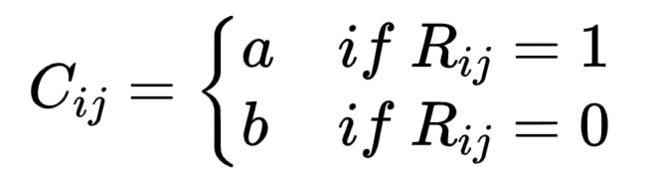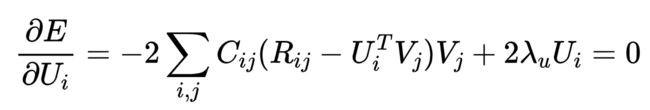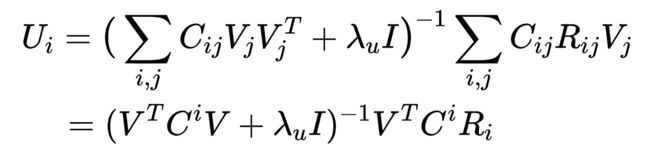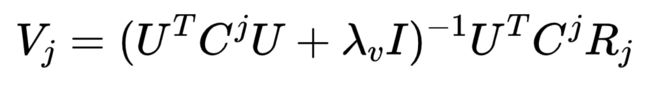概率矩阵分解及ALS算法实现
推荐系统中最为主流与经典的技术之一是协同过滤技术（Collaborative Filtering），其中基于模型的协同过滤技术中尤为矩阵分解（Matrix Factorization）技术最为普遍和流行，因为它的可扩展性极好并且易于实现。矩阵分解在协同过滤共现矩阵的基础上，使用更稠密的隐向量表示用户和物品，挖掘用户和物品的隐含兴趣和隐含特征。
一、矩阵分解（Matrix Factorization，MF）
模型背后的思想是，用户的态度或偏好由少数不可观测的因素决定。例如，对于N个用户和M个电影，N×M的偏好矩阵R由一个N×D的用户系数矩阵U和一个D×M的因子矩阵V的乘积给出。训练这样的模型相当于在给定的损失函数下找到观测的N × M目标矩阵R的最佳秩D的近似值。
基于最小化距离平方和的低秩近似可以通过奇异值分解( Singular Value Decomposition，SVD )找到。SVD寻找给定秩的矩阵
，使
到目标矩阵R的距离平方和最小。需要优化的目标函数（也即损失函数）如下：
其中， 
是一个指示函数，如果用户i对电影j进行了评分，那么
;否则为0。
二、概率矩阵分解（Probabilistic Matrix Factorization，PMF）
由于大多数真实数据集是稀疏的，R中的大多数条目会缺失。在这种情况下，距离平方和只针对目标矩阵R的观测值计算。总的来说，MF会有两个问题：
不能很好地处理规模非常大的数据。
不能很好地处理那些非常少做评价的用户。
为解决上述问题，多伦多大学计算机的两位学者于2007年提出了概率矩阵分解模型[1]。
１. PMF基本模型描述
假设有M部电影，N个用户，和从1到K 的整数评价值。让
代表用户i电影j的评分，
和
是潜在的用户和电影特征矩阵，其中行向量
和 
分别表示特定用户的和特定电影的潜在特征向量。然后做了两个假设。
假设一 观测噪声（观测评分矩阵R和近似评分矩阵
之差）满足高斯分布
其中， 为指示函数：如果用户i已经对商品j进行了评分，则为1,否者为0；
是观测噪声的方差，属于人工设定的超参数。
假设二 用户潜在特征向量和商品潜在特征向量都服从均值为0的高斯先验分布
其中，这里的
表示一个对角阵； 
, 
是先验噪声的方差，属于人工设定的超参数。
综合以上三个概率密度函数，利用经典的后验概率推导，可以得到：
其中C是一个不依赖于参数的常数。在超参数（即观察噪声方差和先验噪声方差）保持不变的情况下，最大化对数后验概率（即上式），相当于最小化具有二次正则项的误差平方和目标函数：
其中 
, 
，
又称F-范数, 即矩阵中每项数的平方和的开方值。
从上式中可以看出，PMF的目标函数只是比MF的目标函数中多了U和V的二次正则项。
２. 隐式反馈中的PMF模型
上述PMF基本模型使用的是显式评分，比如 MovieLens 数据集中的 1-5 分或是豆瓣上的 1 到 5 星。这些评分很能反映用户对物品的偏好，像豆瓣上打 5 星表示力荐，打 1 星表示很差。相较而言，隐式反馈数据大都来源于用户的行为，如物品的购买记录，网页的浏览记录，视频的观看时长、科研文章的收藏等等。隐式反馈一般有如下特点：
(1) 数据总量大。比如很多人都在淘宝上买东西留下记录，却很少人会去给好评差评；每天在网上浏览了很多文章，却很少点赞。
(2) 没有负反馈。这点是比较致命的，比如看过一部电影代表对其的偏好，但若没看过一部电影并不代表不喜欢这部电影，可能是在待观看列表里面，然而从数据中这一点无法得知，这导致数据的噪音大。而如果只用有反馈的数据进行建模，会导致严重的过拟合。
如上面第一点所述，实际生活中显式反馈的评分数据是比较少的，而隐式反馈数据却非常丰富，因而重要性越来越高。为了解决其没有负反馈的问题，这里采用 Hu 等人[2]在论文《Collaborative Filtering for Implicit Feedback Datasets》中描述的方法，引入用户对于物品的偏好系数：
表示用户对物品的反馈，如购买、搜索等行为，上式表明只要有反馈，皆为1 。此外还引入用户对于物品的置信度
， 可以看出即使为零， 
也不为零，并且随着的增长而增长。 于是写出目标函数：
对于置信度的设置，王崇[3]在研究科研文章推荐时，认为用户文章库中的的数据置信度高，即
的数据置信度高；相反，
的数据既可以解释成用户不感兴趣，也可以解释成用户没看到过该文章。这和one-class协同过滤问题一样，作者使用相同的策略来设置：
其中,a,b是超参数，通过调参来满足a>b>0。
3. 优化方法
目前主流的方法有两种：随机梯度下降 (简称 SGD，stochastic gradient decent) 和交替最小二乘法 (简称 ALS，alternating least squares)，而本文的重点是后者。ALS算法可以进行分布式并行计算，并且没有SGD中学习率的选择问题。
不同于SGD的逐渐迭代，ALS是一种直接法。由于目标函数 和都未知，所以该函数非凸，难以直接优化。然而如果将所有的固定住视其为常数，那么就变成了一个 关于 的最小二乘问题，可以直接求出解析解。于是可以先固定求出，再固定求出，二者不断交替，这个流程不断重复直至收敛。因而 ALS 全称为交替最小二乘法 (alternating least squares)，这其实有点类似于 EM 算法中 E 步和 M 步的交替求解。
其中为所有物品隐向量组成的矩阵; 
为对角矩阵，其对角线上的元素为用户对所有物品的置信度, 
; 
为用户对所有物品的评分（也即偏好）。
上式中
的计算复杂度为
, 在 M很大的情况下是难以承受的。实现上注意要采取降低复杂度的方法。
同理，固定U 对 求偏导得：
代码实现：https://github.com/hulongmao/PMF_ALS。
参考文献：
[1] Salakhutdinov R . Probabilistic Matrix Factorization. Curran Associates Inc. 2007.
[2] Hu Y , Koren Y , Volinsky C . Collaborative Filtering for Implicit Feedback Datasets[C]// Eighth IEEE International Conference on Data Mining. IEEE, 2009.
[3] Wang C, Blei D M. Collaborative topic modeling for recommending scientific articles[C]//Proceedings of the 17th ACM SIGKDD international conference on Knowledge discovery and data mining. 2011: 448-456.
[4]Probabilistic Matrix Factorization（概率矩阵分解）https://blog.csdn.net/kangxiatao/article/details/109803030
[5]共轭梯度法求解协同过滤中的 ALS https://zhuanlan.zhihu.com/p/88139448
[6]KDD'21 | 时间检验研究奖论文解读 https://zhuanlan.zhihu.com/p/416670663