Floyd算法的应用

Floyd算法

Floyd算法又称为弗洛伊德算法、插点法， 是解决给定的加权图中顶点间的最短路径的一种算法，可以正确处理有向图或负权的最短路径问题，同时也被用于计算有向图的传递闭包。

算法过程

求一个n个点m条边的无向图，任意两点的距离

1. 二维数组 d[ ][ ] 记录有边相连的任意两点的距离，无边的两点赋值为正无穷（一个极大值， 一般用0x3f3f3f3f）如d[ i ][ j ] 表示顶点 i 到 j 的最短距离。

2. 通过从前往后枚举经过的中间点 k， 再枚举该条边的起点 i，和 终点 j， 来更新 顶点 i， j的之间最短距离。如图如果 i -> j 的权值大于 i -> k -> j 时 将更新i ，j 间的距离即d[ i ] [ j ] = max( d[ i ] [ j ] , d[ i ] [ k ] +d[ k ] [ j ] )
   

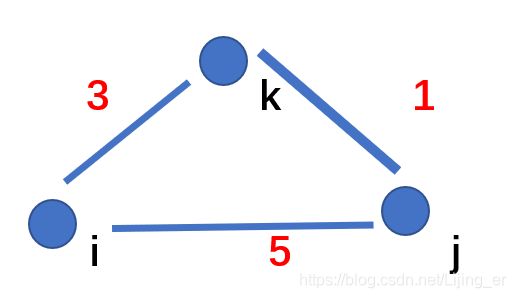
算法特点

时间复杂度：$$O（n^3）$$
适用范围：适用于无负权回路的稠密图， 运行一次即可求得任意两点间的最短路，由于时间复杂度过高， 一般用于数据范围不大的题目。

特点： 由于枚举中间点 ki 时，是从前往后枚举， 所以当求到ui， vi之间的距离时， 除起点 ui和 终点 vi 外所经过的顶点一定都是小于k的。

最短路问题

求最短路是Floyd最朴素的做法，与上述描述相同，代码如下

memset(d,0x3f,sizeof d);
/*
输入数据 更新d[i][j]
*/
for(int k=1; k<=n; k++){
     for(int i=1; i<=n; i++){
         for(int j=1; j<=n; j++){
             d[i][j]=min(d[i][j], d[i][k]+d[k][j]);
         }
     }
 }

求传递闭包

什么是传递闭包

定义: 对于任何关系 R，R 的传递闭包总是存在的。传递关系的任何家族的交集也是传递的。进一步的，至少存在一个包含 R 的传递关系，也就是平凡的: X × X。R 传递闭包给出自包含 R 的所有传递关系的交集。

人话就是， 在一个有向图中，求点与点之间的可到达的关系。
比如祖宗关系， A是B的祖宗，B是C的祖宗，那A与C之间的关系呢？显然A是C的祖宗。

利用Floyd-Warshall算法通过 枚举中间点， 通过中间点传递两点之间关系 的性质， 可以巧妙的求得传递闭包。

算法过程

给定一个n个点m条边的有向图， q次询问， 每次询问顶点 i 是否能够到达 顶点 j

过程上述求最短路的算法过程类似， 只是d[ ][ ]数组中存放的权值意义可能不同。

1. 二维数组 d[ ][ ] 记录任意两点是否可以到达，无法到达赋值为0， 可到达赋值为1 ， 例如d[ i ][ j ] 表示顶点 i 是否可以到达顶点 j 。

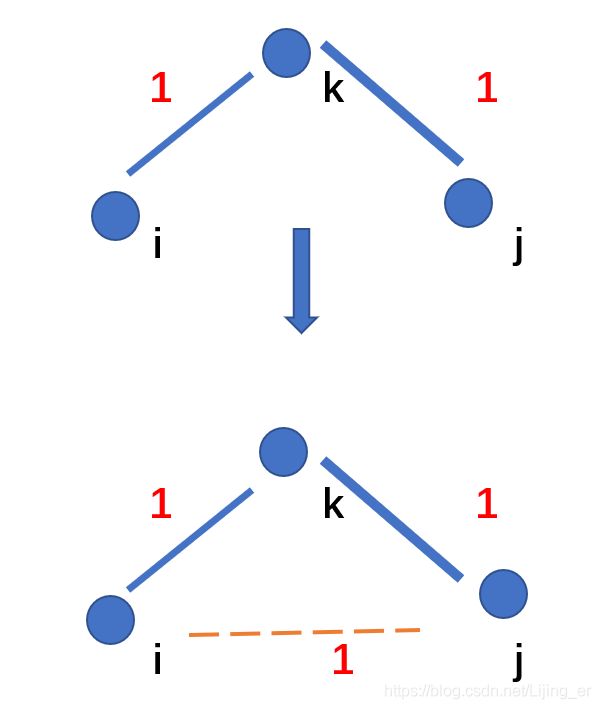
2. 通过从前往后枚举经过的中间点 k， 再枚举该条边的起点 i，和 终点 j， 来更新 顶点 i， j的之间的关系。如图如果 顶点i 本无法到达顶点 j ， 但通过顶点k有 i -> k -> j 时 将更新i ，j 关系为可到达即
   d[ i ] [ j ] = max( d[ i ] [ j ] , d[ i ] [ k ] && d[ k ] [ j ] )
   

算法模板

memset(d, 0 ,sizeof d);
/*
输入数据 更新d[i][j]
*/
for(int k=1; k<=n; k++){
     for(int i=1; i<=n; i++){
         for(int j=1; j<=n; j++){
             d[i][j]=max(d[i][j], d[i][k]&&d[k][j]);
         }
     }
 }

例题

稍微复杂些的例题AcWing.343. 排序.
题目要求的是不等式的大小顺序， 和确定顺序的迭代次数 t （指从前往后进行加边，恰好确定大小顺序的边数）。 通过每次加边后求一次Floyd算法， 再依次判断任意两点间关系是否矛盾， 以及大小关系是否得到。

最小环问题

给定一张无向图，求图中一个至少包含 3个点的环，环上的节点不重复，并且环上的边的长度之和最小。该问题称为无向图的最小环问题。

求最小环权值

例题: 洛谷P6175.

给定一张无向图，求图中一个至少包含 3 个点的环，环上的节点不重复，并且环上的边的长度之和最小。该问题称为无向图的最小环问题。在本题中，你需要输出最小的环的边权和。

算法过程

通过以上的学习， 应该可以了解用Floyd求最短路， 那最小环如何求解呢?

在每次以顶点 k 为中间点求得完最短路后， 再循环更新任意两点间的最小回路即可啦。不过需要注意的是， 构成环的三个点必须不同， 在你枚举到的中点k时，前k-1个顶点的最短路径已经求出了且均不包含k， 在前k-1个点中枚举点对i， j 得到求出的最小环i - j， 如果k与二者均有连边， 便可以构成一个由 i - j - k - i的环。

需要用到最小环权值数组d[ ][ ]， 图中已知的权值数组a[ ][ ]。

1. 最小环权值数组与存图矩阵数组全部赋值为无穷大。设置一变量ans存储最小环的答案，初始值同样设为无穷大。
2. 依次枚举中间顶点k ， 依次枚举小于k的点对（i，j），如果k与二者均有连边， 更新答案
   ans = min(ans, d[ i ][ j ] + a[ i ][ k ] + a[ k ][ j ])
3. Floyd的算法来更新以顶点k为中间点的 小于等于n的顶点点对（i， j）的最小路径。

算法模板

memset(d, 0x3f ,sizeof d);
memset(a, 0x3f ,sizeof a);
int ans=0x3f3f3f3f;
/*
输入数据 矩阵存图中两点边权a[i][j]
*/
for(int k=1; k<=n; k++){
	for(int i=1; i<=n; i++){
        for(int j=1; j<=n; j++){
        	ans=min(ans, d[i][j]+a[i][k]+a[k][j]); 
   //将i-j的最短路/i-j/中连上点k构成 /i-j/-k-i的环
   //即答案 /i-j/的最短路径权值 加上 从 j到k的边权 与 从 i到k的边权
        }
    }
    for(int i=1; i<=n; i++){
        for(int j=1; j<=n; j++){
            d[i][j]=max(d[i][j], a[i][k]+a[k][j]);
            //更新i-j的最短路径
        }
     }
 }

求最小环路径

给定一张无向图，求图中一个至少包含 3 个点的环，环上的节点不重复，并且环上的边的长度之和最小。该问题称为无向图的最小环问题。你需要输出最小环的方案。

算法过程

最小环路径就是在求最小环的基础上再加上一个存储两点经过的中点数组pos[ ][ ] 比如pos[ i ][ j ]表示顶点 i - 顶点 j 的最短路径经过的中点是什么。再根据pos数组进行递归，便可以求得 从 i - j 的路径。

代码模板

ll d[105][105];
ll a[105][105];
int pos[105][105];
vector<int> path;
ll ans=0x3f3f3f3f;

void dfs(int i,int j){
    int k=pos[i][j];
    if(k==0) return;
    dfs(i, k);
    path.push_back(k);
    dfs(k,j);
}
void get_p(int i,int j,int k){
    path.clear();
    path.push_back(k);
    path.push_back(i);
    dfs(i, j);
    path.push_back(j);
}

void floyd(){
	for(int k=1; k<=n; k++){
        for(int i=1; i<k; i++)
            for(int j=i+1; j<k; j++)
                if(ans > (d[i][j]+a[i][k]+a[k][j]) ){
                    ans = (d[i][j]+a[i][k]+a[k][j]);
                    get_p(i,j,k);
                }
        for(int i=1; i<=n; i++)
            for(int j=1; j<=n; j++)
                if(d[i][j] > d[i][k]+d[k][j]){
                d[i][j] = d[i][k]+d[k][j];
                //d[j][i]=d[i][j];
                pos[i][j]=k;
            }
    }
    if(ans==inf)cout<<"No solution.";
    else
        for(auto x:path)
            cout << x << " ";
    cout << "\n";
}

例题

AcWing344观光之旅

求恰好经过k条边的最短路

给定一张由 T 条边构成的无向图，点的编号为 1∼1000 之间的整数。求从起点 S 到终点 E 恰好经过 N 条边（可以重复经过）的最短路。

emmmm不早了先睡了 有空再来填坑！