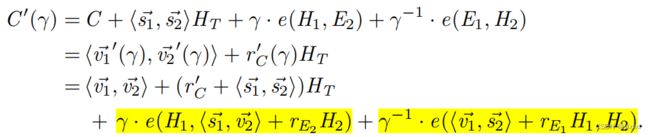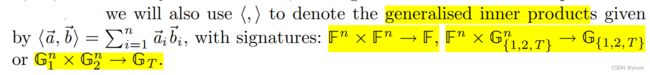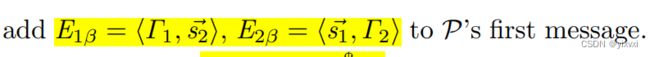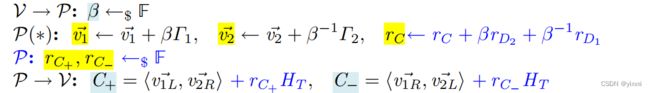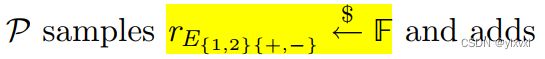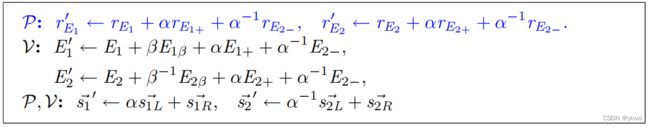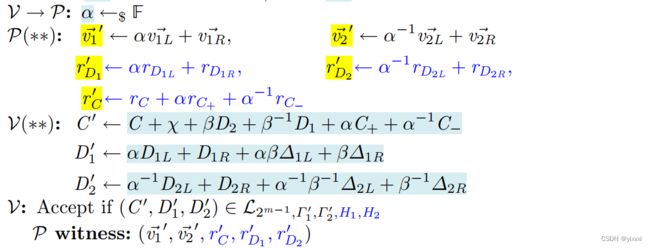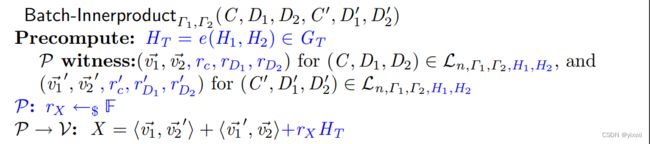论文笔记Dory:Arguments for Inner Products and Polynomial Commitments
Lee, J. (2021). Dory: Efficient, Transparent Arguments for Generalised Inner Products and Polynomial Commitments. TCC 2021
https://link.springer.com/chapter/10.1007/978-3-030-90453-1_1
DualDory中降低DualRing验证复杂度的主要工具是Dory内积证明方案
Dory, a transparent setup, public-coin interactive argument for inner-pairing products between committed vectors of elements of two source groups.
对于长度为 n n n的向量的积,证明是 6 l o g n 6 log~ n 6log n个目标群元素和 O ( 1 ) O(1) O(1)个附加元素。验证者的工作主要是目标组中的 O ( l o g n ) O(log ~n) O(log n)次幂和 O ( 1 ) O(1) O(1)对。安全性被归约为标准模型中的标准SXDH假设。
(以下是对内积关系的证明部分,不包括多项式承诺)
证明思路:首先定义包含内积的零知识关系语言(称为原始关系)
- 构造对标量积的证明
- 构造将关系的维度从 2 m 2^m 2m归约到 2 m − 1 2^{m-1} 2m−1的方法
- 对于一对群上的n维内积关系,先递归迭代归约方法直到关系中的内积缩成标量积,然后对标量积进行证明。关系的验证过程可延迟统一进行。
对于标量向量的内积证明:首先改进内积的零知识关系语言(称为改进关系)
- 从改进关系归约到原始关系语言的O(n)方法
- 改进维度归约方法
- 改进内积(递归归约)算法,将递归缩成标量积的改进关系归约到原始标量积关系,然后对原始标量积关系进行证明
Preliminaries
notations
Computationally Hard Problems in Type III Pairings
Pedersen 承诺

AFGHO承诺

Commitments to matrices:结合以上两种

V i = ⟨ Γ 1 , M i ⟩ + r r o w s , i H 1 ∈ G 1 , V ⃗ ∈ G 1 n V_i=\langle\Gamma_1,M_i\rangle+r_{rows,i}H_1\in\mathbb{G}_1,\vec{V}\in\mathbb{G}_1^n Vi=⟨Γ1,Mi⟩+rrows,iH1∈G1,V∈G1n
C = ( ⟨ Γ 2 , V ⃗ ⟩ + r f i n ⋅ H T , r f i n ) ∈ G T C=(\langle\Gamma_2,\vec{V}\rangle+r_{fin}\cdot H_T,r_{fin})\in\mathbb{G}_T C=(⟨Γ2,V⟩+rfin⋅HT,rfin)∈GT
打开:
r i g h t = ∑ i Γ 2 i V i + r f i n ⋅ H T = C = l e f t right=\sum_i \Gamma_{2i} V_i+r_{fin}\cdot H_T=C=left right=∑iΓ2iVi+rfin⋅HT=C=left
An Inner-Product Argument with a Logarithmic Verifier
两个向量的内积argument: v ⃗ 1 ∈ G 1 n , v ⃗ 2 ∈ G 2 n \vec{v}_1\in\mathbb{G}_1^n,\vec{v}_2\in\mathbb{G}_2^n v1∈G1n,v2∈G2n,用 AFGHO commitments 生成承诺(生成元为 ( Γ 2 , e ( H 1 , H 2 ) ) ∈ G 2 n × G T , ( Γ 1 , e ( H 1 , H 2 ) ) ∈ G 1 n × G T (\Gamma_2,e(H_1,H_2))\in\mathbb{G}_2^n\times\mathbb{G}_T,(\Gamma_1,e(H_1,H_2))\in\mathbb{G}_1^n\times\mathbb{G}_T (Γ2,e(H1,H2))∈G2n×GT,(Γ1,e(H1,H2))∈G1n×GT)

Scalar-Product
从低维开始, L 1 , Γ 1 , Γ 2 , H 1 , H 2 \mathcal{L}_{1,\Gamma_1,\Gamma_2,H_1,H_2} L1,Γ1,Γ2,H1,H2,向量变成了标量 v 1 ∈ G 1 , v 2 ∈ G 2 v_1\in\mathbb{G}_1,v_2\in\mathbb{G}_2 v1∈G1,v2∈G2,在 AFGHO承诺下的标量积(类比的在Pedersen承诺下的argument是传说???)。
由于配对比 G 1 \mathbb{G}_1 G1或 G 2 \mathbb{G}_2 G2中的乘法更昂贵,因此我们将通常的最后三次检查合并为具有验证者挑战的单个配对

目标是零知识证明两个标量 v 1 , v 2 v_1,v_2 v1,v2的内积,且不泄露标量
l e f t = e ( E 1 , E 2 ) + e ( Γ 1 , Γ 2 ) + e ( E 1 , d − 1 Γ 2 ) + e ( d Γ 1 , E 2 ) = [ e ( d 1 , d 2 ) + e ( c v 1 , c v 2 ) + e ( d 1 , c v 2 ) + e ( c v 1 , d 2 ) ] + [ e ( Γ 1 , Γ 2 ) ] + [ e ( d 1 , d − 1 Γ 2 ) + e ( c v 1 , d − 1 Γ 2 ) ] + [ e ( d Γ 1 , d 2 ) + e ( d Γ 1 , c v 2 ) ] = [ ( R − r R H T ) + ( c 2 C − c 2 r C H T ) + ( c Q − c r Q H T ) ] + [ X ] + [ ( d − 1 P 1 − d − 1 r P 1 H T ) + ( c d − 1 D 1 − c d − 1 r D 1 H T ) + ( d P 2 − d r P 2 H T ) + ( c d D 2 − c d r D 2 H T ) ] = r i g h t \begin{aligned} left &= e(E_1,E_2)+e(\Gamma_1,\Gamma_2)+e(E_1,d^{-1}\Gamma_2)+e(d\Gamma_1,E_2) \\ &=[e(d_1,d_2)+e(cv_1,cv_2)+e(d_1,cv_2)+e(cv_1,d_2)]+[e(\Gamma_1,\Gamma_2)]\\ &+[e(d_1,d^{-1}\Gamma_2)+e(cv_1,d^{-1}\Gamma_2)]+[e(d\Gamma_1,d_2)+e(d\Gamma_1,cv_2)]\\ &=[(R-r_RH_T)+(c^2C-c^2r_CH_T)+(cQ-cr_QH_T)]+[\mathcal{X}]\\ &+[(d^{-1}P_1-d^{-1}r_{P_1}H_T)+(cd^{-1}D_1-cd^{-1}r_{D_1}H_T)+(dP_2-dr_{P_2}H_T)+(cdD_2-cdr_{D_2}H_T)]\\ &=right \end{aligned} left=e(E1,E2)+e(Γ1,Γ2)+e(E1,d−1Γ2)+e(dΓ1,E2)=[e(d1,d2)+e(cv1,cv2)+e(d1,cv2)+e(cv1,d2)]+[e(Γ1,Γ2)]+[e(d1,d−1Γ2)+e(cv1,d−1Γ2)]+[e(dΓ1,d2)+e(dΓ1,cv2)]=[(R−rRHT)+(c2C−c2rCHT)+(cQ−crQHT)]+[X]+[(d−1P1−d−1rP1HT)+(cd−1D1−cd−1rD1HT)+(dP2−drP2HT)+(cdD2−cdrD2HT)]=right
Dory-Reduce
LCC-DLOG
Dory建立在LCC-DLOG传统的基础上,构造内积证明或Hadamard积到内积的归约,通过同态承诺的有效证明和次线性通信。
显式地将内积表示为双线性形式,这些为标量向量和群元素之间的内积证明,或配对源群之间的广义积提供了参数,其中任何一个输入都可能被承诺。
令向量的长度为 n ′ n' n′,是2的幂。对于任何向量和非零标量 a a a:
![]()
关于长度 n ′ n' n′的内积 ⟨ u ⃗ , v ⃗ ⟩ \langle\vec u,\vec v\rangle ⟨u,v⟩能被规约为长度为 n ′ / 2 n'/2 n′/2的向量内积。验证者利用承诺方案(不失一般性为 u ⃗ \vec u u)的同态属性以及一些证明者的帮助找到对这些短向量 u ⃗ ′ = a u L ⃗ + u R , v ⃗ ′ = a − 1 v L ⃗ + v R ⃗ \vec u'=a\vec{u_L}+{u_R},\vec v'=a^{-1}\vec{v_L}+\vec{v_R} u′=auL+uR,v′=a−1vL+vR的承诺,以及对内积 ⟨ u ⃗ ′ , v ⃗ ′ ⟩ \langle\vec u',\vec v'\rangle ⟨u′,v′⟩的承诺的声明,对于一些验证者的挑战 a a a。此程序递归地应用于获得关于长度为1的向量的声明,其中使用了一些sigma协议。计算的可靠性来自于对证明程序的倒带,因为 u ⃗ \vec u u可以从作为 a a a的函数的几个 u ⃗ ′ \vec u' u′的样本中恢复出来。
Dory-Reduce
一个交互式论证,从成员关系 L 2 m , Γ 1 , Γ 2 , H 1 , H 2 \mathcal{L}_{2^m,\Gamma_1,\Gamma_2,H_1,H_2} L2m,Γ1,Γ2,H1,H2归约到成员关系 L 2 m − 1 , Γ 1 ′ , Γ 2 ′ , H 1 , H 2 \mathcal{L}_{2^{m-1},\Gamma_1',\Gamma_2',H_1,H_2} L2m−1,Γ1′,Γ2′,H1,H2
设:
![]()
采用类似于LCC-DLOG,用 V \mathcal{V} V挑战 α \alpha α将每个压缩成大约 2 m − 1 2^{m-1} 2m−1长度的向量 v i α ′ ⃗ , Γ i α \vec{v_{i\alpha}'},\Gamma_{i\alpha} viα′,Γiα:
![]()
P , V \mathcal{P,V} P,V会分别用 α \alpha α和预先计算的数据来计算承诺 Δ 1 = ⟨ v 1 α ⃗ , Γ 2 ′ ⟩ , Δ 2 = ⟨ Γ 1 ′ , v 2 α ⃗ ⟩ \Delta_1=\langle\vec{v_{1\alpha}},\Gamma_2'\rangle,\Delta_2=\langle\Gamma_1',\vec{v_{2\alpha}}\rangle Δ1=⟨v1α,Γ2′⟩,Δ2=⟨Γ1′,v2α⟩。然后我们会根据额外的验证者挑战组合每个 i i i的 v i α ⃗ \vec{v_{i\alpha}} viα和 Γ i α \Gamma_{i\alpha} Γiα。最终从 C ′ , D 1 ′ , D 2 ′ C',D_1',D_2' C′,D1′,D2′产生了 C ′ ′ C'' C′′,从 D 1 ′ , Δ 1 D_1',\Delta_1 D1′,Δ1产生了 D 1 ′ ′ D_1'' D1′′,从 D 2 ′ , Δ 2 D_2',\Delta_2 D2′,Δ2产生了 D 2 ′ ′ D_2'' D2′′,证明方发送额外的交叉术语来支持这些组合。
然而,这种方法需要发送至少8个 G T \mathbb{G}_T GT元素(每个声明折叠两个,最后组合阶段两个)。相反,在Dory-Reduce中,我们有效地交换了这两个阶段的顺序,这允许只发送6个 G T \mathbb{G}_T GT元素。

预处理( P , V \mathcal{P,V} P,V共知): H T , Δ 1 L , Δ 1 R , Δ 2 L , Δ 2 R , X H_T,\Delta_{1L},\Delta_{1R},\Delta_{2L},\Delta_{2R},\mathcal{X} HT,Δ1L,Δ1R,Δ2L,Δ2R,X
第一轮sigma:
- P用公共值拆分计算向量 v 1 ⃗ , v 2 ⃗ \vec{v_1},\vec{v_2} v1,v2的左右部分的承诺AFGHO承诺发给V
- V返回挑战 β \beta β
(这一轮P拆分秘密值并提交承诺发给V,这些承诺是用于最后进行验证的;挑战 β \beta β在第二轮用于扰动以实现ZKP)
第二轮: - P用挑战值更新 v ⃗ 1 , v ⃗ 2 , r C \vec v_1,\vec v_2,r_C v1,v2,rC,将随机 r C + , r C − r_{C_+},r_{C_{-}} rC+,rC−发给V
- V返回挑战 α \alpha α
- P用挑战值更新所有的witness,同时V可以生成新的压缩语言 C ′ , D 1 ′ , D 2 ′ C',D_1',D_2' C′,D1′,D2′
l e f t = ⟨ v 1 ′ ⃗ , v 2 ′ ⃗ ⟩ + r C ′ H T = ⟨ v 1 L ⃗ , v 2 L ⃗ ⟩ + ⟨ v 1 R ⃗ , v 2 R ⃗ ⟩ + ⟨ v 1 L ⃗ , v 2 R ⃗ ⟩ α + ⟨ v 1 R ⃗ , v 2 L ⃗ ⟩ α − 1 + ( r C + α r C + + α − 1 r C − ) H T = ⟨ v 1 ⃗ , v 2 ⃗ ⟩ + α ( C + − r C + H T ) + α − 1 ( C − − r C − H T ) + ( r C H T + α r C + H T + α − 1 r C − H T ) = ⟨ v 1 ⃗ , v 2 ⃗ ⟩ + α C + + α − 1 C − + r C H T = ( ⟨ v 1 ⃗ , v 2 ⃗ ⟩ + ⟨ Γ 1 , Γ 2 ⟩ + ⟨ Γ 1 , v 2 ⃗ ⟩ β − 1 + ⟨ v 1 ⃗ , Γ 2 ⟩ β ) + α C + + α − 1 C − + ( r C H T + β r D 2 H T + β − 1 r D 1 H T ) = r i g h t \begin{aligned} left &= \langle \vec{v_1'},\vec{v_2'}\rangle+r_C'H_T=\langle\vec{v_{1L}},\vec{v_{2L}}\rangle+\langle\vec{v_{1R}},\vec{v_{2R}}\rangle+\langle\vec{v_{1L}},\vec{v_{2R}}\rangle^\alpha+\langle\vec{v_{1R}},\vec{v_{2L}}\rangle^{\alpha^{-1}}\\ &+(r_C+\alpha r_{C_+}+\alpha^{-1} r_{C_{-}})H_T\\ &=\langle \vec{v_1},\vec{v_2}\rangle+\alpha(C_{+}-r_{C_{+}}H_T)+\alpha^{-1}(C_{-}-r_{C_{-}}H_T)\\ &+(r_CH_T+\alpha r_{C_+}H_T+\alpha^{-1} r_{C_{-}}H_T)\\ &=\langle \vec{v_1},\vec{v_2}\rangle+\alpha C_{+}+\alpha^{-1}C_{-}+r_CH_T\\ &= (\langle \vec{v_1},\vec{v_2}\rangle+\langle\Gamma_1,\Gamma_2\rangle+\langle\Gamma_1,\vec{v_2}\rangle^{\beta^{-1}}+\langle\vec{v_1},\Gamma_2\rangle^{\beta})+\alpha C_{+}+\alpha^{-1}C_{-}\\ &+(r_CH_T+\beta r_{D_2}H_T+\beta^{-1} r_{D_{1}}H_T)\\ &=right \end{aligned} left=⟨v1′,v2′⟩+rC′HT=⟨v1L,v2L⟩+⟨v1R,v2R⟩+⟨v1L,v2R⟩α+⟨v1R,v2L⟩α−1+(rC+αrC++α−1rC−)HT=⟨v1,v2⟩+α(C+−rC+HT)+α−1(C−−rC−HT)+(rCHT+αrC+HT+α−1rC−HT)=⟨v1,v2⟩+αC++α−1C−+rCHT=(⟨v1,v2⟩+⟨Γ1,Γ2⟩+⟨Γ1,v2⟩β−1+⟨v1,Γ2⟩β)+αC++α−1C−+(rCHT+βrD2HT+β−1rD1HT)=right
Dory-Innerproduct
Precompute构造每一次迭代所需要的公共值,然后进行总共m次迭代将最初的关于语言 C , D 1 , D 2 C,D_1,D_2 C,D1,D2归约到乘积。然后应用Scalar-Product。

延迟验证
延迟对Dory-Reduce中的关系进行验证,直到所有迭代完成。


以最小的两个为例:
C = C m − 1 + X m − 1 + β m − 1 ( D 2 m − 1 ) + β − 1 ( D 1 m − 1 ) + α m − 1 C + m − 1 + α m − 1 − 1 C − m − 1 = ( C m − 2 + X m − 2 + β m − 2 ( D 2 m − 2 ) + β − 1 ( D 1 m − 2 ) + α m − 2 C + m − 2 + α m − 2 − 1 C − m − 2 ) + X m − 1 + β m − 1 ( D 2 m − 1 ) + β m − 1 − 1 ( D 1 m − 1 ) + α m − 1 C + , m − 1 + α m − 1 − 1 C − , m − 1 = C m − 2 + ∑ i = m − 1 m − 2 X i + β m − 2 ( D 2 m − 2 ) + β − 1 ( D 1 m − 2 ) + ∑ j = m − 1 m − 2 ( α j C + j + α j − 1 C − j ) + β m − 1 ( α m − 2 − 1 ( D 2 L m − 2 ) + ( D 2 R m − 2 ) + α m − 2 − 1 β m − 2 − 1 ( Δ 2 L m − 2 ) + β m − 2 − 1 ( Δ 2 R m − 2 ) ) + β m − 1 − 1 ( α m − 2 ( D 1 L m − 2 ) + ( D 1 R m − 2 ) + α m − 2 β m − 2 ( Δ 1 L m − 2 ) + β m − 2 ( Δ 1 R m − 2 ) ) \begin{aligned} C&=C_{m-1}+\mathcal{X}_{m-1}+\beta_{m-1}(D_{2}^{m-1})+\beta^{-1}(D_{1}^{m-1})+\alpha_{m-1}C_{+}^{m-1}+\alpha_{m-1}^{-1}C_{-}^{m-1}\\ &=(C_{m-2}+\mathcal{X}_{m-2}+\beta_{m-2}(D_{2}^{m-2})+\beta^{-1}(D_{1}^{m-2})+\alpha_{m-2}C_{+}^{m-2}+\alpha_{m-2}^{-1}C_{-}^{m-2})\\ &+\mathcal{X}_{m-1}+\beta_{m-1}(D_{2}^{m-1})+\beta_{m-1}^{-1}(D_{1}^{m-1})+\alpha_{m-1}C_{+,m-1}+\alpha_{m-1}^{-1}C_{-,m-1}\\ &=C_{m-2}+\sum_{i=m-1}^{m-2}\mathcal{X}_i+\beta_{m-2}(D_{2}^{m-2})+\beta^{-1}(D_{1}^{m-2})+\sum_{j=m-1}^{m-2}(\alpha_{j}C_{+}^j+\alpha_{j}^{-1}C_{-}^j)\\ &+\beta_{m-1}(\alpha_{m-2}^{-1}(D_{2L}^{m-2})+(D_{2R}^{m-2})+\alpha_{m-2}^{-1}\beta_{m-2}^{-1}(\Delta_{2L}^{m-2})+\beta_{m-2}^{-1}(\Delta_{2R}^{m-2}))\\ &+\beta_{m-1}^{-1}(\alpha_{m-2}(D_{1L}^{m-2})+(D_{1R}^{m-2})+\alpha_{m-2}\beta_{m-2}(\Delta_{1L}^{m-2})+\beta_{m-2}(\Delta_{1R}^{m-2}))\\ \end{aligned} C=Cm−1+Xm−1+βm−1(D2m−1)+β−1(D1m−1)+αm−1C+m−1+αm−1−1C−m−1=(Cm−2+Xm−2+βm−2(D2m−2)+β−1(D1m−2)+αm−2C+m−2+αm−2−1C−m−2)+Xm−1+βm−1(D2m−1)+βm−1−1(D1m−1)+αm−1C+,m−1+αm−1−1C−,m−1=Cm−2+i=m−1∑m−2Xi+βm−2(D2m−2)+β−1(D1m−2)+j=m−1∑m−2(αjC+j+αj−1C−j)+βm−1(αm−2−1(D2Lm−2)+(D2Rm−2)+αm−2−1βm−2−1(Δ2Lm−2)+βm−2−1(Δ2Rm−2))+βm−1−1(αm−2(D1Lm−2)+(D1Rm−2)+αm−2βm−2(Δ1Lm−2)+βm−2(Δ1Rm−2))
故而推理成立。
Batching Inner Products
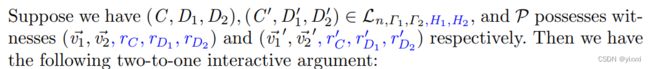

C ∗ = ⟨ v 1 ⃗ ′ ′ , v 2 ⃗ ′ ′ ⟩ + r C ′ ′ H T = ⟨ v 1 ⃗ , v 2 ⃗ ⟩ γ 2 + ⟨ v 1 ⃗ ′ , v 2 ⃗ ′ ⟩ + ⟨ v 1 ⃗ , v 2 ⃗ ′ ⟩ γ + ⟨ v 1 ⃗ ′ , v 2 ⃗ ⟩ γ + ( γ 2 r C + γ r X + r C ′ ) H T = γ 2 C + C ′ + γ X = C ′ ′ D 1 ∗ = ⟨ v 1 ⃗ ′ ′ , Γ 2 ⟩ + r D 1 ′ ′ H T = ⟨ v 1 ⃗ , Γ 2 ⟩ γ + ⟨ v 1 ⃗ ′ , Γ 2 ⟩ + γ r D 1 + r D 1 ′ = γ D 1 + D 1 ′ = D 1 ′ ′ D 2 ∗ = ⟨ Γ 1 , v 2 ⃗ ′ ′ ⟩ + r D 2 ′ ′ H T = ⟨ Γ 1 , v 2 ⃗ ⟩ γ + ⟨ Γ 1 , v 2 ⃗ ′ ⟩ + γ r D 2 + r D 2 ′ = γ D 2 + D 2 ′ = D 2 ′ ′ \begin{aligned} C^*&=\langle\vec{v_1}'',\vec{v_2}''\rangle+r_C''H_T\\ &=\langle\vec{v_1},\vec{v_2}\rangle^{\gamma^2}+\langle\vec{v_1}',\vec{v_2}'\rangle+\langle\vec{v_1},\vec{v_2}'\rangle^{\gamma}+\langle\vec{v_1}',\vec{v_2}\rangle^{\gamma}+(\gamma^2r_C+\gamma r_X+r_C')H_T\\ &=\gamma^2C+C'+\gamma X=C''\\ D_1^*&=\langle\vec{v_1}'',\Gamma_2\rangle+r_{D_1}''H_T\\ &=\langle\vec{v_1},\Gamma_2\rangle^{\gamma}+\langle\vec{v_1}',\Gamma_2\rangle+\gamma r_{D_1}+r_{D_1}'\\ &=\gamma D_1+D_1'=D_1''\\ D_2^*&=\langle\Gamma_1,\vec{v_2}''\rangle+r_{D_2}''H_T\\ &=\langle\Gamma_1,\vec{v_2}\rangle^{\gamma}+\langle\Gamma_1,\vec{v_2}'\rangle+\gamma r_{D_2}+r_{D_2}'\\ &=\gamma D_2+D_2'=D_2''\\ \end{aligned} C∗D1∗D2∗=⟨v1′′,v2′′⟩+rC′′HT=⟨v1,v2⟩γ2+⟨v1′,v2′⟩+⟨v1,v2′⟩γ+⟨v1′,v2⟩γ+(γ2rC+γrX+rC′)HT=γ2C+C′+γX=C′′=⟨v1′′,Γ2⟩+rD1′′HT=⟨v1,Γ2⟩γ+⟨v1′,Γ2⟩+γrD1+rD1′=γD1+D1′=D1′′=⟨Γ1,v2′′⟩+rD2′′HT=⟨Γ1,v2⟩γ+⟨Γ1,v2′⟩+γrD2+rD2′=γD2+D2′=D2′′
Inner Products with Public Vectors of Scalars
在上一节中构造了Dory-Innerproduct,这是 G 1 n \mathbb G_1^n G1n和 G 2 n \mathbb G_2^n G2n中承诺向量之间广义内积的一个简明的知识论证.
对于多项式承诺格式,还要求能够证明承诺向量的乘积,其中向量是具有乘法结构的标量向量。
然而,当实例被批处理时,这个结构不会被保留,因此我们将扩展我们的参数,以允许 F n \mathbb F_n Fn中的一般向量.
一组向量 s 1 ⃗ , s 2 ⃗ ∈ F n \vec{s_1},\vec{s_2}\in\mathbb F_n s1,s2∈Fn,定义语言:

General Reduction with O(n) cost
从 L n , Γ 1 , Γ 2 , H 1 , H 2 ( s 1 ⃗ , s 2 ⃗ ) \mathcal L_{n,\Gamma_1,\Gamma_2,H_1,H_2}(\vec{s_1},\vec{s_2}) Ln,Γ1,Γ2,H1,H2(s1,s2)归约到 L n , Γ 1 , Γ 2 , H 1 , H 2 \mathcal L_{n,\Gamma_1,\Gamma_2,H_1,H_2} Ln,Γ1,Γ2,H1,H2,证明者验证者的代价是 O ( n ) \mathcal O(n) O(n),其中 s i ⃗ \vec{s_i} si基本上乘以 G i \mathbb G_i Gi中V选择的挑战,并添加到见证向量中。