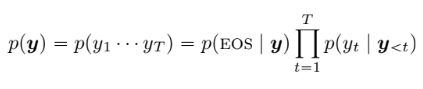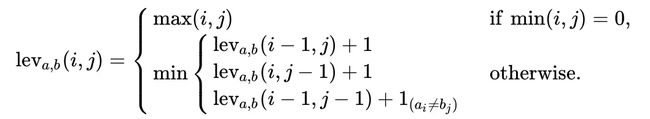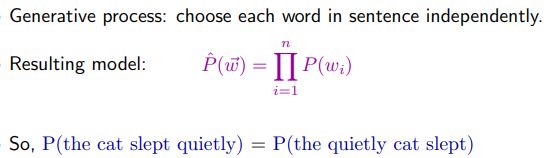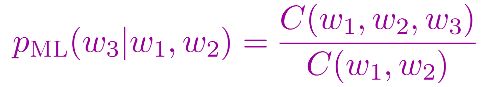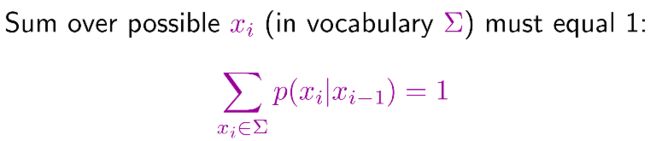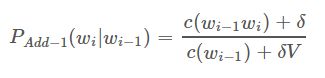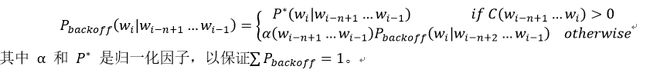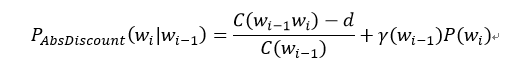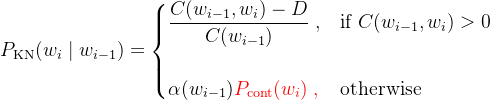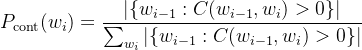NLP入门——语言结构/语言建模
一、Linguistics 语言学
- words
- morphology 形态学：词的构成和内部结构研究。如英语的dog、dogs和dog-catcher有相当的关系
- morpheme 语素：最小的语法单位，是最小的音义结合体
- lexeme 词位：词的意义的基本抽象单位，是一组通过形态变化相联系的词的集合。例如 run、runs、ran 和 running 都属于同一个词位，可标识为 RUN。词位也是词法学分析中，指代相同词根(stems)、不同形式的一组词的单位。词性不同词位会不同。
- lemma 词目：词位按惯例确认的典型形式。例如词位 RUN 的词目是 run。词目是词典的基本查检单位和解释对象，位于词条首位，不规则的形态变化、不常见的其他形式常在词条以下列出。不过，有的语言学字典视两者为同样的概念。
- lexicon：词库，所有词汇
- parts of speech（POS） 词类：
- Open classes ○ nouns ○ verbs ○ adjectives ○ adverbs
- Closed classes ○ prepositions 介词○ determiners 限定词○ pronouns 代词 ○ conjunctions 连词 ○ auxiliary verbs 助动词
- syntax 句法：句子的构成和内部结构的研究
- semantics 语义：句子意义的研究
- discourse 语篇：理解文档中的句子之间是如何关联起来的。因此，当我们浏览一个文档时，语篇为我们提供了一个关于该文档的连贯的故事线
- Phonetics语音学：人类语言声音的研究
- Phonology音韵学：人类语言中声音系统的研究
- Pragmatics语用学：研究具有语义意义的句子用于特定交际目标的方式
1. 语素 morphemes
词素是最小的有意义的语言单位，不能够进一步划分为更小的单位而不破话或彻底改变其词汇意义或语法意义。
语素和词的区别在于，许多语素不能独立存在。而能够单独存在并且有意义的语素叫做词根（Stems）；不能独立存在，要借助其他语素表达意义的语素则称之为词缀 （affixes）。每个词都包含最少一个语素。按能否独立成词对语素分类：
- 自由语素（Free morphemes）：可以独立成词，如cat，town
- 规范语素（Bound morphemes）：必须和词根或者其他规范语素一起成词，如-tion，-ing, -s
所有的规范语素（Bound morphemes）都是词缀 （affixes），从功能上也可分为派生词缀和屈折词缀。位于词根前的词缀，叫做前缀（prefix），跟在词根后面的词缀，叫做后缀（suffix），如果插入在词干中间的，叫做中缀（infix）
规范语素可以进一步分类，分为：
- 派生语素 ( Derivational morpheme)：可以和其他语素结合成为一个新的词，带来新的语义。如英语中的派生后缀-ly，使形容词slow变为副词slowly。前缀un-在一些形容词和动词前面表示否定的意义，如unhealthy
- 屈折语素 ( Inflectional morpheme )：通常改变词的语法范畴，而不改变词义。屈折语素改变动词的时、体、式、态等范畴，改变名词、代词、形容词的格、数和性等范畴。比如说英语的动词加-s表示第三人称单数，但不改变其动词属性
需要特别指出，有时候派生语素和屈折语素会采用同一种表现形式。比如说，-er，当这个后缀跟在形容词后面，它作为屈折语素，表示比较级；当跟在动词后面，则是一个派生语素，形成一个新词，如cook-cooker。
从意义的虚实来说，语素又可分为：
- 内容语素（Content morpheme）：携带具体的语义，如cat，-able和-un。内容语素包括名词、动词、副词、形容词，也包括规范语素中的派生语素（Derivational morpheme）
- 功能语素（Function morpheme）：仅仅提供语法信息或句法一致，如and， plural-s。包括介词、连词、代词，和限定词，以及规范语素中的屈折语素（Inflectional morpheme）
2. 形态学 Morphology
词的分类
- variable and invariable words 变化词：实义词 非变化词：语法词
- Lexical words and grammatical words 实义词和语法词
- Open class and closed class 开放类词：实义词 封闭类词：语法词
3. Laws of text 语言统计学三大定律
- Zipf’s Law：在给定的语料中，对于任意一个term，其频度(freq)的排名（rank）和freq的乘积大致是一个常数
- Benford’s Law：在自然形成的十进制数据中，任何一个数据的第一个数字d出现的概率大致log10(1+1/d)
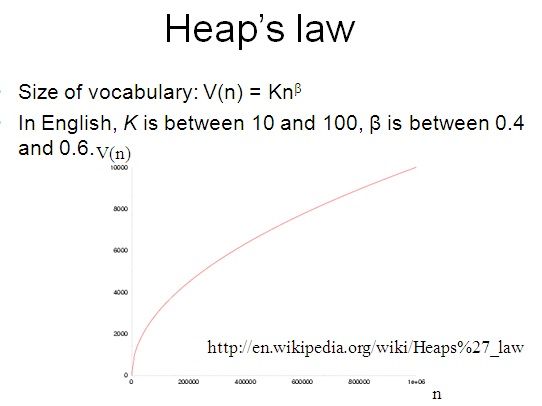
- Heap’s Law：在给定的语料中，其独立的term数（vocabulary的size）v（n）大致是语料大小（n）的一个指数函数
3.1. Zipf’s Law 齐夫定律
齐夫定律是一个实验定律。在自然语言的语料库里，一个单词出现的频率与它在频率表里的排名成反比。所以，频率最高的单词出现的频率大约是出现频率第二位的单词的2倍，而出现频率第二位的单词则是出现频率第四位的单词的2倍。
给出一组齐夫分布的频率，按照从最常见到非常见排列，第二常见的频率是最常见频率的出现次数的½，第三常见的频率是最常见的频率的1/3，第n常见的频率是最常见频率出现次数的1/n。然而，这并不精确，因为所有的项必须出现一个整数次数，一个单词不可能出现2.5次。
3.2. Benford’s Law 本福特定律
Benford's law 描述了真实数字数据集中首位数字的频率分布。一堆从实际生活得出的数据中，以1为首位数字的数的出现概率约为总数的三成，接近直觉得出之期望值1/9的3倍。推广来说，越大的数，以它为首几位的数出现的概率就越低。它可用于检查各种数据是否有造假。但要注意使用条件：1.数据之间的差距应该足够大。2.不能有人为操控。
本福特定律说明在b进位制中，以数n起头的数出现的概率为
其中，n=1,2,...,b-1
本福特定律(Benford's law)的直观解释 - 知乎
3.3 Heap’s Law
Heaps定律将词项的数目估计成文档集大小的一个函数
，其中n是文档集合中的词条个数。参数k和b的典型取值为30<=k<=100, β≈0.5
Heaps定律认为，文档集大小和词汇量之间可能存在的就最简单的关系是它们在对数空间（log-log space）中存在线性关系.
不同的文档集下参数k的取值差异会比较大，这是因为词汇量的大小依赖于文档集本身以及对它进行处理的方法。
- 大小写转换和词干还原会降低词汇量的增长率
- 允许加入数字和容忍拼写错误会增加该增长率
不论在某个特定的文档集中的参数取值如何，Heaps定律提出了如下两点假设：
- (1)随着文档数目的增加，词汇量会持续增长而不会稳定到一个最大值；
- (2)大规模文档集的词汇量也会非常大。
因此在大规模文档集情况下，词典压缩对于建立一个有效的信息检索系统来说是非常重要的。
二、语言建模
1. 概率建模原则
- 句子概率作为衡量句子是否符合语法的标准是没有用的（sentence probability is useless as a measure of whether a sentence is grammatical）
- 语言概率建模：自回归因子分解（两个问题：不是所有条件概率都有效；无限序列时概率会丢失）
2. Language Models
2.1 formal language theorys
例如：
2.2 language models
即一个简单的语言模型应至少满足概率和为一：
3. 词性标注（POS tagging )
3.1 介绍
- Parts-of-speech(也称为词性、词类或句法类别)很有用，因为它们揭示了一个单词及其相邻词的很多信息。知道一个单词是名词还是动词可以告诉我们可能的相邻单词(名词前面有限定词和形容词，动词前面有名词)和句法结构单词(名词通常是名词短语的一部分)，使词性标注成为解析的一个关键方面。
- 词性标注是为输入文本中的每个词性标注词分配词性标记的过程。标记算法的输入是一系列(标记化的)单词和标记集，输出是一系列标记，每个标记一个。
- 词性标注的两种算法——词性赋值算法。一种是生成隐马尔可夫模型(HMM)，另一种是判别最大熵马尔可夫模型(MEMM)
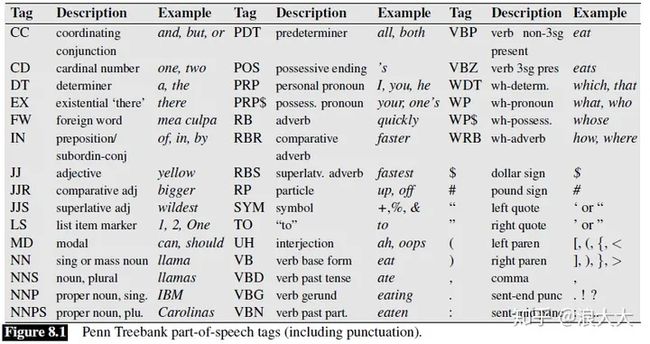
一些tagsets
- Penn Treebank 45 tags
- Brown corpus 87 tags
- C7 tagset 146 tags
3.2 Criteria for classifying words
- Distributional criteria: Where can the words occur? 上下文位置
- Morphological criteria: What form does the word have? (E.g. -tion, -ize). What affixes can it take? (E.g. -s, -ing, -est). 单词的形态
- Notional (or semantic) criteria: What sort of concept does the word refer to? (E.g. nouns often refer to ‘people, places or things’). More problematic: less useful for us. 具体词汇代指的含义
3.3 Open and closed classes 自然语言的封闭词类和开放词类
- Open classes are typically large, have fluid membership, and are often stable under translation. Four major open classes are widely found in languages worldwide: nouns, verbs, adjectives, adverbs. 所有语言至少有前两种类型（名词和动词）
- Closed classes are typically small, have relatively fixed membership, and the repertoire of classes varies widely between languages. E.g. prepositions (English, German), post-positions (Hungarian, Urdu, Korean), particles (Japanese), classifiers (Chinese), etc.
- Closed-class words (e.g. of, which, could) often play a structural role in the grammar as function words.
一些closed class words：
- prepositions: on, under, over, near, by, at, from, to, with
- determiners: a, an, the
- conjunctions: and, but, or, as, if, when
- particles: up, down, on, off, in, out, at, by
- numerals: one, two, three, first, second, third
3.4 Types of lexical ambiguity 词性不确定
Part of Speech (PoS) Ambiguity: e.g., still:
- adverb: at present, as yet
- noun: (1) silence; (2) individual frame from a film; (3) vessel for distilling alcohol
- adjective: motionless, quiet
- transitive verb: to calm
Sense Ambiguity: e.g., bark:
- sound a dog makes (The dog’s bark woke me up in the morning)
- outer covering of a tree (The tree’s bark was rough to the touch)
3.5 Rule-based tagging 基于规则的标注
Very old POS taggers used to work in two stages, based on hand-written rules: the first stage identifies a set of possible POS for each word in the sentence (based on a lexicon), and the second uses a set of hand-crafted rules in order to select a POS from each of the lists for each word. Example
- If a word belongs to the set of determiners, tag is at DT.
- Tag a word next to a determiner as an adjective (JJ), if it ends with -ed.
- If a word appears after “is” or “are” and it ends with ing, tag it as a verb VBG.
3.6 Type-ambiguity versus token-ambiguity
Let 
be a corpus of words taken from W and 
their parts of speech. Let 
.
Calculating type-ambiguity: the size of the set Wambg divided by the size of W .
Calculating token-ambiguity: the size of the set 
divided by n.
The bottom line: The type-ambiguous words are the more frequent words!
3.7 tagging tasks (sequence labelling)
- Case restoration: If we just get lowercased text, we may want to restore proper casing, e.g. the river Thames
- Named entity recognition: it may also be useful to find names of persons, organizations, etc. in the text, e.g. Barack Obama
- Information field segmentation: Given specific type of text (classified advert, bibiography entry), identify which words belong to which “fields” (price/size/#bedrooms, author/title/year)
- Prosodic marking 韵律标记: In speech synthesis, which words/syllables have stress/intonation changes, e.g. He’s going. vs He’s going?
3.8 Universal POS tags
NOUN (nouns)
VERB (verbs)
ADJ (adjectives)
ADV (adverbs)
PRON (pronouns)
DET (determiners and articles)
ADP (prepositions and postpositions)
NUM (numerals)
CONJ (conjunctions)
PRT (particles)
’.’ (punctuation marks)
X (anything else, such as abbreviations or foreign words)
3.9 A probabilistic model for tagging
Let’s define a new generative process for sentences. To generate sentence of length n:
Let t0 =
For i = 1 to n
Choose a tag conditioned on previous tag: P(ti |ti−1)
Choose a word conditioned on its tag: P(wi |ti)
模型假设：
- Each tag depends only on previous tag: a bigram model over tags.
- Words are conditionally independent given tags
Arrows indicate probabilistic dependencies
使用 Probabilistic finite-state machine 有限机模型
- Prob of moving from state s to s′ (transition probability): P(ti = s′ |ti−1 = s)
- Prob of emitting w from state s (emission probability): P(wi = w|ti = s)
Let S = w1 . . .wn be the sentence and T = t1 . . .tn be the corresponding tag sequence. Then：
举例子：
对句子 This/DT is/VB a/DT simple/JJ sentence/NN 来说：
3.10 HMM(隐马尔科夫)词性标注
在本节中，我们将介绍隐马尔可夫模型在词性标注中的应用。HMM是一个序列模型。序列模型或序列分类器是一个模型，其工作是为序列中的每个单元分配一个标签或类，从而将一个观察序列(观察状态)映射到一个标签序列(隐藏状态)。HMM是一种概率序列模型：给定一个单位序列(单词、字母、语素、句子等等)，它计算可能的标签序列的概率分布，并选择最佳标签序列。
• Evaluation: Given a sentence S, calculate P(S) (“summing out” T) • Decoding: Given a sentence S, calculate arg maxT P(T | S). • Learning: Given a set of sentences S (1) , S (2) , ..., find the HMM that maximizes their log-likelihood
三、Computational methods 计算模型
- finite state machines (morphological analysis, POS tagging)
- grammars and parsing (CKY, statistical parsing)
- probabilistic models and machine learning (HMMS, PCFGs, logistic regression, neural networks)
- vector spaces (distributional semantics)
- lambda calculus (compositional semantics)
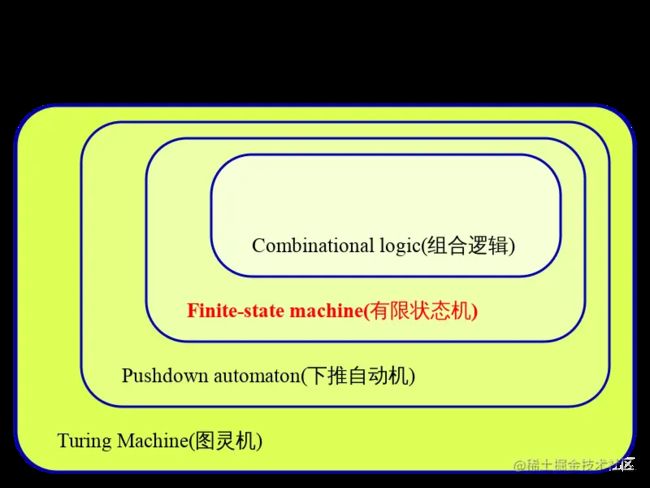
1. 有限状态机 finite state machines
状态机一般指有限状态机（英语：finite-state machine，缩写：FSM）又称有限状态自动机（英语：finite-state automaton，缩写：FSA），是表示有限个状态以及在这些状态之间的转移和动作等行为的数学计算模型。
有限状态机是在自动机理论和计算理论中研究的一类自动机。如下图所示，有限状态机归属于自动机理论范畴，从下面的自动机理论的领域分层图可以看出，越往外层，概念越复杂。
状态机中有几个术语：state(状态) 、transition(转移) 、action(动作) 、transition condition(转移条件) 。
- state(状态) ：将一个系统离散化，可以得到很多种状态，当然这些状态是有限的。例如：门禁闸机可以划分为开启状态、关闭状态；电扇可以划分为关、一档、二档、三档等状态。
- transition(转移) ：一个状态接收一个输入执行了某些动作到达了另外一个状态的过程就是一个transition(转移)。定义transition(转移)就是在定义状态机的转移流程。
- transition condition(转移条件) ：也叫做Event(事件)，在某一状态下，只有达到了transition condition(转移条件)，才会按照状态机的转移流程转移到下一状态，并执行相应的动作。
- action(动作)：在状态机的运转过程中会有很多种动作。如：进入动作(entry action)[在进入状态时进行]、退出动作(exit action)[在退出状态时进行]、转移动作[在进行特定转移时进行]。
- emissions 输出: letters produced at each transition
下图，就定义了一个只有opened 和closed两种状态的状态机。当系统处于opened状态，在收到输入“关闭事件”，达到了状态机转移条件，系统就转移到了closed状态，并执行相应的动作，此例有一个进入动作(entry action)，进入closed状态，会执行close door动作。
有限状态机数学模型为(Σ, S, s0, δ, F)：
- Σ，alphabet表示有效输入
- S 有限的，非空的一组状态
- s0 初始状态，S的一个元素
- δ，transition表示从一种状态到另一种状态的规则方法
- F是一组有限状态，是S的子集（可能为空）
- O一组输出（可能为空）
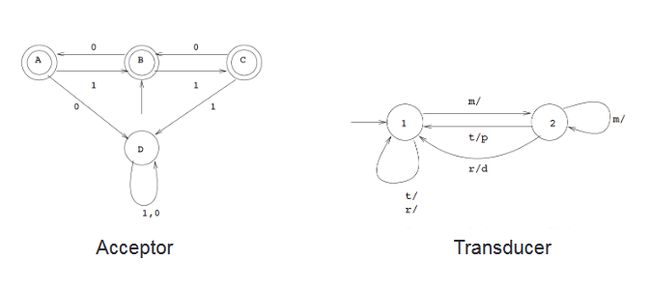
以售票机为例：
- Σ (m, t, r) ： 付款m, 出票t, 退款r
- S (1, 2) : 没付款状态, 付款状态
- s0 (1) ：初始状态
- δ (shown below) : transition function: δ : S x Σ → S
- F : empty
- O (p/d) :打印票据p, 退款d
有限状态机可以被分为不同的类型，主要可以被分为：acceptors(接收器)、transducers(转换器) 两大类。
Acceptors(接收器) 产生二进制输出，指示是否接受接收到的输入。接受者的每个状态要么接受（accepting）要么不接受（non accepting）。一旦接收到所有输入，如果当前状态为接受（accepting）状态，则该输入被接受;否则将被拒绝。通常，输入是一个符号(字符)序列；没有动作(actions)。
如下图是一种acceptors(接收器) 类型有限状态机，用来识别所输入的字符串是否为nice，其总共被划分为了七种状态，其中只有第七种状态Success被认为是可接受状态。如果所输入的字串不是nice，则会被转移到第六种状态Error。
如下给出acceptors(接收器) 的数学形式化定义，acceptors(接收器) 型有限状态机是一个五元组(Σ,S,s0,δ,F) 其中：
- Σ 是输入字符集合(有限的非空符号集合)；
- S 是有限非空状态集合；
- s0 是初始状态，属于 S 中的元素；
- δ 是状态转移函数：δ：S×Σ→ S；
- F 是最终状态集合，是 S 的子集。
Transducers(转换器) 根据给定的输入与/或使用动作的状态产生输出，输出的同时可能也伴随着状态的转移(不是必须)。应用在控制系统，在控制系统又分为两种：moore machine (摩尔型有限状态机)和mealy machine (米利型有限状态机)
- 若输出只和状态有关而与输入无关，则称为moore状态机
- 输出不仅和状态有关而且和输入有关系，则称为mealy状态机
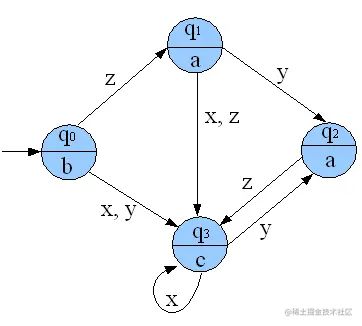
1.1 moore状态机 (moore machine)
如下所示的状态机为moore状态机，其有q0、q1、q2、q3四个状态，X,Y,Z三个输入，a、b、c三个输出。可以看出其四个状态q0、q1、q2、q3对应的输出分别为b、a、a、c，就是说输出已经和状态绑定好，不管输入为哪一个，均不影响输出。其中q0为初始状态，假设输入为XYZY，可以看出输出为bcac；假设输入为ZXYZ，则输出为baca，可以看出，虽然输出只和状态有关而与输入无关，但改变输入的序列顺序，输出序列也会改变。
1.2 mealy状态机
mealy状态机的输出与当前状态和输入都有关。但是对于每个mealy状态机都有一个等价的moore机。如下所示为一个简单的mealy状态机，它有一个输入和一个输出。在每一个有向边上，标注出了输入(红色)和输出(蓝色)。这个状态机的初始状态为Si，当输入为0，输出0，状态变为S0，接着输入0，输出0，状态还是为S0，在此状态下一直输入0，输出会一直是0，但输入为1是，输出才为1，状态变为S1，在此状态再接着输入1，输出一直还是0，直到遇到输入为0，输出才变为1。此状态机其实实现了一个边缘触发检测器，每次输入从1到0或是从1到0发生跳变时，输出为1否则输出为0。如下所示时序图，当输入为0111001110时，输出为0100101001。
如下给出transducers(转换器) 的数学形式化定义，transducers(转换器) 型有限状态机是一个六元组(Σ, Γ, S, s0, δ, ω),其中：
- Σ 是输入字符集合(有限的非空符号集合)；
- Γ 是输出字符集合(有限的非空符号集合)；
- S是有限非空状态集合；
- s0是初始状态，属于S中的元素；
- δ是状态转移函数：δ：S×Σ→S；
- ω 是输出函数。
如果输出函数 ω 依赖于状态和输入(ω:S×Σ→Γ)，则定义的是mealy状态机；如果输出函数仅仅依赖于状态(ω:S→Γ)，那么定义的是moore状态机。如果，有限状态机没有输出函数 ω 这一项，那么可以称作transition system(转移系统) 。很多应用程序用到的有限状态机并没有输出序列，仅仅用到了状态机的转移过程和动作，其实可以称为转移系统。
1.3 代码
1.3.1 简单有限状态机
class Transition:
"""A change from one state to a next"""
def __init__(self, current_state, state_input, next_state):
self.current_state = current_state
self.state_input = state_input
self.next_state = next_state
def match(self, current_state, state_input):
"""Determines if the state and the input satisfies this transition relation"""
return self.current_state == current_state and self.state_input == state_input
class FSM:
"""A basic model of computation"""
def __init__(
self,
states=[],
alphabet=[],
accepting_states=[],
initial_state=''):
self.states = states
self.alphabet = alphabet
self.accepting_states = accepting_states
self.initial_state = initial_state
self.valid_transitions = False
def add_transitions(self, transitions=[]):
"""Before we use a list of transitions, verify they only apply to our states"""
for transition in transitions:
if transition.current_state not in self.states:
print(
'Invalid transition. {} is not a valid state'.format(
transition.current_state))
return
if transition.next_state not in self.states:
print('Invalid transition. {} is not a valid state'.format)
return
self.transitions = transitions
self.valid_transitions = True
def __accept(self, current_state, state_input):
"""Looks to see if the input for the given state matches a transition rule"""
# If the input is valid in our alphabet
if state_input in self.alphabet:
for rule in self.transitions:
if rule.match(current_state, state_input):
return rule.next_state
print('No transition for state and input')
return None
return None
def accepts(self, sequence):
"""Process an input stream to determine if the FSM will accept it"""
# Check if we have transitions
if not self.valid_transitions:
print('Cannot process sequence without valid transitions')
print('Starting at {}'.format(self.initial_state))
# When an empty sequence provided, we simply check if the initial state
# is an accepted one
if len(sequence) == 0:
return self.initial_state in self.accepting_states
# Let's process the initial state
current_state = self.__accept(self.initial_state, sequence[0])
if current_state is None:
return False
# Continue with the rest of the sequence
for state_input in sequence[1:]:
print('Current state is {}'.format(current_state))
current_state = self.__accept(current_state, state_input)
if current_state is None:
return False
print('Ending state is {}'.format(current_state))
# Check if the state we've transitioned to is an accepting state
return current_state in self.accepting_states
2. 状态机生成语言
2.1 regular languages and regular expressions and Chomsky Hierarchy
- Languages produced by FSMs are called regular languages
- Reg. languages can also be described with regular expressions 正则表达式.
- 正式地，一个正则表达式包含以下运算：
- 从字母集中抽样得到的符号：Σ
- 空字符串：ε
- 两个正则表达式的连接：RS
- 两个正则表达式的交替：R∣S
- 星号表示出现 0 次或者重复多次：R∗
- 圆括号定义运算的有效范围：()
- Chomsky Hierarchy: four major classes of formal languages
3. regular 正则语言 (generated by finite state machines, usually assumed sufficient to describe phonology and morphology)
2. 上下文无关 (context-free) (和正则语言相比，它具有更少的约束，可能捕获更多的自然语言的特性)
1. 上下文敏感 (Context Sensitive) (possibly needed for some natural language phenomena)
0. recursively enumerable (anything a computer program can produce)
判断正则和非正则语言：
- 一个语言是正则的当且仅当它能被有穷自动机接受
- 正则语言共有而非正则语言不具备的两条性质：
- 从左到右扫描一个字符串时，为了确定这个字符串最终是否在该语言中，所需要的存储量必须是
有界的、事先固定的且只与该语言有关而与具体的输入字符串无关的。 - 有无穷多个字符串的正则语言用带
圈的有穷自动机或含Kleene星号的正则表达式表示。这样的语言一定有具有某种简单的重复构造的无穷子集。
比如，
或者 {
且是一个素数} 都是非正则的
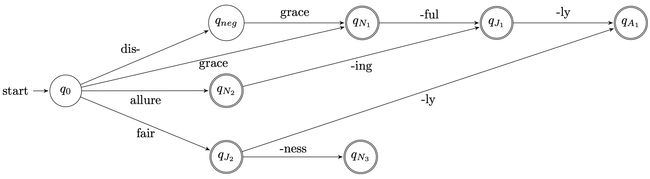
2.2 状态机FSM用于形态学分析（morphological analysis）
2.2.1 有限状态接收器（Finite state acceptors，FSA）
FSA 包含：
- 输入符号的字母集：Σ
- 状态集合：Q
- 起始状态：q0 ∈ Q
- 最终状态：F ⊆ Q
- 转移函数：符号和状态 → 下一个状态
Build components as separate FSAs
- – L: FSA for lexicon
- – D: FSA for derivational morphology
- – I: FSA for inflectional morphology
Concatenate L + D + I (there are standard algorithms)
2.2.2 有限状态转换器（Finite State Transducers，FST）
FST 在 FSA 的基础上增加了字符串的输出能力：
- 包含一个 输出字母集（output alphabet）
- 现在，转移函数会采用输入符号并发出输出符号 (Q,Σ,Σ,Q)
其中，第一个 Q 表示输入状态，最后一个 Q 表示输出状态，第一个 Σ 表示输入字母集，第二个 Σ 表示输出字母集。
3. Edit distance algorithm 一种动态规划
编辑距离（Minimum Edit Distance，MED），由俄罗斯科学家 Vladimir Levenshtein 在1965年提出，也因此而得名 Levenshtein Distance。在信息论、语言学和计算机科学领域，Levenshtein Distance 是用来度量两个序列相似程度的指标。通俗地来讲，编辑距离指的是在两个单词
在这里定义的单字符编辑操作有且仅有三种：
- 插入（Insertion）
- 删除（Deletion）
- 替换（Substitution）
一般时候，可以设置插入和删除cost值为1，替换cost值为2.
譬如，"kitten" 和 "sitting" 这两个单词，由 "kitten" 转换为 "sitting" 需要的最少单字符编辑操作有：
1.kitten → sitten (substitution of "s" for "k")
2.sitten → sittin (substitution of "i" for "e")
3.sittin → sitting (insertion of "g" at the end)
因此，"kitten" 和 "sitting" 这两个单词之间的编辑距离为 3 。
4. 编辑距离自动机 (Edit Distance Automata)
其中，δ 是状态转移的记分函数，在编辑距离的 WFST（加权FST） 实现下，我们只需要一个状态 q。上面的式子表明：将 a 替换为 a 或者将 b 替换为 b 的代价为 0；将 a 替换为 b 或者将 b 替换为 a 的代价为 1；将 a 删除或者将 b 删除的代价为 1；插入一个 a 或者 b 的代价为 1。
5. 下推自动机（PushDown Automaton，PDA）：自带栈的有限状态机
为什么要在有限自动机的基础上给其增加一个栈来构建下推自动机呢？其根本原因在于有限状态机本身无法存储数据，而加上了栈之后的下推自动机则具有了数据存储能力。具有了存储能力之后，下推自动机的计算能力相较于有限自动机得到了进一步的增强。
我们已经知道，有限自动机在进行状态转移的时候，需要读取一个输入，然后根据当前状态已经输入来进行状态转移。下推自动机在进行状态转移的时候同样要依赖于当前状态和输入，不过，因为下推自动机有了栈的概念，所以在进行状态转移的时候我们还需要一点别的东西 —— 读栈和写栈操作。例如下图这样的一个下推自动机：
我们可以把这个下推自动机用这样的转移列表列出来，注意这里的 $ 符号，因为栈为空的状态并不是很好判断，所以我们添加了这个字符来代表栈为空，也就是说栈的最底部永远应该保持有 $ 这个字符。最下面的虚线代表着当栈为空且状态为 2 时（我们使用虚线来代表不需要有输入的转移情形，即自由移动），此时不需要任何输入，栈会自动的弹出 $ 然后再压入 $，随后状态从 2 变为 1。
| 当前状态 | 输入字符 | 转移状态 | 栈顶字符（读入 / 弹出） | 压入字符 |
|---|---|---|---|---|
| 1 | ( | 2 | $ | b$ |
| 2 | ( | 2 | b | bb |
| 2 | ) | 2 | b | 不压入 |
| 2 | 无输入 | 1 | $ | $ |
四、语言模型
n-gram模型、隐马尔可夫模型（HMM）和条件随机场（CRF）
1. n-gram模型
1.1 unigram（bag-of-words）模型
如何计算单词概率，用极大似然估计：
1.2 bigram 或 trigram模型
MLE计数估计概率参数
trigram: 
对于给定x_i-1, 所有可能的x_i 概率之和为一：
要注意p(xi,xi-1)中x的顺序！
2. 平滑方法（smoothing） 概率计数
平滑策略的引入，主要使为了解决语言模型计算过程中出现的零概率问题。零概率问题又会对语言模型中N-gram模型的Perplexity评估带来困难。
- Additive smoothing：Add-one smoothing / 加一或加权平滑
- Good-Turing estimate
- Jelinek-Mercer smoothing (interpolation) 插值
2.1 Add-one smoothing 加一平滑，拉普拉斯平滑
Add-α smoothing:
与贝叶斯估计(bayesian estimation)形态近似，dirichlet prior
2.2 Good-Turing smoothing
基本思想: 用观察计数较高的 N-gram 数量来重新估计概率量大小，并把它指派给那些具有零计数或较低计数的 N-gram
2.3 卡茨退避法(Katz backoff)
Katz平滑方法通过加入高阶模型与低阶模型的结合，扩展了Good-Turing估计方法。
当某一事件在样本中的频率大于k时，运用最大似然估计MLE经过减值来估计其概率。当某一事件的频率小于k时，运用低阶的语法模型作为代替高阶语法模型的后备，而这种代替必须受归一化因子α的作用。根据低阶的语法模型分配由于减值而节省下来的剩余概率给未见事件，这比将剩余概率均匀分配给未见事件更合理。
2.4 Interpolation 线性插值（Jelinek-Mercer 插值）
简单来讲，就是把不同阶的模型结合起来:用线性差值把不同阶的 N-gram 结合起来，这里结合了 trigram，bigram 和 unigram。用 lambda 进行加权:
2.5 绝对减值法（Absolute Discounting）
- 从每个 观测到的 n-gram 计数中 “借” 一个 固定的概率质量（a fixed probability mass） d。（因为对于add-one平滑来说出现次数多的词汇会损失更多有效计数）
- 然后将其 重新分配（redistributes） 到 未知的 n-grams 上。
和Add-one平滑一样，如果我们想计算 Absolute Discounting 平滑概率，只需要用 Absolute Discounting 平滑下的有效计数除以上下文在语料库中出现的总次数即可
2.6 Kneser-Ney Smoothing
Kneser-Ney 平滑采用的方法是基于当前单词 在多少个 不同的上下文 中出现过，或者说是基于该单词的 多功能性（versatility）或者 延续概率（continuation probability）。
对比 Katz Backoff 的概率公式，在 Kneser-Ney 平滑概率公式中，只有一项不同：
其中，
可以看到，对于观测到的 n-grams，Kneser-Ney 概率和 Katz Backoff 概率两者是相同的。而对于那些未知的 n-grams，Kneser-Ney 概率中从观测 n-grams 中 “借来” 的概率质量 
与之前一样保持不变，而之前关于低阶模型 
的部分则由我们所说的延续概率 
来替代。
在延续概率的计算公式中：分子部分计算的是一共有多少个 唯一 的上下文单词w_i-1 和当前单词w_i 共同出现过（co-occurrence）；而分母部分就是将所有可能的单词 w_i 对应的不同共现上下文单词数量（即分子部分）进行一个累加。
3. 对数线性模型(Log-linear Model)
Log-linear语言模型的本质是把语言模型的建立看作是一个多元分类问题，核心是从上文中提取特征。
形式化地说，假设上文为
，log-linear语言模型需要一个特征函数
，其将上文信息作为输入，输出一个N 维特征向量（注意这里是feature vector而不是eigenvector）
，这个特征向量x就是对上文信息的一个表示（这里的N不是N元语法里面的那个N，不表示上文单词数量！）
log-linear语言模型还允许灵活加入其它特征，这也是该模型的一大长处。常见的特征还包括
- 上文的语义类别。可以使用聚类方法将相似单词聚类，这样，上文每个单词的独热编码不再是单词表长度，而是聚类得到的类别个数
- 上文单词的其它语义信息，例如词性标注（POS-Tag）信息
- 词袋特征。此时，不止考虑前面少数几个单词，而是考虑前面所有单词，统计它们出现的个数。注意在这种情况下会失去单词的位置信息，不过可以捕捉到单词的共现信息
Part I: Words
* Inflectional and derivational morphology//
* Finite state methods and Regular expressions//
* Bag-of-Words models and their applications
* Word Classes and Parts of speech
* Sequence Models (n-gram and Hidden Markov models, smoothing)
* The Viterbi algorithm, Forward Backward, EM
Part II: Syntax
* Syntactic Concepts (e.g., constituency, subcategorisation, bounded and unbounded dependencies, feature representations)
* Analysis in CFG - Greedy algorithms---Shift-reduce parsing
* Divide-and-conquer algorithms---CKY
* Lexicalised grammar formalisms (e.g., CCG, dependency grammar)
* Statistical parsing (PCFGs, dependency parsing)
Part III: Semantics and Discourse
* Logical semantics and compositionality
* Semantic derivations in grammar
* Lexical Semantics (e.g., word embeddings, word senses, semantic roles)
* Discourse (e.g., anaphora)
1. Introduction, words, and morphology • Including: ambiguity, words, and morphology//
2. Basic algorithms • Including: finite state models, dynamic programming, and edit distance
3. Language models • Including: probability, N-gram models, smoothing, perplexity
4. Text classification • Including: Naïve Bayes, logistic regression, basic neural networks, evaluating classifiers
5. Tagging and hidden Markov models • Including: parts of speech, HMMs, Viterbi algorithm
6. Phrase-structure syntax and parsing • Including: syntactic structure, context free grammars, and the CKY algorithm
7. Beyond basic grammars • Including: probabilistic grammars and parsing, dependency parsing, evaluating parsers
8. Lexical semantics and word embeddings • Including: word senses, distributional semantics, mutual information, word embeddings
9. Sentence-level semantics • Including: logical forms, coreference
References
集合：
https://blog.csdn.net/bensonrachel/category_8109347.html
multi language NLP - 知乎
Archive - YEY 的博客 | YEY Blog
单篇：
语言学小知识－什么是语素 - 知乎
什么是状态机？一篇文章就够了 - 掘金
自然语言处理 03：N-gram 语言模型 - YEY 的博客 | YEY Blog
词性标注(Part-of-Speech Tagging),HMM - 知乎