完全背包理论基础 518.零钱兑换II

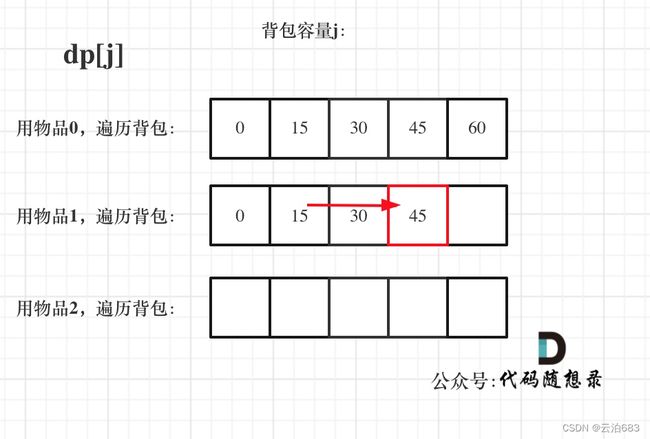
完全背包理论基础 

01背包是每个物品只能放一次，而完全背包是每个物品都能重复放入多次。

01背包

    for(int i = 0; i < weight.size(); i++) { // 遍历物品
        for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
            dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
        }

 完全背包

// 先遍历背包，再遍历物品
for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量（也可向物品后容量，01背包不行）
    for(int i = 0; i < weight.size(); i++) { // 遍历物品
        if (j - weight[i] >= 0) dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
    }
    cout << endl;
}

对比代码，01背包的一维代码是向物品后容量，而且遍历背包容量的时候是倒序，防止放入多次重复物品

而完全背包是物品和容量的遍历顺序可随意替换，而且由于可放入多次重复物品，所以都是正序遍历

为什么完全背包（一维）的物品和容量的遍历顺序可随意替换，而01背包（一维）不行？

01背包的一维必须要向物品再容量遍历，是因为.....

先物品后容量

#include 
#include 
using namespace std;
void test_1_wei_bag_problem_capacity_first() {
    vector weight = {1, 3, 4};
    vector value = {15, 20, 30};
    int bagWeight = 4;
    // 初始化
    vector dp(bagWeight + 1, 0);
    for (int i = 0; i < weight.size(); i++) {  // 先遍历物品
        for (int j = bagWeight; j >= weight[i]; j--) {  // 再遍历容量
            dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
        }
    }
    // 输出每次遍历的数组
    for (int j = 0; j <= bagWeight; j++) {
        cout << dp[j] << " ";
    }
    cout << endl << "Final Result: " << dp[bagWeight] << endl;
}
int main() {
    test_1_wei_bag_problem_capacity_first();
    return 0;
}

0 15 15 20 35 
Final Result: 35

先容量后物体

#include 
#include 
using namespace std;
void test_1_wei_bag_problem_capacity_first() {
    vector weight = {1, 3, 4};
    vector value = {15, 20, 30};
    int bagWeight = 4;
    // 初始化
    vector dp(bagWeight + 1, 0);

    for (int j = 4; j >= weight[i]; j--) {  // 先遍历容量
        for (int i = 0; i < weight.size(); i++) {  // 再遍历物品
            if (j >= weight[i]) {
                dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
            }
        }
    }
    // 输出每次遍历的数组
    for (int j = 0; j <= bagWeight; j++) {
        cout << dp[j] << " ";
    }
    cout << endl << "Final Result: " << dp[bagWeight] << endl;
}
int main() {
    test_1_wei_bag_problem_capacity_first();
    return 0;
}

0 0 0 0 30 
Final Result: 30

还是整不明白，卡哥的原文是

“再来看看两个嵌套for循环的顺序，代码中是先遍历物品嵌套遍历背包容量，那可不可以先遍历背包容量嵌套遍历物品呢？

不可以！

因为一维dp的写法，背包容量一定是要倒序遍历（原因上面已经讲了），如果遍历背包容量放在上一层，那么每个dp[j]就只会放入一个物品，即：背包里只放入了一个物品。”

而完全背包推导一遍会发现dp[j]都使用其左侧的值计算，正序时不管是先背包后容量还是先容量再背包的遍历，正在计算的值，其左侧的值都是早就被计算出来了的，而正在计算的值也就利用其左侧的值计算。（图顺序分别是先物品后容量，先容量后物体）

518.零钱兑换II

题目：

给定一个不同面额的硬币组合和一个目标值，每种面额的数量有无数个，求硬币组合的总额到达目标值的组合数量。

dp[j]含义：

dp[j]：凑成总金额j的货币组合数为dp[j]

递推公式：

求装满背包有几种方法（组合，排列数）用：dp[j] += dp[j - coins[i]];

初始化:

dp[0]=1

遍历顺序：

先物品后背包：最大组合数

先背包后物品：最大排列数

总代码：

class Solution {
public:
    int change(int amount, vector& coins) {
        vector dp(amount + 1, 0);
        dp[0] = 1;
        for (int i = 0; i < coins.size(); i++) { // 遍历物品
            for (int j = coins[i]; j <= amount; j++) { // 遍历背包
                dp[j] += dp[j - coins[i]];
            }
        }
        return dp[amount];
    }
};