最小二乘法的无偏估计

最小二乘法的无偏估计

目前我已知的最小二乘估计法有两种，第一种是基本的最小二乘法，对于白噪声，这类方法可以得到无偏估计。但对于有色噪声，这类方法只能得到有偏估计。为了解决这个问题，就导致了第二类最小二乘法的产生。这类改进算法可以在有色噪声下也能得到无偏估计。

1. 噪声视为白噪声的最小二乘法
   • 一般最小二乘法
   • 加权最小二乘法
   • 递推最小二乘法（RLS）
   • 渐消记忆RLS法
2. 噪声视为有色噪声的最小二乘法
   • 广义最小二乘法（GLS）
   • 增广最小二乘法（RELS）
   • 多级最小二乘法（MSLS）

这篇主要介绍改进后的最小二乘法。 在进入正题之前，先简要阐述白噪声和有色噪声的区别：

• 白噪声：不同时刻的噪声是不相关的，自相关函数为脉冲函数；
• 有色噪声：不同时刻的噪声之间存在相关性。在工程实践中，往往是这类噪声。

1.广义最小二乘法（GLS）

1.1.系统模型

系统模型如下所示：
$$A(q^{-1})y(k)=B(q^{-1})u(k)+\epsilon (k),\epsilon (k)=\frac{\xi (k)}{C(q^{-1})}\text{\hspace{1em}(1)}$$
上式中，$\xi (k)$为白噪声，$\epsilon (k)$为有色噪声序列。三个多项式形式如下所示：
$$\begin{array}{r}A(q^{-1})=1+a_1{q}^{-1}+...+a_{n_a}{q}^{-n_a}\\ B(q^{-1})=b_0+b_1{q}^{-1}+...+b_{n_b}{q}^{-n_b}\\ C(q^{-1})=1+c_1{q}^{-1}+...+c_{n_c}{q}^{-n_c}\end{array}\text{\hspace{1em}(2)}$$
设系统的输入为白噪声$\xi (k)$，输出为有色噪声$\epsilon (k)$，这种线性系统通常称为形成滤波器，如式(1)。

把式(1)进行等效变换后，可以得到式(3)：
$$A(q^{-1})C(q^{-1})y(k)=B(q^{-1})C(q^{-1})u(k)+\xi (k)\text{\hspace{1em}(3)}$$
我们再把上式简化一下，令$\{\begin{array}{l}\bar{y}(k)=C(q^{-1})y(k)\\ \bar{u}(k)=C(q^{-1})u(k)\end{array}$，就可以得到式(4)：
$$A(q^{-1})\bar{y}(k)=B(q^{-1})\bar{u}(k)+\xi (k)\text{\hspace{1em}(4)}$$

此时的噪声$\xi (k)$已经是白噪声，可以直接使用LS法对系统参数进行无偏估计。

1.2.噪声模型

式(4)就是GLS的关键公式。但为了获得这个公式，我们必然先得到$C(q^{-1})$，这就需要我们对噪声模型进行估计。

根据系统模型表达式(1)，可以得到关于噪声的差分方程描述：
$$\begin{array}{rl}\epsilon (k)=\frac{1}{C(q^{-1})}\xi (k)& ⟹C(q^{-1})\epsilon (k)=\xi (k)\\ & ⟹\epsilon (k)=-c_1\epsilon (k-1)-...c_{n_c}\epsilon (k-n_c)+\xi (k)\end{array}$$
由上式得到$N$个方程，将其写成矩阵形式如下：
$$\epsilon =\Omega f+\xi$$
根据最小二乘法，我们可以得到$C(q^{-1})$的估计值$f$：
$$f=({\Omega }^T\Omega {)}^{-1}{\Omega }^T\epsilon$$
但这里存在一个问题：我们无法对噪声进行直接测量。也就是说，我们无法得到$\Omega ,\epsilon$。

一种方法是对误差进行估计，用残差$e(k)$代替噪声$\epsilon (k)$：
$$e(k)=\hat{A}(q^{-1})y(k)-\hat{B}(q^{-1})u(k)\text{\hspace{1em}(5)}$$
以上公式(3)、(4)、(5)就是推导GLS的主要公式了。

1.3.主要步骤

广义最小二乘法的基本思想：

• 先不考虑有色噪声，用一般LS法估计系统参数$a_i,b_i$，得到有偏估计${\hat{a}}_i^{(1)},{\hat{b}}_i^{(1)}$；
• 再用有偏估计${\hat{a}}_i^{(1)},{\hat{b}}_i^{(1)}$去估计噪声模型$c_i$；
• 已知噪声模型后，根据等式(4)再去估计系统参数${\hat{a}}_i^{(2)},{\hat{b}}_i^{(2)}$；

以上反复迭代后即可得到系统参数的无偏估计。

(1)用一般LS法得到系统参数的有偏估计

在GLS一开始，我们先不考虑噪声是白噪声还是有色噪声，直接当作白噪声用LS法进行估计，当然这次的估计值不会很准确，因为是一个有偏估计。但作为参数估计的初始值已经可以了，后面会再进行修正。
$$A(q^{-1})y(k)=B(q^{-1})u(k)+\epsilon (k)$$
第一次参数估计的结果为
$${\hat{\theta }}^{(1)}=({\Phi }^T\Phi {)}^{-1}{\Phi }^{T}y$$

(2)用估计值$\hat{\theta }$估计噪声模型参数$f$

在已有系统参数估计值的情况下，通过式(5)，就可以得到噪声$\epsilon (k)$的估计值$e(k)$。根据$N$个等式(5)，我们可以得到

• $\Omega$：$N\times n_c$；
• $e$：$N\times 1$；

然后使用LS法对噪声参数进行估计，结果为
$${\hat{f}}^{(1)}=({\Omega }^T\Omega {)}^{-1}{\Omega }^{T}e$$

(3)用噪声估计参数$\hat{f}$对系统估计参数$\hat{\theta }$进行修正

得到噪声模型后，我们就可以得到$\bar{y}(k),\bar{u}(k)$，然后应用式(4)，通过最小二乘法对系统参数进行修正：
$${\hat{\theta }}^{(2)}=({\bar{\Phi }}^T\bar{\Phi }{)}^{-1}{\bar{\Phi }}^T\bar{y}(k)$$
最后，重复步骤(2)~(3)，直到估计值${\hat{\theta }}^{(i)}$收敛。

2.增广矩阵法（RELS）

2.1.系统模型与公式推导

考虑这样的一个系统（注意GLS和RELS的系统模型的差别）：
$$A(q^{-1})y(k)=B(q^{-1})u(k)+C(q^{-1})\xi (k)\text{\hspace{1em}(1)}$$
上式中，$\xi (k)$是新息序列，具有白噪声特征。三个多项式形式如下所示：
$$\begin{array}{r}A(q^{-1})=1+a_1{q}^{-1}+...+a_{n_a}{q}^{-n_a}\\ B(q^{-1})=b_0+b_1{q}^{-1}+...+b_{n_b}{q}^{-n_b}\\ C(q^{-1})=1+c_1{q}^{-1}+...+c_{n_c}{q}^{-n_c}\end{array}\text{\hspace{1em}(2)}$$
增广矩阵法的特点是把噪声模型参数也加入到了估计参数中，相当于扩充被估计参数的维数，然后再用最小二乘法同时估计系统参数和噪声参数。
$$\theta ={\left[\begin{array}{ccccccccc}{a}_1& ...& a_{n_a}& b_0& ...& b_{n_b}& c_1& ...& c_{n_c}\end{array}\right]}^T$$
根据式(1)，我们可以得到以下形式：
$$y(k)={\Psi }_k^T\theta +\xi (k),k=n+1,...,n+N\text{\hspace{1em}(3)}$$

$${\Psi }_k={\left[\begin{array}{ccccccccc}-y(k-1)& ...& -y(k-n_a)& u(k)& ...& u(k-n_b)& \xi (k-1)& ...& \xi (k-n_c)\end{array}\right]}^T$$

把上式扩展为$N$个方程，就是一个标准的最小二乘法形式。但与广义最小二乘法遇到的问题一样，我们无法直接测量噪声数据，因此需要对$\xi (k)$进行估计。 方法也与GLS一样，用残差$e(k)$来估计噪声$\xi (k)$。
$${\Psi }_k={\left[\begin{array}{ccccccccc}-y(k-1)& ...& -y(k-n_a)& u(k)& ...& u(k-n_b)& \hat{\xi }(k-1)& ...& \hat{\xi }(k-n_c)\end{array}\right]}^T$$
根据式(3)，可以得到噪声的估计$\hat{\xi }(k)$表示为：
$$\hat{\xi }(k)=y(k)-{\Psi }_k^T\hat{\theta }\text{\hspace{1em}(4)}$$
根据递推最小二乘法的方式，我们可以得到增广矩阵法的递推方程：
$$\begin{array}{rl}{K}_{N+1}& =P_N{\hat{\Psi }}_{N+1}(1+{\hat{\Psi }}_{N+1}^T{P}_N{\hat{\Psi }}_{N+1}{)}^{-1}\\ P_{N+1}& =P_N-K_{N+1}{\hat{\Psi }}_{N+1}^T{P}_N\\ {\hat{\theta }}_{N+1}& ={\hat{\theta }}_N+K_{N+1}(y_{N+1}-{\hat{\Psi }}_{N+1}^T{\hat{\theta }}_N)\end{array}\text{\hspace{1em}(5)}$$

3.GLS vs RELS

由上面可知，GLS和RELS对于有色噪声的处理方式是不同的，下式(1)与(2)分别是GLS和RELS对有色噪声的处理方法，$\xi (k)$为白噪声。
$$A(q^{-1})y(k)=B(q^{-1})u(k)+\epsilon (k),\epsilon (k)=\frac{1}{D(q^{-1})}\xi (k)\text{\hspace{1em}(1)}$$

$$A(q^{-1})y(k)=B(q^{-1})u(k)+\epsilon (k),\epsilon (k)=C(q^{-1})\xi (k)\text{\hspace{1em}(2)}$$

虽然两者对噪声的表示形式不同，但这并不会影响最后的参数估计结果。 在进行参数辨识时，系统参数的估计值应该是一致的，区别在于对噪声模型的估计会不一样。

下面对一组数据分别用GLS、RELS进行参数辨识。

系统模型如下所示，参数真值为$a_1=-1.5,a_2=0.7,b_0=0,b_1=1,b_2=0.5$：
$$y(k)+a_{1}y(k-1)+a_{2}y(k-2)=b_{0}u(k)+b_{1}u(k-1)+b_{2}u(k-2)+\epsilon (k)$$

$$\epsilon (k)=\xi (k)+c_1\xi (k-1)+c_2\xi (k-2)$$

上式的噪声表示形式与RELS的表示形式相同，可以直接用RELS进行参数辨识。RELS的辨识结果为
$$\hat{\theta }={\left[\begin{array}{ccccc}-1.5071& 0.7006& -0.0372& 1.0410& 0.4801\end{array}\right]}^T,J=40.6337$$

对于GLS，噪声$\epsilon (k)$可以设为另外一种形式，即
$$\epsilon (k)+f_1\epsilon (k-1)+f_2\epsilon (k-2)=\xi (k)⟹\epsilon (k)=\frac{1}{1+f_1{q}^{-1}+f_2{q}^{-2}}\xi (k)$$
GLS的辨识结果为
$$\hat{\theta }={\left[\begin{array}{ccccc}-1.5170& 0.7115& -0.0220& 1.0441& 0.4572\end{array}\right]}^T,J=40.7475$$

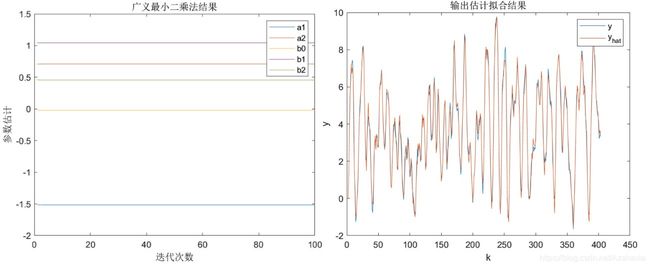
由上可见，虽然两种方式对噪声的表示方式不同，但它们最终得到的系统参数的估计结果是相近，最终都收敛到了真实值。