力扣第88题：合并两个有序数组（C语言题解）

果然学前端也逃不脱做算法题的宿命吗。。。。

萌新随机在互联网上随地乱丢一些赛博垃圾，还望拨冗批评扶正o.o

题目

当你没有思路时，准备使用最纯粹的力量

方法一：直接合并后排序

方法二：双指针

1.引入库

2.读入数据

方法二plus：逆向双指针

---

题目

给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2，另有两个整数 m 和 n ，分别表示 nums1 和 nums2 中的元素数目。

请你 合并 nums2 到 nums1 中，使合并后的数组同样按 非递减顺序 排列。

注意：最终，合并后数组不应由函数返回，而是存储在数组 nums1 中。为了应对这种情况，nums1 的初始长度为 m + n，其中前 m 个元素表示应合并的元素，后 n 个元素为 0 ，应忽略。nums2 的长度为 n 。

示例 1：

输入：nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
输出：[1,2,2,3,5,6]
解释：需要合并 [1,2,3] 和 [2,5,6] 。
合并结果是 [1,2,2,3,5,6] ，其中斜体加粗标注的为 nums1 中的元素。

示例 2：

输入：nums1 = [1], m = 1, nums2 = [], n = 0
输出：[1]
解释：需要合并 [1] 和 [] 。
合并结果是 [1] 。

示例 3：

输入：nums1 = [0], m = 0, nums2 = [1], n = 1
输出：[1]
解释：需要合并的数组是 [] 和 [1] 。
合并结果是 [1] 。
注意，因为 m = 0 ，所以 nums1 中没有元素。nums1 中仅存的 0 仅仅是为了确保合并结果可以顺利存放到 nums1 中。

提示：

• nums1.length == m + n
• nums2.length == n
• 0 <= m, n <= 200
• 1 <= m + n <= 200
• -109 <= nums1[i], nums2[j] <= 109

进阶：你可以设计实现一个时间复杂度为 O(m + n) 的算法解决此问题吗？

当你没有思路时，准备使用最纯粹的力量

直接使出无中生有，创建一个新数组 nums3，并无脑为其开辟 200 的空间，从头开始对比 nums1 和 nums2 ，按非递减顺序将元素一个一个地放到新数组中，如果出现其中一个数组已经放完，另一个数组还有元素没动，那么久把剩下的元素一股脑地全都塞给 nums3。最后直接打出一套 for 循环潇洒地把 nums3 复制给 num1，美美收工。

void merge(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n){
    int nums3[200] = {0};
    int key1 = 0,key2 = 0,key3 = 0;
    while(key1 < m && key2 < n)
    {
        if(nums1[key1] <= nums2[key2])
        {
            nums3[key3] = nums1[key1];
            key1++;
            key3++;
        }
        else
        {
            nums3[key3] = nums2[key2];
            key2++;
            key3++;
        }
    }
    while(key1 < m)
    {
        nums3[key3] = nums1[key1];
        key1++;
        key3++;
    }
    while(key2 < n)
    {
        nums3[key3] = nums2[key2];
        key2++;
        key3++;
    }
    for(int i = 0;i < nums1Size;i++)
    {
        nums1[i] = nums3[i];
    }
}

复杂度分析：

时间复杂度：O(m+n)，创建新数组阶段，指针均单向递增，最后使用 for 循环将 nums3 复制给 nums1。 

空间复杂度：O(1)，直接开辟 200 空间的新数组 nums3，主打一个空间挥霍。

方法一：直接合并后排序

void merge(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n) {
    for (int i = 0; i != n; i++) {
        nums1[m + i] = nums2[i];
    }
    //这里自行选择排序方式将nums1数组内元素按非递减顺序排列
}

复杂度分析（选用快速排序时）：

时间复杂度：O((m+n)log⁡(m+n))。 排序序列长度为 m+n，如果选择使用快速排序，时间复杂度平均情况为 O((m+n)log⁡(m+n))。

空间复杂度：O(log⁡(m+n))。 排序序列长度为 m+n，套用快速排序的空间复杂度即可，平均情况为 O(log⁡(m+n))。

方法二：双指针

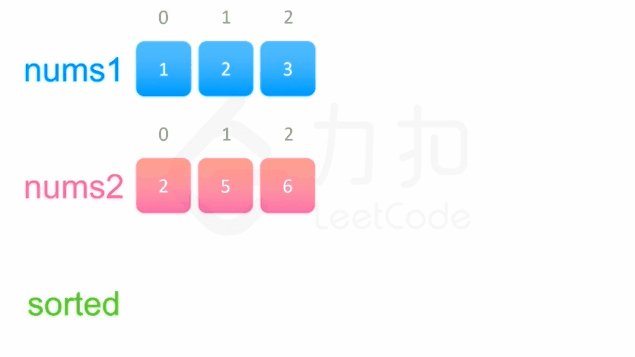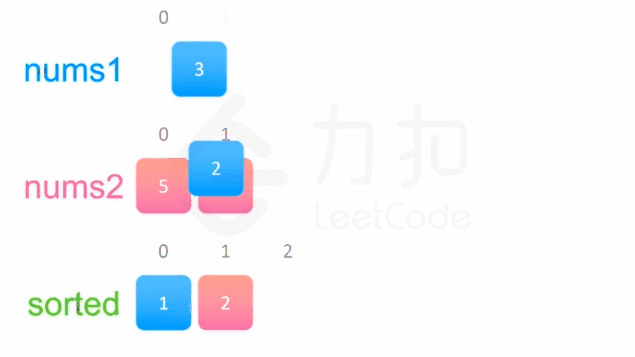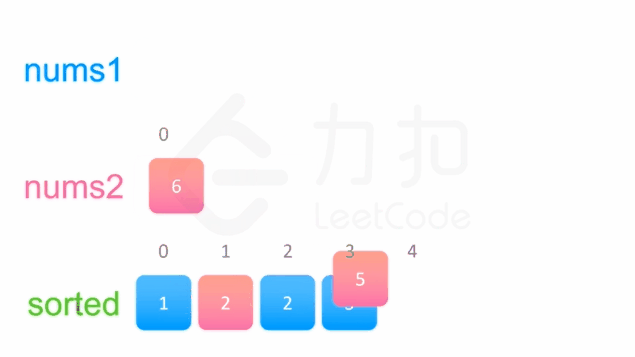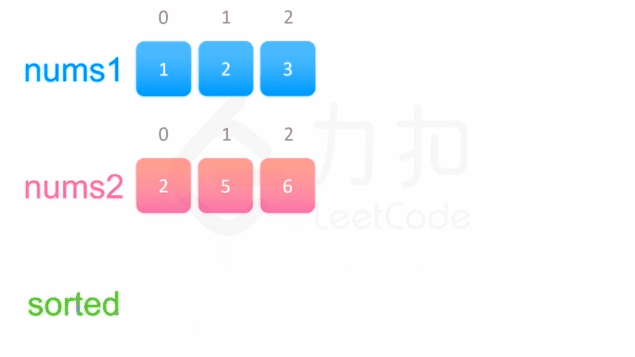
方法一没有利用数组已经被排序的性质。为了利用这一性质，我们可以使用双指针方法。这一方法将两个数组看作队列，每次从两个数组头部取出比较小的数字放到结果中。如下面的动画所示：

 

 为两个数组分别设置一个指针 p1与 p2来作为队列的头部指针。代码实现如下：

void merge(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n) {
    int p1 = 0, p2 = 0;
    int sorted[m + n];
    int cur;
    while (p1 < m || p2 < n) {
        if (p1 == m) {
            cur = nums2[p2++];
        } else if (p2 == n) {
            cur = nums1[p1++];
        } else if (nums1[p1] < nums2[p2]) {
            cur = nums1[p1++];
        } else {
            cur = nums2[p2++];
        }
        sorted[p1 + p2 - 1] = cur;
    }
    for (int i = 0; i != m + n; ++i) {
        nums1[i] = sorted[i];
    }
}

复杂度分析

时间复杂度：O(m+n)。 指针移动单调递增，最多移动 m+n 次，因此时间复杂度为 O(m+n)。

空间复杂度：O(m+n)。 需要建立长度为 m+n 的中间数组 sorted。 

---

方法二plus：逆向双指针

不另外创建一个数组，而是直接在比较的过程中将 nums2 和 nums1 中较大的数放在 nums1 的末尾，岂不美哉？

void merge(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n) {
    int p1 = m - 1, p2 = n - 1;
    int tail = m + n - 1;
    int cur;
    while (p1 >= 0 || p2 >= 0) {
        if (p1 == -1) {
            cur = nums2[p2--];
        } else if (p2 == -1) {
            cur = nums1[p1--];
        } else if (nums1[p1] > nums2[p2]) {
            cur = nums1[p1--];
        } else {
            cur = nums2[p2--];
        }
        nums1[tail--] = cur;
    }
}

复杂度分析

时间复杂度：O(m+n)。指针移动单调递减，最多移动 m+n次，因此时间复杂度为 O(m+n)。

空间复杂度：O(1)。不另外开辟空间。

力扣题目网址：力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

萌新不定期在互联网上随地乱丢一些赛博垃圾，还望拨冗批评斧正~