二叉树相关问题求解及其OJ巩固

前言：巩固二叉树的基础知识，前面学习了二叉树的相关性质，现在我们来解决二叉树的高度，结点数等问题。

一、二叉树基本概念求解

  假设有一个二叉树，那么我们应该如何知道它的高度、层数等相关信息，下面我们利用二叉树递归的本质来依次求解。

1 求二叉树总结点数量

（1）无返回值传计数变量地址

  求结点数目我们不能在函数里面创建临时计数变量，形参的改变不影响实参，递归的时候出来作用域就销毁了，因此我们需要传临时变量的地址。

void TreeSize(BTNode* root, int* size)
{
	if (root == NULL)
		return;
	*size += 1;
	TreeSize(root->left, size);
	TreeSize(root->right, size);
}

（2）带返回值的分治

  递归结束条件是结点为空，这时返回0，否则返回左右子树的结点数之和+1，这里的是计数的是根结点。

int TreeSize1(BTNode* root)
{
	if (root == NULL)
		return 0;
	return TreeSize1(root->left) + TreeSize1(root->right) + 1;
	//加一加的是根结点
}

2 求二叉树的高度

  二叉树可由其左子树和右子树构成，左右子树高度便能求出二叉树的高度。当根结点为空时，返回0，根节点不为空时，返回左右子树的较大的高度+1，加一是指加上根的那一层。

int TreeHeight(BTNode* root)
{
	if (root == NULL)
		return 0;
	int Left = TreeHeight(root->left);
	int Right = TreeHeight(root->right);
	int max = Left > Right ? Left : Right;
	return max + 1;
}//求高度

3 求第k层的结点数目

  第k层相对第一层需要往下递归k-1次，相对第二层需要递归k-2次，因此走到第k层需要递归k-1次，这时k==1。如果k>层数，提前走到空就返回 0。k为1时返回该结点1，否则返回左右子树之和。

int TreeKLevel(BTNode* root, int k)
{
	//走不到第k层就空了
	if (root == NULL)
		return 0;
		//当k=1时每次访问结点都返回1
	if (k == 1) //相对位置关系，走到第k层说明要走k-1次，目标层是k==1
		return 1;
	else
		return TreeKLevel(root->left, k - 1) + TreeKLevel(root->right, k - 1);
}

4 二叉树的层序遍历-队列

  二叉树的层数遍历我们需要用到队列先进先出的性质，如果根结点不为空，那么根节点入队。再把它的左右不为空的孩子入队，这时我们需要让左右孩子已经入队的双亲出队，这样左右孩子其中一个又变成了根节点，可以让其孩子入队。注意队列存的是结点的指针，有结点地址便能访问结点，不需要存整个结点。

void LevelOrder(BTNode* root)
{
	assert(root);
	Queue q;
	QueueInit(&q);
	if (root != NULL)
		QueuePush(&q, root);
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		printf("%d ", front->data);
		QueuePop(&q);
		if (front->left != NULL)
			QueuePush(&q, front->left);
		if (front->right != NULL)
			QueuePush(&q, front->right);
	}
	printf("\n");
	QueueDestroy(&q);
}

5 判断是否为完全二叉树

  有了上面层序遍历的经验，只有根结点不为空，我们把左右孩子均入队。

我们可以发现如果是完全二叉树，出队时遇到NULL,那么我们跳出循环的话，队列中那么剩下的结点地址应该全是NULL。

如果不是完全二叉树，那么队出到NULL是，跳出循环，队列中肯定还有不为NULL的地址。

bool TreeComplete(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	//先让队列进一个数据才能循环起来
	QueuePush(&q, root);
	while (!QueueEmpty(&q))
	{
		BTNode* head = QueueFront(&q);
		QueuePop(&q);
			//删除根结点地址在入它的孩子
		if (head != NULL)
		{
			QueuePush(&q, head->left);
			QueuePush(&q, head->right);
		}
		else	//队出空则跳出循环
		{
			break;
		}
	}

	while (!QueueEmpty(&q))
	{
		if (QueueFront(&q))
		{
			//进到这说明地址不是NULL
			QueueDestroy(&q);
			return false;
		}
		QueuePop(&q);
	}
	QueueDestroy(&q);
	return true;
}

二、 力扣相关OJ巩固基础

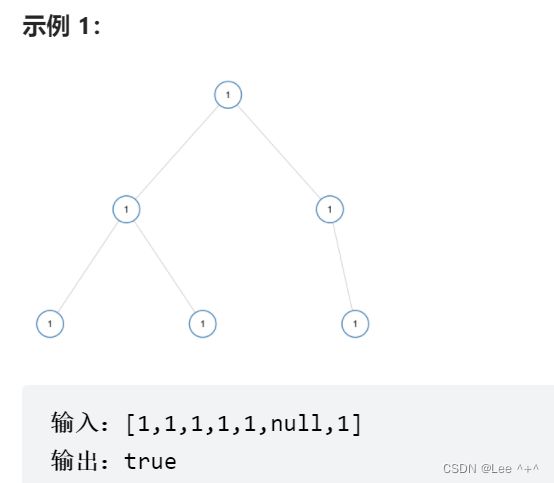
1 单值二叉树

（1）题目入口

965. 单值二叉树

（2）思路+代码

  若一棵树是当值二叉树，那么所有结点值相等，因为树的本质的是递归的，我们只需要比一组根和左右结点的值是否相等就行，再递归往下进行就行。

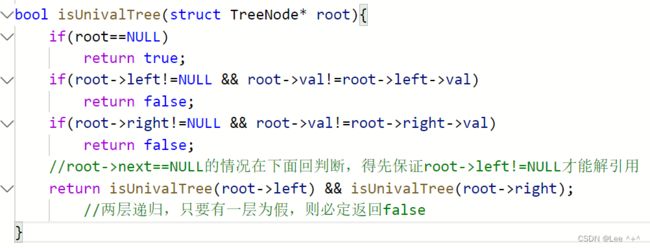
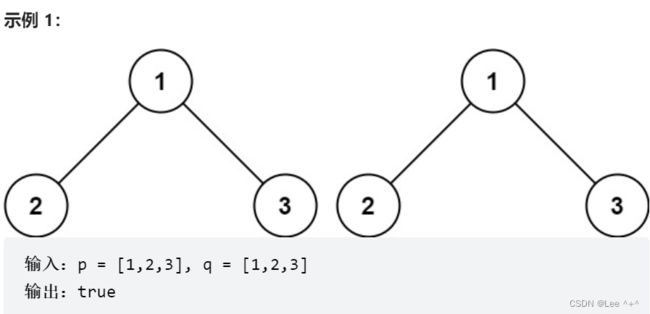
2 相同的树

（1）题目入口

100. 相同的树

（2）思路加代码

  和单值二叉树一样，我们先比较根左右结点再递归往下比较。

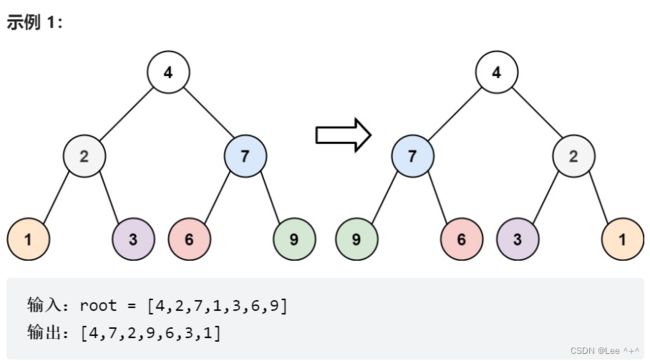
3 翻转二叉树

（1）题目入口

226. 翻转二叉树

（2）思路加代码

  翻转一颗树，我们可以从上往下翻转，以可以从上往下翻转，一样是根的左右的孩子翻转，再递归依次翻转。个人觉得还是从上往下翻转层次思路更加清晰一些。

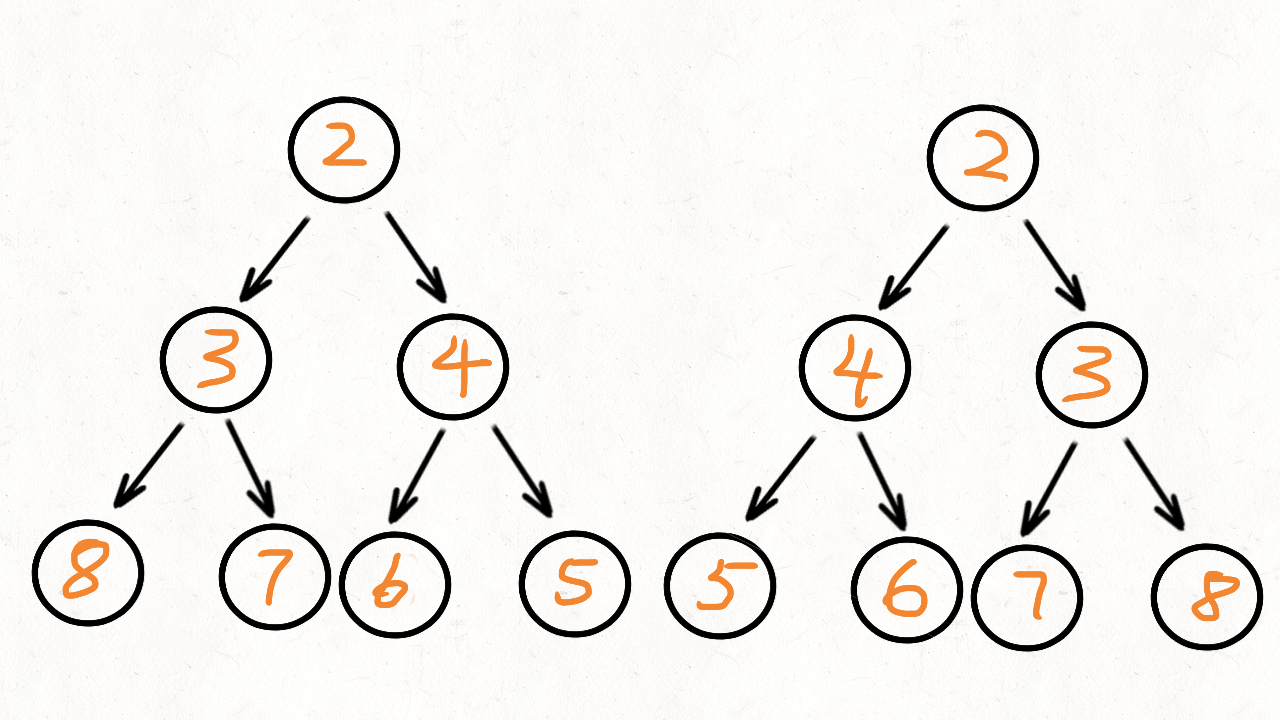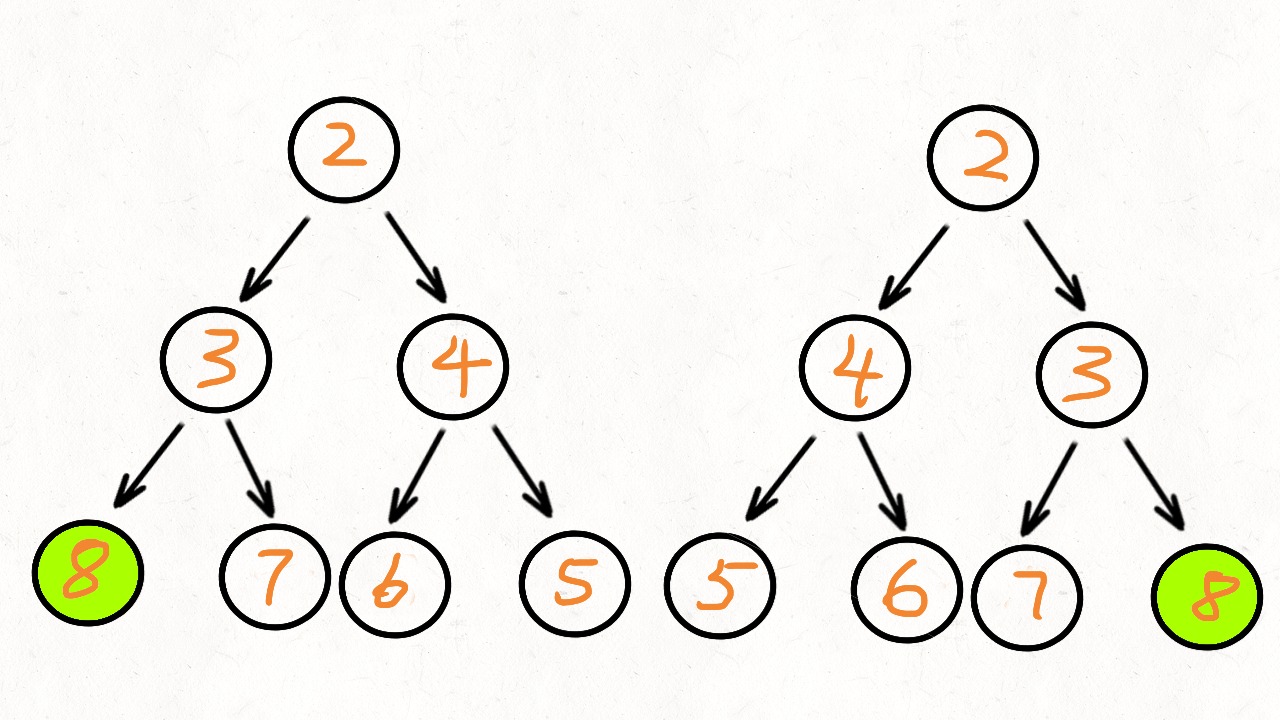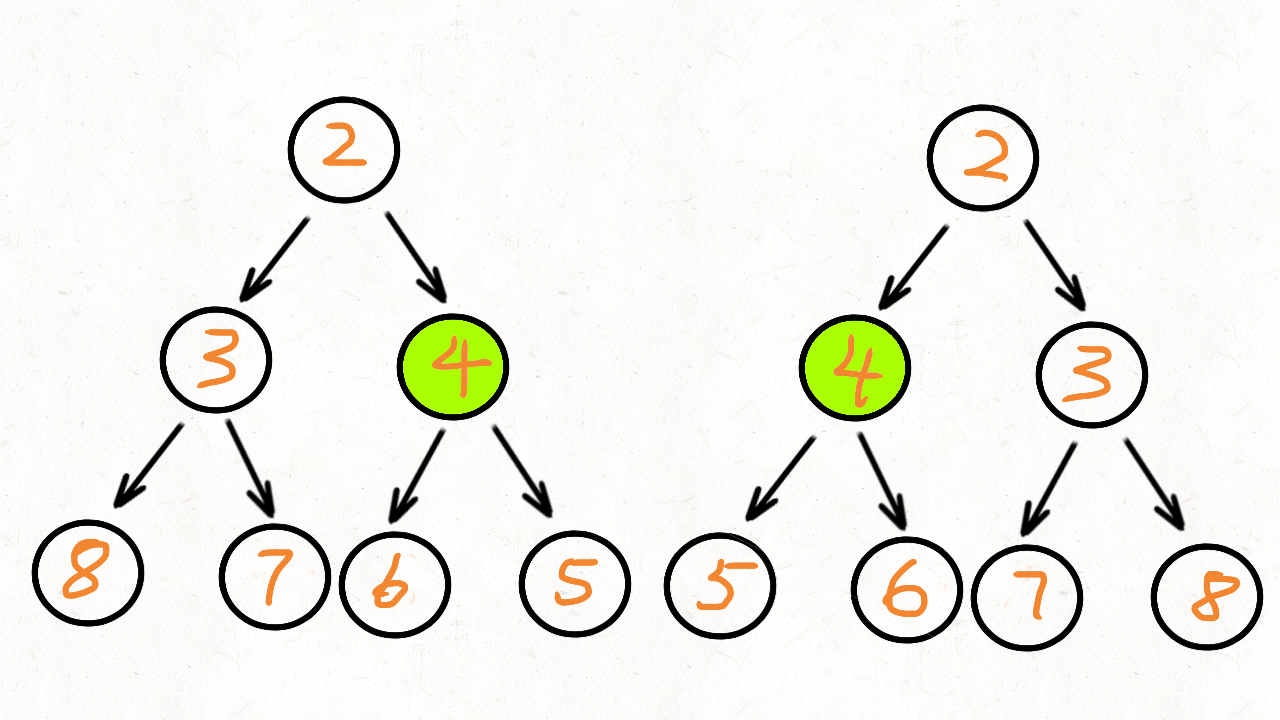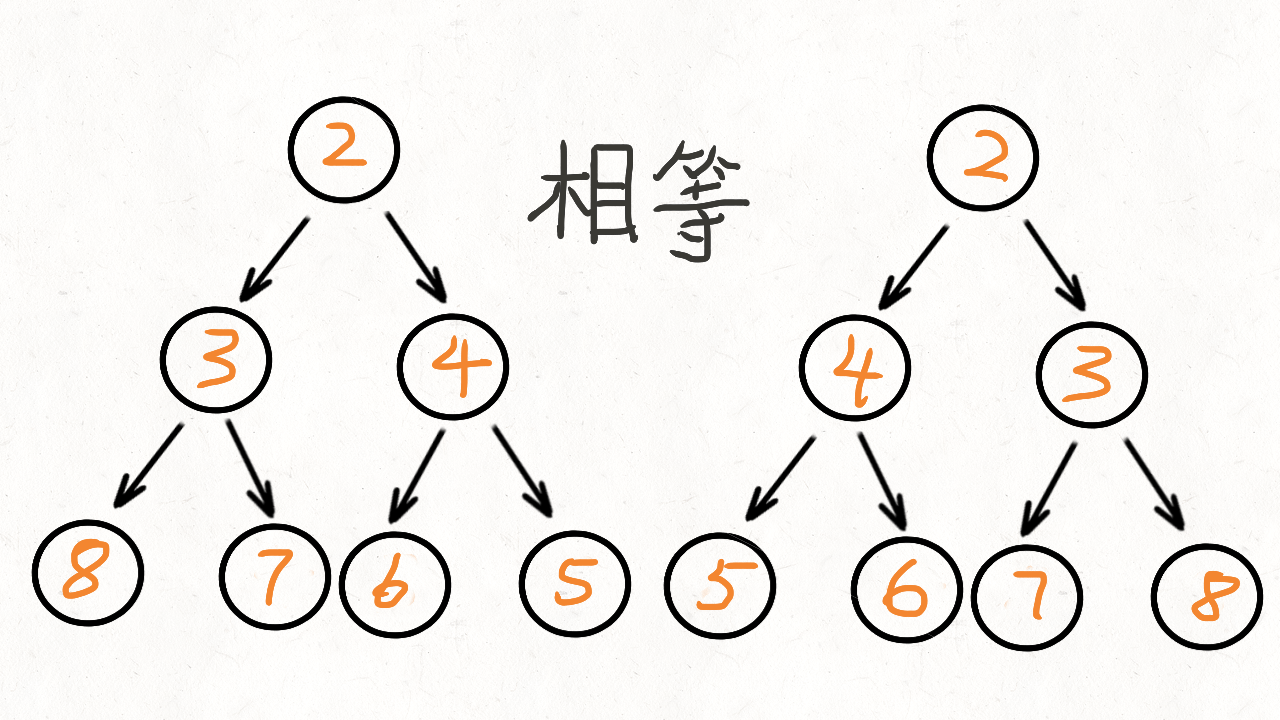
4 、对称二叉树

（1）题目入口

101. 对称二叉树

（2）思路加代码

  有了上面相同的树题目经验，那个题是两颗树同时往一个方向走进行比较。而对称二叉树我们把一颗树看成两颗树，自己调用自己，一颗树往左则另外一颗树往其反方向走便能判断出其是不是对称的。

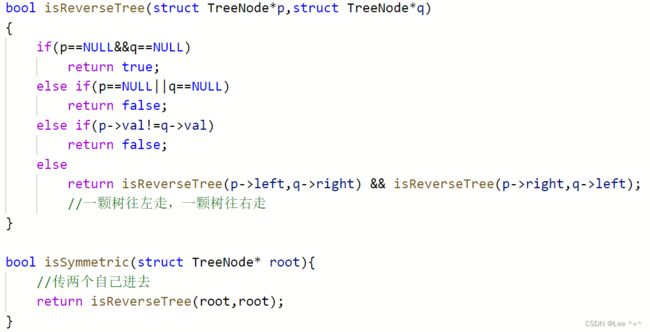
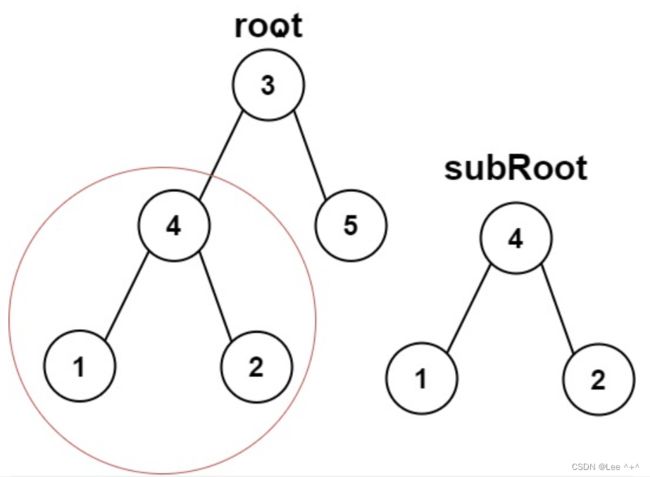
5 另一棵树的子树

（1）题目入口

572. 另一棵树的子树

（2）思路加代码

  写了前面单值二叉树后，这个题思路差不多。先从根开始比较，不是再比左右子树。递归进行，这里只需要调用判断相同的树这个辅助函数就行，也就是递归嵌套了一层递归。

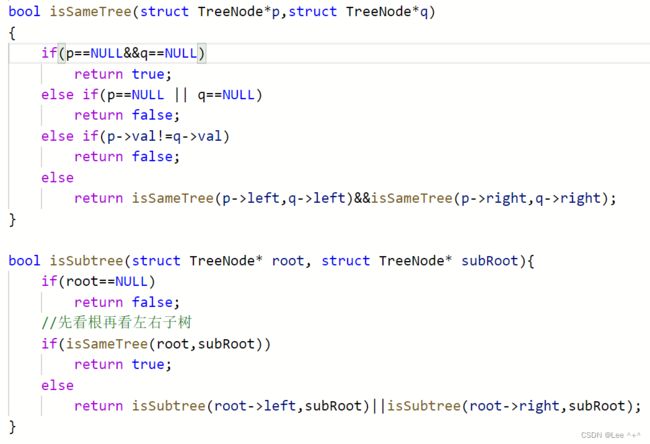
三、总结

  这些知识还在初阶的二叉树知识，基础巩固好了以后学复杂的二叉树知识也会轻松不少，期待下一篇博客见面。