【数据结构与算法】two X 树的遍历以及功能实现
个人主页:Dream_Chaser~
✨✨专栏:http://t.csdn.cn/oXkBa
⛳⛳本篇内容:c语言数据结构--二叉树的遍历以及功能实现
目录
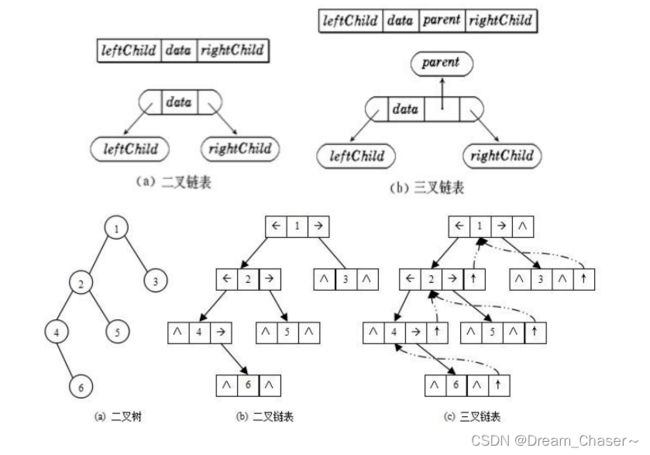
一.链式二叉树存储的概念
二.链式二叉树结构的实现
2.1 前置说明
2.2二叉树的遍历
前序遍历(Preorder Traversal)
中序遍历(Inorder Traversal)
后续遍历(Postorder Traversal)
层序遍历(LevelOrder)
2.3二叉树功能的实现
二叉树结构定义(struct BinaryTreeNode)
二叉树节点的创建(CreatBinaryTree)
二叉树的前序遍历函数(PrevOrder)
二叉树的中序遍历函数(InOrder)
二叉树的后序遍历函数(PostOrder)
统计二叉树节点个数(BTreeSize)
求出叶子节点的数量(BTreeLeafSize)
求二叉树的高度(BTreeHeight)
二叉树第k层节点个数(BTreeLevelKSize)
二叉树查找值为x的节点(BTreeFind)
二叉树的层序遍历(LevelOrder)
判断一棵树是否为完全二叉树(BinaryTreeComplete)
一.链式二叉树存储的概念
二.链式二叉树结构的实现
2.1 前置说明
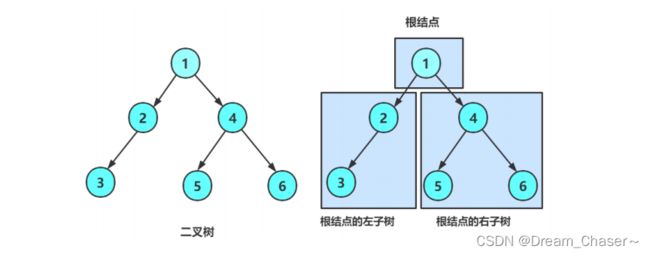
在学习二叉树的基本操作前,需先要创建一棵二叉树,然后才能学习其相关的基本操作。由于现在大家对二叉树结构掌握还不够深入,为了降低大家学习成本,此处手动快速创建一棵简单的二叉树,快速进入二叉树操作学习,等二叉树结构了解的差不多时,我们反过头再来研究二叉树真正的创建方式。
typedef int BTDataType;
typedef struct BinaryTreeNode
{
BTDataType data;
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
}BTNode;
BTNode* BuyNode(BTDataType x)
{
BTNode* node = (BTNode*)malloc(sizeof(BTNode));
if (node == NULL)
{
perror("malloc fail");
return NULL;
}
node->data = x;
node->left = NULL;
node->right = NULL;
return node;
}
BTNode* CreatBinaryTree()
{
BTNode* node1 = BuyNode(1);
BTNode* node2 = BuyNode(2);
BTNode* node3 = BuyNode(3);
BTNode* node4 = BuyNode(4);
BTNode* node5 = BuyNode(5);
BTNode* node6 = BuyNode(6);
node1->left = node2;
node1->right = node4;
node2->left = node3;
node4->left = node5;
node4->right = node6;
return node1;
}后续遍历(Postorder Traversal)
层序遍历(LevelOrder)
2.3二叉树功能的实现
二叉树结构定义(struct BinaryTreeNode)
代码实现:
typedef int BTDataType;
typedef struct BinaryTreeNode
{
BTDataType data;
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
}BTNode;二叉树节点的创建(CreatBinaryTree)
BTNode* BuyNode(BTDataType x)//树中一个节点的创建
{
BTNode* node = (BTNode*)malloc(sizeof(BTNode));
if (node == NULL)
{
perror("malloc fail");
return NULL;
}
node->data = x;
node->left = NULL;
node->right = NULL;
return node;
}
BTNode* CreatBinaryTree()//树的构造
{
BTNode* node1 = BuyNode(1);
BTNode* node2 = BuyNode(2);
BTNode* node3 = BuyNode(3);
BTNode* node4 = BuyNode(4);
BTNode* node5 = BuyNode(5);
BTNode* node6 = BuyNode(6);
node1->left = node2;
node1->right = node4;
node2->left = node3;
node4->left = node5;
node4->right = node6;
return node1;
}
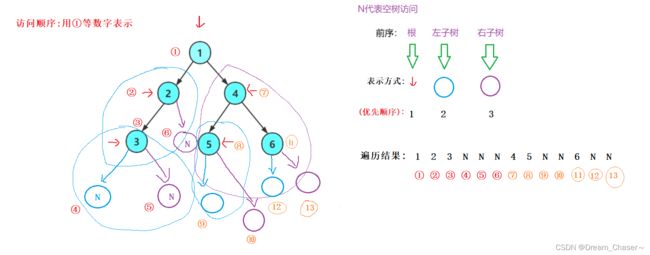
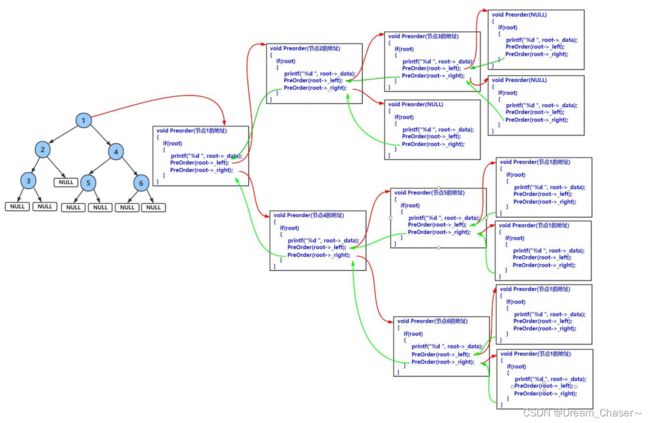
二叉树的前序遍历函数(PrevOrder)
递归不可能一直调用函数,因为这个过程一直在创建栈帧,即使栈再大,也会栈溢出。所以肯定会回归,回归的本质就是销毁栈帧。
递归是由两个部分构成:
1.子问题
2.返回条件
图解:
代码实现:
void PrevOrder(BTNode* root)
{
if (root == NULL)
{
printf("N ");
return;
}
printf("%d ", root->data);
PrevOrder(root->left);
PrevOrder(root->right);
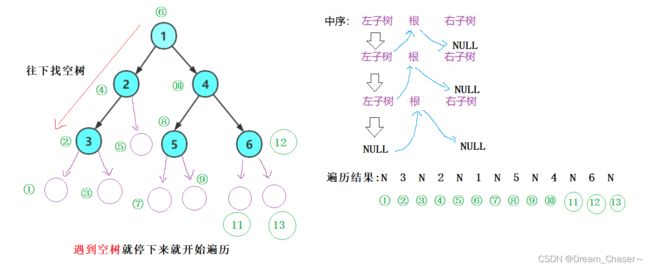
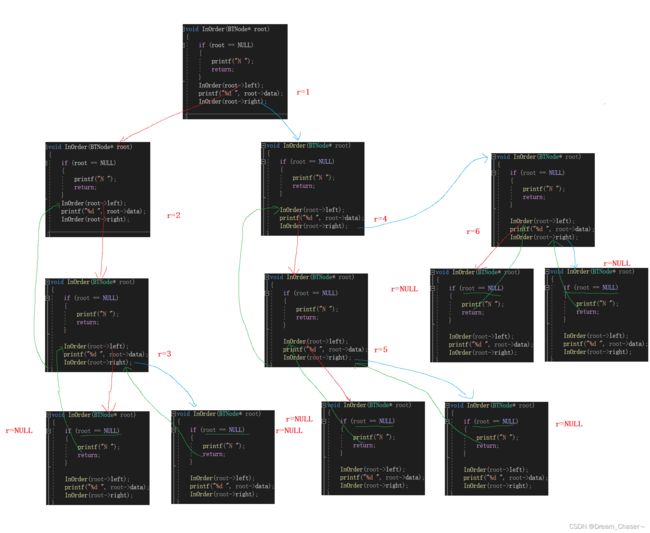
}二叉树的中序遍历函数(InOrder)
绘图:
void InOrder(BTNode* root)
{
if (root == NULL)
{
printf("N ");
return;
}
InOrder(root->left);
printf("%d ", root->data);
InOrder(root->right);
}
二叉树的后序遍历函数(PostOrder)
跟前中序的思路相差不大,这里就不绘图了。
代码实现:
void PostOrder(BTNode* root)
{
if (root == NULL)
{
printf("N ");
return;
}
PostOrder(root->left);
PostOrder(root->right);
printf("%d ", root->data);
}统计二叉树节点个数(BTreeSize)
画出递归展开图:
int BTreeSize(BTNode* root)
{
//写法一
if (root == NULL)
return 0;
return BTreeSize(root->left) + BTreeSize(root->right) + 1;
//写法二
return root == NULL ? 0 : BTreeSize(root->left) + BTreeSize(root->right) + 1;
}求出叶子节点的数量(BTreeLeafSize)
进入函数首先判断根节点是否为空,为空就直接返回0,说明树为空,直接返回叶子节点数量为0。
接下来,检查当前的节点是叶子节点还是分支节点,若代码检查当前节点是否为叶子节点,即该节点的左子节点和右子节点都为空。如果是叶子节点,返回叶子节点数量为1。
如果当前节点为分支节点,则继续调用该函数,计算左子树和右子树的叶子节点数量,并将它们相加,得到当前节点为根的子树的叶子节点数量。
最后,函数返回左子树和右子树叶子节点数量的和,即整个二叉树的叶子节点数量。
int BTreeLeafSize(BTNode* root)//接受一个指向二叉树节点的指针root作为参数
{
if (root == NULL)//代码检查根节点是否为空
{
return 0;
}
if ( root->left==NULL &&root->right==NULL)
{
return 1;
}
return BTreeLeafSize(root->left) + BTreeLeafSize(root->right);
}求二叉树的高度(BTreeHeight)
先比较一下以下的哪种代码更优:
方案一:
在递归调用BTreeHeight函数之后,并没有对返回值进行保存和比较,而是直接返回了当前节点的左子树和右子树的高度中较大的一个加1。这样的实现虽然能够得到正确的结果,但是效率较低。因为在计算左子树的高度和右子树的高度时,每次都会重复递归调用 BTreeHeight函数
int BTreeHeight(BTNode* root)
{
if (root == NULL)
{
return 0;
}
return BTreeHeight(root->left) > BTreeHeight(root->right) ?
BTreeHeight(root->left) + 1 : BTreeHeight(root->right) + 1;
}为了更好地理解方案一的解释,这里写出一个不用三目运算符,但是等价于上述代码的代码
画图理解:
这里其实用到的是分治算法,通常分为三个步骤:
分解(Divide):将原问题划分为若干个规模较小的子问题。这一步通常在递归的过程中进行,直到问题足够简单,可以直接求解。
解决(Conquer):递归地解决子问题。对于每个子问题,如果它的规模足够小,可以直接求解;否则,继续递归地将子问题划分为更小的子问题。
合并(Combine):将子问题的解合并得到原问题的解。这一步通常在递归的回溯过程中进行。
代码实现:
int BTreeHeight(BTNode* root)
{
if (root == NULL)
{
return 0;
}
int h = 0;
if (BTreeHeight(root->left) > BTreeHeight(root->right))
{
h = BTreeHeight(root->left) + 1;
}
else
{
h = BTreeHeight(root->right) + 1;
}
return h;
}力扣执行:
方案二:
使用了两个变量leftHeight和rightHeight分别保存了左子树和右子树的高度。通过递归调用BTreeHeight函数分别计算左子树和右子树的高度,并将结果保存在这两个变量中。然后比较leftHeight和rightHeight的值,将较大值加1作为当前节点的高度返回。这样的实现避免了重复计算,提高了效率。
int BTreeHeight(BTNode* root)
{
if (root == NULL)
{
return 0;
}
int leftHeight = BTreeHeight(root->left);
int rightHeight = BTreeHeight(root->right);
return leftHeight > rightHeight ? leftHeight + 1 : rightHeight+ 1;
}力扣执行:
二叉树第k层节点个数(BTreeLevelKSize)
子问题:
转换成左子树的第k-1层和右子树的右子树的第k-1层
结束条件:
- k == 1且节点不为空
- 节点为空
代码实现:
int BTreeLevelKSize(BTNode* root, int k)
{
assert(k > 0);
if (root == NULL)
return 0;
if (k == 1)
return 1;
return BTreeLevelKSize(root->left, k - 1)
+ BTreeLevelKSize(root->right, k - 1);
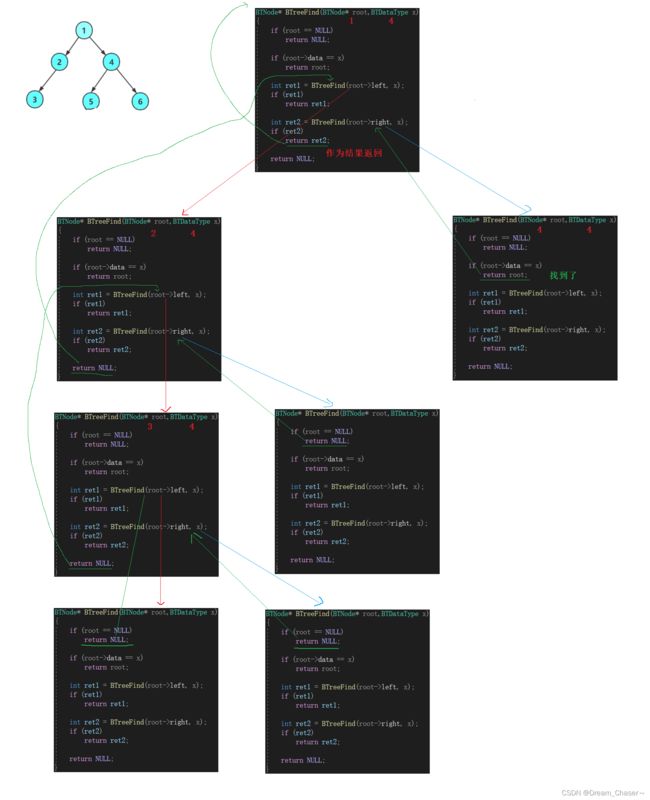
}二叉树查找值为x的节点(BTreeFind)
思路:就如果根节点为空,直接返回NULL,如果找到了就返回x这个节点的地址。
从根节点开始遍历,先从左子树开始找,继续循环上述思路,如果节点不为NULL,但是节点不为x,那也是返回NULL,注意这个NULL是返回上一层的,谁调用它就返回给此函数。之后找右子树,也是一样的思路。
左子树整体找完之后,从右子树整体开始找,重复上述过程。特别强调一个点,return返回的时候不会return到最外层,一定是逐层逐层返回的,没有跳跃的一个过程。
画出递归展开图:
代码实现:
BTNode* BTreeFind(BTNode* root,BTDataType x)
{
if (root == NULL)
return NULL;
if (root->data == x)
return root;
int ret1 = BTreeFind(root->left, x);
if (ret1)
return ret1;
int ret2 = BTreeFind(root->right, x);
if (ret2)
return ret2;
return NULL;
}
二叉树的层序遍历(LevelOrder)
层序遍历是用队列实现的,所以要使用队列的结构体,以下的结构体都要用到
typedef struct BTNode* QDataType;//注意这个地方的类型
typedef struct QueueNode
{
QDataType data;
struct QueueNode* next;
}QNode;
typedef struct Queue
{
QNode* phead;
QNode* ptail;
int size;
}Queue;//表示队列整体,一个是出数据,一个是入数据.
typedef int BTDataType;
typedef struct BinaryTreeNode
{
BTDataType data;
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
}BTNode;
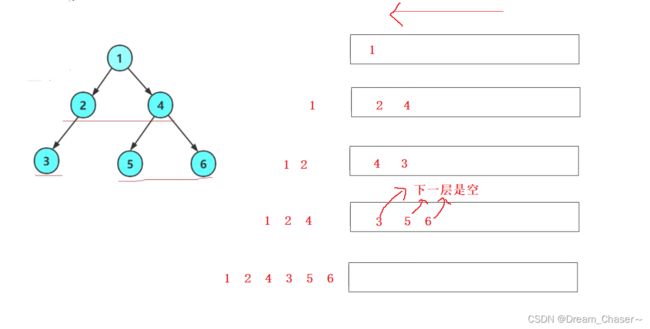
画处解析图:
队列:先进先出
核心思路:上一层出时带下一层进队列
解析: 其实就是由原来的队列里面data的int类型,变成了struct BTreeNode* 类型的指针,指向了这个数节点。
代码实现:
void LevelOrder(BTNode* root)
{
Queue q;//在函数内部,定义了一个队列q,并通过调用QueueInit函数对队列进行初始化。
QueueInit(&q);
//如果根节点root不为空,将根节点入队,即调用QueuePush函数将root指针插入到队列q中。
if (root)
QueuePush(&q,root);
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);//首先通过调用QueueFront函数获取队列q的队首元素,并将其赋值给指针变量front
QueuePop(&q);//调用QueuePop函数将队首元素出队
printf("%d ", front->data);//通过printf函数打印front指向的节点的数据值
//如果front的左子节点不为空,将左子节点入队,
//即调用QueuePush函数将front->left指针插入到队列q中
if (front->left)
QueuePush(&q, front->left);//后面这个参数是一个值,不是地址
//如果front的右子节点不为空,将右子节点入队,
//即调用QueuePush函数将front->right指针插入到队列q中。
if (front->right)
QueuePush(&q, front->right);//后面这个参数是一个值,不是地址
//循环体内的操作完成后,继续下一次循环,直到队列q为空。
}
//最后,打印换行符表示层序遍历结束,
//并调用QueueDestroy函数销毁队列q,释放内存。
printf("\n");
QueueDestroy(&q);
}
二叉树的销毁(BTDestroy)
解析:要先判断根节点本身是否为空,为空就不销毁,返回。
销毁是用到后序遍历的,因为中途删掉了根节点,那么左右指针就找不到了,所以后序遍历适合实现二叉树的销毁。
画图:
void BTDestroy(BTNode* root)
{
if (root == NULL)
{
return NULL;
}
BTDestroy(root->left);
BTDestroy(root->right);
free(root);
}判断一棵树是否为完全二叉树(BinaryTreeComplete)
非完全二叉树
完全二叉树
思路一样的就不画动图了,只要前面遇到一次空,立即跳出循环,停止插入元素,然后检查后面的元素是否为空,后面全是空就是完全二叉树了。
以下这个二叉树就不是完全二叉树了
代码实现:
bool BTreeComplete(BTNode* root)
{
Queue q;
QueueInit(&q);
if (root)
QueuePush(&q,root);
while (!QueueEmpty(&q))//遍历树直到找到第一个空节点
{
BTNode* front= QueueFront(&q);
QueuePop(&q);
//遇到空就跳出
if (front == NULL)
{
break;
}
QueuePush(&q, front->left);
QueuePush(&q, front->right);
}
// 检查后面的节点有没有非空
// 有非空,不是完全二叉树
while (!QueueEmpty(&q))//由于中途遇到空,所以跳出循环,这次循环是为了检查后面元素是否为空
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
if (front)
{
QueueDestroy(&q);
return false;
}
}
QueueDestroy(&q);
return true;
}
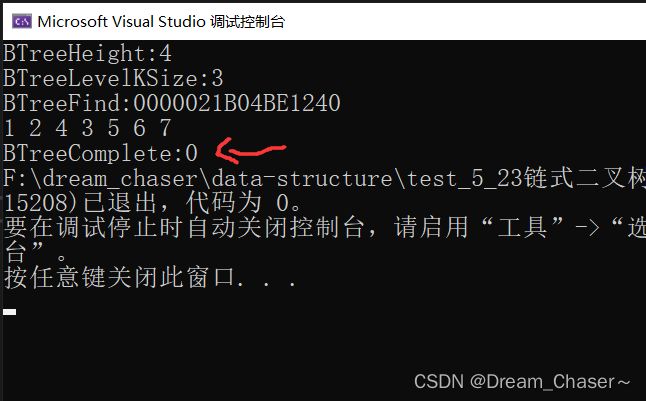
执行:
本篇到此结束,感谢来访!