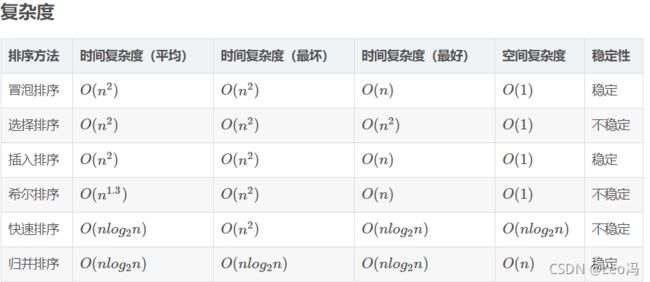
排序算法思路及时间复杂度
1.原地排序算法的含义?
指空间复杂度为O(1)的排序算法
例如冒泡排序,在这个过程中我们只开辟了一个临时存储空间来存放交换时的数据
在这些排序中不用太过关注写的代码,着重传递思想
1.冒泡排序
比较相邻的两个数,较大的放后面,较小的放前面(先排好的是最大值)
时间复杂度:O(n^2) 空间复杂度O(1)
是稳定的
2.选择排序
每次从待排序列中选出一个最小值,然后放在序列的起始位置,直到全部待排数据排完即可
(先排好的是最小值)
时间复杂度:O(n^2) 空间复杂度O(1)
优化:
实际上,我们可以一趟选出两个值,一个最大值一个最小值,
然后将其放在序列开头和末尾,这样可以使选择排序的效率快一倍
不稳定的排序算法(每次比较都是跳跃性的,比较两个相同数据的相同位置明显发生变化)
3.直接插入排序
假设之前的数据已经有序,将后面的数据找到合适的位置插入
(一开始认为第一个元素是有序的,依次将其后面的元素插入到这个有序序列中来,直到整个序列有序为止)
时间复杂度:O(n^2) 空间复杂度O(1)
是稳定的
(1).普通插入排序的时间复杂度最坏情况下为O(N^2),此时待排序列为逆序,或者说接近逆序。
(2).普通插入排序的时间复杂度最好情况下为O(N),此时待排序列为升序,或者说接近升序。
4.希尔排序(又名缩小增量法)
(比之前的三个排序算法首次打破n^2时间复杂度)
(为插入排序的延申)
经过对之前直接插入排序复杂度的分析,如果在直接排序之前加一次预排序
使待排序列接近有序然后再进行一次直接插入排序,复杂度就降下来了
思想:1.先选定一个gap为第一增量,然后将所有距离为gap的元素分在同一组,并对每一组的元素进行直接插入排序。
然后再取一个比第一增量小的整数作为第二增量,重复上述操作…
2.当增量的大小减到1时,就相当于整个序列被分到一组,进行一次直接插入排序,排序完成。
问题:为什么要让gap由大到小呢?
answer:gap越大,数据挪动得越快;gap越小,数据挪动得越慢。
前期让gap较大,可以让数据更快得移动到自己对应的位置附近,减少挪动次数。
注:一般情况下,取序列的一半作为增量,然后依次减半,直到增量为1(也可自己设置)
时间复杂度:O(nlogn) ~ O(n^2) 和选的增量有关 空间复杂度O(1)
平均时间复杂度:O(n^1.3)
不稳定的
5.二分查找
折中查
!前提:这个序列必须为有序序列
时间复杂度:O(nlogn)
6.快速排序
选取一个基准值key,经过一趟排序后(Hoare/前后指针)使基准值左边的都比它小
基准值右边都是比基准值大的数,这个时候左右序列重复该过程,直到所有元素都排列在相应位置上。
如何按照基准值将待排序列分为两子序列
1.Hoare版本
2.挖坑法(略)
3.前后指针法
Hoare版本的单趟排序的基本步骤如下:
1、选出一个key,一般是最左边或是最右边的。
2、定义一个L和一个R,L从左向右走,R从右向左走。
(需要注意的是:若选择最左边的数据作为key,则需要R先走;若选择最右边的数据作为key,则需要L先走)。
3、在走的过程中,若R遇到小于key的数,则停下,
L开始走,直到L遇到一个大于key的数时,将L和R的内容交换,
R再次开始走,如此进行下去,直到L和R最终相遇,此时将相遇点的内容与key交换即可。
(选取最左边的值作为key)
经过一次单趟排序,最终使得key左边的数据全部都小于key,key右边的数据全部都大于key。
然后我们在将key的左序列和右序列再次进行这种单趟排序,如此反复操作下去,
直到左右序列只有一个数据,或是左右序列不存在时,便停止操作,因为这种序列可以认为是有序的。
前后指针法的单趟排序的基本步骤如下:
1、选出一个key,一般是最左边或是最右边的。
2、起始时,prev指针指向序列开头,cur指针指向prev+1。
3、若cur指向的内容小于key,则prev先向后移动一位,然后交换prev和cur指针指向的内容,然后cur指针++;若cur指向的内容大于key,则cur指针直接++。如此进行下去,直到cur指针越界,此时将key和prev指针指向的内容交换即可。
经过一次单趟排序,最终也能使得key左边的数据全部都小于key,key右边的数据全部都大于key。
然后也还是将key的左序列和右序列再次进行这种单趟排序,如此反复操作下去,直到左右序列只有一个数据,或是左右序列不存在时,便停止操作。
快速排序的非递归算法基本思路:
1、先将待排序列的第一个元素的下标和最后一个元素的下标入栈。
2、当栈不为空时,读取栈中的信息(一次读取两个:一个是L,另一个是R),然后调用某一版本的单趟排序,排完后获得了key的下标,然后判断key的左序列和右序列是否还需要排序,若还需要排序,就将相应序列的L和R入栈;若不需排序了(序列只有一个元素或是不存在),就不需要将该序列的信息入栈。
3、反复执行步骤2,直到栈为空为止。
时间复杂度:O(nlogn)
是不稳定的
快速排序的两个优化
1.三数取中
理想情况下单趟排完序后key值在中间,如果每次key值排完都在最左边
这种情况下时间复杂度退化为o(n^2)所以为了避免这种情况出现了三数取中
最左边的数,最右边的数,最中间的数,取这三个数居中的为key值
2.小区间优化
随着递归的深入,递归的次数以2倍的方式快速增长
为了减少后几次递归,可以设置如果序列小于某个数的话就不再进行快速排序,转而使用其它种类的排序
7.归并排序
归并排序是采用分治法的一个非常典型的应用。
其基本思想是:将已有序的子序合并,从而得到完全有序的序列,即先使每个子序有序,再使子序列段间有序。
那么如何得到有序的子序列呢?
当序列分解到只有一个元素或是没有元素时,就可以认为是有序了,这时分解就结束了,开始合并:
时间复杂度:O(nlogn) 空间复杂度O(n)