数据结构之“初窥门径”

目录

前言：

一，数据结构起源

二，基本概念和术语

2.1数据

2.2数据元素

2.3数据项

2.4数据对象

2.5数据结构

三，逻辑结构与物理结构

3.1逻辑结构

3.1.1集合结构

3.1.2线性结构

3.1.3树形结构

3.1.4图形结构

3.2物理结构

3.2.1顺序存储结构

3.2.2链式存储结构

四，数据类型

4.1数据类型的定义

4.2抽象数据类型

---

前言：

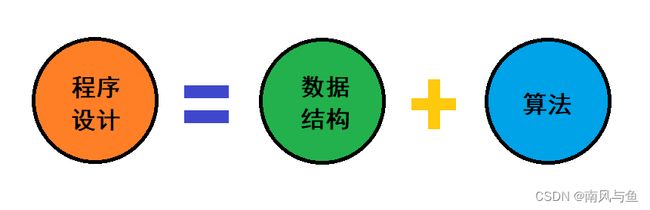
在计算机科学中，数据结构是一种用于组织和存储数据的方式。它是计算机程序设计的基础，对于解决问题和提高代码效率至关重要。数据结构可以看作是一种容器，它可以存储和操作数据。不同的数据结构有不同的特点和应用场景。

学习数据结构的目的是为了更好的理解和处理数据，通过选择合适的数据结构我们可以提高程序的运行效率，并实现更高效的算法。同时，数据结构也是算法设计和分析的基础，它们相互依存，相互影响。

很喜欢《大话数据结构》这本书的开场白：“如果你交给某人一个程序，你将折磨他一整天；如果你教某人如何编写程序，你将折磨他一辈子”，哈哈哈。

---

一，数据结构起源

早期人们都把计算机理解为数值计算工具，就是感觉计算机当然是用来计算的，所以计算机解决问题，应该是先从具体问题中抽象出一个适当的数据模型，设计出一个解此数据模型的算法，然后再编写程序，得到一个实际的软件。

可现实中，我们更多的不是解决数值计算的问题，而是需要一些更科学更有效的手段（比如表，树和图等数据结构）的帮助，才能更好的处理问题。所以：

数据结构是一门研究非数值计算的程序设计问题中的操作对象，以及它们之间的关系和操作等相关问题的学科。

1968年，美国的高德纳 （Donald E. Knuth）教授在其所写的 《计算机程序设计艺术》第一卷《基本算法》中，较系统地阐述了数据的逻辑结构和存储结构及其操作，开创了数据结构的课程体系。同年，“数据结构〞作为一门独立的课程，在计算机科学的学位课程中开始出现。也就是说，那之后计算机相关专业的学生开始接受 “数据结构”的“折磨”——其实应该是享受才对。

之后，20世纪70年代初，出现了大型程序，软件也开始相对独立，结构程序设计成为程序设计方法学的主要内容，人们越来越重视“数据结构”，认为程序设计的实质是对确定的问题选择一种好的结构，加上设计一种好的算法。可见，数据结构在程序设计当中占据了重要的地位。

二，基本概念和术语

说到数据结构，我们得先来谈谈什么叫数据。

正所谓“巧妇难为无米之炊”，这个“米”就是数据。

2.1数据

数据是描述客观事物的符号，是计算机中可以操作的对象，是能被计算机识别，并输入给计算机处理的符号集合。数据不仅仅包括整形，实型等数据类型，还包括字符及声音，图像，视频等非数值类型。

比如我们现在常用的搜索引擎，一般会有网页，图片，音频，视频等分类。图片是图像数据，音频当然就是声音数据，视频就不用说了，而网页其实指的就是全部数据的搜索，包括最重要的数字和字符等文字数据。

也就是说，我们这里说的数据，其实就是符号，而且这些符号必须具备两个前提：

• 可以输入到计算机中。
• 能被计算机程序处理。

对于整型，实型等数值类型，可以进行数值计算。

对于字符数据类型，就需要进行非数值的处理。而声音，图像，视频等其实是可以通过编码的手段变成字符数据来处理的。

2.2数据元素

数据元素是组成数据的，有一定意义的基本单位，在计算机中通常作为整体处理，也被称为记录。

比如，在人类中，什么是数据元素呀？当然是人了。

畜禽类呢？牛，马，羊，猪，鸡，鸭等动物当然就是畜禽类的数据元素。

2.3数据项

数据项：一个数据元素可以由若干个数据项组成。

比如人这样的数据元素，可以由眼睛，耳朵，嘴巴，鼻子，手，脚这些数据项，也可以由姓名，年龄，性别，家庭地址，联系电话，邮政编码等数据项，具体有哪些数据项，要由你做的系统来决定。

数据项是数据不可分割的最小单位。

之所以将数据项定义为最小单位，是因为这样有助于帮我们更好的解决问题。但真正讨论问题时，数据元素才是数据结构中建立数据模型的着眼点，就像我们讨论一部电影时，是讨论这部电影角色这样的“数据元素”，而不是针对这个角色的姓名或者年龄这样的“数据项”去研究分析。

2.4数据对象

数据对象是性质相同的数据元素的集合，是数据的子集。

什么叫性质相同呢，是指数据元素具有相同数量和类型的数据项，比如，人都有姓名，生日，性别等相同的数据项。

2.5数据结构

结构，简单的理解就是关系，比如分子结构，就是说组成分子的原子之间的排列方式。严格点说，结构是指各个组成部分相互搭配和排列的方式。在现实世界中，不同数据元素之间不是独立的，而是存在特定的关系，我们将这些关系称为结构。那数据结构是什么？

数据结构：是相互之间存在一种或多种特定关系的数据元素的集合。

三，逻辑结构与物理结构

按照视点的不同，我们把数据结构分为逻辑结构和物理结构。

3.1逻辑结构

逻辑结构是指数据对象中数据元素之间的相互关系。

它分为以下四种：

3.1.1集合结构

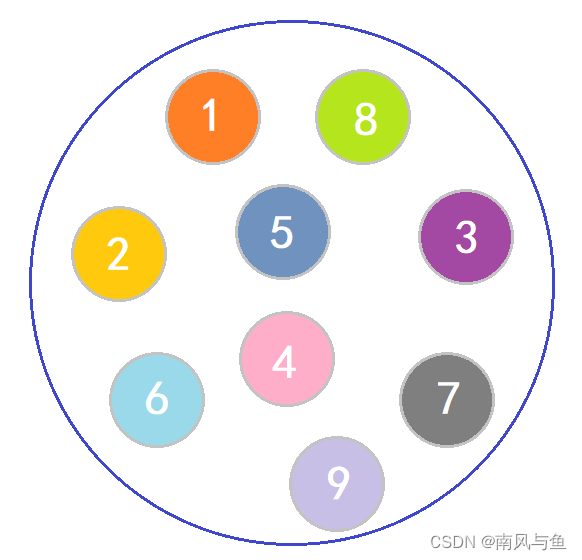
集合结构：集合结构中的数据元素除了同属于一个集合外，它们之间没有其他关系。各个数据元素是“平等”的，它们的共同属性是“同属于一个集合”。数据结构中的集合关系就类似于数学中的集合。

3.1.2线性结构

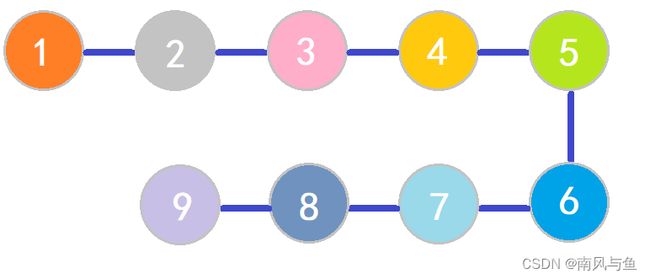
线性结构：线性结构中的数据元素之间是一对一的关系。

3.1.3树形结构

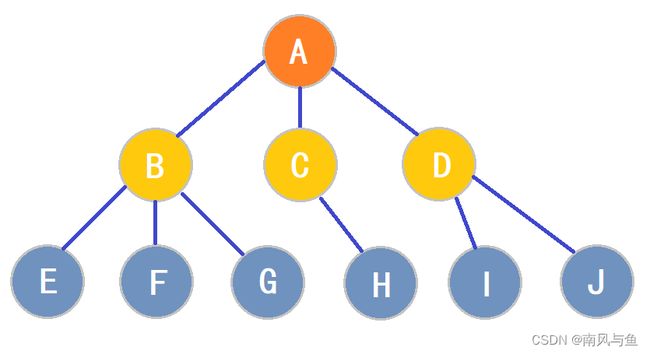
树形结构：树形结构中的数据元素之间存在一种一对多的层次关系。

3.1.4图形结构

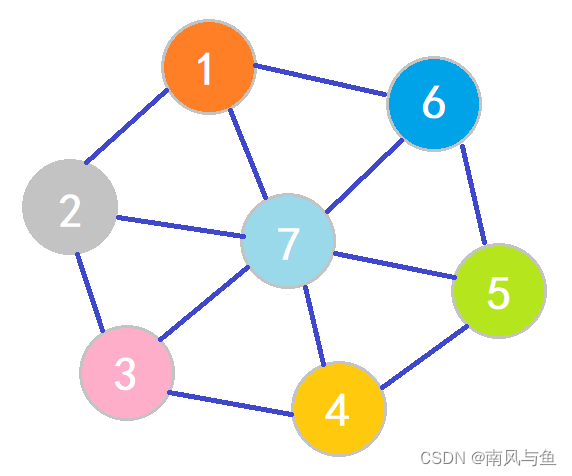
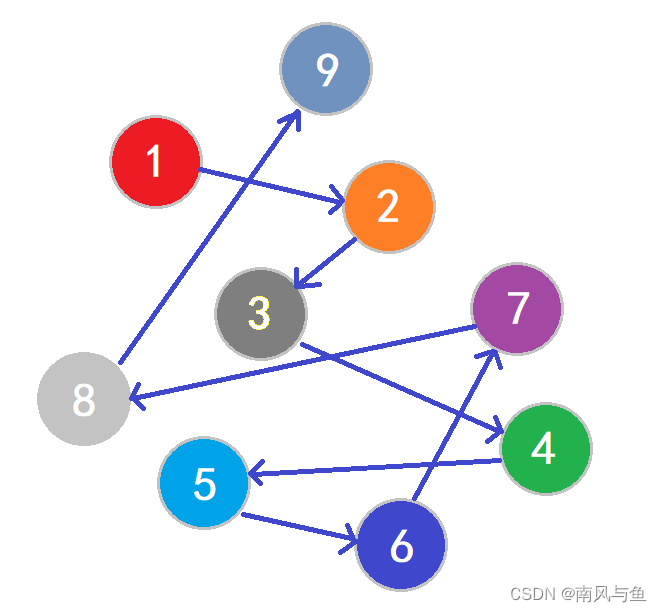
图形结构：图形结构的数据元素是多对多的关系。

我们在用示意图表示数据的逻辑结构时，要注意两点：

• 将每一个数据元素看作一个结点，用圆圈表示。
• 元素之间的逻辑关系用结点之间的连线表示，如果这个关系是有方向的，那么用带箭头的连线表示。 

3.2物理结构

物理结构：是指数据的逻辑结构在计算机中的存储形式。

数据是数据元素的集合，那么根据物理结构的定义，实际上就是如何把数据元素存储到计算机的存储器中。存储器主要是针对内存而言的，像硬盘，软盘，光盘等外部存储器的数据组织通常用文件结构来描述。

数据结构的存储结构形式有以下两种： 

3.2.1顺序存储结构

顺序存储结构：是把元素存放在地址连续的存储单元里，其数据间的逻辑关系和物理关系是一致的。

这种存储结构其实很简单，说白了，就是排队占位。大家都按顺序排好，每个人占一小段空间，大家谁也别插谁的队。我们之前学计算机语言时，数组就是这样的顺序存储结构。当你告诉计算机，你要建立一个有9个整型数据的数组时，计算机就在内存中找了片空地，按照一个整型所占位置的大小乘以9，开辟一段连续的空间，于是第一个数组数据就放在第一个位置，第二个数据放在第二个位置，这样依次摆放。如下图所示。

 

3.2.2链式存储结构

如果就是这么简单和有规律，一切就好办了。可实际上，总会有人插队，也会有人要上网所、有人会放弃排队。所以这个队伍当中会添加新成员，也有可能会去掉老元素，整个结构时刻都处于变化中。显然，面对这样要时常变化的结构，顺序存储是不科学的。那怎么办呢？

现在如银行、医院等地方，设置了排队系统，也就是每个人去了，先领一个号，等着叫号，叫到时去办理业务或看病。在等待的时候，你爱在哪在哪，可以坐着、站着或者走动，甚至出去逛一圈，只要及时回来就行。你关注的是前一个号有没有被叫到，叫到了，下一个就轮到你了。

链式存储结构：是把数据元素存放在任意的存储单元里，这组存储单元可以是连续的，也可以是不
连续的。数据元素的存储关系并不能反映其逻辑关系，因此需要用一个指针存放数据元素的地址，这样通过地址就可以找到相关联数据元素的位置。如图所示。
显然，链式存储就灵活多了，数据存在哪里不重要，只要有一个指针存放了相应的地址就能找到它了。

逻辑结构是面向问题的，而物理结构就是面向计算机的，其基本的目标就是将数据及其逻辑关系存储到计算机的内存中。 

四，数据类型

数据类型：是指一组性质相同的值的集合及定义在此集合上的一些操作的总称。

4.1数据类型的定义

数据类型是按照值的不同进行划分的。在高级语言中，每个变量、常量和表达式都有各自的取值范围。类型就用来说明变量或表达式的取值范国和所能进行的操作。

当年那些设计计算机语言的人，为什么会考虑到数据类型呢？

比如，大家都需要有房子住，也都希望房子越大越好。但显然，没有钱，考虑房子是没啥意义的。于是商品房就出现了各种各样的房型，有别墅的，有错层的，有单间的；有一百多平米的，也有几十平米的，甚至还有胶囊公寓----只有两平米的房间⋯这样就满足了不同人的需要。

同样，在计算机中，内存也不是无限大的，你要计算一个如1+1=2、3+5=8这样的整型数字的加减乘除运算，显然不需要开辟很大的适合小数甚至字符运算的内存空间。于是计算机的研究者们就考虑，要对数据进行分类，分出来多种数据类型。

在C语言中，按照取值的不同，数据类型可以分为两类：

 

比如，在C语言中变量声明int a，b，这就意味着，在给变量a和b赋值时不能超出int的取值范围，变量a和b之问的运算只能是int类型所允许的运算。

因为不同的计算机有不同的硬件系统，这就要求程序语言最终通过编译器或解释器转换成底层语言，如汇编语言甚至是通过机器语言的数据类型来实现的。可事实上，高级语言的编程者不管最终程序运行在什么计算机上，他的目的就是为了实现两个整型数字的运算，如a+6、a-6、axb和a/b等，他才不关心整数在计算机内部是如何表示的，也不想知道CPU为了实现1+2进行几次开关操作，这些操作是如何实现的，对高级语言开发者来讲根本不重要。于是我们就会考虑，无论什么计算机、什么计算机语言，大都会面临着如整数运算、实数运算、宇符运算等操作，我们可以考虑把它们都抽象出来。

抽象是指抽取出事物具有的普遍性的本质。它是抽出问题的特征而忽略非本质的细节，是对具体事物的一个概括。抽象是一种思考问题的方式，它隐藏了繁杂的细节，只保留实现目标所必需的信息。

4.2抽象数据类型

我们对已有的数据类型进行抽象，就有了抽象数据类型。
抽象数据类型 ( Abstract Data Type, ADT)：一个数学模型及定义在该模型上的一组操作。抽象数据类型的定义仅取決于它的一组逻辑特性，而与其在计算机内部如何表示和实现无关。

比如刚才的例子，各个计算机，不管是大型机、小型机、PC、平板电脑、PDA，甚至智能手机都拥有“整数” 类型，也需要整数间的运算，那么整型其实就是一个抽象数据类型，尽管它在上面提到的这些在不同计算机中实现方法上可能不一样，但由于其定义的数学特性相同，在计算机编程者看来，它们都是相同的。因此，“抽象”的意义在于数据类型的数学抽象特性。

而且，抽象数据类型不仅仅指那些已经定义并实现的数据类型，还可以是计算机编程者在设计软件程序时自己定义的数据类型，比如我们编写关于计算机绘图或者地图类的软件系统，经常都会用到坐标。也就是说，总是有成对出现的x和y，在3D系统中还有z出现，既然这三个整型数字是始终在一起出现，我们就定义一个叫point的抽象数据类型，它有x、y、z三个整型变量，这样我们很方便地操作—个point数据变量就能知道这一点的坐标了。

根据抽象数据类型的定义，它还包括定义在该模型上的一组操作。

实际上，抽象数据类型体现了程序设计中问题分解、抽象和信息隐藏的特性。抽象数据类型把实际生活中的问题分解为多个规模小且容易处理的问题，然后建立一个计算机能处理的数据模型，并把每个功能模块的实现细节作为一个独立的单元，从而使具体实现过程隐藏起来。