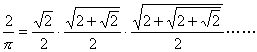精讲C语言之循环结构
精讲C语言之循环结构
常见题型：
1. 穷举
穷举法简单粗暴，没有什么问题是搞不定的，只要你肯花时间。同时对于小数据量，穷举法就是最优秀的算法，但是对于数据量较大的情况下计算机就不容易跑出结果。
难度指数: ⭐⭐
经典题目:
百钱买百鸡
水仙花数 （也可以打表…）
韩信点兵
原创题目:
特殊的年份
题目概况：
输出从公元2世纪~公元101世纪中截止某个年份以来的所有闰年年份中各年份的年份之和为24的年份及特殊年份的个数。
注意：闰年的判别条件是该年年份能被4整除但不能被100整除、或者能被400整除。年份之和指的是各数位之和，例如:1234的年份之和为1+2+3+4=10
测试样例:
输入样例:
题目无输入
输出样例:
888
…
说明：公元2世纪~ 公元101世纪 指的是公元100~10000年
题后反向思考：
如果已知特殊年份个数为88，能否判断各年份之和为多少，如果能，输出该数；如果不能，请说明具体理由。
2.数列求和或求通项
解题技巧：
根据题目条件推出通项公式，求和的话通过an累加即可
难度指数: ⭐⭐
经典题目:
数列求和 （各种求和问题）
斐波那契数列 及其 衍生题目 (上台阶，兔子繁殖问题…) 也有各种变换题目（上台阶改编）。
特殊a串数列求和
原创题目：
数学王子历险记：
数学王子对圆周率的问题研究时间很长，前段时间看到数学家韦达找到了一个无限序列，可以用来生成π的数值近似值；他想要验证公式的正确性，于是便用该公式计算圆周率，经过大量的实验他发现了该公式每一项的值之间的规律。于是便让你猜一下当项数为n时，对应的圆周率为多少？
注意：结果精确到1e-15，为提高精度建议使用double定义浮点类型变量
测试样例:
输入样例: 第一行输入的值表示为第n项
1
输出样例:
2.828427124746190
说明：输入数n据在1~100之间的正整数，输出数据为精确到小数点后15位的浮点数
题后反向思考：
如果已知精确到15位后圆周率的值，从第几项后开始不再变化（前一项和后一项保留15位小数的值相等），请输出该项的系数。
3. 打印指定图案
解题技巧：
根据题目条件找图形打印的规律，例如空格每行的规律，图案每行的个数变化规律，在写循环部分代码时，注意外层控制行数，内层控制行内输出，外层进行每次循环时注意换行。
必备知识：
每个字符对应的ASCII码值，不需要背，但是大小写字母的ASCII范围和转换需要记住，还有特殊字符的ASCII码值
难度指数: ⭐⭐⭐
经典题目:
打印金字塔（字母，数字…）
打印菱形，三角形…
原创题目：
打印空心矩形：给出指定的长宽分别为a，b及字符s；打印该长宽条件下的用字符s组成的空心矩形。
注意：字符s可以表示为特殊符号，大小写字母，数字等
输入样例: 第一行输入的数据分别为 长a，宽b，字符s
3 4 A
输出样例:
aaa
a a
a a
aaa
提示：大写字母转换为小写字母，对应的ASCII码值+32
数据范围：输入数据m,n均为1~100之间的正整数，字符a的ascii码值范围为[32,126]
题后反向思考：
如果已知如果输入小写字母时，要求打印对应大写字母的图案，如果输入大写字母时，要求打印输出对应小写字母的图案，代码如何更改。
4. 数学类题目
解题技巧：
根据定义的数学概念，通过遍历数字判断是否符合相应的特征
难度指数: ⭐⭐⭐⭐
经典题目:
素数（质数）
最大公约数和最小公倍数 （有对应的关系）
卷积，快速幂，费马小定理，欧几里得定理的各种题目 有兴趣可以了解…
原创题目：
已知两个正整数 m 和 n且m <= n，两数最大公因数和最小公倍数为a与b，输出[a,b]之间的所有的质数之和
注意：质数为指在大于1的自然数中，除了1和它本身以外不再有其他因数的自然数；1不是质数，2是质数
测试样例:
输入样例: 第一行输入的数据分别表示 正整数m和n
4 3
输出样例:
28
说明：4 和 3 的最小公因数为1，最大公倍数为12，1-12内的质数有2，3，5，7，11；2+3+5+7+11=28
题后反向思考：
如果已知质数之和为sum，最大公因数和最小公倍数记为a与b，原正整数记为m与n
（1）能否逆向求出唯一的一对a，b的值，如果能输出两数的值，如果不能请说明理由
（2）如果第一问成立的情况下，是否能逆向推出正整数m和n的值，如果能输出两数的值，如果不能请说明理由
定理证明过程：
假设这两个数一个是x，另一个是y。设x和y的最大公约数是A，最小公倍数是B.
那么x÷A和y÷A一定是互质的.所以一定就有B=(x÷A)×(y÷A)×A, 所以AB=xy。
思想引导：
求区间[m，n]内的奇数个数，结果对1000000007取余；数据范围1 <= m，n <= 1018
测试样例:
输入样例:
3 123456789101112
输出样例:
394118459
由此可以推理证明：
前缀和的应用是可以以较小的时间复杂度得到某一区间的和或统计某一区间满足条件的数
int s[n];
int a[n][n];
for(int i=0;i<n;i++){
a[i][0] = s[i];
for (int j=1;j<n;j++){
a[i][j] = a[i][j-1] + s[j];
}
}
通过求出所有区间段和的数，形成一张图，遍历图中元素，利用插入set集合来判断是否有重复的，由此可以证明。
5. 状态类题目
解题技巧：
理解题目中的状态转换的判断条件，通过设置一个标志变量来标志其状态，再通过对其状态的变化来对其进行对应的操作。
常见的状态变量写法有：
bool flag = false;
int status = 0;
// {0, 1, 2, 3, 4} 集合中间的数取值
bool vis[N],v[N]; //N根据题目的数据范围写最大值；
常见题目：
龟兔赛跑（追及问题）
最大子序列和 // 最大子序列积
…
难度指数: ⭐⭐⭐
原创题目：
如何利益最大化：
已知小a在n天内比特币的每日价格为price元/个，某一天买入的比特币只能在之后的某一天卖出(比如第一天的价格为10，第二天价格为8，第三天的价格为15，第一天买入的比特币可以第二天或第三天卖出)，由于资金有限，只能操作一次，求将利益最大化时的获利钱数。
注意：如果最低价时买入n天内都没有合适的价格卖出，则默认没有卖出，收益为0； n的数据范围为1
测试样例:
输入样例: 第一行输入的数据表示n天 第二行输入的数据表示每日的价格price
10
7 5 2 10 13 1 4 13 8 3
输出样例:
12
**说明：显然第6天买入时在最低价1时买入，第8天价格为13时卖出获利最大，利益最大为12 **
题后思考：
有没有一次循环就可以得到最大化利益的值的方法。
拓展题：
如果小a每天通过电脑显卡挖矿可以一天获得一枚比特币，且因为比特币交易市场的限制小a在n天内只能交易一次，求在n天内小a靠挖矿能获得的最大利益及所剩比特币个数（卖出去，转换为现金才算）。
输入样例: 第一行输入的数据表示n天 第二行输入的数据表示每日的价格price
10
7 5 2 10 13 1 4 13 8 3
输出样例: 第一个数据表示最大利益
104 2
说明：显然第8天以最高价13卖出，所获利益最大值为8×13=104 第八天后剩于两天，所以存有比特币个数为2
6. 计算类题目
解题技巧：
理解题目中所要求的最大值，最小值，平均值…。
常见题目：
统计考试成绩 （必须要会）
求绩点 各种求成绩，均价等题目
原创题目：
小a考试的成绩：
已知小a的n门课的考试成绩分别为score1，score2…scoreN，请你帮他分析一下考试成绩中的最大值，最小值，平均值，以及极差值。
注意：每科成绩score均为小于等于100的正整数，n的数据范围为1
测试样例:
输入样例: 第一行输入的数据表示n门考试分数 第二行输入的数据表示每科的考试成绩score
10
97 85 72 100 73 19 78 93 88 63
输出样例:
最高分为： 100
最低分为： 19
平均分为：76.80
极差值为：81
**说明：平均分保留两位小数 **
题后思考：
如何求所有成绩的方差值为多少。