数据结构例题代码及其讲解-图
01 图的邻接矩阵存储结构定义。
- 顶点表、边(二维数组)、顶点数量和边的数量
typedef struct MGraph {
char Vex[MaxSize];//顶点(vertex)中数据
int Edge[MaxSize][MaxSize];//边
int vexnum, arcnum;//顶点数量和边的数量
}MGraph;
图中涉及到.和->的区别。
弧与边:弧:有向图中连接两个节点的媒介通常叫做“弧”。 边:无向图中连接两个节点的媒介通常叫做“边”。而arc表示弧的意思,希望可以对大家记录这几个单词有所帮助。
02 图的邻接表存储结构定义。
//边表结点
typedef struct ArcNode {
int adjvex;//边指向顶点的存储位置
struct ArcNode* nextarc;//指向下一个边表结点的指针域
}ArcNode;
//顶点结点
typedef struct VNode {
char data;//顶点中数据
ArcNode* firstarc;//指向第一个边表结点的指针域
}VNode;
//图
typedef struct AGraph {
VNode adjlist[MaxSize];//邻接表
int vexnum, arcnum;//顶点数量和边的数量
}AGraph;
用邻接表存储图,需要两部分,顶点和边,这里定义了两种结点,
顶点结点:顶点结点用来存放顶点,包括数据域和指针域,其指针域用来指向这个顶点的第一条边
边表结点:边表结点用来表示边之间的关系,也包括数据域和指针域,指针域指向该顶点结点指向边。
顶点结点的指针域是ArcNode类型,也就是边表结点类型,其指向第一个边表结点。
图中定义的是顶点结点类型的数组(数组中的每个元素是顶点结点类型)。
参数定义说明:定义函数传参时,MGraph G是把邻接矩阵表示的图直接传进去了,而AGraph G是直接把邻接表表示的图传进去,但是这种情况比较少见,且主流的参考资料中,在邻接表存储的图中,使用的是AGraph* G,即传进去一个指针,这个指针指向这个图。用指针的方式,则取结构体中的内容时候,需要用->。
void Func(AGraph* G) {
int a = G->vexnum;//a获取图的顶点数量
int b = G->arcnum;//b获取图的边的数量
printf("%c", G->adjlist[0].data);//打印第一个顶点结点的数据
ArcNode* p;//定义一个ArcNode类型的p指针;
p = G->adjlist[0].firstarc;//p初始时指向图的第一个顶点结点的指针域,也就是边表结点
printf("%c", G->adjlist[p->adjvex].data);//通过p指针指向的边表结点的数据域,打印顶点结点
}
上述代码是图的部分操作代码,这里尤其要注意用**.还是->**来表示结构体中内容。

03 写出从图的邻接表表示转换成邻接矩阵表示的算法。
- 邻接表表示的图有邻接表,顶点数量变量和边数量变量,邻接矩阵表示的图有顶点表、边(二维数组)、顶点数量变量和边的数量变量,要将邻接表转换成邻接矩阵,对于顶点数量和边数量,直接复制过来即可,对于如何填充邻接矩阵的顶点表和边(二维数组),需要遍历;
- 这里按行遍历,将邻接表中的顶点信息和边的信息复制过来,在此之前需要对==邻接矩阵初始化==一下,二维数组初始化可以使用两个for循环;
- 遍历需要遍历指针,是边表结点(ArcNode)类型的遍历指针,按行遍历,遍历四行(也就是顶点结点的个数)。
void Func(MGraph& G1, AGraph* G2) {//MGraph表示邻接矩阵,AGraph表示邻接表
G1.vexnum = G2->vexnum;//给图的顶点数量赋值
G1.arcnum = G2->arcnum;//给图的边数量赋值
//初始化邻接矩阵
for (int i = 0; i < G2->vexnum; i++)
for (int j = 0; j < G2->vexnum; j++)
G1.Edge[i][j] = 0;
ArcNode* p;//定义遍历指针
for (int i = 0; i < G2->vexnum; i++) {
//先复制到邻接矩阵的顶点表中
G1.Vex[i] = G2->adjlist[i].data;//将顶点数据值存储在 Vex 数组中
//然后处理边,也就是填充二维数组
p = G2->adjlist[i].firstarc;//指针 p 指向顶点 i 的第一个边表结点
while (p != NULL) {//遍历顶点 i 的所有边表结点
G1.Edge[i][p->adjvex] = 1;//将邻接矩阵中边对应位置改为 1
p = p->nextarc;//指针 p 继续向后遍历
}
}
}
04 写出从图的邻接矩阵表示转换成邻接表表示的算法。
- 邻接矩阵表示的图有顶点表、边(二维数组)、顶点数量变量和边的数量变量,邻接表表示的图有邻接表,顶点数量变量和边数量变量,要将邻接矩阵转换成邻接表,对于顶点数量和边数量,直接复制过来即可,对于如何填充邻接表,需要遍历邻接矩阵;
- 遍历邻接矩阵,如果值为1,说明有边,需要创建边表结点,插入到邻接表,可以采用头插法插入。
- 代码步骤如下:①给邻接表的顶点数量和边数量变量赋值;②填充邻接表的顶点结点;③遍历邻接矩阵(2个for循环遍历二维数组),存在边创建边表结点头插。
void Func(MGraph G1, AGraph * G2) {//MGraph表示邻接矩阵,AGraph表示邻接表
G2->vexnum = G1.vexnum;//给图的顶点数量赋值
G2->arcnum = G1.arcnum;//给图的边数量赋值
//邻接表的顶点结点的填充
for (int i = 0; i < G1.vexnum; i++) {//遍历存储顶点数据的 Vex 数组
G2->adjlist[i].data = G1.Vex[i];//将各顶点数据赋值给邻接表的顶点结点中
G2->adjlist[i].firstarc = NULL;//初始化顶点结点的指针域
}
ArcNode* p;//定义遍历指针
for (int i = 0; i < G1.vexnum; i++) {//遍历邻接矩阵
for (int j = 0; j < G1.vexnum; j++) {
if (G1.Edge[i][j] != 0) {//若两顶点存在边则需建立边表结点
p = (ArcNode*)malloc(sizeof(ArcNode));//创建边表结点
p->adjvex = j;//为边表结点数据域赋值,注意是j不是i
//将边表结点头插到对应位置
p->nextarc = G2->adjlist[i].firstarc;
G2->adjlist[i].firstarc = p;
}
}
}
}
对于邻接表转邻接矩阵:
①复制边和顶点数量,②初始化邻接矩阵,③填充顶点表和填充邻接矩阵在一个for循环里操作;
对于邻接矩阵转邻接表:
①复制边和顶点数量,②填充邻接表的顶点结点,③两个for循环遍历邻接矩阵找边创建结点头插。
05 请写出以邻接矩阵方式存储图的广度优先遍历算法。
- 广度优先遍历又称BFS(Breath First Search),先遍历最近的一层,没了在转到下一个结点,继续;
- 在邻接矩阵上看,就是先遍历指定结点这一行,有的话就依次打印,遍历完后,在去找下一个结点,这里需要考虑是否已经被遍历打印过,图这一章中经常会定义一个辅助数组visited[],初始化时全部设为0,每次遍历一个结点,将其在visited[]中对应内容置为1,表示已经被遍历过了;
- BFS函数需要传入邻接矩阵G,v表示需要从哪个结点开始进行广度优先遍历,以及遍历数组。
- 有些图是非连通图,需要检查是否有结点没有被遍历过,因此需要代码中第22行开始的部分。
BFS 为什么需要队列?
对于 BFS 算法,正如上面所说的,我们需要一层一层遍历所有的相邻结点。那么相邻结点之间的先后顺序如何确定?因此我们需要一个数据结构来进行存储和操作,需要使得先遍历的结点先被存储,直到当前层都被存储后,按照先后顺序,先被存储的结点也会被先取出来,继续遍历它的相邻结点。因此我们可以发现,这个需求不就是我们的队列吗,First In First Out (FIFO) 。因此对于 BFS 我们需要使用 Queue 这样的一个数据结构,来存储每一层的结点,同时**维护『先进先出 FIFO』**的顺序。
void BFS(MGraph G, int v, int visited[]) {//visited[]已经全部初始化为0了
Queue Q;//定义辅助队列 Q
InitQueue(Q);//初始化队列 Q
printf("%c", G.Vex[v]);//打印该顶点数据
visited[v] = 1;//更新遍历数组
EnQueue(Q, v);//将遍历顶点地址入队
while (!IsEmpty(Q)) {//队列不为空则继续循环
DeQueue(Q, v);//出队并让 v 接收出队顶点地址
for (int j = 0; j < G.vexnum; j++){//遍历邻接矩阵的第 v 行
if (G.Edge[v][j] == 1 && visited[j] == 0) {//寻找有边且未被遍历过的顶点
printf("%c", G.Vex[j]);//打印该顶点的数据
visited[j] = 1;//更新遍历数组
EnQueue(Q, j);//将该顶点地址入队
}
}
}
}
void Func(MGraph G, int v) {
int visited[G.vexnum];//定义遍历数组
for (int i = 0; i < G.vexnum; i++)//初始化遍历数组
visited[i] = 0;
BFS(G, v, visited);//从顶点 v 开始进行广度优先遍历
for (int i = 0; i < G.vexnum; i++)//检查图 G 是否有未被遍历到的顶点
if (visited[i] == 0)//若有未被遍历到的顶点则需再次执行 BFS 算法
BFS(G, i, visited);
}
06 请写出以邻接表方式存储图的广度优先遍历算法。
- 邻接矩阵中打印结点值是在顶点表中打印的,而邻接表中打印结点值需要在顶点结点中;
- 邻接矩阵中是遍历二维数组进行广度优先遍历,邻接表遍历边表结点进行广度优先遍历;
- 邻接表中需要遍历指针p才能遍历,邻接矩阵中直接for循环遍历;
- 遍历时,遍历指针p不为空,说明有结点相连,需要进一步判断结点是否已经被遍历过,如果没有被遍历过,打印,更新遍历数组,入队,被遍历过就不去管它,之后需要继续向后遍历。
- 有些图是非连通图,需要检查是否有结点没有被遍历过,因此需要代码中第25行开始的部分。
- 邻接表方式和邻接矩阵方式存储的图的广度优先遍历,主要区别在于邻接表要用遍历指针去遍历,而邻接矩阵可以for循环遍历。
void BFS(AGraph * G, int v, int visited[]) {
Queue Q;//定义辅助队列 Q
InitQueue(Q);//初始化辅助队列 Q
printf("%c", G->adjlist[v].data);//打印地址为 v 的顶点值
visited[v] = 1;//更新遍历数组
EnQueue(Q, v);//将遍历顶点地址入队
ArcNode* p;//定义遍历指针 p
while (!IsEmpty(Q)) {//队列不为空则需继续循环
DeQueue(Q, v);//出队并让 v 接收出队顶点地址
p = G->adjlist[v].firstarc;//p 指针指向顶点 v 的第一个边表结点
while (p != NULL) {//遍历顶点 v 的所有边表结点
if (visited[p->adjvex] == 0) {//判断遍历边表结点对应顶点是否被遍历过
printf("%c", G->adjlist[p->adjvex].data);//遍历其顶点
visited[p->adjvex] = 1;//更新遍历数组
EnQueue(Q, p->adjvex);//将此遍历顶点地址入队
}
p = p->nextarc;//遍历指针继续向后遍历
}
}
}
void Func(AGraph* G, int v) {
int visited[G->vexnum];//定义遍历数组
for (int i = 0; i < G->vexnum; i++)//初始化遍历数组
visited[i] = 0;
BFS(G, v, visited);//从顶点 v 开始进行广度优先遍历
for (int i = 0; i < G->vexnum; i++)//检查图 G 是否有未被遍历到的顶点
if (visited[i] == 0)//若有未被遍历到的顶点则需再次执行 BFS 算法
BFS(G, i, visited);
}
07 请设计一个算法,找出邻接表方式存储的无向连通图 G 中距离顶点 v 最远的一个顶点。(所谓最远就是到达顶点 v 的路径长度最长)
- 考察广度优先遍历(一层一层的遍历),最后进行遍历的结点就是离最开始遍历的结点最远的结点;
- 连通图,不需要考虑一次广度优先遍历没有遍历完结点的情况;
- 在队列中,最后一个出队的结点就是最远的顶点。
int Func(AGraph * G, int v, int visited[]) {//改写 BFS,最后一个出队顶点即为所求
for (int i = 0; i < G->vexnum; i++)//初始化遍历数组
visited[i] = 0;
Queue Q;//定义辅助队列 Q
InitQueue(Q);//初始化队列 Q
visited[v] = 1;//更新遍历数组
EnQueue(Q, v);//令遍历顶点地址入队
ArcNode* p;//定义遍历指针 p
while (!IsEmpty(Q)) {//队列不为空则继续循环
DeQueue(Q, v);//出队并让 v 接收出队顶点地址
p = G->adjlist[v].firstarc;//遍历指针 p 指向顶点 v 的第一个边表结点
while (p != NULL) {//遍历顶点 v 的所有边表结点
if (visited[p->adjvex] == 0) {//若遍历边表结点对应顶点还未被遍历过
visited[p->adjvex] = 1;//更新遍历数组
EnQueue(Q, p->adjvex);//将该遍历顶点地址入队
}
p = p->nextarc;//指针 p 继续向后遍历
}
}
return v;//返回最后一个出队顶点地址
}
08 请写出利用 BFS 算法求解邻接表存储的无权图中单源最短路径的算法。
- 单源最短路径是说,找一个顶点,其到其他顶点的最短路径,一般来说定义一个距离数组,通过广度优先遍历的一层一层的遍历,更新数组中的元素。由于可能不是连通图,因此初始化时,需要将距离设为最大。
- 例如:求解0号位置,也就是A结点的单源最短路径,通过广度优先遍历将B和C在距离数组中的值变成1,A结点遍历完后,遍历1号位置,也就是遍历B结点开始,剩下只有D结点没有被遍历到,因此D的距离数组中的内容应该是B在距离数组中的元素值加1,这里需要注意。
- 单源最短路径的累加(本题的重点是距离数组的更新融入到广度优先遍历算法中)是通过本次开始遍历的顶点在距离数组中的值+1。
void BFS_MIN_Distance(AGraph * G, int v, int visited[], int d[]) {
for (int i = 0; i < G->vexnum; i++) {//初始化遍历数组和距离数组
visited[i] = 0;
d[i] = INT_MAX;
}
Queue Q;//定义辅助队列 Q
InitQueue(Q);//初始化辅助队列 Q
ArcNode* p;//定义遍历指针
visited[v] = 1;//更新遍历数组
d[v] = 0;//单源顶点地址为 v,该顶点到自己的距离为 0
EnQueue(Q, v);//将该顶点地址入队
while (!IsEmpty(Q)) {//队列不为空则继续遍历
DeQueue(Q, v);//出队并让 v 接收出队顶点地址
p = G->adjlist[v].firstarc;//遍历指针 p 指向顶点 v 的第一个边表结点
while (p != NULL) {//遍历顶点 v 的所有边表结点
if (visited[p->adjvex] == 0) {//若遍历边表结点对应的顶点还未被遍历过
visited[p->adjvex] = 1;//更新遍历数组
d[p->adjvex] = d[v] + 1;//更新距离数组
EnQueue(Q, p->adjvex);//将遍历顶点地址入队
}
p = p->nextarc;//遍历指针继续向后遍历
}
}
}
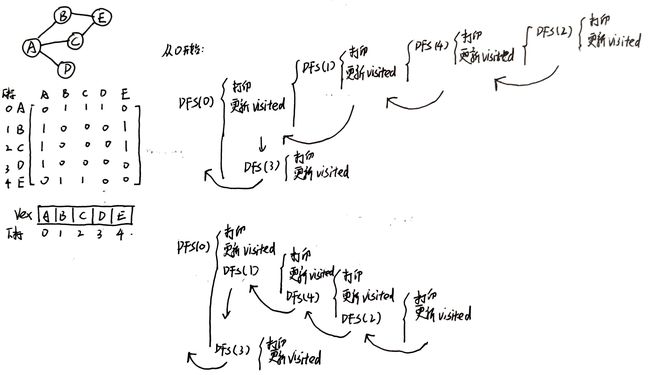
09 请写出以邻接矩阵方式存储图的深度优先遍历算法。
- 深度优先遍历又称DFS(Depth First Search),一直往前走,向前走不了了,往回走,看是否还有其他路可以走。
- 在邻接矩阵中,顶点在其所在行进行查找没有被遍历的顶点,然后跳转到该顶点所在行,依次进行下去;如果找不到没有被遍历的顶点,则返回到上一个顶点所在行,继续往后寻找没有被遍历的顶点。
- 这里涉及到往下递和往回归的过程,可以通过递归编写代码。
- 递归的案例可以看一下
void DFS(MGraph G, int v, int visited[]) {
printf("%c", G.Vex[v]);//打印顶点 v 的数据
visited[v] = 1;//更新遍历数组
for (int j = 0; j < G.vexnum; j++) {//遍历邻接矩阵的第 v 行
if (G.Edge[v][j] == 1 && visited[j] == 0)//寻找第一个有边且未被遍历过的顶点
DFS(G, j, visited);//递归打印顶点 j 的数据值
}
}
void Func(MGraph G, int v) {
int visited[G.vexnum];//定义遍历数组
for (int i = 0; i < G.vexnum; i++)//初始化遍历数组
visited[i] = 0;
DFS(G, v, visited);//从顶点 v 开始进行深度优先遍历
//非连通图的时候需要检查没有被遍历的顶点
for (int i = 0; i < G.vexnum; i++)//检查图 G 是否有未被遍历到的顶点
if (visited[i] == 0)//若有未被遍历到的顶点则需再次执行 DFS 算法
DFS(G, i, visited);
}
10 请写出以邻接表方式存储图的深度优先遍历算法。
- while (p != NULL)和p = p->nextarc;相当于邻接矩阵里面的for循环遍历。
void DFS(AGraph * G, int v, int visited[]) {
printf("%c", G->adjlist[v].data);//打印顶点 v 的数据
visited[v] = 1;//更新遍历数组
ArcNode* p = G->adjlist[v].firstarc;//遍历指针 p 指向顶点 v 的第一个边表结点
while (p != NULL) {//遍历顶点 v 的所有边表结点
if (visited[p->adjvex] == 0)//寻找其未被遍历过的边表结点
DFS(G, p->adjvex, visited);//递归打印该顶点的数据值
p = p->nextarc;//遍历指针继续向后遍历
}
}
void Func(AGraph* G, int v) {
int visited[G->vexnum];//定义遍历数组
for (int i = 0; i < G->vexnum; i++)//初始化遍历数组
visited[i] = 0;
DFS(G, v, visited);//从顶点 v 开始进行深度优先遍历
for (int i = 0; i < G->vexnum; i++)//检查图 G 是否有未被遍历到的顶点
if (visited[i] == 0)//若有未被遍历到的顶点则需再次执行 DFS 算法
DFS(G, i, visited);
}
11 有向图 G 以邻接表方式存储的,请设计一个算法判断图 G 中顶点 i 到顶点 j 是否存在路径。(i 和 j 不相等)
- 考的是图的遍历,假设从顶点i处遍历,经过一次广度优先遍历/深度优先遍历后,去看visited[]数组中顶点j是否被遍历过。
int Path_i_j(AGraph* G, int i, int j) {//此算法省略了 DFS 算法书写
int visited[G->vexnum];//定义遍历数组
for (int k = 0; k < G->vexnum; k++)//初始化遍历数组
visited[k] = 0;
DFS(G, i, visited);//从顶点 i 开始进行深度优先遍历,也可改为 BFS(G,i,visited)
if (visited[j] == 1)//若深度优先遍历执行结束后遍历数组中顶点 j 被遍历了
return 1;//则说明顶点 i 到顶点 j 有路径
else//若顶点 j 未被遍历到,则说明无路径
return 0;
}
12 请设计一个算法判断一个邻接表存储的无向图中有几个连通分量。
- 一开始写的BFS/DFS算法都是争对连通图的算法,如果不是连通图,需要加一个新的函数,判断是否有没有被遍历到的结点,然后重复调用BFS/DFS算法;
- 这里记录连通分量数量也就是改写之前我们写的,也就是看要执行几次遍历,定义一个count变量累加即可。
int Func(AGraph* G) {//此算法省略了 DFS 算法的书写
int visited[G->vexnum];//定义遍历数组
for (int i = 0; i < G->vexnum; i++)//初始化遍历数组
visited[i] = 0;
int count = 0;//定义变量 count 负责记录连通分量的个数
for (int i = 0; i < G->vexnum; i++)//遍历辅助数组
if (visited[i] == 0) {//若存在未被遍历的顶点则以此顶点开始执行 DFS 算法
DFS(G, i, visited);//也可改为 BFS(G,i,visited)
count++;//每执行一次 DFS 算法连通分量个数就加一
}
return count;//最后返回 count 值即为连通分量个数
}
13 试设计一个算法,判断一个邻接表存储的无向图 G 是否为一棵树。
- 算法思想:树的要求:①连通图;②边的数量=顶点数量-1。
- BFS/DFS遍历都可以;
- 一次遍历后,visited[]数组若全为1,说明是连通图,G->arcnum == G->vexnum - 1
- 无向图中,边会计算两次从A->B和从B->A,但是这里默认边的数量是实际边的数量,没有乘以2的情况。
int IsTree(AGraph * G) {//此算法省略了 DFS 算法的书写
int visited[G->vexnum];//定义遍历数组
for (int i = 0; i < G->vexnum; i++)//初始化遍历数组
visited[i] = 0;
DFS(G, 0, visited);//遍历图 G,也可改为 BFS(G,0,visited)
for (int i = 0; i < G->vexnum; i++)//检查图 G 是否有未被遍历到的顶点
if (visited[i] == 0)//若有未遍历顶点,则图 G 不连通,不是树,返回 0
return 0;
if (G->arcnum == G->vexnum - 1)//若图 G 是连通图且满足边数等于顶点数减一
return 1;//则图 G 是树,返回 1
else//若图 G 是连通图但不满足边数等于顶点数减一,则不是树,返回 0
return 0;
}
14 有一个邻接矩阵形式存储的连通图 G,试写出图 G 深度优先遍历的非递归算法。
- 写非递归算法,需要自己定义栈,因为递归也是调用了递归工作栈;
- j == G.vexnum表示没有从上面的for循环中break,也就是说没有边或者有边但是已经被遍历过了,说明这一行没有满足条件的,因此出栈,方便后续回到上一层。
void DFS(MGraph G, int v, int visited[]) {
for (int i = 0; i < G.vexnum; i++)//初始化遍历数组
visited[i] = 0;
Stack S;//定义辅助栈 S
InitStack(S);//初始化栈 S
printf("%c", G.Vex[v]);//打印顶点 v 的数据
visited[v] = 1;//更新遍历数组
Push(S, v);//将该顶点地址压入栈中
int j;
while (!IsEmpty(S)) {//栈不为空则需继续循环
GetTop(S, v);//让变量 v 接收栈顶顶点地址但不出栈
for (j = 0; j < G.vexnum; j++) {//遍历邻接矩阵的第 v 行
if (G.Edge[v][j] == 1 && visited[j] == 0)//寻找有边且还未被遍历的顶点
break;//找到第 v 行满足条件的顶点后,则直接跳出循环
}
if (j == G.vexnum)//若第 v 行没有满足条件的顶点,则出栈
Pop(S, v);
else {//若找到了第 v 行满足条件的顶点
printf("%c", G.Vex[j]);//打印其数据值
visited[j] = 1;//更新遍历数组
Push(S, j);//将该顶点地址压入栈中
}
}
}
15 有一个邻接表形式存储的连通图 G,试写出图 G 深度优先遍历的非递归算法。
- 连通图,只需要写一个函数就行;
- 首先要初始化visited数组,还要自己定义且初始化栈,然后就是打印v顶点的数据且将visited数组更新,然后入栈,由于是邻接表,因此需要遍历指针而且是边表结点的遍历指针,因此这里是ArcNode* p;
- 深度优先遍历由于需要回到上一层,因此一般是不出栈的,而是用变量去接收栈顶元素进行判断,而在邻接表中表示的都是边,因此这里着重判断是否被遍历过p==NULL说明邻接表中一排已经遍历完了,和邻接矩阵的非递归表示【if (j == G.vexnum),Pop(S, v);】即一行遍历完没有符合条件的,需要出栈,方便后续回到上一层。
- p!=NULL,说明找到可以往下遍历的边表结点,打印,更新遍历数组,压栈下一次while循环,读栈顶,p就会从这一行的第一个边表节点开始遍历。
void DFS(AGraph * G, int v, int visited[]) {
for (int i = 0; i < G->vexnum; i++)//初始化遍历数组
visited[i] = 0;
Stack S;//定义辅助栈 S
InitStack(S);//初始化栈 S
printf("%c", G->adjlist[v].data);//打印顶点 v 的数据
visited[v] = 1;//更新遍历数组
Push(S, v);//将该顶点地址值压入栈中
ArcNode* p;//定义遍历指针 p
while (!IsEmpty(S)) {//栈不为空则需继续循环
GetTop(S, v);//让变量 v 接收栈顶顶点地址但不出栈
p = G->adjlist[v].firstarc;//遍历指针 p 指向顶点 v 的第一个边表结点
while (p != NULL && visited[p->adjvex] == 1)//寻找边表结点中未遍历的顶点
p = p->nextarc;
if (p == NULL)//若 p 为空顶点 v 的所有的边表结点都已处理完毕
Pop(S, v);//顶点 v 地址出栈
else {//若指针 p 所指边表结点对应顶点还未遍历过
printf("%c", G->adjlist[p->adjvex].data);//打印其数据值
visited[p->adjvex] = 1;//更新遍历数组
Push(S, p->adjvex);//将该顶点地址压入栈中
}
}
}
邻接矩阵和邻接表的DFS非递归算法的第二个while循环中都需要判断是否整行都不符合往下遍历的条件。
16 假设图用邻接表表示,设计一个算法,输出从顶点 u 到顶点 v 的所有简单路径。
- 简单路径:没有重复结点也找到最终路径,比如A-B-E从顶点A到顶点B,简单路径A-B,非简单路径A-B-E-B;
- 改写**深度优先遍历+回溯**,如果找到了一条简单路径,下一步就要回退一步,试着往其他节点处走,是否能到终点;
- 如果一条路走带头,无路可走,往回退一步;
- path[]代表路径数组,d表示路径数组的下标;
- 首先要将路径数组填充一下,更新遍历数组,如果找到一条路径(寻找顶点即为目标顶点),就打印路径,然后我们需要回溯,去到上一个结点,
void PrintPath(AGraph * G, int u, int v, int visited[], char path[], int d) {//d初始时为-1
d++;//变量 d 为路径数组索引
path[d] = G->adjlist[u].data;//从 u 开始寻找路径
visited[u] = 1;//更新遍历数组
if (u == v) {//若此时开始寻找顶点即为目标顶点则打印路径
for (int i = 0; i <= d; i++)//打印路径数组中存储的路径
printf("%c", path[i]);
visited[u] = 0;//回溯
return;
}
ArcNode* p = G->adjlist[u].firstarc;//深度优先遍历改写
while (p != NULL) {
if (visited[p->adjvex] == 0)
PrintPath(G, p->adjvex, v, visited, path, d);//当前顶点开始继续寻找路径
//上面的if判断如果成立,从顶点结点指向的边表结点开始继续递归,直到最上面的
p = p->nextarc;
}
visited[u] = 0;//更新遍历数组,回溯寻找是否有其它路径
}
//主函数
void Func(AGraph* G, int u, int v) {
int visited[G->vexnum];//定义遍历数组
char path[G->vexnum];//定义路径数组,这里可以不初始化,因为后面是先更新path数组,然后打印。
for (int i = 0; i < G->vexnum; i++)//初始化遍历数组
visited[i] = 0;
PrintPath(G, u, v, visited, path, -1);//调用函数输出两顶点的所有简单路径
}
大家可以参考下回溯法的模板
//一定要分成横纵两个方面思考回溯
void backtracking(参数) {
if (终止条件) {
存放结果;
return;
}
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {//注意i=0,i=start的区别
处理节点;
backtracking(路径,选择列表); // 递归 注意(i)和(i++)的区别 后面会懂
回溯,撤销处理结果
}
}
for/while循环横向遍历,递归纵向遍历,回溯不断调整结果集
17 请写出邻接表存储有向图的拓扑排序算法。
- 拓扑排序(不唯一):对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序,是将G中所有顶点排成一个线性序列,使得图中任意一对顶点u和v,若边(u,v)∈E(G),则u在线性序列中出现在v之前。
- 拓扑排序的步骤:①按照一定的顺序进行构造有向图,记录后个节点的入度;②从图中选择一个入度为0的顶点,输出该顶点; ③从图中删除该顶点及所有与该顶点相连的边;④重复上述两步,直至所有顶点输出。 ⑤或者当前图中不存在入度为0的顶点为止。此时可说明图中有环。
- 由于需要考虑到入度,可以在顶点结点处结构体定义一下,加一个入度的变量;
- 有环的情况,可以定义一个count计数变量
- 初始化好栈后,第一步找是否有入度为0的结点,有则将其入栈(栈中存放的是入度为0的结点),如果栈不为空,说明有入度为0的结点,出栈(用i去接收),打印,这里处理了,count++,然后就需要将出栈的顶点指向的所有顶点的入度减一,减到0了就要将其压栈;
- 最后只需要比较count和顶点数量是否相等,不相等说明有环。
结构体定义
//边表结点
typedef struct ArcNode {
int adjvex;
struct ArcNode* nextarc;
}ArcNode;
//顶点结点
typedef struct VNode {
char data;
int indegree;//顶点结点结构体增加了一个记录入度的成员
ArcNode* firstarc;
}VNode;
typedef struct AGraph {
VNode adjlist[MaxSize];
int vexnum, arcnum;
}AGraph;
int Top(AGraph* G) {
int i = 0, count = 0;//i在入栈出栈时使用,定义变量 count 记录拓扑排序顶点的个数
ArcNode* p;//定义遍历指针 p
Stack S;//定义栈 S
InitStack(S);//初始化栈 S
for (; i < G->vexnum; i++)//遍历邻接表的顶点结点
if (G->adjlist[i].indegree == 0)//将入度为 0 的顶点压入栈中
Push(S, i);
while (!IsEmpty(S)) {//栈不为空则证明还有入度为 0 的顶点需要处理
Pop(S, i);//出栈,让变量 i 接收出栈顶点地址
printf("%c", G->adjlist[i].data);//打印出栈顶点数据值
count++;//记录打印过的顶点个数
//⭐将出栈的顶点指向的所有顶点的入度减一
p = G->adjlist[i].firstarc;//遍历指针 p 指向出栈顶点的第一个边表结点
while (p != NULL) {//遍历出栈顶点的所有边表结点
G->adjlist[p->adjvex].indegree--;//该顶点指向的顶点入度减一
if (G->adjlist[p->adjvex].indegree == 0)//判断入度减一后是否等于 0
Push(S, p->adjvex);//若等于 0 则压入栈中,等待处理
p = p->nextarc;//遍历指针继续遍历
}
}
if (count == G->vexnum)//若循环结束所有顶点都已打印,则拓扑排序成功
return 1;
else//若循环结束打印顶点数小于顶点个数,则该图有环,拓扑排序失败
return 0;
}
18 请设计一个算法判断一个邻接表存储的无向图中是否有环。
- 方法不唯一,其中一个简单易懂的方法:和之前判断无向图是否构成一棵树的思想类似①是否为连通图②边=顶点-1(也是图的一个临界条件),若边再少一条,就不是连通图了,如果再加一条边,就构成了环。如果不是连通图,边=顶点数-连通分量数,如果边>顶点数-连通分量数,说明有环,这里不存在边<顶点数-连通分量数,因为一旦边少了一条,连通分量+1,左右都减去1,又平衡了。
- Func()返回的是连通分量个数
int Func(AGraph * G) {//函数功能:计算图 G 中连通分量个数
int visited[G->vexnum];//定义遍历数组
for (int i = 0; i < G->vexnum; i++)//初始化遍历数组
visited[i] = 0;
int count = 0;//定义变量 count 负责记录连通分量的个数
for (int i = 0; i < G->vexnum; i++)//遍历辅助数组
if (visited[i] == 0) {//若存在未被遍历的顶点则以此顶点开始执行 DFS 算法
DFS(G, i, visited);//此算法省略了 DFS 算法的书写
count++;//每执行一次 DFS 算法连通分量个数就加一
}
return count;//最后返回 count 值即为连通分量个数
}
int IsLoop(AGraph* G) {
int n = Func(G);//定义变量 n 记录图中连通分量个数
if (G->arcnum == G->vexnum - n)//若满足临界条件,则该无向图不存在环
return 0;
else//若边的数量大于临界条件,则该无向图存在环
return 1;
}
如何判断有向图中是否有环呢--拓扑排序,拓扑排序失败,说明有环。
19 请写出构造最小生成树的 Prim 算法。
- 生成树,包含连通图中所有的顶点,且任意两顶点之间有且仅有一条通路(边=顶-1)
- 最小生成树,找出来的所有边,权值之和最小,最小生成树不是唯一的,但是最小生成树的权值之和是唯一的。
- 使用邻接矩阵构造图,因为邻接矩阵中存放权值比较方便;
- 首先要告诉程序从哪个顶点开始找边,lowcost[]数组用来存储当前最小生成树到其他各顶点的最短距离,每次最小生成树更新,lowcost[]也要更新。对于visited[]数组,先通过for循环进行初始化,对于lowcost[]数组,初始化时候,就是对应v顶点所在邻接矩阵的那一行(此时,这行就是该顶点到其他顶点的最短距离),然后更新visited[]数组,将顶点v所在的元素变成1,说明已经加入最小生成树了。然后就是重点了,就是需要找最小生成树的顶点到其他顶点最短距离的顶点,也就是找那条链接最小生成树的最短的边,因此这个循环查找的次数就是**顶点-1**次,每次查找将变量min设置为整型变量的最大值,方便后续更新其值,由于lowcost[]数组中存放的就是当前最小生成树到其他顶点的最短距离,我们遍历它,找到里面的最小值和顶点元素,如果遍历过程中找到之前没有被遍历过的顶点(没有加到最小生成树中的顶点)且其在lowcost[]数组中的距离比min还要小,因此需要更新min和顶点k的值,遍历完成后,则找到了最短距离及顶点,visited[]数组中其对应的元素置为1,最后需要更新lowcost[]数组,因为最小生成树加入了一个顶点,lowcost[]可能会发生变化。每次加入顶点后,用邻接矩阵中新加入顶点所在行与原来lowcost[]数组进行比较,如果变小了,需要更新lowcost[]数组。
void Prim(MGraph G, int v) {
int visited[G.vexnum];//记录当前最小生成树中包含的顶点
int lowcost[G.vexnum];//记录当前最小生成树到其它各顶点的最短距离
for (int i = 0; i < G.vexnum; i++) {//初始化辅助数组
visited[i] = 0;
lowcost[i] = G.Edge[v][i];
}
printf("%d", G.Vex[v]);//打印当前加入最小生成树的顶点
visited[v] = 1;//更新辅助数组
int min, k;//定义变量 min 记录当前最小生成树到其它顶点的最小距离
for (int i = 0; i < G.vexnum - 1; i++) {//共需找顶点个数减一条边
min = INT_MAX;//每一次寻找前都需要初始化 min
for (int j = 0; j < G.vexnum; j++)//遍历记录距离的数组
if (visited[j] == 0 && lowcost[j] < min) {//寻找此时距离最小的边
min = lowcost[j];//min 记录最小生成树到其它顶点的最小距离
k = j;//k 记录最小权值边对应的顶点
}
printf("%d", G.Vex[k]);//打印当前加入最小生成树的顶点
visited[k] = 1;//更新辅助数组
for (int j = 0; j < G.vexnum; j++)//更新记录最小生成树到其它顶点距离的数组
if (visited[j] == 0 && G.Edge[k][j] < lowcost[j])
lowcost[j] = G.Edge[k][j];
}
}
20 请写出构造最小生成树的 Kruskal 算法。
- 边按照权值递增的次序进行找,看是否合适(成环就不合适了);
- ①构造新的结构体存储边相关的信息,包括起始顶点,结束顶点,权值;②然后进行递增排序;③使用并查集进行
typedef struct {//存储边的结构体
int s;//记录边的起点start
int e;//记录边的终点end
int weight;//记录边的权值
}edge;
int Find(int S[], int x) {//在并查集 S 中查找 x 所在集合的根
while (S[x] >= 0)
x = S[x];
return x;
}
- 邻接矩阵是对称的,只需要遍历上三角或者下三角就行。首先将邻接矩阵中的各边权值放到存放边信息的结构体中,然后对其排序
void Kruskal(MGraph G) {
edge e[G.arcnum];//定义保存图中所有边的辅助数组
int k = 0;//记录数组下标
for (int i = 0; i < G.vexnum; i++)//①遍历邻接矩阵,将所有的边存储到辅助数组中
for (int j = i + 1; j < G.vexnum; j++) {
e[k].s = i;//边的起点
e[k].e = j;//边的终点
e[k].weight = G.Edge[i][j];//边的权值
k++;//继续处理下一个数组元素
}
//②递增排序
edge temp;//定义辅助变量 temp 保存待排序元素
for (int i = 1; i < G.arcnum; i++)//直接插入排序
if (e[i].weight < e[i - 1].weight) {
temp = e[i];
for (int j = i - 1; temp.weight < e[j].weight; j--)
e[j + 1] = e[j];
e[j + 1] = temp;
}
//③并查集操作
int S[G.vexnum];//定义数组存储并查集
int count = 0;//定义变量 count 记录符合要求边的数量
int start, end;//定义两变量分别保存边起点和终点所在集合的根
for (int i = 0; i < G.vexnum; i++)//初始化并查集数组
S[i] = -1;
for (int i = 0; i < G.arcnum; i++) {//遍历保存边的辅助数组
start = Find(S, e[i].s);//查找边的起点所在集合的根
end = Find(S, e[i].e);//查找边的终点所在集合的根
if (start != end) {//若边的起点和终点在不同集合,则此条边符合要求
S[start] = end;//将边的起点和终点合并为一个集合里
printf("%d - %d", e[i].s, e[i].e);//打印此边
count++;//更新计数变量
if (count == G.vexnum - 1)//保留边的数量等于顶点数减一则任务完成
break;
}
}
}
21 请写出求单源最短路径的 Dijkstra 算法。
- 之前求过单源最短路径,是对于无权图来说的,可以修改广度优先遍历实现,这次是对于有权图来说的。
- visited[]先初始化为0,dist[]和path[]也要初始化,dist[]中先把顶点v在邻接矩阵中的那权值复制过来,并且将path[]中初始化为v;
void Dijkstra(MGraph G, int v) {
int visited[G.vexnum];//记录各顶点是否找到最短路径,找到置为1,没找到置为0
int dist[G.vexnum];//记录目前源点到各顶点的最短距离
int path[G.vexnum];//记录目前源点到各顶点最短路径的前驱顶点
for (int i = 0; i < G.vexnum; i++)//初始化辅助数组
visited[i] = 0;
for (int i = 0; i < G.vexnum; i++) {//初始化辅助数组
dist[i] = G.Edge[v][i];
path[i] = v;
}
visited[v] = 1;//已确定源点 v 的最短路径
int min, k;//定义变量 min 记录目前未确定最短路径顶点中的最小距离,k对应最短路径的顶点
//已经确定了一个顶点,只需要在确定顶点数-1个顶点就好。
for (int i = 0; i < G.vexnum - 1; i++) {//每次循环确定一个顶点的最短路径
min = INT_MAX;//初始化记录最小值的变量 min
for (int j = 0; j < G.vexnum; j++) {//遍历记录距离的数组
if (visited[j] == 0 && dist[j] < min) {
min = dist[j];//变量 min 记录未确定最短路径顶点中的最小距离
k = j;//变量 k 记录最小距离对应的顶点
}
}
visited[k] = 1;//已确定顶点 k 的最短路径
for (int j = 0; j < G.vexnum; j++) {//更新距离数组
if (visited[j] == 0 && dist[k] + G.Edge[k][j] < dist[j]) {
dist[j] = dist[k] + G.Edge[k][j];//发现更短路径则更新距离数组
path[j] = k;//更新路径数组
}
}
}
}
22 请写出求各顶点之间最短路径的 Floyd 算法。
- 用到了动态规划的算法思想:
void Floyd(MGraph G) {
int i, j, k;
int A[MaxSize][MaxSize];//定义二维数组记录两顶点间最短距离
int path[MaxSize][MaxSize];//定义二维数组记录最短路径中转点
for (i = 0; i < G.vexnum; i++) {//初始化两个二维数组
for (j = 0; j < G.vexnum; j++) {
A[i][j] = G.Edge[i][j];//根据顶点间的直连边计算初始顶点间最短距离
path[i][j] = -1;//初始时顶点间最短路径没有中转点
}
}
for (k = 0; k < G.vexnum; k++) {//变量 k 为此次循环的中转点
for (i = 0; i < G.vexnum; i++) {//遍历两个二维数组
for (j = 0; j < G.vexnum; j++) {
if (A[i][k] + A[k][j] < A[i][j]) {//中转点加入是否需要更新最短距离
A[i][j] = A[i][k] + A[k][j];//更新顶点 i 到 j 的最短距离
path[i][j] = k;//更新顶点 i 到 j 的最短路径中转点
}
}
}
}
}
void PrintPath(int u, int v, int A[][MaxSize], int path[][MaxSize]) {//打印最短路径
if (A[u][v] == INT_MAX)//顶点 u 到 v 没有路径
printf("顶点%d到顶点%d没有路径", u, v);
else if (path[u][v] == -1)//顶点 u 到 v 有直达路径
printf(" %d - %d", u, v);
else {//顶点 u 到 v 有中转路径
int mid = path[u][v];//定义变量 mid 记录顶点 u 到 v 的最短路径中转点
PrintPath(u, mid, A, path);//递归打印顶点 u 到中转点 mid 的最短路径
PrintPath(mid, v, A, path);//递归打印中转点 mid 到顶点 v 的最短路径
}
}