leetcode刷题笔记-链表的使用

一、单链表的基础：增删改查

• 问题：设计一个单链表，要求实现其增删改查功能。707. 设计链表

• 问题分析

  • 往链表中添加元素的步骤
    

  • 往链表中删除元素的步骤

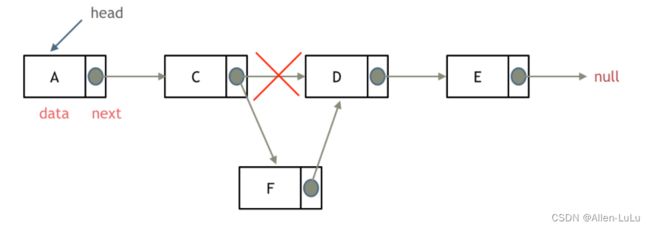
• 注意：对于单链表来说，添加一个无用的头节点，再对链表进行增删操作，可以忽略头尾的特殊情况，使代码统一

• 解决方案

  type listNode struct{
      val int
      next *listNode
  }
  
  func newListNode(val int)*listNode{
      return &listNode{
          val:val,
          next:nil,
      }
  }
  
  type list struct{
      head *listNode
      length int
  }
  
  func newList()*list{
      return &list{
          head:newListNode(-1),
          length:0,
      }
  }
  
  /*--------------------------插入-----------------------------------*/ 
  
  // 头插
  func (l *list)addAtHead(val int){
      newNode := newListNode(val)
      newNode.next = l.head.next
      l.head.next = newNode
      l.length++
  }
  
  // 尾插
  func (l *list)addAtTail(val int){
      cur := l.head
      for cur.next != nil{
          cur = cur.next
      }
      newNode := newListNode(val)
      cur.next = newNode
      l.length++
  }
  
  // 任意位置插入
  func (l *list)addAtIndex(val,index int){
      if index < 0 || index > l.length{
          return
      }
      pre,cur :=l.head ,l.head.next
      for i:=0;i<index;i++{
          pre = cur
          cur = cur.next
      }
      newNode := newListNode(val)
      newNode.next = cur
      pre.next = newNode
      l.length++
  } 
  
  // 打印链表
  func (l *list)printList(){
      cur := l.head.next
      for cur != nil{
          fmt.Printf("%v ",cur.val)
          cur = cur.next
      }
      fmt.Printf("\n")
  }
  
  /*--------------------------删除-----------------------------------*/
  // 任意位置删除
  func (l *list)deleteListNodeByIndex(index int){
      if index < 0 || index > l.length-1{
          return
      }
      pre,cur := l.head,l.head.next
      for i:=0;i<index;i++{
          pre = cur
          cur = cur.next
      }
      pre.next = cur.next
      cur.next = nil
      l.length--
  }
  
  // 按照指定元素删除
  func (l *list)deleteListNodeByVal(val int){
      pre,cur := l.head,l.head.next
      for cur != nil{
          if cur.val == val{
              pre.next = cur.next
              cur.next = nil
              l.length--
          }
          pre = cur
          cur = cur.next
      }
  }
  
  /*--------------------------查找-----------------------------------*/
  // 根据索引查找
  func (l *list)getByIndex(index int)int{
      if index < 0 || index > l.length-1{
          return -1
      }
      cur := l.head.next
      for i:=0;i<index;i++{
          cur = cur.next
      }
      return cur.val
  }
  

二、进阶一：翻转链表

2.1 问题1：翻转链表

• 问题:206. 反转链表

• 解题思路

  • 分析一下，要翻转链表，需要两个指针，一个指向已经翻转好的链表头，一个指向下一个待翻转的节点
  • 首先当前节点指向前面的节点，完成当前节点的翻转
  • 将pre指针移向已经翻转完的节点
  • 将cur指针移动向下一个未翻转的节点

• 解决方案

  // 注意：这里反转链表带着一个无用头节点
  func (l *list)reverseList() {
      var pre *listNode
      cur := l.head.next
      for cur != nil{
          next := cur.next
          cur.next = pre
          pre = cur
          cur = next
      }
      l.head.next = pre  // 实际上，翻转链表用不上头节点，只是由于前面定义的链表都带上了头节点，为了统一代码，这里多余了一步操作头节点
  } 
  

2.2 问题2：两两交换链表节点(难题)

• 问题:给你一个链表，两两交换其中相邻的节点，并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题24. 两两交换链表中的节点

• 问题分析

  • 由于题目要求两两交换，所以我们先得使用双指针找到需要交换的两个节点
  • 同时，我们需要一个指示器，我们每次只交换指示器后面的两个节点，当指示器节点不足两个时，则无需交换了
  • 交换步骤如下
    • 首先将指示器后面的两个节点分别命名为node1,node2
    • 在交换前，temp的next本来是指向node1的，但交换后，temp的next应该指向node2，因此先将temp.next指向node2
    • 将node1的next指向node2的next
    • 将node2的next指向node1
    • 上述步骤完成后，node2与node1已经交换位置,此时由于是node1继续指向后面未交换的节点，因此将指示器移向node1

• 解决方案

  func (l *list)swapPairs(){
      temp := l.head // temp作为指示器，当指示器后面满足有两个节点时，将这两个节点交换
      for temp.next != nil && temp.next.next != nil{
          node1 := temp.next
          node2 := temp.next.next
          temp.next = node2
          node1.next = node2.next
          node2.next = node1
          temp = node1
      }
  }
  

• 练习题：

  • 92. 反转链表 II - 力扣（Leetcode）
  • 25. K 个一组翻转链表 - 力扣（Leetcode）

三、进阶二：使用快慢指针

3.1 问题1：删除链表倒数第n个节点

• 问题：删除链表的倒数第n个节点，要求只能遍历链表一次。

• 问题分析

  • 这题最简单的思路，就是先计算链表的长度l，然后再从链表的头开始，遍历到第l-n个位置删除节点即可，可是这样子，就需要遍历链表两遍（计算链表长度时通常需要遍历一遍链表），不符合题意。
  • 本题可以使用快慢指针来解决，在链表中，快慢指针通常用于以下几种情况
    • 寻找某个特定位置的节点，比如倒数第n个，链表中点等等
    • 判断链表成环，如果链表有环，通过该链表的快慢指针一定能在某个位置相遇
  • 本题可以使用快慢指针解题，关键思路是要理清楚快指针的起点（慢指针通常只走一步）
    • 慢指针一步步走，最终目的是走到倒数第n个位置的前一个位置（这样才能删除倒数第n个位置）
    • 那么，快指针的起始位置，就必须要比慢指针大n
    • 之后，快慢指针一起走，当快指针走完链表的时候，慢指针就在对应的位置了

• 解决方案

  func (l *list)removeNthFromEnd(n int){
      s,f := l.head,l.head
      // 设置快指针的起始位置
      for i:= 0;i<=n;i++{
          f = f.next
      }
      
      // 快慢指针同时移动
      for f != nil{
          s = s.next
          f = f.next
      }
      
      // 快指针遍历完链表时，慢指针刚好走到倒数第n个节点的前一个结点
      next := s.next
      s.next = next.next
      next.next = nil
    
  }
  

3.2 问题二：链表相交问题

• 问题:给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表没有交点，返回 null 面试题 02.07. 链表相交

• 问题分析

  • 链表相交，与环链问题相似，可以使用快慢指针。
  • 快慢指针，优先考虑快指针的起点，这道题很容易想到，只要将快指针放到与慢指针差值为两个链表的插值的位置，就可以让快慢指针同步走到交点处重合。

• 解决方案

  func getIntersectionNode(lA, lB *list) *listNode{
      if lA.length > lB.length{
          diff := lA.length - lB.length
          curA := lA.head.next
          curB := lB.head.next
          for i:=0;i<diff;i++{
              curA := curA.next
          }
          for curA != nil || curB != nil{
              if curA == curB{
                  return curB
              }
              curA = curA.next
              curB = curB.next
          }
      }else{
          diff := lB.length - lA.length
          curA := lA.head.next
          curB := lB.head.next
          for i:=0;i<diff;i++{
              curB := curB.next
          }
          for curA != nil || curB != nil{
              if curA == curB{
                  return curA
              }
              curA = curA.next
              curB = curB.next
          }
      }
  }
  

3.3 问题三：环链问题

• 问题:证明一个链表是否成环，如果成环，返回入环点142. 环形链表 II

• 问题分析

  • 证明环链问题，优先想到快慢指针，当快慢指针能够重合，说明链表内有环
  • 这里得知道一个小技巧,当快慢指针重合时，让一个指针从链表的第一个节点（并非无用头节点）开始，与慢指针同步移动，当它们重逢时，那个点即为入环点

• 解决方案

  func (l *list)detectCycle(head *list) *listNode {
    slow, fast := l.head.next, l.head.next
      for fast != nil {
          slow = slow.Next
          if fast.Next == nil {
              return nil
          }
          fast = fast.Next.Next
          if fast == slow {
              p := l.head.next
              for p != slow {
                  p = p.Next
                  slow = slow.Next
              }
              return p
          }
      }
      return nil
  }
  

三、利用链表数据结构实现常用结构与算法

3.1 哈希集合，使用链表解决哈希碰撞

• 问题：705. 设计哈希集合 - 力扣（Leetcode）

• 分析

  • 哈希表首先需要有一个哈希函数，哈希函数负责将key值映射到哈希集合中去

  • 但是，不同的key可能会hash到相同的哈希值，如果此时直接将value写到对应位置，就会覆盖掉另一个key的值，这就是哈希碰撞。解决哈希碰撞的方法有多种

    • 开放地址法：一旦发生冲突，就去找下一个空的位置，只要散列表足够大，空的散列地址总能找到
    • 链地址法：一旦发生冲突，我们可以在冲突位置构建一个链表，将冲突的数据放到链表中，在寻找key时先通过hash函数获得映射地址，然后从映射地址的链表头开始遍历寻找key即可
    • 公共区溢出法：在另外一个地方开一块连续的空间，这块空间称为公共区。将发生冲突的数据放到公共区。在寻找key时，先根据hash值寻找对应的地址，如果发现该位置的key不是要找的key，那么就到公共区去顺序遍历寻找key

  • 这里使用链地址法解决哈希冲突，构建一个哈希集合

• 方案（这里没有完全按照leetcode上的题目来设计，如果直接复制代码是跑不通的）

  // entry 是哈希集合中实际存放的数据结构
  type entry struct{
      key interface{}
      value interface{}
  }
  
  type hashFunc func(key interface{})int
  
  type Hash struct{
      hash hashFunc
      bucket []*list.List // 用于存放数据的空间，这里称之为桶
  }
  
  func NewHash(base int,hash hashFunc)*Hash{
      return &Hash{
          hash:hash,
          bucket:make([]*list.List,base)
      }
  }
  
  func (h *Hash)Add(key,value interface{}){
      if !h.Contain(key){ // 哈希集合是不允许有相同的key的，先判断哈希集合中是否有key
           hashKey := h.hash(key) //  先获取key的映射地址
          if h.bucket[hashKey] == nil{
              h.bucket[hashKey] = list.New()
          }
          entry := &entry{
              key:key,
              value:value,
          }
          h.bucket[hashkey].PushBack(entry)
      }
  }
  
  func (h *Hash)Contain(key interface{})bool{
      hashKey := h.hash(key)
      if h.bucket[hashKey] != nil{
          for e := h.bucket[hashKey].Front();e != nil;e = e.Next(){
              if e.Value.(*entry).key == key{
                  return true
              }
          }
      }
      return false
  }
  
  func (h *Hash)Get(key interface{})interface{}{
      hashKey := h.hash(key)
      if h.bucket[hashKey] == nil || h.bucket[hashKey].Len() == 0{
          return -1
      }
      for e := h.bucket[hashKey].Front();e != nil ;e = e.Next(){
          if e.Value.(*entry).key == key{
              return e.Value.(*entry).value
          }
      }
      return -1
  }
  
  func (h *Hash)Remove(key interface{}){
      if !h.Contain(key){
          return
      }
      hashKey := h.hash(key)
      for e:= h.bucket[hashKey].Front();e != nil;e = e.Next(){
          if e.Value.(*entry).key == key{
              h.bucket[hashKey].Remove(e)
          }
      }
  }
  

3.2 LFU淘汰策略（最少访问频次淘汰策略）

• 问题：460. LFU 缓存 - 力扣（Leetcode）

• 分析

  • LFU为最少访问频次的淘汰策略，因此，对于每一个key，我们都需要维护一个计数器去记录这个key的访问频率
  • 由于cache中的key不能重复，我们必须要用一个map（这里命名为cacheMap）来记录当前cache中有哪些key（如果不用map记录的话，每次插入key的时候都要从头遍历查找key，时间复杂度太高）
  • cacheMap记录的是key与真实数据的映射，那么我们应该用什么结构保存数据呢？官方题解给出的是二叉树结构，这里我们用golang标准库中提供的双向循环链表来保存数据
    • 想象一下，如果我们只用一个链表是否能满足LFU的请求？
      • 由于按照访问频次最少的淘汰策略，因此我们的链表可以设计如下规则：
        • 将当前最少访问频次的节点放到链表头
      • 根据上述规则，我们每次put或者get的时候都要比较整个链表各个节点的访问频次，然后重新排列链表，这个时间开销是很大的。其次，我们无法保证频次相同的时候的优先淘汰的是最近没有访问的
    • 使用一个链表之所以难以实现LFU，是因为我们既要关注访问频次，还要关注访问顺序，因此，我们能否通过某一个结构，将某个条件固定，只关注另外一个条件呢？方法就是再添加一个map（这里命名为list），该map用于记录不同访问频次的数据到其存储链表的映射
      • 通过使用list记录访问次数，我们就可以将同一访问频次的数据放到同一个链表中，每次put或者get的时候，我们只需要把数据放到对应访问频次的链表即可
      • 对于同一访问频次的链表，我们可以将最近访问的数据通过头插法插入链表头部，那么当要淘汰的频次是当前频次时，我们可以从链表尾部开始淘汰即可
      • 淘汰数据时，我们还是需要找到当前cache的最低访问频次的，难道我们每次都要重新遍历整个map去找最低的访问频次吗？其实我们可以在cache中维护一个字段minCnt，专门记录当前cache中的最低访问频次，这样，在淘汰时，我们就可以直接通过map定位到对应频次的链表了
  • minCnt记录的是当前cache中最小的访问频次，那么我们应该如何维护呢？
    • GET操作：
      • 首先，我们要通过cacheMap[key]定位到对应的数据节点，然后获取数据当前的访问次数cnt
      • 然后，我们将该节点从对应的链表处移除（因为GET一定会修改数据的访问频次，因此数据不可能还呆在原来频次的链表中）
      • 如果此时cnt与minCnt相等，且cnt频次的链表空了，说明此时这个key就是当前cache中访问频次最少的key了，此时，由于get操作，key的访问频次需要+1，而minCnt也需要+1
      • 然后将修改了访问频次后的数据节点加入到新频次对应的链表即可
    • PUT操作：
      • 若key为cache已存在的节点，那么操作和GET操作是近似的，只是多了一步，将旧的value改为新的value即可
      • 若key为新的，那么就要将minCnt重置为1，因为一个新的节点加入，那么当前cache的最低访问频次肯定为1！然后将新的节点插入到频次为1的链表即可

• 设计方案

  // entry为链表中实际存放的数据，之所以要存放key，是为了淘汰节点后能到cacheMap中去删除对应的映射
  type entry struct{
      key interface {}
      value interface {}
      cnt int // 记录当前节点的访问次数
  }
  
  type LFUCache struct{
      capacity int // 最大容量
      size int // 当前cache的容量
      minCnt int // 当前cache中访问最低的频次，用于配合list定位需要淘汰的节点
      cache map[interface{}]*list.Element // 用于记录key与真实节点的地址映射
      list map[int]*list.List // 用于存放不同频次的数据
  }
  
  func NewLFUCache(cap int)*LFUCache{
      return &LFUCache{
          capacity:cap,
          size:0,
          minCnt:0,
          cache:make(map[interface{}]*list.Element),
          list:make(map[int]*list.List),
      }
  }
  
  func (this *LFUCache)Get(key interface{})interface{}{
      if this.size == 0{
          return -1
      }
      if ele,ok := this.cache[key];ok{
          Value := this.list[ele.Value.(*entry).cnt].Remove(ele) // 从当前频次链表中删除节点
          if this.minCnt == Value.(*entry).cnt && this.list[Value.(*entry).cnt].Len() == 0{
              this.minCnt++
          }
          Value.(*entry).cnt++
          if _,ok := this.list[Value.(*entry).cnt];!ok{
              this.list[Value.(*entry).cnt] = list.New()
          }
          e := this.list[Value.(*entry).cnt].PushFront(Value) // 将节点插入到新频次的链表中，返回新的节点地址
     		this.cache[key] = e        
      }
      return -1
  }
     
  func (this *LFUCache) Put(key,value interface{}){
      if this.capacity == 0{
          return
      }
      if ele,ok := this.cache[key];ok{ //key本来就在cache中，操作与GET相似，多了一步修改value的值
           Value := this.list[ele.Value.(*entry).cnt].Remove(ele) // 从当前频次链表中删除节点
          if this.minCnt == Value.(*entry).cnt && this.list[Value.(*entry).cnt].Len() == 0{
              this.minCnt++
          }
          Value.(*entry).cnt++
          Value.(*entry).value = value // 将节点中的value修改为新的value
          if _,ok := this.list[Value.(*entry).cnt];!ok{
              this.list[Value.(*entry).cnt] = list.New()
          }
          e := this.list[Value.(*entry).cnt].PushFront(Value) // 将节点插入到新频次的链表中，返回新的节点地址
     		this.cache[key] = e  //将新的节点地址记录到cache中      
      }else{ // 插入新的数据节点
          // 在插入新节点前，先判断当前cache容量是否满了，如果满了就要淘汰
          if this.size == this.capacity{
              ele := this.list[this.minCnt].Back() // 从访问频次最低的链表尾端淘汰，一定是访问频次最低且最近未访问的数据
              Value := this.list[this.minCnt].Remove(ele)
              this.cache = delete(this.cache,Value.(*entry).key) // 根据key删除掉淘汰的节点映射
              this.size--
          }
          this.minCnt = 1 //由于有新的节点插入，当前cache最低访问频次必为1
          entry := &entry{
              key:key,
              value:value,
              cnt:1,
          }
          if _,ok := this.list[this.minCnt];!ok{
              this.list[this.minCnt] = list.New()
          }
          e := this.list[this.minCnt].PushFront(entry)
          this.cache[key] = e
          this.size++
      }
  }
  

3.3 LRU淘汰策略（最近最少使用淘汰策略）

• 问题：146. LRU 缓存 - 力扣（Leetcode）

• 分析

  • 有了上一题LRU的基础，这题已经不再困难了
  • 与LFU一样，我们需要用一个map结构来记录key和真实数据节点的映射关系，这样我们才能快速定位key对应的节点
  • 与LFU不同的是，LRU关注的是数据被访问的次序，而不关注数据被访问的频次，因此，LRU不会有LFU那种访问频率和访问次序需要兼顾的冲突。于是，我们只需要一个链表既可以保存所有数据节点
    • 我们将最近访问的节点通过头插法插入到链表头部
    • 这样，链表尾部的节点就是最近最少使用的数据，淘汰的时候从链表尾部淘汰即可
  • Get操作：通过map定位到节点的具体地址，获取数据后，将节点移动到链表头部
  • Put操作：若key已经存在，则修改value并将节点移动到链表头部，若key不存在，则判断是否需要淘汰，然后将新节点插入到链表头部即可

• 设计方案

  type entry struct{
      key interface{}
      value interface{}
  }
  
  type LRUCache struct{
      capacity int
      size int
      cache map[interface{}]*list.Element
      list *list.List
  }
  
  func NewLRUCache(cap int)*LRUCache{
      return LRUCache{
          capacity:cap,
          size:0,
          cache:make(map[interface{}]*list.Element),
          list:list.New(),
      }
  }
  
  func (this *LRUCache)Get(key interface{}){
      if this.size == 0{
          return -1
      }
      if ele,ok := this.cache[key];ok{
          this.list.MoveToFront(ele)
          return ele.Value.(*entry).value
      }
      return -1
  }
  
  func (this *LRUCache)Put(key,value interface{}){
      if this.capacity == 0{
          return
      }
      if ele,ok := this.cache[key];ok{
          ele.Value.(*entry).value = value
          this.list.MoveToFront(ele)
      }else{
          if this.size == this.capacity{
              e := this.list.Back()
              Value := this.list.Remove(e)
              this.cache = delete(this.cache,Value.(*entry).key)
              this.size--
          }
          entry := &entry{
              key:interface{},
              value:interface{},
          }
          e := this.list.PushFront(entry)
          this.cache[key] = e
          this.size++
      }
  }
  

3.4 跳表

• 问题：1206. 设计跳表 - 力扣（Leetcode）

• 分析

  • 跳表的数据结构如下所示

• 跳表的理解：我们知道，当遇到有序无重复的数组时，我们可以使用二分法快速地在数组中插入，或者查询某个数据，这是因为数组是顺序结构，支持通过下标随机查找地原因。相对而言，对于一个有序链表来讲，即使元素有序，我们要查询某个数据时，依然得从链表头顺序遍历查找，那有没有什么办法能让有序链表拥有二分查找地功能呢？简单的做法就是给跳表中的节点添加索引，通过添加多层索引，我们就可以有效降低链表查找的时间复杂度。这就是跳表的原理

  • 学过mysql底层的可能已经发现，这个跳表的原理怎么这么像B+树，没错，B+树也是通过给主键添加索引来构造的多路平衡搜索树，这两个数据结构都能快速的查找有序节点，且能做到范围查找，但是B+树的时间复杂度是O(h*logn)，h为树的高度，而跳表的时间复杂度为O(logn)。此外，B+树更适合用于磁盘数据管理，因为树的高度决定了访问磁盘IO的次数，而跳表则更适合管理内存数据，比如redis中zset的底层结构就是跳表。

• 跳表的查询

  • 跳表和B+树相似，只有最底层的链表会保存所有的数据，而上层的节点都只是保存索引而已，因此，当要查询某个数据时，跳表的最终目的都是找到最底层的链表节点。
  • 当查询某个key时，首先从跳表的最上层索引开始查找，找到比key小但是最接近key的一个索引节点后，继续往下一层查找，在每一层都找到一个小于key但是最接近与key的节点，直到找到最后一层。
  • 由于最后一层是一个有序单链表，因此，我们只需要判断下一个节点是不是我们要找的key即可

• 跳表的插入

  • 在跳表插入num之前，首先要找到num应该插入的位置，由于我们的数据只保存在最底层链表，因此我们首先也要通过跳表的查询功能，找到比num小但最接近num的底层节点位置，然后把num插入在该节点的后面

  • 如果只是单纯的在链表底层插入一个节点，那么跳表的结构就显得很多余了，我们在创建节点时，还必须在上层索引中添加对应的索引！那什么时候才添加索引呢？在哪一层添加索引呢？跳表的设计者给出了一个概率公式，即当跳表节点足够多的时候，跳表的底层节点在每一层以P的概率出现的时候，总的时间复杂度是趋于稳定的。

    • 我们假设这个P是1/2，即底层某个节点在第一层索引出现的概率是1/2，在第二层索引出现的概率就是1/2*1/2=1/4。（因为跳表规定，上层索引出现的节点，在下层必须出现）

    • 因此，我们在插入一个节点后，还要根据概率给该节点生成一个索引层数，根据这个索引层数来在上层索引中插入节点。以概率P=1/2为例，我们想象一下抛硬币，正面为0，反面为1.在插入一个节点后，我们开始抛硬币，直到抛出正面为止，记录抛硬币的次数就是我们的索引层数。

      • 假设我们抛了一次硬币就是正面，那么我们的索引层数就为1，即我们不需要在上面创建索引了。
      • 假设我们抛了3次硬币，即我们索引层次为3，那么我们不仅要在最底层插入节点，我们还需要在上两层索引中同样插入该节点作为索引节点

    • 综上所述，我们插入节点时首先要找到底层节点的插入位置，然后插入底层节点，再构造上层索引。那么还有一个问题，就是我们在前面已经通过跳表一层一层跳到底层了，又怎么回去上面层次插入索引呢？难道又从头开始跳？当然，我们可以选择空间换时间的方法。

      • 我们在每一层搜索时，都是找到一个比num小但最接近nun节点的位置，再往下跳的，当我们要在这一层插入以num为索引的节点时，那么num肯定是插在这个往下跳的节点的后面，因此，我们在每一层往下跳的时候，将这个节点保存起来，每一层都保留最接近的节点。在最后构造索引的时候，我们根据索引的层次拿出对应的节点，在他们后面插入索引就可以了

  • 跳表的删除

    • 与跳表的插入操作是相似的，在每一层中找到一个小于target且最接近target的节点，将该节点保存下来，然后往下跳，一直找到最底层。随后在底层判断下一个节点是不是target，是的话就从底层中删除target。
    • 从底层删除target后，我们还要从上层索引删除target，我们无法知道当前target有多少层索引，因此我们可以从最底层往上一直到跳表的最高层，通过判断我们保存下来的节点的下一个节点，如果是target就一次删除即可
    • 同时还要注意，有可能我们删除的target是在最上层索引的，而且最上层索引只有target一个节点，在我们删除了target后，最上层索引就没有了，因此跳表的索引层次就需要减1。因此，我们每次删除节点后，还要维护一下跳表的索引层级

• 跳表设计

  • 结构定义

  const MaxLevel = 32 // 跳表的最大层次
  const P = 0.5 // 定义节点出现在每一层的概率
  
  type Node struct{
      Val int // 存放数据
      Forward []*Node //由于每个节点都有可能成为上层索引，我们并不知道某个节点究竟有几层索引，因此就用一个切片来存放指针，Forward[i]表示的是当前节点在第i层指向的下一个节点的地址
  }
  
  type SkipList struct{
      Head *Node // 虚拟头节点，便于节点的插入删除操作
      Level int // 记录当前跳表的最大索引层数
  }
  
  func NewSkipList()*SkipList{
      return &SkipList{
          Head:&Node{
              Val:-1,
              Forward:make([]*Node,MaxLevel) // 由于不知道每个节点的层次，因此直接开到最大层次，通过Level字段保存最大的层次即可。
          },
          Level:0,
      }
  }
  

  • 跳表搜索

  func (s *SkipList)Search(target int)bool{
      cur := s.Head // 从虚拟头节点开始查找
      for i := s.Level-1 ; i >= 0 ; i--{ // 从当前跳表的最上层索引开始查找
          for cur.Forward[i] != nil && cur.Forward[i].Val < target{ // 在第i层中找到比target小且最接近target的节点
              cur = cur.Forward[i]
          }
      }
      cur = cur.Forward[0] // 从for循环出来时，cur此时一定指向了最接近target的值，我们获取其最底层的下一个节点
      return cur != nil && cur.Val == target
  }
  

  • 跳表插入

  func (s *SkipList)Add (num int){
      update := make([]*Node,MaxLevel) // 用于记录每一层比num小且最接近num的节点，便于后续 插入索引
      cur := s.Head
      
      for i := range update{ //这步初始化是必须的，因为新插入的节点层次可能比现有节点层次高，而update保存的是最接近num的节点，当新节点层次比现有层次高时，相当于在最上层再开索引，那么此时最接近num的节点就是头节点
          update[i] = s.Head
      }
      
      for i := s.Level - 1;i >= 0;i--{
          for cur.Forward[i] != nil && cur.Forward[i].Val < num{
              cur = cur.Forward[i]
          }
          update[i] = cur // 记录第i层中比num小但最接近num的节点
      }
      
      lv := RandomLevel() // 通过随机算法获取新节点的索引层次
      s.Level = max(s.Level,lv) // 如果新节点的层次比跳表最高层还大，说明要再建一层上层索引，因此修改跳表索引层次
      
      newNode := &Node{ // 构造新节点
          Val:num,
          Forward:make([]*Node,lv) // 只会在第0-第(lv-1)层存在索引
      }
      
      for i,node := range update[:lv]{ // 从第0层开始，一直到(lv-1)层，依次插入新节点
          newNode.Forward[i] = node.Forward[i]
          node.Forward[i] = newNode
      }
  }
  
  func RandomLevel()int{
      lv := 1
      for lv < MaxLevel && rand.Float64() < P{
          lv++
      }
      return lv
  }
  
  func max (a,b int)int{
      if a > b {
          return a 
      }
      return b
  }
  

  • 跳表的删除

  func (s *SkipList) Erase(num int)bool{
      update := make([]*Node,MaxLevel)
      cur := s.Head
      
      // 注意，这里和Add不一样的地方在于，我们不需要初始化update了，因为我们在删除节点的时候不可能会比原来的层次更小了，如果某一层的update为nil，说明这一层根本不存在节点，更不需要删除节点了
      
      for i:=s.Level-1;i >= 0;i--{
          for cur.Forward[i] != nil && cur.Forward[i].Val < num{
              cur = cur.Forward[i]
          }
          update[i] = cur
      }
      
      cur = cur.Forward[0]
      
      if cur == nil || cur.Val != num{ // 说明跳表中根本不能存在num
          return false
      }
      
      // 由于我们不知道删除的num在那一层存在着索引，因此我们从第0层开始，一直到当前跳表的最高层，依次寻找节点num进行删除即可
      for i:=0;i<s.Level && update[i].Forward[i] == cur;i++{
          update[i].Forward[i] = cur.Forward[i]
      }
      
      // 最后，我们来维护一下当前跳表的最大层次
      for this.Level > 1 && this.Head.Forward[this.Level-1] == nil{
          this.Level--
      }
      return true
  }