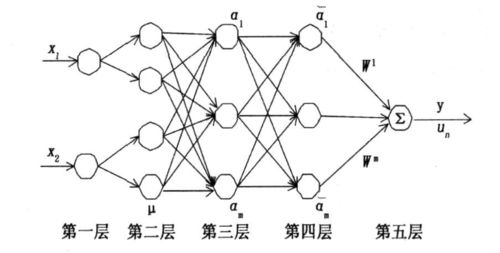
神经网络模型参考自适应,神经网络自适应控制
简单介绍人工神经网络和模糊神经网络
其实百科介绍的很详细,如“人工神经网络是模拟人脑结构的思维功能,具有较强的自学习和联想功能,人工干预少,精度较高,对专家知识的利用也较少。
但缺点是它不能处理和描述模糊信息,不能很好利用已有的经验知识,特别是学习及问题的求解具有黑箱特性,其工作不具有可解释性,同时它对样本的要求较高;模糊系统相对于神经网络而言,具有推理过程容易理解、专家知识利用较好、对样本的要求较低等优点,但它同时又存在人工干预多、推理速度慢、精度较低等缺点,很难实现自适应学习的功能,而且如何自动生成和调整隶属度函数和模糊规则,也是一个棘手的问题。
”即保证人工神经网络自身的学习能力下,采用模糊理论解决模糊信号,使神经网络权系数为模糊权,或者输入为模糊量。
比如原本神经网络处理的是连续数据(double)不适合求解模糊数据,此时就需要引入模糊理论,来构造适合于求解这类模糊数据的神经网络。
从人工智能模拟自然界的角度,请简述模糊控制和人工神经网络的区别?
bp神经网络就是模糊神经网络吗
自组织神经网络与模糊控制有什么优点
(2)由工业过程的定性认识出发,比较容易建立语言控制规则,因而模糊控制对那些数学模型难以获取,动态特性不易掌握或变化非常显著的对象非常适用。
(3)基于模型的控制算法及系统设计方法,由于出发点和性能指标的不同,容易导致较大差异;但一个系统语言控制规则却具有相对的独立性,利用这些控制规律间的模糊连接,容易找到折中的选择,使控制效果优于常规控制器。
(4)模糊控制是基于启发性的知识及语言决策规则设计的,这有利于模拟人工控制的过程和方法,增强控制系统的适应能力,使之具有一定的智能水平。
(5)模糊控制系统的鲁棒性强,干扰和参数变化对控制效果的影响被大大减弱,尤其适合于非线性、时变及纯滞后系统的控制。|||什么是模糊控制?与传统控制理论相比有什么优点?
模糊控制是近代控制理论中建立在模糊集合轮上基础上的一种基于语言规则与模糊推理的控制理论,它是智能控制的一个重要分支。
与传统控制理论相比,模糊控制有两大不可比拟的优点:第一,模糊控制在许多应用中可以有效且便捷的实现人的控制策略和经验,这一优点自从模糊控制诞生以来就一直受到人们密切的关注;第二,模糊控制不需要被控对象的数学模型即可实现较好的控制,这是因为被控对象的动态特性已隐含在模糊控制器输入、输出模糊集及模糊规则中。
所以模糊控制被越来越多的应用于各个领域,尤其是被广泛应用于家电系列中,基于模糊控制的洗衣机就是其中的一个典型实例。|||模糊控制实质上是一种非线性控制,从属于智能控制的范畴。
模糊控制的一大特点是既具有系统化的理论,又有着大量实际应用背景。|||优点:对于难于建立模型的控制对象不失为一种良好的控制方法。
数据挖掘中的神经网络和模糊逻辑的概念是啥?
。
【神经网络】人工神经网络(ArtificialNeuralNetworks,简写为ANNs)也简称为神经网络(NNs)或称作连接模型(ConnectionModel),它是一种模仿动物神经网络行为特征,进行分布式并行信息处理的算法数学模型。
这种网络依靠系统的复杂程度,通过调整内部大量节点之间相互连接的关系,从而达到处理信息的目的。最常用的就是BP神经网络了,你做数据挖掘SVM也很常用。
【模糊】模糊逻辑指模仿人脑的不确定性概念判断、推理思维方式,对于模型未知或不能确定的描述系统,以及强非线性、大滞后的控制对象,应用模糊集合和模糊规则进行推理,表达过渡性界限或定性知识经验,模拟人脑方式,实行模糊综合判断,推理解决常规方法难于对付的规则型模糊信息问题。
模糊逻辑善于表达界限不清晰的定性知识与经验,它借助于隶属度函数概念,区分模糊集合,处理模糊关系,模拟人脑实施规则型推理,解决因“排中律”的逻辑破缺产生的种种不确定问题。
粗糙集(Roughset,也称粗集)理论是波兰学者2.Pawlak于1982年提出的,它为处理不确切的!不完整的信息提供了一种新的数学工具。
粗糙集理论建立在分类机制的基础之上,将分类理解为特定空间上的等价关系,而等价关系构成了对该空间的划分。该理论将知识理解为对数据的划分,每一划分的集合称为概念。
粗糙集理论的主要思想是在保持信息系统分类能力不变的前提下,利用己知的知识库,将不精确或不确定的知识用知识库中己有的知识来近似刻画,通过知识的补充!约简,导出问题的决策或分类规则。
粗糙集理论与其它处理不确定和不精确问题理论最显著的区别是粗糙集理论无须提供问题所需处理的数据集合之外的任何先验信息,对问题的不确定性的描述或处理比较客观,又由于这个理论未包含处理不精确或不确定原始数据的机制,所以该理论与概率论!模糊数学!证据理论等其它处理不精确或不确定问题的理论有很强的互补性。
粗糙集理论不仅为信息科学和认知科学提供了新的研究方法,而且为智能信息处理提供了有效的处理技术。
目前粗糙集理论己经是人工智能领域方面的一个研究热点,成为数据挖掘应用的主要技术之一,受到各国学者的高度重视。
人工神经网络有哪些类型
人工神经网络模型主要考虑网络连接的拓扑结构、神经元的特征、学习规则等。目前,已有近40种神经网络模型,其中有反传网络、感知器、自组织映射、Hopfield网络、波耳兹曼机、适应谐振理论等。
根据连接的拓扑结构,神经网络模型可以分为: