5、电路综合-超酷-基于S11参数直接综合出微带线电路图

电路综合-超酷-基于S11参数直接综合出微带线电路图

1、电路综合原理与实践—电抗函数的综合原理
2、电路综合原理与实践—正实函数与策动电阻抗函数
3、电路综合原理与实践—单双端口理想微带线（伪）手算S参数与时域波形

之前已经介绍过如何通过电路的微带线结构求解得到其S参数（3、电路综合原理与实践—单双端口理想微带线（伪）手算S参数与时域波形），下面介绍一种特别酷的东西，从微带线的S11参数得到可以将其实现的结构。

从S11参数直接得到微带线电路图是一种叫简化实频的技术，可以用于匹配电路的设计，例如我需要在1GHz将10欧姆匹配至50欧姆，只需要控制1GHz的S11参数在10欧姆处就行（需要先将S参数转化为Z参数）。

1、理查德域S11参数的表达式

此处的S11的参数表达式为理查德域的，可能和我们平时见到的S11的图像一样的格式不太一致，如：

那么这个式子究竟代表了什么呢？对于无耗的传输线，其可以表达为如下的形式：

其中beta为相移常数，l为微带线的实际的长度。在下面的分析中，我使用电长度这种间接的表达方法来示意。例如，在1GHz下的电长度为60°的微带线的实际长度为l=ele_l/360*c/f。其中ele_l为电长度（60，单位度），c为光速，f为该电长度所在的频率（1GHz）。

此外，beta=beta=2* pi *freq_solve/c，其中freq_solve为求解的频率（也就是要求解哪个频率的S参数）。这样，对应一个固定的表达式，其S11参数会随着频率发生变化，此外因为lamda是周期函数，最后得到的S11参数也必定是周期的。

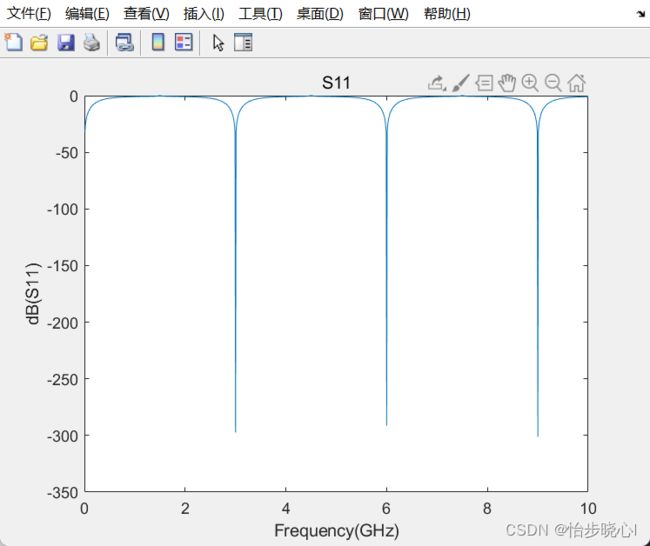
对于上面的S11表达式，使用如下的程序绘制其对应的S11参数（其中微带线使用的是1GHz下60度电长度的微带线，对应的实际长度为0.05m，忽略介电常数等等）：

clear
close all
clc
%微带线电长度
ele_l=60;
%微带线电长度所在的频率
f=1e9;
%求解频率范围，单位GHz
f_start=0.01;
f_stop=10;
f_step=0.01;

%光速
c=299792458;
%求解范围
freq_solve=[f_start:f_step:f_stop]*1e9;
%计算物理长度，单位m
l=ele_l/360*c/f;
%计算不同频率下的相移常数beta
beta=2*pi*freq_solve/c;
%转换到lamda域
lamda=1j*tan(beta*l);

S11=(lamda.^2+19*lamda)./(lamda.^2+21*lamda+8);

figure
plot(freq_solve/1e9,20*log10(abs(S11)))
xlabel('Frequency(GHz)')
ylabel('dB(S11)')
title('S11')

得到的图片如下所示：

2、求解理论过程

STEP0:
以上面案例为例：

结合：

进而：

k=1代表级联微带线数为1。

STEP1：把lamda=1带入S11表达式：

STEP2：计算Zi：

STEP3：计算K：

STEP4：计算S：


STEP5：计算下一级S：

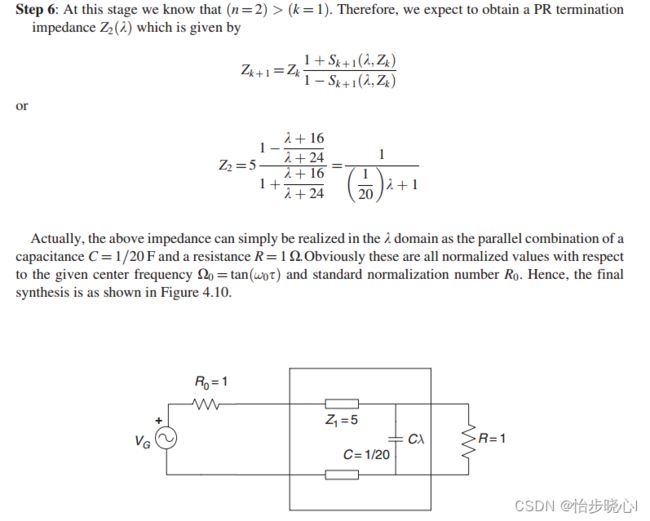
STEP6：计算阻抗：

3、电路生成 案例1—开路微带线综合

在更加一般的情况，我们是基于第一部分最后一张图的S11参数去设计匹配电路。我们可以利用S11参数去反推表达式。在此给出一个示例（使用第一部分的表达式为案例）：

clear
clc
syms lamda
S11=(lamda.^2+19*lamda)./(lamda.^2+21*lamda+8);
Zin=(1+S11)/(1-S11);

S11_Z0=S11;
Z0=1;
ind=1;

s11_tmp(ind)=subs (S11_Z0,Z0);
for cnt=1:1:2
    if ind==1
        Z(ind)=Z0*(1+s11_tmp(ind))/(1-s11_tmp(ind));
        K(ind)=(Z0-Z(ind))/(Z0+Z(ind));
        S11_Zi(ind)=(K(ind)+S11_Z0)/(1+K(ind)*S11_Z0);
        S111_Zi(ind)=simplify(S11_Zi(ind)*(1+lamda)/(1-lamda));
        ind=ind+1;
    else
        Z(ind)=simplify(Z(ind-1)*(1+S111_Zi(ind-1))/(1-S111_Zi(ind-1)))
        Z(ind)=subs (Z(ind),Z0);
        K(ind)=(Z(ind-1)-Z(ind))/(Z(ind-1)+Z(ind));
        S11_Zi(ind)=(K(ind)+S111_Zi(ind-1))/(1+K(ind)*S111_Zi(ind-1));
        S111_Zi(ind)=simplify(S11_Zi(ind)*(1+lamda)/(1-lamda));
        ind=ind+1;
    end
end
Z

运行结果如下所示：

表示该阻抗可以使用两个部分组成，第一部分为阻抗为5欧姆的微带线，第二部分为电容和电阻的并联：


依据解析结果，构建如下的电路原理图：

运行仿真，仿真结果与理论分析结果一致：

4、电路生成 案例2—基于策动点阻抗函数综合多微带电路

要综合的输入阻抗函数如下所示（此处t就是lamda）：

%                100*t^3 + 50*t^2 + 300*t + 30
%		Z(t) = -------------------------------	
%                9*t^3 + 170*t^2 + 31*t + 30

绘制其对应的S11参数和Zin参数曲线（假定使用频率1GHz下电长度60度的微带线进行实现），使用如下代码：

clear
close all
clc
%微带线电长度
ele_l=60;
%微带线电长度所在的频率
f=1e9;
%求解频率范围，单位GHz
f_start=0.01;
f_stop=10;
f_step=0.01;

%光速
c=299792458;
%求解范围
freq_solve=[f_start:f_step:f_stop]*1e9;
%计算物理长度，单位m
l=ele_l/360*c/f;
%计算不同频率下的相移常数beta
beta=2*pi*freq_solve/c;
%转换到lamda域
lamda=1j*tan(beta*l);

Zin=(100*lamda.^3+50*lamda.^2+300*lamda+30)./(9*lamda.^3+170*lamda.^2+31*lamda+30);
S11=(Zin-1)./(Zin+1);

figure
plot(freq_solve/1e9,(abs(Zin)))
xlabel('Frequency(GHz)')
ylabel('Zin')
title('Zin')

figure
plot(freq_solve/1e9,20*log10(abs(S11)))
xlabel('Frequency(GHz)')
ylabel('dB(S11)')
title('S11')

得到的S11参数和Zin参数结果如下所示：

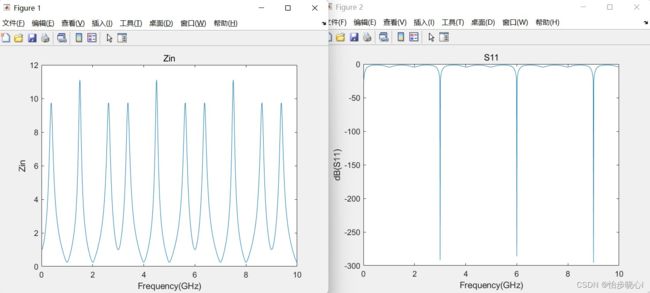
使用下面代码进行综合：

clear
clc
syms lamda

Zin=(100*lamda.^3+50*lamda.^2+300*lamda+30)./(9*lamda.^3+170*lamda.^2+31*lamda+30);
S11=(Zin-1)./(Zin+1);


S11_Z0=S11;
Z0=1;
ind=1;

s11_tmp(ind)=subs (S11_Z0,Z0);
for cnt=1:1:4
    if ind==1
        Z(ind)=Z0*(1+s11_tmp(ind))/(1-s11_tmp(ind));
        K(ind)=(Z0-Z(ind))/(Z0+Z(ind));
        S11_Zi(ind)=(K(ind)+S11_Z0)/(1+K(ind)*S11_Z0);
        S111_Zi(ind)=simplify(S11_Zi(ind)*(1+lamda)/(1-lamda));
        ind=ind+1;
    else
        Z(ind)=simplify(Z(ind-1)*(1+S111_Zi(ind-1))/(1-S111_Zi(ind-1)))
        Z(ind)=subs (Z(ind),Z0);
        K(ind)=(Z(ind-1)-Z(ind))/(Z(ind-1)+Z(ind));
        S11_Zi(ind)=(K(ind)+S111_Zi(ind-1))/(1+K(ind)*S111_Zi(ind-1));
        S111_Zi(ind)=simplify(S11_Zi(ind)*(1+lamda)/(1-lamda));
        ind=ind+1;
    end
end
Z

运行结果如下：

构建ADS仿真验证：

结果一致：