DS线性表之栈和队列
前言
我们前面已经介绍并实现了顺序表和链表以及介绍了他们的优缺点!本期我们再来学习一个基本数据结构栈和队列~!这里的栈可不是内存的那个栈,内存的那个栈是操作系统的概念,而这个栈是数据结构的栈,是一个容器。他们是两个不同学科的概念不要混淆了!!!
本期内容介绍
栈的概念和分类
顺序栈的实现
链式栈的实现
队列的概念和分类
链式队列的实现
循环队列的实现
目录
前言
本期内容介绍
一、栈的概念和分类
二、顺序栈的实现
栈的申明
初始化
销毁
入栈
出栈
获取栈顶元素
获取栈的有效元素个数
判断是否为空
三、链式栈的实现
链式栈的申明
创建一个新节点
销毁
入栈
出栈
获取栈顶元素
判断栈是否为空
获取栈的有效元素个数
全部源码:
四、队列的概念和分类
五、链式队列的实现
队列的申明
初始化
销毁
开一个新节点
入队列
出队列
获取队头元素
获取队尾数据
判断是否为空
获取队列元素个数
全部源码:
六、循环队列的实现
循环队列的申明
初始化
销毁
判断是否为空
判断是否已满
入队列
删除
获取元素的个数
获取队头数据
获取队尾的数据
一、栈的概念和分类
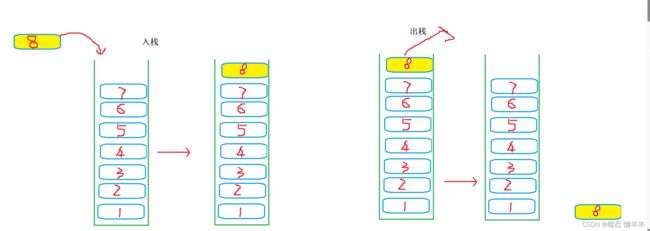
栈(stack):是一种特殊的线性表。只允许在固定的一端进行插入和删除操作的数据结构。进行插入和删除操作的那一端被称作栈顶,另一端被称作栈底!栈的特点是后进先出(LIFO),即后入栈的数据先出来!根据实现方式可以分为顺序栈和链式栈~!
压栈(入栈):栈的插入操作叫做压栈/入栈/进栈。
出栈:栈的删除操作叫做出栈。
入栈和出栈都在栈顶!
什么意思呢?你可能没有太明白,我来画张图理解一下:
二、顺序栈的实现
栈的实现可以用数组也可以使用链表,我们先来用数组来实现,也就是顺序栈!顺序栈又可分为静态和动态的,我们前面顺序表以及通讯录介绍了静态的版本几乎没用,很不实用。所以这里我们还是采用动态版本!非要静态版的话,就在他满的时候不要插了(入栈)!!!
静态版本栈的定义:
//栈的静态定义
typedef int STDataType;
#define N 100
struct Stack
{
STDataType a[N];
int top;//栈顶
};栈的申明
//栈的都动态定义
typedef int STDataType;
typedef struct Stack
{
STDataType* a;
int top;//栈顶
int capacity;//容量
}ST;
初始化
//初始化
void STInit(ST* ps)
{
assert(ps);
ps->a = NULL;
ps->top = ps->capacity = 0;
}销毁
//销毁
void STDestory(ST* ps)
{
assert(ps);
free(ps->a);
STInit(ps);
}入栈
//入栈
void STPush(ST* ps, STDataType x)
{
assert(ps);
//判断扩容
if (ps->capacity == ps->top)
{
int newcapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;
STDataType* tmp = (STDataType*)realloc(ps->a, sizeof(STDataType) * newcapacity);
if (tmp == NULL)
{
perror("malloc failed");
exit(-1);
}
ps->a = tmp;
ps->capacity = newcapacity;
}
//插入
ps->a[ps->top++] = x;
}出栈
//出栈
void STPop(ST* ps)
{
assert(ps);
assert(ps->top > 0);//空
ps->top--;
}获取栈顶元素
//获取栈顶元素
STDataType STTop(ST* ps)
{
assert(ps);
assert(ps->top > 0);//空
return ps->a[ps->top - 1];
}获取栈的有效元素个数
//获取栈的有效元素个数
int STSize(ST* ps)
{
return ps->top;
}判断是否为空
//是否为空
bool IsEmpty(ST* ps)
{
assert(ps);
return ps->top == 0;
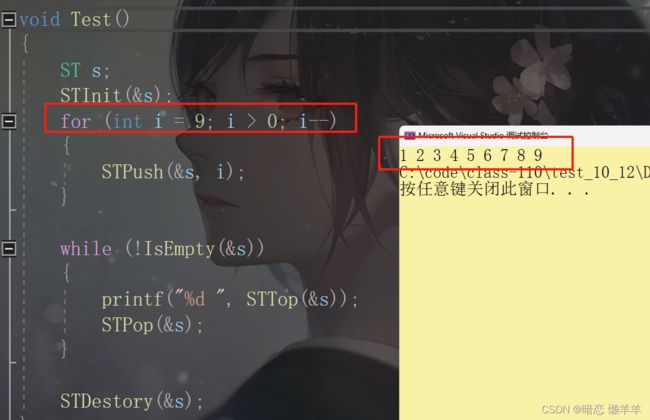
}OK,这块前面已经写过多次了,就不在多赘述了~!下面我们来测试一把:
#include "Stack.h"
void Test()
{
ST s;
STInit(&s);
for (int i = 9; i > 0; i--)
{
STPush(&s, i);
}
while (!IsEmpty(&s))
{
printf("%d ", STTop(&s));
STPop(&s);
}
STDestory(&s);
}
int main()
{
Test();
return 0;
}是不是符合后进先出啊!下面我们在来实现链式栈!
三、链式栈的实现
栈的另一种实现方式就是用单链表,当然带不带头都可以!我们这里选择不带头的,如果不带头的能搞定带头的那就是小卡拉米~!由于栈的特点(后进先出),再结合单链表的特点头插头删效率很高,所以我们采用单链表的头来当栈顶,单链表的尾为栈底。
链式栈的申明
typedef STDataType;
typedef struct Stack
{
STDataType data;
struct Stack* next;
}ST;创建一个新节点
其实这里和单链表那里一样可以不初始化的。我们直接进行其他操作!
//创建一个新节点
ST* BuyNode(STDataType x)
{
ST* newnode = (ST*)malloc(sizeof(ST));
if (newnode == NULL)
{
perror("malloc failed");
exit(-1);
}
newnode->data = x;
newnode->next = NULL;
return newnode;
}销毁
//销毁栈
void STDestory(ST** head)
{
assert(head);
ST* cur = *head, * tail = NULL;
while (cur)
{
tail = cur->next;
free(cur);
cur = tail;
}
*head = NULL;
}入栈
//插入
void Push(ST** head, STDataType x)
{
assert(head);
ST* node = BuyNode(x);
node->next = *head;
*head = node;
}出栈
//出栈
void Pop(ST** head)
{
assert(head);
assert(*head);//栈为空的情况
ST* del = *head;
*head = (*head)->next;
free(del);
}获取栈顶元素
//获取栈顶的元素
STDataType STTop(ST* head)
{
assert(head);
return head->data;
}判断栈是否为空
//是否为空
bool STEmpty(ST* head)
{
return head == NULL;
}
获取栈的有效元素个数
//获取栈的有效元素个数
int STSize(ST* head)
{
int size = 0;
while (head)
{
++size;
head = head->next;
}
return size;
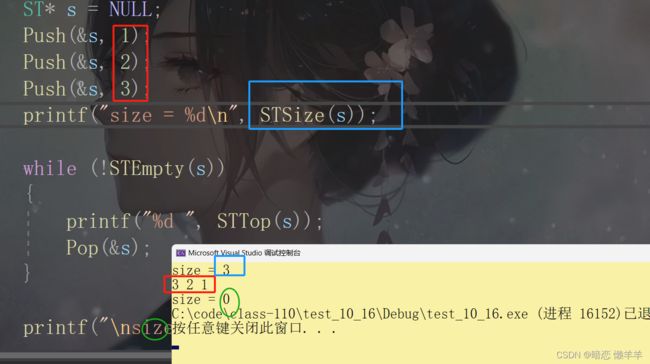
}OK测试一下:
#include "Stack.h"
void Test()
{
ST* s = NULL;
Push(&s, 1);
Push(&s, 2);
Push(&s, 3);
printf("size = %d\n", STSize(s));
while (!STEmpty(s))
{
printf("%d ", STTop(s));
Pop(&s);
}
printf("\nsize = %d ", STSize(s));
STDestory(&s);
}
int main()
{
Test();
return 0;
}OK,是不是实现了~!其实这里就是新瓶装旧酒~!下面我们来一起看看另一个数据结构队列~!
全部源码:
#include
#include
#include
#include
typedef STDataType;
typedef struct Stack
{
STDataType data;
struct Stack* next;
}ST;
//创建一个新节点
ST* BuyNode(STDataType x);
//销毁栈
void STDestory(ST** head);
//入栈
void Push(ST** head, STDataType x);
//出栈
void Pop(ST** head);
//获取栈顶的元素
STDataType STTop(ST* head);
//是否为空
bool STEmpty(ST* head);
//获取栈的有效元素个数
int STSize(ST* head); #include "Stack.h"
//创建一个新节点
ST* BuyNode(STDataType x)
{
ST* newnode = (ST*)malloc(sizeof(ST));
if (newnode == NULL)
{
perror("malloc failed");
exit(-1);
}
newnode->data = x;
newnode->next = NULL;
return newnode;
}
//销毁栈
void STDestory(ST** head)
{
assert(head);
ST* cur = *head, * tail = NULL;
while (cur)
{
tail = cur->next;
free(cur);
cur = tail;
}
*head = NULL;
}
//入栈
void Push(ST** head, STDataType x)
{
assert(head);
ST* node = BuyNode(x);
node->next = *head;
*head = node;
}
//出栈
void Pop(ST** head)
{
assert(head);
assert(*head);//栈为空的情况
ST* del = *head;
*head = (*head)->next;
free(del);
}
//获取栈顶的元素
STDataType STTop(ST* head)
{
assert(head);
return head->data;
}
//是否为空
bool STEmpty(ST* head)
{
return head == NULL;
}
//获取栈的有效元素个数
int STSize(ST* head)
{
int size = 0;
while (head)
{
++size;
head = head->next;
}
return size;
}#include "Stack.h"
void Test()
{
ST* s = NULL;
Push(&s, 1);
Push(&s, 2);
Push(&s, 3);
printf("size = %d\n", STSize(s));
while (!STEmpty(s))
{
printf("%d ", STTop(s));
Pop(&s);
}
printf("\nsize = %d ", STSize(s));
STDestory(&s);
}
int main()
{
Test();
return 0;
}四、队列的概念和分类
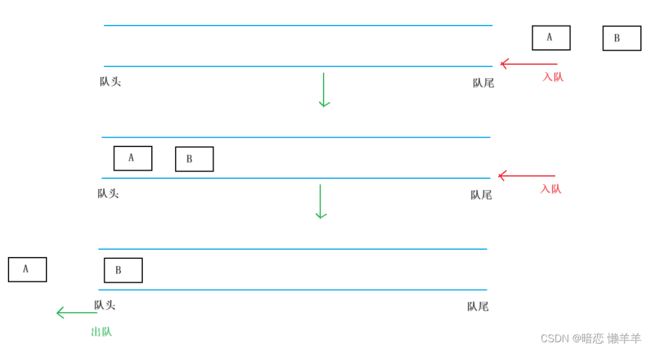
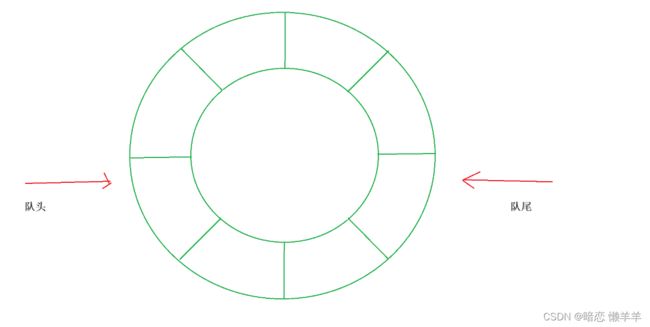
队列(Queue)也是一种特殊的线性表,他只允许在固定的一段进行插入(入队列),另一端进行删除(出队列)。插入的那一端叫做队尾,删除的那一端叫做队头~!队列的特点是先进先出(和你排队买饭的一样,先来的先买)! 队列的实现也分为数组和链式,当然数组的删除效率不高所以一般采用链式队列,但数组队列有一个很好的结构 ---- 循环队列,我们也会来实现的!
OK,还是来画个队列的图 ,大概先来认识一下:
这就是队列操作的一个过程~!我们下面来实现一下~!
五、链式队列的实现
上面也谈到了用数组实现的话删除(出队列)效率低,所以我们这里采用链表实现,用哪种链表实现呢?其实这里最好的是单链表(带不带头都行),你可能说要找尾进行入队列,所以双向循环较好,但我想说的是单链表给一个尾指针不也能很好的解决这个问题吗?所以这里做最好的解决方案是用单链表+一个尾指针实现~!
队列的申明
typedef int QDataType;
typedef struct QListNode
{
QDataType data;
struct QListNode* next;
}QNode;由于考虑到插入删除的时候得传二级指针,相对稍微麻烦一点,所以这里既要控制队头也要记录队尾,我们不妨在来一个结构体,里面成员是队头指针和队尾指针,这样做的好处就是不用传二级指针了,要改变队头指针的值只需要传结构体的指针即可~!为了获取队列中的数据我们这里还可以加一个size !
typedef struct Queue
{
QNode* head;
QNode* tail;
int size;
}Queue;初始化
//初始化
void QInit(Queue* p)
{
assert(p);
p->head = p->tail = NULL;
p->size = 0;
}销毁
//销毁
void QDestory(Queue* p)
{
assert(p);
QNode* cur = p->head, *next = NULL;
while (cur)
{
next = cur->next;
free(cur);
cur = next;
}
p->head = p->tail = NULL;
p->size = 0;
}开一个新节点
//开一个新节点
QNode* BuyNode(QDataType x)
{
QNode* newnode = (QNode*)malloc(sizeof(QNode));
if (newnode == NULL)
{
perror("malloc failed");
exit(-1);
}
newnode->data = x;
newnode->next = NULL;
return newnode;
}入队列
//入队列
void QPush(Queue* p, QDataType x)
{
assert(p);
QNode* node = BuyNode(x);
if (p->head == NULL)
{
p->head = p->tail = node;
}
else
{
p->tail->next = node;
p->tail = node;
}
p->size++;
}出队列
//出队列
void QPop(Queue* p)
{
assert(p);
assert(p->head);
QNode* next = p->head->next;
free(p->head);
p->head = next;
p->size--;
}获取队头元素
//获取队列头的数据
QDataType QTop(Queue* p)
{
assert(p);
assert(p->size > 0);
return p->head->data;
}获取队尾数据
//获取队列尾的数据
QDataType QTail(Queue* p)
{
assert(p);
assert(p->size > 0);
return p->tail->data;
}判断是否为空
//是否为空
bool QEmpty(Queue* p)
{
assert(p);
return p->size == 0;
}获取队列元素个数
//获取队列的元素个数
int QSize(Queue* p)
{
assert(p);
return p->size;
}OK,测试一把:
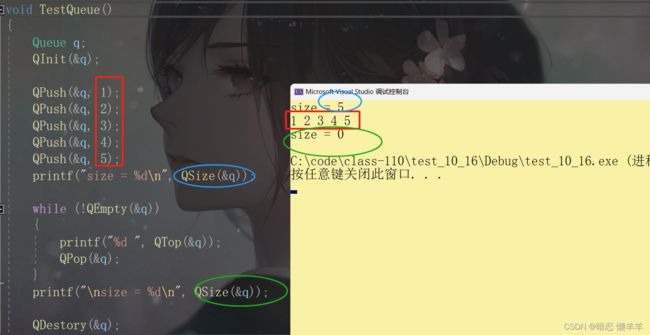
OK,实现了先进先出的特点!
全部源码:
#pragma once
#include
#include
#include
#include
typedef int QDataType;
typedef struct QListNode
{
QDataType data;
struct QListNode* next;
}QNode;
typedef struct Queue
{
QNode* head;
QNode* tail;
int size;
}Queue;
//初始化
void QInit(Queue* p);
//销毁
void QDestory(Queue* p);
//开一个新节点
QNode* BuyNode(QDataType x);
//入队列
void QPush(Queue* p, QDataType x);
//出队列
void QPop(Queue* p);
//获取队列头的数据
QDataType QTop(Queue* p);
//获取队列尾的数据
QDataType QTail(Queue* p);
//是否为空
bool QEmpty(Queue* p);
//获取队列的元素个数
int QSize(Queue* p);
#include "Queue.h"
//初始化
void QInit(Queue* p)
{
assert(p);
p->head = p->tail = NULL;
p->size = 0;
}
//销毁
void QDestory(Queue* p)
{
assert(p);
QNode* cur = p->head, *next = NULL;
while (cur)
{
next = cur->next;
free(cur);
cur = next;
}
p->head = p->tail = NULL;
p->size = 0;
}
//开一个新节点
QNode* BuyNode(QDataType x)
{
QNode* newnode = (QNode*)malloc(sizeof(QNode));
if (newnode == NULL)
{
perror("malloc failed");
exit(-1);
}
newnode->data = x;
newnode->next = NULL;
return newnode;
}
//入队列
void QPush(Queue* p, QDataType x)
{
assert(p);
QNode* node = BuyNode(x);
if (p->head == NULL)
{
p->head = p->tail = node;
}
else
{
p->tail->next = node;
p->tail = node;
}
p->size++;
}
//出队列
void QPop(Queue* p)
{
assert(p);
assert(p->head);
QNode* next = p->head->next;
free(p->head);
p->head = next;
p->size--;
}
//获取队列头的数据
QDataType QTop(Queue* p)
{
assert(p);
assert(p->size > 0);
return p->head->data;
}
//获取队列尾的数据
QDataType QTail(Queue* p)
{
assert(p);
assert(p->size > 0);
return p->tail->data;
}
//是否为空
bool QEmpty(Queue* p)
{
assert(p);
return p->size == 0;
}
//获取队列的元素个数
int QSize(Queue* p)
{
assert(p);
return p->size;
}void TestQueue()
{
Queue q;
QInit(&q);
QPush(&q, 1);
QPush(&q, 2);
QPush(&q, 3);
QPush(&q, 4);
QPush(&q, 5);
printf("size = %d\n", QSize(&q));
while (!QEmpty(&q))
{
printf("%d ", QTop(&q));
QPop(&q);
}
printf("\nsize = %d\n", QSize(&q));
QDestory(&q);
}
int main()
{
TestQueue();
return 0;
}六、循环队列的实现
循环队列也是很常见也很常用的一种队列,例如操作系统中有个模型叫“生产者和消费者”就用的是循环队列,当然他也可以用数组实现也可以用循环链表来实现!上面的使用链表实现的,我们这里用数组来实现~!
OK,开始之前还是来先画一个循环队列看看~!
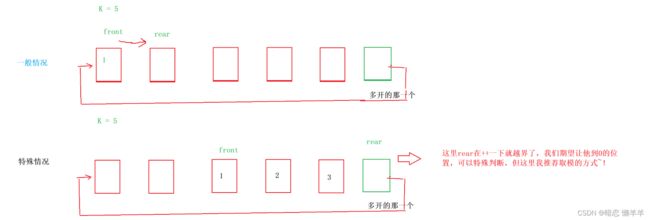
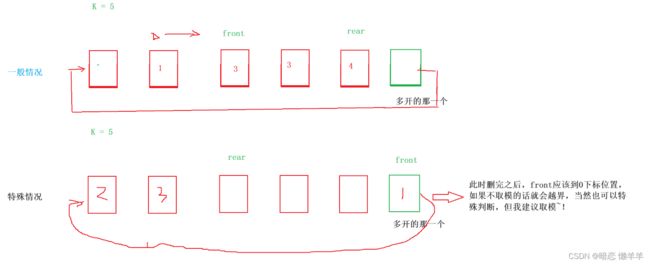
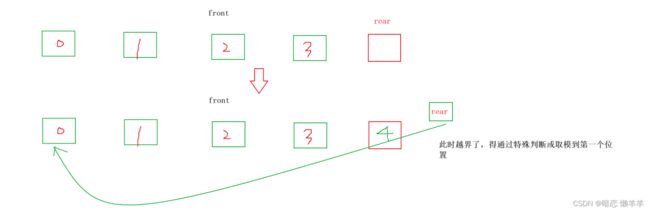
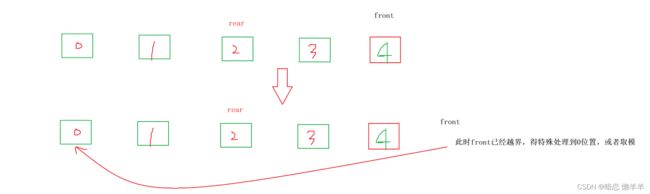
他这个是怎么玩的呢?他是把空间开好后用两个指针(front和rear(指向当前位置的下一个位置)下标)来控制的,插入就是覆盖rear指向的那个位置,然后rear向后移动1,不用挪动数据。删除也是一样让front++一下!这里你可能会问如何判空呢?当front == rear == 0?那啥时候判满呢?是不是不好弄啊!设计这种队列的人想到了一个办法是:多开一个空间把那个空间浪费掉,当rear == front时表示空,当rear + 1 == front时表示满,如果是数组实现的话你要让rear已经是最后一个的话你在加一是不是越界了!所以rear+1 %队列的长度就好了,这样当超过的时候就有回去了(见下图1),删除的时候也是一样要%个队列的长度(见图2)。OK大概就是这样,具体的细节我们实现的时候再解释~!
图1
图2
OK,我们来实现一下:
循环队列的申明
这里的类型申明有两种形式,一种是你直接给好数组的大小,一种是不确定大小得输入!
typedef int LQDataType;
#define MAX 5
typedef struct LQueNode
{
LQDataType a[MAX];
int front;//队头
int rear;//队尾
int size;//元素个数
}LQ;
typedef int LQDataType;
typedef struct LQueNode
{
LQDataType* a;
int front;//队头
int rear;//队尾
int k;//队列的大小
int size;
}LQ;第二种就是要在初始化的时候进行输入你的队列的大小!其实俩囊中相比较之下,后者更好一点,我就给予第二种来实现~!
初始化
这两种申明不同他们的初始化也不同,静态的只需要控制好front和rear就好,而动态的话不知道你要开多少个所以采用malloc,这个要记得free! 我在这里就演示一下出不同的初始化和销毁~!
静态初始化
//初始化
void LQInit(LQ* p,int k)
{
assert(p);
p->front = p->rear = 0;//这里可以是-1,可以是0,我们这里采用后者
p->size = 0;
}动态初始化
//初始化
void LQInit(LQ* p, int k)
{
assert(p);
p->a = (LQDataType*)malloc(sizeof(LQDataType) * k + 1);
p->front = p->rear = 0;
p->k = k;
p->size = 0;
}销毁
静态销毁
静态的只考虑把front和rear, size处理好即可,而动态版本的话要先free动态开的数组然后在处理其他的~!
//销毁
void LQDestory(LQ* p)
{
LQInit(p);
}动态销毁
//销毁
void LQDestory(LQ* p)
{
assert(p);
free(p->a);
p->front = p->rear = 0;
p->k = p->size = 0;
}判断是否为空
我们前面介绍过了,判断为空的条件是front == rear
//是否为空
bool IsEmpty(LQ* p)
{
assert(p);
return p->rear == p->front;
}判断是否已满
前面已经介绍了,为了区分满和空专门多开了一个空间,rear是当前元素的下一个位置,所以当rear+1%实际队列的长度 == front时就是满了~!
//是否为满
bool IsFull(LQ* p)
{
assert(p);
return (p->rear + 1) % (p->k + 1) == p->front;
}
入队列
由于这个队列的长度是固定的,所以你在插入即入队列时得先判断是否为满,满了就不要插入了!否则插入到当前rear指向的位置,然后再让rear++,但有可能rear++一下就越界了,所以要对他取队列实际长度的模~!如下图
//插入
void LQPush(LQ* p, LQDataType x)
{
assert(p);
if (IsFull(p))
{
perror("LQ is full");
exit(-1);
}
p->a[p->rear] = x;
p->rear++;
p->rear %= p->k + 1;
p->size++;
}删除
还是和前面的插入一样,得先判断是否为空。空了就不要删了!不是空的话就移动front但也要注意一中情况就是本身此时front就在最后,在++一下就越界了,所以得取模或特殊判断一下~!
//删除
void LQPop(LQ* p)
{
assert(p);
if (IsEmpty(p))
{
perror("LQ is empty");
exit(-1);
}
p->front++;
p->front %= p->k + 1;
p->size--;
}获取元素的个数
这里我定义了一个专门记录的元素size所以直接返回即可,如果没有专门定义size的话也可以用rear-front + 队列的实际长度 %队列的实际长度也可以~!!
//获取元素个数
int LQsize(LQ* p)
{
assert(p);
return p->size;
}获取队头数据
队头的数据相对简单,只要不为空把front的位置的元素返回即可~!
//获取队头的数据
LQDataType LQFront(LQ* p)
{
assert(p);
if (IsEmpty(p))
{
perror("LQ is empty");
exit(-1);
}
return p->a[p->front];
}获取队尾的数据
一般情况下,由于rear是当前元素的下一个所以-1直接返回即可,但如果rear此时就在0号下标的位置呢?-1就是负1越界了,所以这里得特殊判断, 当rear == 0时,就返回k的那个位置的元素(队列的实际长度是k+1)。当然还有大佬这样写的(rear + k+ 1) - 1 % (k+1),这种写法就是当你是第一个才有效,其他位置+个(k+1)%(k+1)一样的,简写就是:(rear+k )%(k+1)
//获取队尾的数据
LQDataType LQRear(LQ* p)
{
assert(p);
if (IsEmpty(p))
{
perror("LQ is empty");
exit(-1);
}
/*if (p->rear == 0)
return p->a[p->k];
else
return p->a[p->rear - 1];*/
return p->a[(p->rear + p->k) % (p->k + 1)];
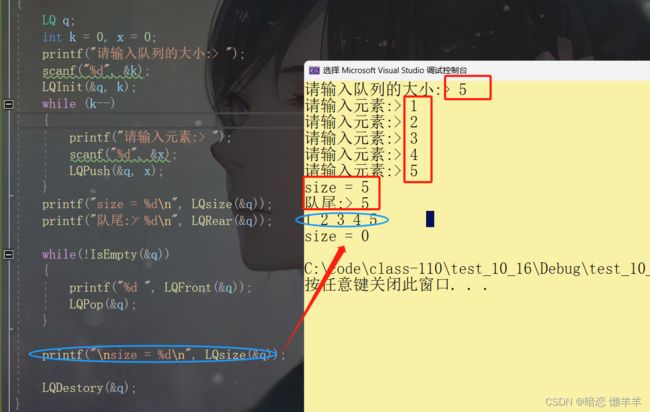
}OK,测试一把:
OK,没有什么问题。除了插入的元素有限以外这个结构还是很优秀的~!是当然可以自己输入的话可以预算一下也是可以用的~!
全部源码:
#define _CRT_SECURE_NO_WARNINGS 1
#include
#include
#include
#include
typedef int LQDataType;
typedef struct LQueNode
{
LQDataType* a;
int front;//队头
int rear;//队尾
int k;//队列的大小
int size;
}LQ;
//初始化
void LQInit(LQ* p, int k);
//销毁
void LQDestory(LQ* p);
//插入
void LQPush(LQ* p, LQDataType x);
//删除
void LQPop(LQ* p);
//是否为空
bool IsEmpty(LQ* p);
//是否为满
bool IsFull(LQ* p);
//获取元素个数
int LQsize(LQ* p);
//获取队头的数据
LQDataType LQFront(LQ* p);
//获取队尾的数据
LQDataType LQRear(LQ* p);
#include "Queue1.h"
初始化
//void LQInit(LQ* p,int k)
//{
// assert(p);
// p->front = p->rear = 0;//这里可以是-1,可以是0,我们这里采用后者
// p->size = 0;
//}
//销毁
//void LQDestory(LQ* p)
//{
// LQInit(p);
//}
//初始化
void LQInit(LQ* p, int k)
{
assert(p);
p->a = (LQDataType*)malloc(sizeof(LQDataType) * k + 1);
p->front = p->rear = 0;
p->k = k;
p->size = 0;
}
//销毁
void LQDestory(LQ* p)
{
assert(p);
free(p->a);
p->front = p->rear = 0;
p->k = p->size = 0;
}
//是否为空
bool IsEmpty(LQ* p)
{
assert(p);
return p->rear == p->front;
}
//是否为满
bool IsFull(LQ* p)
{
assert(p);
return (p->rear + 1) % (p->k + 1) == p->front;
}
//插入
void LQPush(LQ* p, LQDataType x)
{
assert(p);
if (IsFull(p))
{
perror("LQ is full");
exit(-1);
}
p->a[p->rear] = x;
p->rear++;
p->rear %= p->k + 1;
p->size++;
}
//删除
void LQPop(LQ* p)
{
assert(p);
if (IsEmpty(p))
{
perror("LQ is empty");
exit(-1);
}
p->front++;
p->front %= p->k + 1;
p->size--;
}
//获取元素个数
int LQsize(LQ* p)
{
assert(p);
return p->size;
}
//获取队头的数据
LQDataType LQFront(LQ* p)
{
assert(p);
if (IsEmpty(p))
{
perror("LQ is empty");
exit(-1);
}
return p->a[p->front];
}
//获取队尾的数据
LQDataType LQRear(LQ* p)
{
assert(p);
if (IsEmpty(p))
{
perror("LQ is empty");
exit(-1);
}
/*if (p->rear == 0)
return p->a[p->k];
else
return p->a[p->rear - 1];*/
return p->a[(p->rear + p->k) % (p->k + 1)];
}#include "Queue1.h"
void Test2()
{
LQ q;
int k = 0, x = 0;
printf("请输入队列的大小:> ");
scanf("%d", &k);
LQInit(&q, k);
while (k--)
{
printf("请输入元素:> ");
scanf("%d", &x);
LQPush(&q, x);
}
printf("size = %d\n", LQsize(&q));
printf("队尾:> %d\n", LQRear(&q));
while(!IsEmpty(&q))
{
printf("%d ", LQFront(&q));
LQPop(&q);
}
printf("\nsize = %d\n", LQsize(&q));
LQDestory(&q);
}
int main()
{
Test2();
return 0;
}OK,本期内容就介绍到这里,好兄弟我们下期再见~!