10.31日模拟赛总结
文章目录
- 考试时间及策略
- 考试结果
- 考试反思
- 题解
-
-
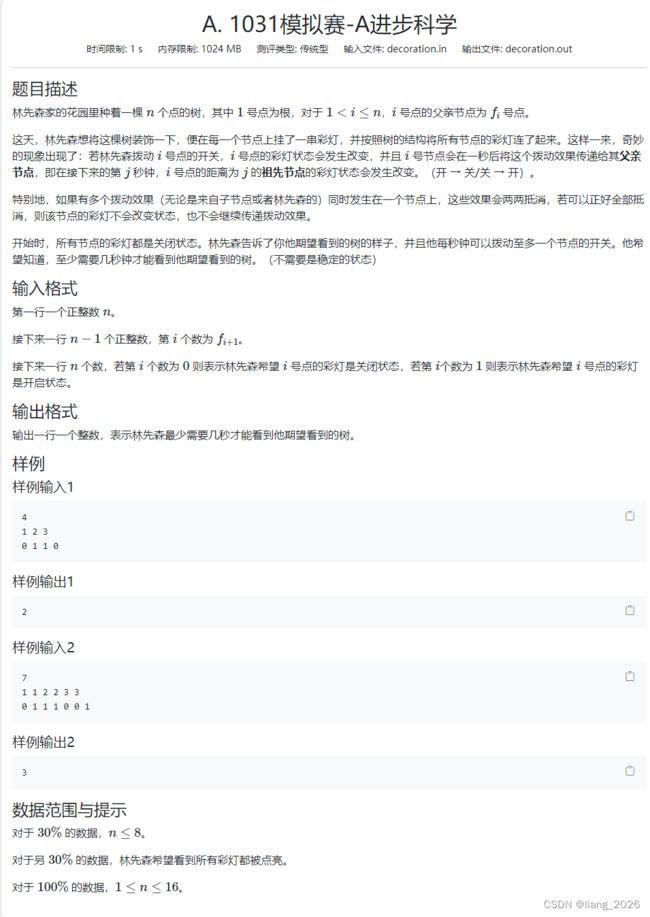
- A.进步科学
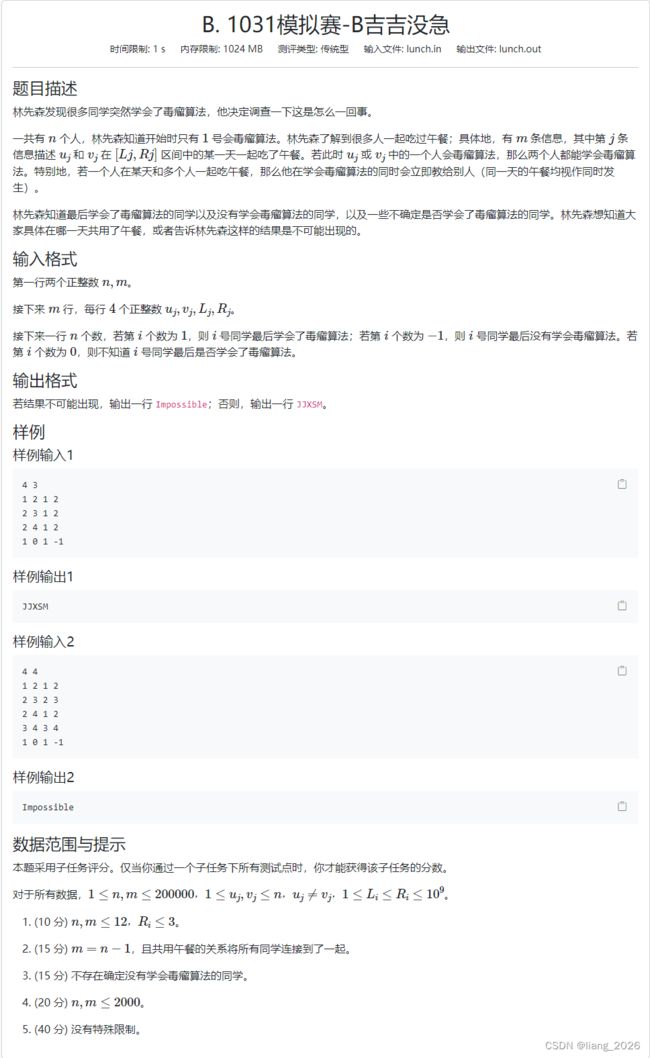
- B.吉吉没急
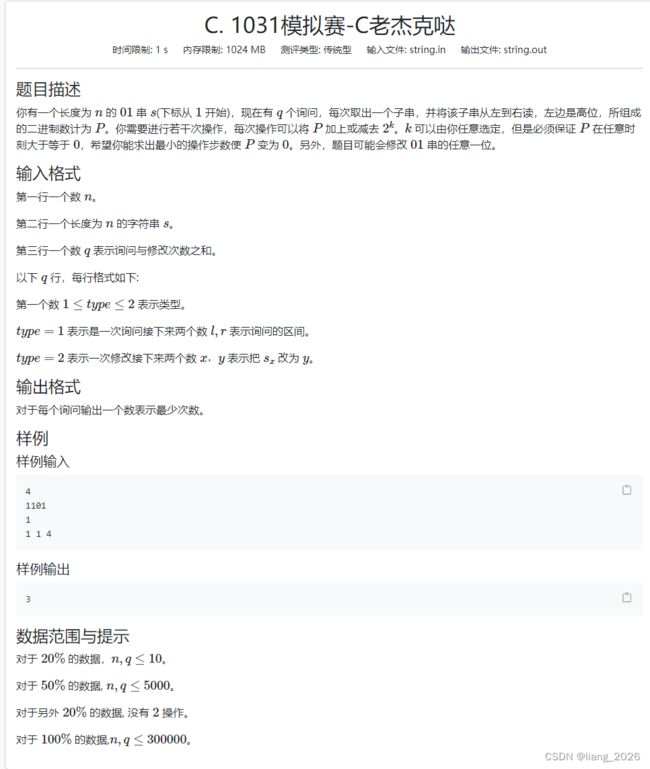
- C.老杰克哒
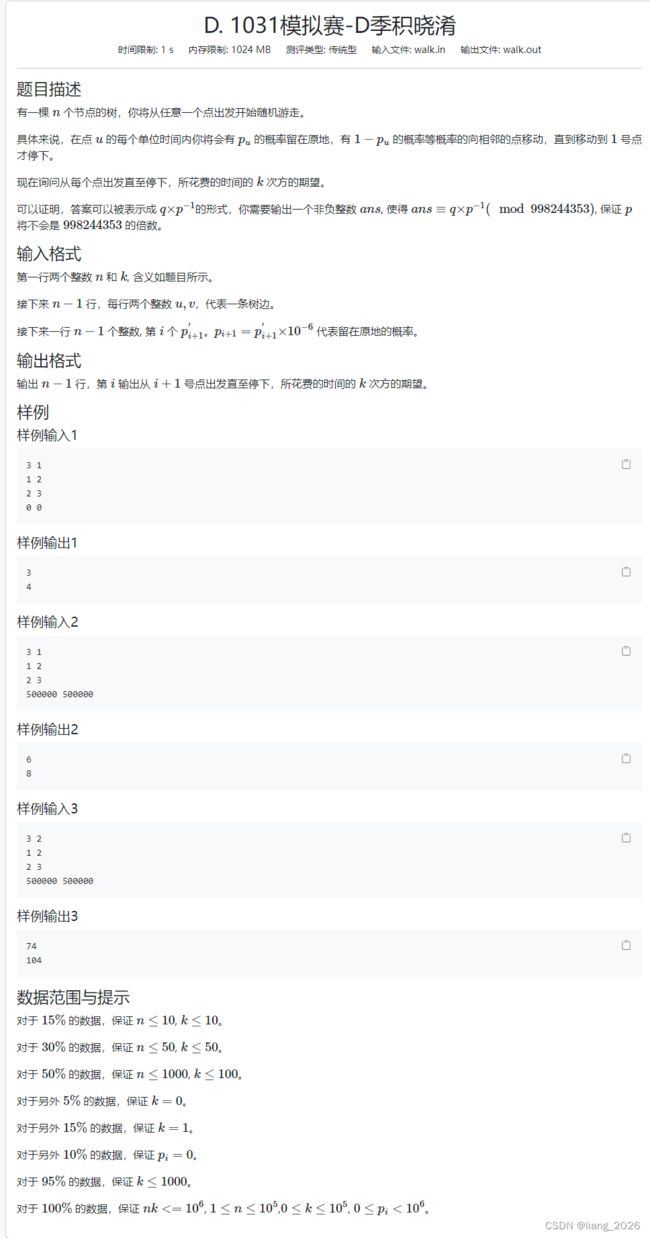
- D.季积晓淆
-
考试时间及策略
没啥好说的,因为好像都不会。所以全场感觉都在罚坐,很痛苦。
考试结果
30 + 0 + 50 + 5 = 85
考试反思
T1:T1是个神奇状压,感觉确实想不到。还是记住这个技巧吧。
T2:也是一道很难的题,会不了一点。
T3:只会 50pts 贪心的,没想出来暴力DP。如果能想出来暴力DP应该能想到正解吧。
T4:好像是FTT,会不了一点。
题解
A.进步科学
分析:
正常状压感觉没有什么阶段,我们设 d p i , m a s k dp_{i,mask} dpi,mask 表示第 i i i 秒所有树上的节点的状态为 m a s k mask mask 是否可行。
然后转移我们考虑若 d p i , m a s k = 1 dp_{i, mask} = 1 dpi,mask=1,那么我们让导致这个状态的操作整体后移1s,并且枚举第一秒操作哪个节点或者不操作节点。这样的好处是第 i + 1 i + 1 i+1 秒 可以直接继承第 i i i 秒的状态,不用再考虑前 i i i 秒的操作会不会在 第 i + 1 i + 1 i+1 秒产生影响。
我们设 j u m p i , j jump_{i, j} jumpi,j 表示如果扭动了第 i i i 个点,在扭动 j j j 秒后每个点的状态(最开始都是 0 0 0)。我们可以预处理出来 j u m p jump jump 数组,然后转移 就是如果第一秒扭动了点 u u u,那么 d p i , m a s k → d p i + 1 , m a s k ⊕ j u m p u , i dp_{i, mask} \to dp_{i+1, mask \oplus jump_{u, i} } dpi,mask→dpi+1,mask⊕jumpu,i。最后如果某一时刻询问的状态为 1 1 1 就直接输出就好了。可以想到最多 n n n 秒就一定能得到答案。
CODE:
#includeB.吉吉没急
分析:
很神奇的一道题。
我们首先把最后确定没学会算法的人当成一个限制。也就是说,我们考虑通过这些人来给其他人加一个限制。
具体来说,我们设 h i h_{i} hi 表示每个人 允许最早在什么时间学会算法。如果 x x x 最后没有学会,那么 h i = I N F h_i = INF hi=INF。我们跑一边 dijkstra ,设当前在堆头的点编号为 u u u,与它连边的点是 v v v,边的出现时间范围时 [ l , r ] [l,r] [l,r]。若 h u > r h_u > r hu>r,说明如果 v v v 这个人想要学会算法,最早得在 l + 1 l + 1 l+1 时刻,因为我们至少要拿出 1 s 1s 1s 使得这个时刻 v v v 还没学会算法, u u u 此时和他吃饭。而 l + 1 l + 1 l+1 相当与是这个限制的极限。我们将 h v h_v hv 赋值成 m a x ( h v , l + 1 ) max(h_v, l + 1) max(hv,l+1),如果更新了放入堆中。如果 h u ≤ r h_u \leq r hu≤r,也就意味着 h u h_u hu 允许在 r r r 之前学会算法,所以 h v h_v hv 什么时候学会都无所谓,我们只需要让边在某一个合适的时刻出现就好了。
跑完一边 dijkstra 后,我们检验一下 h 1 h_1 h1 是否大于 0 0 0。如果 h 1 h_1 h1 大于 0 0 0,那么一定无解,因为这意味着 1 1 1 号点不允许一开始就学会算法,与条件是冲突的。
否则,我们设 d i d_i di 表示每个点在满足 h i h_i hi 的限制下(也就是 d i d_{i} di 要大于等于 h i h_i hi)最早能够什么时候学会算法。因为每一个点越早学会算法,才越有可能教会其他最后确定学会的人。开始时 d 1 = 0 d_1 = 0 d1=0,其他的点设成 I N F INF INF,最后我们只需要检验所有确定学会的人 x x x 他的 d x d_x dx 是否等于 I N F INF INF 就好了。如果有一个等于,那么无解,否则有解。
相当于 h h h 数组用来检验能否满足让确定学不会的人能够学不会, d d d 数组用来保证确定学会的人可以学会。
CODE:
#includeC.老杰克哒
分析:
首先我们把区间内划分成若干 1 1 1 的连续段,那么对于一段,最多花费 2 2 2 的代价把它消除:我们可以现在后面加1,然后进位后在前面减1。并且一段至少需要花费1的代价。
基于上面的想法,我们可以考虑从后往前扫段,如果当前段长度大于1,那么就让它进位,否则就直接删掉。注意:进位后可能会与前面组成1段。所以这样做时肯定优的。贪心可以得到 50pts。
但是这样做没有什么优化的空间。我们考虑dp。
设 d p i , 0 / 1 dp_{i, 0/1} dpi,0/1 表示从开头到 i i i,字符串变成先一段连续的 0 0 0,然后一段连续的 0 / 1 0/1 0/1 的最小代价。考虑转移:
如果第 i i i 位是 0 0 0:
d p i , 0 ← d p i − 1 , 0 dp_{i, 0} \leftarrow dp_{i-1, 0} dpi,0←dpi−1,0, d p i , 0 ← d p i − 1 , 1 + 2 dp_{i,0} \leftarrow dp_{i-1, 1} + 2 dpi,0←dpi−1,1+2
d p i , 1 ← d p i − 1 , 0 + 1 dp_{i, 1} \leftarrow dp_{i - 1, 0} + 1 dpi,1←dpi−1,0+1, d p i , 1 ← d p i − 1 , 1 + 1 dp_{i, 1} \leftarrow dp_{i - 1, 1} + 1 dpi,1←dpi−1,1+1
解释一下上面的转移, d p i , 0 dp_{i, 0} dpi,0 可以由 d p i − 1 , 0 dp_{i - 1, 0} dpi−1,0 转移而来,代表什么也不操作, d p i , 0 dp_{i, 0} dpi,0 由 d p i − 1 , 1 + 2 dp_{i - 1, 1} + 2 dpi−1,1+2 转移过来,代表我们可以通过加1减1两次操作把前面的一段1给消除完,这样多的花费是2。 d p i , 1 dp_{i, 1} dpi,1 的转移同理。
如果第 i i i 位是 1 1 1:
d p i , 0 ← d p i − 1 , 0 + 1 dp_{i, 0} \leftarrow dp_{i - 1, 0} + 1 dpi,0←dpi−1,0+1, d p i , 0 ← d p i − 1 , 1 + 2 dp_{i, 0} \leftarrow dp_{i - 1, 1} + 2 dpi,0←dpi−1,1+2
d p i , 1 ← d p i − 1 , 0 dp_{i, 1} \leftarrow dp_{i - 1, 0} dpi,1←dpi−1,0, d p i , 1 ← d p i − 1 , 1 dp_{i, 1} \leftarrow dp_{i - 1, 1} dpi,1←dpi−1,1。
这转移和上面的是同理的。
那么对每一次询问,我们设左端点是 s t st st,实际上就是按照 S s t S_{st} Sst 的类型给 d p s t , 0 / 1 dp_{st, 0/1} dpst,0/1 一个初值,然后 O ( n ) O(n) O(n)转移。
我们发现转移是取 m i n min min,并且这个转移方式只跟当前为字符是 0 0 0 还是 1 1 1 有关。并且和矩阵乘法很想。我们对应 0 0 0, 1 1 1,直接构造两种矩阵,然后用线段树维护区间内矩阵的乘积,加速转移就好了。
CODE:
#includeD.季积晓淆
分析:
会不了一点 。