Grad-CAM++: Improved Visual Explanations for Deep Convolutional Networks 论文阅读笔记

Grad-CAM++: Improved Visual Explanations for Deep Convolutional Networks

会议：WACV
时间：2018年

本文针对Grad-CAM中出现的问题，例如当图像中存在多个目标或单个物体存在多个部分时，显著图无法将其全部标注、显著图无法完整地捕获整个对象的结构。面对上述问题，本文在CAM和Grad-CAM的基础上提出一个全新的可解释性算法Grad-CAM++，下面将对Grad-CAM++算法进行详细介绍。

1.Introduction

现有深度学习技术已在多个领域取得了实际应用。然而，基于深度学习方法与早期的人工智能系统有着根本的不同，在早期的人工智能系统中，主要的推理方法是逻辑和符号。这些早期的系统可以生成推理步骤的轨迹，然后成为解释的基础。另一方面，由于无法向人类用户解释智能系统的决策，当今智能系统的有效性受到了限制。这个问题对于安全、临床决策支持或自主导航等风险敏感型应用尤为重要。

因此，许多方法试图挖掘深度学习背后的原理。主要通过两种方式：第一种方式是解释该模型为什么将某图像预测为某个类别，另一种方式是通过改变网络输入，查看模型对应的结果变化，进而对模型做出分析。

近几年，CAM算法与Grad-CAM算法在网络可解释性上取得令人印象深刻的结果，这些方法可以解释 CNN 模型所做的预测，并提供所预测类别的细粒度细节。然而这些方法也有局限性–例如，在定位同一类别的多次出现时，其性能会下降，如下图所示。此外，对于只有单个目标的物体，Grad-CAM热力图常常**无法完整地捕获整个对象。**为解决上述问题，本文提出Grad-CAM++，一个用于解释CNN决策的更加通用的可视化工具，本文主要贡献如下：

• 在 CNN 的最终卷积特征图中，本文对特定空间位置的输出梯度进行像素加权。此方法可以衡量特征图中每个像素对 CNN 整体决策的重要性。
• 此前的可视化方法如CAM，Grad-CAM，Deconvnet，Guided back-propagation主要通过一些人工评估和辅助指标间接说明算法的决策有效性，而本文提出一个全新的衡量标准，以（客观地）评估所提出的解释是否忠实（faithfulness）于基础模型，即可视化是否与决策直接相关。
• 在人工测试、weakly supervised localization、师生模型、3D动作识别等领域进行大量实验，以证明算法有效性。

2.Related work

该部分主要对现有可解释性方法进行介绍，从Deconvnet、Guided backpropagation、CAM、Grad-CAM，到LIME、CENs等算法。由于本方法是在CAM和Grad-CAM上进行改进，为了方便下面的推导，这里把两篇文章的公式进行简短介绍。

CAM：

在带有GAP的卷积神经网络中，对于特定类别$c$的最终分类分数$Y^c$，可以写成最后一层卷积层特征图$A^k$全局池化后的线性组合：

$$Y^c=\sum _k{w}_k^c.\sum _i\sum _j{A}_{ij}^k（1）$$

在指定类别的显著图（saliency map）$L^c$中每个空间位置(i,j)可以表示成：

$$L_{ij}^c=\sum _k{w}_k^c.A_{ij}^k（2）$$

$L_{ij}^c$与特定空间位置（i，j）对特定类别$c$的重要性直接相关，因此可作为网络预测类别的直观解释。然而，CAM在没有GAP的网络层中需要对模型重新训练。

Grad-CAM

Grad-CAM则有效解决了上述问题。此方法将特定特征图$A^k$和类别$c$的权重$w_k^c$定义为：

$$w_k^c=\frac{1}{Z}\sum _i\sum _j\frac{\partial Y^c}{\partial A_{ij}^k}（3）$$

其中$Z$表示特征图中像素个数。根据上述公式，Grad-CAM 可以与任何深度CNN配合使用，在这种情况下，最终$Y^c$是特征图$A^k$的可微分函数，而无需任何重新训练或架构修改。但Grad-CAM的缺点在上述图中也已说明了，下面将介绍改进的算法Grad-CAM++。

3.Grad-CAM++：proposed methodology

3.1 Intuition

对于一个显著图$L^c$和一个二元目标分类任务，如果目标不存在则用输出0表示，1则表示存在，如下图所示。

其中$A^k$表示第k个特征图的可视化结果。根据[1,2]中描述，每个$A^k$由不同的抽象的视觉模式触发。在本例中，如果该模式被检测到，则用$A_{ij}^k=1$表示，如果没有被检测到则用0表示，而当该特征图的像素有助于识别目标时，导数$\frac{\partial y^c}{\partial A_{ij}^k}$将会比较大。为不失一般性，这里假设导数图为：

$$\begin{array}{rlrlr}\frac{\partial y^c}{\partial A_{ij}^k}& =1& & if& A_{ij}^k=1\\ & =0& & if& A_{ij}^k=0\end{array}（4）$$

将此公式（4）插入到公式（3）中，可以得到特征图对于给定输入图像$I$的权重，对于三个特征图权重分别为$w_1^c=\frac{15}{80}$，$w_2^c=\frac{4}{80}$，$w_3^c=\frac{2}{80}$。此时计算Grad-CAM的显著图$L_{grad-CAM}^c$可以发现，物体在原始图像中的占用空间（spatial footprint）对Grad-CAM的可视化十分重要。如果图中存在多个同类样本或一个物体的多个部分分布于不同得特征图，根据占据不同大小空间不同，占据空间大的物体得特征图权重会比较大，因此在最终显著图中效果明显，而占据空间较小得特征图最终会在显著图中消失。（上图计算出来之所以是1，0.26和0.13是以$w_1^c$为基准将其放大）

此问题可以通过对pixel-wise的梯度取加权平均解决。可以将公式3修改为以下公式：

$$w_k^c=\sum _i\sum _j{\alpha }_{ij}^{kc}.relu(\frac{\partial Y^c}{\partial A_{ij}^k})（5）$$

其中relu为激活函数，${\alpha }_{ij}^{kc}$表示类别c对特征图$A^k$在像素级梯度的权重系数。为解决上述问题，当${\alpha }_{ij}^{kc}$的定义为如下公式时：

$$\begin{array}{rlrl}{\alpha }_{ij}^{kc}& =\frac{1}{{\sum }_{l,m}\frac{\partial y^c}{\partial A_{lm}^k}}& if& \frac{\partial y^c}{\partial A_{ij}^k}=1\\ & =0& \mathrm{otherwise}& (6)\end{array}$$

所有特征图中的目标同样重要。假设对于$w_1^c$而言，原本$relu(\frac{\partial Y^c}{\partial A_{ij}^k})$的结果非1即0，但这里我们乘以一个$\frac{1}{15}$，这就使每个在原图中为1的部分的输出变成$\frac{1}{15}$。而第一个特征图中一共包含15个像素为1的位置，因此计算出的$w_k^c$就等于$\frac{1}{15}\times 15$，最终等于1，而其他几个特征图的结果经过同样方法计算均为1，这就使得不同特征图的权重是相同的。

这里我一开始一直有个疑问，如果​所有特征图​的权重都相同，那权重岂不是没有意义了？直接加权求和不就可以了？但是后来经过和师兄的讨论，这里权重相同的feature map指那些包含目标类别的feature map，其他不包含目标类别的特征图粗略地将其权重设置为0，当然这只是最理想的情况，这样合成的显著图会使目标类尽可能明显。（而且这里只是举个简单的例子说明对像素维度求梯度会如何解决上述问题，但在实际计算时很难达到这个结果）

在公式5中只考虑正梯度的想法类似于Deconvolution和Guided Backpropogation等工作。$w_k^c$表示特定激活图$A^k$的重要性，并且本文更倾向于用正梯度来表示增加输出神经元激活的视觉特征，而不是抑制输出神经元激活的视觉特征，关于该部分的讨论将在7.1节中介绍。

3.2 Methodology

这里推导出一种用于获得特定类别$c$的激活图$k$的梯度权重${\alpha }_{ij}^{kc}$的方法。首先使$Y^c$表示指定类别$c$的分数，将公式1与公式5集合，可以得到：

$$Y^c=\sum _k\{\sum _a\sum _b{\alpha }_{ab}^{kc}.relu(\frac{\partial Y^c}{\partial A_{ab}^k})\}[\sum _i\sum _j{A}_{ij}^k](7)$$

其中(i,j)和(a,b)是同一个激活图$A^k$的不同迭代，这里列出避免混淆。为不失一般性，这里在推导过程中暂时省略了ReLU激活函数，因为其仅仅是一个允许梯度反向传播的阈值。对上式两段同时对$A_{ij}^k$求偏导，可以得到：

$$\frac{\partial Y^c}{\partial A_{ij}^k}=\sum _a\sum _b{\alpha }_{ab}^{kc}.\frac{\partial Y^c}{\partial A_{ab}^k}+\sum _a\sum _b{A}_{ab}^k\{{\alpha }_{ij}^{kc}.\frac{{\partial }^2{Y}^c}{(\partial A_{ij}^k{)}^2}\}（8）$$

再对两端进一步求导，这里的2倍系数是由于公式8后半部分是两个部分相乘的，分别对前面和后面求导可以发现有一项可以与前面合并，最后就是两倍：

$$\frac{{\partial }^2{Y}^c}{(\partial A_{ij}^k{)}^2}=2.{\alpha }_{ij}^{kc}.\frac{{\partial }^2{Y}^c}{(\partial A_{ij}^k{)}^2}+\sum _a\sum _b{A}_{ab}^k\{{\alpha }_{ij}^{kc}.\frac{{\partial }^3{Y}^c}{(\partial A_{ij}^k{)}^3}\}（9）$$

重新对公式进行整理可得：

$${\alpha }_{ij}^{kc}=\frac{\frac{{\partial }^2{Y}^c}{(\partial A_{ij}^k{)}^2}}{2\frac{{\partial }^2{Y}^c}{(\partial A_{ij}^k{)}^2}+{\sum }_a{\sum }_b{A}_{ab}^k\{\frac{{\partial }^3{Y}^c}{(\partial A_{ij}^k{)}^3}\}}（10）$$

这里是所以采取这种计算方式是想通过求导让${\alpha }_{ij}^{kc}$单独列到等式的一侧，用其他公式表示。

再将公式10带入公式5，得到以下GradCAM++权重:

$$w_k^c=\sum _i\sum _j[\frac{\frac{{\partial }^2{Y}^c}{(\partial A_{ij}^k{)}^2}}{2\frac{{\partial }^2{Y}^c}{(\partial A_{ij}^k{)}^2}+{\sum }_a{\sum }_b{A}_{ab}^k\{\frac{{\partial }^3{Y}^c}{(\partial A_{ij}^k{)}^3}\}}].relu(\frac{\partial Y^c}{\partial A_{ij}^k})（11）$$

显然，与公式3相比，如果$\forall i,j,{\alpha }_{ij}^{kc}=\frac{1}{Z}$，Grad-CAM++可以化简为Grad-CAM，因此可以证明Grad-CAM++是Grad-CAM的广义表达。在下图中，本文对三种方法进行了比较：

3.3 Computation Analysis

本方法计算高阶导数的时间开销与Grad-CAM保持相同的阶数，因为只使用对角项(没有交叉高阶导数)。但是如果在神经网络的倒数第二层的输出分数上应用指数函数，并且最后一层的激活函数只是线性层的或者是ReLU（整流线性单元）函数，那么计算高阶导数就会变得非常简单。以下是对这段话的证明：

首先使$S^c$表示倒数第二层$c$类的分数

$$Y^c=exp(S^c)（12）$$

两边同时对$A_{ij}^k$求导

$$\frac{\partial Y^c}{\partial A_{ij}^k}=\exp (S^c)\frac{\partial S^c}{\partial A_{ij}^k}（13）$$

其中$\frac{\partial S^c}{\partial A_{ij}^k}$的值可以通过PyTorch或TensorFlow自动计算，之后再次求导：

$$\frac{{\partial }^2{Y}^c}{(\partial A_{ij}^k{)}^2}=\exp (S^c)\left[\right(\frac{\partial S^c}{(\partial A_{ij}^k)}{)}^2+\frac{{\partial }^2{S}^c}{(\partial A_{ij}^k{)}^2}]（14）$$

假设一个ReLU激活函数，$f(x)=max(x,0)$，其导数为：

$$\begin{array}{rlr}\frac{\partial f(x)}{\partial x}& =1& x>0\\ & =0& x\le 0\end{array}（15）$$

$$\frac{{\partial }^{2}f(x)}{\partial x^2}=0（16）$$

此外，即使激活函数是线性的（比如线性层）公式16也成立。之后将公式16带入公式14中，可得下式，这里之所以可以直接带入的原因是：本段开头已经说过网络的最后一层要为((20230808191136-wjm51ag “线性层或ReLU”))，这时候在反向传播的时候，在计算$S^c$对$A_{ij}^k$的导数之前，根据链式法则需要先计算最终预测结果对$S^c$的导数，如果通过一个线性层或ReLU，其二阶以上的导数恒为0，此时$S^c$对$A_{ij}^k$二阶以上的导数也为0，所以可以直接带入。

$$\frac{{\partial }^2{Y}^c}{(\partial A_{ij}^k{)}^2}=\exp (S^c)(\frac{\partial S^c}{\partial A_{ij}^k}{)}^2（17）$$

同样

$$\frac{{\partial }^3{Y}^c}{(\partial A_{ij}^k{)}^3}=\exp (S^c)(\frac{\partial S^c}{\partial A_{ij}^k}{)}^3（18）$$

将公式17和18插入至公式10中，可以得到：

$${\alpha }_{ij}^{kc}=\frac{(\frac{\partial S^c}{\partial A_{ij}^k}{)}^2}{2(\frac{\partial S^c}{\partial A_{ij}^k}{)}^2+{\sum }_a{\sum }_b{A}_{ab}^k(\frac{\partial S^c}{\partial A_{ij}^k}{)}^3}（19）$$

根据上式，这里只需要在计算图上进行一次反向传播，就可以求出${\alpha }_{ij}^{kc}$（因为公式中只需要对$A_{ij}^k$求一阶导，但在没有经过优化的公式需要求三阶）。这里由于指数函数比较简单，因此本文引入了指数函数。其他平滑函数（目的是能求高阶导），如 softmax 激活函数，也可以用相应的闭式表达式来计算权重。softmax 梯度权重的推导过程将在下文第 3.4 节中给出。

对于给定图像最终的显著图$L^c$，通过对不同激活图进行线性组合和ReLU构建：

$$L_{ij}^c=relu(\sum _k{w}_k^c.A_{ij}^k)（20）$$

与Grad-CAM相同，可以将最终的显著图使用上采样并与Guided Backpropagation进行点乘，得到Guided Grad-CAM++。

3.4 Gradient Weights for Softmax Function

与指数函数一样，softmax函数也是光滑的，通常用于在分类场景中获得最终的类概率。这种情况下，最后分类的分数$Y^c$定义为：

$$Y^c=\frac{exp(S^c)}{{\Sigma }_{k}exp(S^k)}（21）$$

其中$k$用于索引所有输出类，$S^k$表示导数第二层中输出类别的分数（这里目前还没从上面推导出来下面过）：

$$\frac{\partial Y^c}{\partial A_{ij}^k}=Y^c[\frac{\partial S^c}{\partial A_{ij}^k}-{\Sigma }_k{Y}^k\frac{\partial S^k}{\partial A_{ij}^k}]（22）$$

根据16公式，如果神经网络只有线性层或ReLU，$\frac{{\partial }^2{S}^c}{(\partial A_{ij}^k{)}^2}$也应等于0。

$$\begin{array}{rl}\frac{{\partial }^2{Y}^c}{(\partial A_{ij}^k{)}^2}& =\frac{\partial Y^c}{\partial A_{ij}^k}[\frac{\partial S^c}{\partial A_{ij}^k}-{\Sigma }_k{Y}^k\frac{\partial S^k}{\partial A_{ij}^k}]\\ & -Y^c\left({\Sigma }_k\frac{\partial Y^k}{\partial A_{ij}^k}\frac{\partial S^k}{\partial A_{ij}^k}\right)\end{array}（23）$$

$$\begin{array}{rl}& \frac{{\partial }^3{Y}^c}{(\partial A_{ij}^k{)}^3}=\frac{{\partial }^2{Y}^c}{(\partial A_{ij}^k{)}^2}\left[\frac{\partial S^c}{\partial A_{ij}^k}-{\Sigma }_k{Y}^k\frac{\partial S^k}{\partial A_{ij}^k}\right]\\ & -2\frac{\partial Y^c}{\partial A_{ij}^k}\left({\Sigma }_k\frac{\partial Y^k}{\partial A_{ij}^k}\frac{\partial S^k}{\partial A_{ij}^k}\right)-Y^c\left({\Sigma }_k\frac{{\partial }^2{Y}^k}{(\partial A_{ij}^k{)}^2}\frac{\partial S^k}{\partial A_{ij}^k}\right)\end{array}（24）$$

将公式23和24插入公式10，得到最终的权重。需要注意的是，虽然软最大函数的梯度权重计算比指数函数的梯度权重计算更复杂，但仍然可以通过计算图中的一次后向传递来计算$\frac{\partial S^k}{\partial A_{ij}^k}$。

4.Experiments and results

这里使用VGG-16模型，进行大量主观和客观的实验，同时在补充实验部分还使用AlexNet和ResNet-50结构进行大量实验。

4.1 Objective Evaluation for Object Recognition

这里先证明Grad-CAM++在目标检测任务上的faithfulness。对于任意一张图片，其相应的解释图$E^c$是通过类显著图（上采样后的）和输入图像逐点相乘得到的，公式定义如下：

$$E^c=L^c\circ I$$

其中$\circ$表示Hadamard product（哈马达积，也成为基本积，点积），$I$为输入图像，$c$为模型预测的类别，$L^c$为公式20得到的类显著图。这里使用了三个评价指标进行衡量：Average drop%、% increase in confidence、Win %，下面将分别对这三个指标进行详细介绍。

（i）Average Drop %：

一个好的类解释图应该突出与决策最相关的区域。根据上述想法，这里提供了一个算法通过计算将完整图像作为输入和仅将模型学习的解释图作为输入，分别计算网络对该类的置信度变化，数学表达式如下：

$$(\sum _{i=1}^N\frac{max(0,Y_i^c-O_i^c)}{Y_i^c})100$$

其中$Y_i^c$表示原始输入图像第$c$个类别的第$i$张图像置信度，$O_i^c$表示解释图作为输入的置信度，该指标越小表明两个置信度差距越小，表明结果越好。为了防止出现$O_i^c>Y_i^c$的情况，这里取了一个max函数。结果如下表所示：

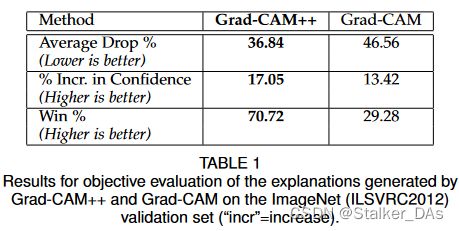
可以看到虽然两种方法均存在置信度下降（可能是由于移除了上下文信息导致的），但Grad-CAM++的效果更好，说明其解释图保留了更多相关正确的信息。

（ii）% Increase in Confidence：

此评价指标是对上面评价指标的一个补充，本文认为在一些情况下，将解释图作为输入反而会增加预测的可信度（特别是在上下文中存在干扰信息的时候）。该指标主要衡量解释图对预测置信度的提升值大小，公式如下：

$$(\sum _{i=1}^N\frac{{\text{1}}_{Y_i^c}<O_i^c}{N})100$$

其中${\text{1}}_x$为指示函数（indicator function）。

（iii）Win %：

该指标作为上述指标的进一步补充，衡量在给定一组图像中，生成的解释图的模型置信度下降的次数，并对Grad-CAM++和Grad-CAM进行了百分比计算。

在RASCAL VOC 2007上的实验结果如下：

4.2 Evaluating Human Trust

该实验主要衡量人类对本模型的可解释性或信任度。本实验在ImageNet数据集上选取5个类，共包含250张图像。让13个对该领域一无所知的测试人员对Grad-CAM和Grad-CAM++解释后的图像对进行评价，解释图片如下图所示：

对于每个图像的结果，本文将其进行归一化，使得每个图像的总分（最大）可能为1.0。计算方式如下：本文为每幅图像收集了 13 个回答。例如，在 13 个回答中，如果有 5 个选择了由 Grad-CAM++ 生成的解释图，4 个选择了由 Grad-CAM 生成的解释图，4 个选择了 "相同 "选项，则 Grad-CAM++ 和 Grad-CAM 的得分分别为 0.38 和 0.31（其余为 “相同”）。然后将这些标准化分数相加，可达到的总分最高为250分。最终Grad-CAM++取得分数109.69，Grad-CAM取得56.08，剩余84.23被认为是效果相同。此实验可以证明Grad-CAM++中提出的改进有助于人类可解释的图像定位，从而提高了对做出决策的模型的信任。

4.3 Harnessing Explanations for Object Localization

本实验验证Grad-CAM++构成的解释图在目标定位上的作用。对于给定图像和指定类别$c$，通过公式25构建相应的解释图$E^c(\delta )$，该解释图是显著图$L^c$通过min-max normalizaed将数据归一到0，1之间，并通过一个阈值$\delta$将阈值以上的像素设置为1。这里定义了一个IoU度量$Lo{c}_I^C(\delta )$，公式如下：

$$Lo{c}_I^c(\delta )=\frac{Area(\text{internal pixel}s)}{Area(\text{bounding bo}x)+Area(\text{external pixel}s)}$$

其中$Area(boundingbox)$表示在给定图像$I$中，box的区域大小。$Area(internalpixels)$表示在解释图中非零的区域且在box内的像素数量。$Area(externalpixels)$表示在解释图中非零的区域且不在box内像素的数量。更高的$Lo{c}_I^C(\delta )$表示可解释图具有更好的定位能力，可视化效果如下图所示：

在不同阈值下结果如下表所示：

5.Learning from explanations：knowledge distillation

该部分主要涉及知识蒸馏，由于没有接触过相关知识，这里先暂时略过。

6.Explanations for Image Captioning and 3D Action recognition

此部分通过两个任务：图像描述（Image Captioning）和3D动作识别（3D Action Recognition）证明可解释性的有效性。

6.1 Image Captioning

本实验主要对图像描述的模型进行解释，可视化模型更关注的区域，本实验随机选取4张图像并进行可视化，结果如下所示：

可以看到例如：再第一张图像中，Grad-CAM++在标题“一个小女孩和一棵小植物”中突出显示了女孩和植物，而GradCAM只突出显示了女孩。而在第二个例子中，尽管预测标题是错误的，通过 GradCAM++ 的可视化，我们可以了解到网络关注的焦点–有色玻璃（被网络预测为支柱）和人。而相比之下，GradCAM的可视化是不完整的，在图像中男人的空间位置没有产生热量。而在附录中还进行了其他相关实验，比如使用5种不同的标题，分别显示其关注区域。

6.2 3D Action Recognition

7. Discussion

7.1 Why only Positive Gradients in Grad-CAM++？

这里讨论了在3.2节中公式5中，本文强调需要使用一个ReLU对负梯度进行过滤，本节将通过放松对梯度的约束来检验这个假设的正确性。这里使用公式如下所示：

$$w_k^c=\sum _i\sum _j{\alpha }_{ij}^{kc}.\frac{\partial Y^c}{\partial A_{ij}^k}$$

${\alpha }_{ij}^{kc}$的计算方式与公式10相同，除了在计算负梯度时${\alpha }_{ij}^{kc}\ne 0$。这里考虑负梯度的模型用Grad-CAM++^⊥表示，结果如下所示：

但这里我看了下在VOC 2007上Grad-CAM++的结果，第二个指标只有18.96，同样没有高于Grad-CAM，也就是在Grad-CAM++下，使用去掉背景的特征图反而会降低网络的预测置信度，这点需要考虑下为什么？是否有可以改进的空间。

7.2 Does Grad-CAM++ do well because of larger maps？

人们可能会质疑 Grad-CAM++比Grad-CAM效果更好，是否是因为扩大了每幅图像中的解释区域？一般来说，如果给定图像$I$和类别 $c$输入模型的解释图区域面积越大，我们更期望分类得分的下降幅度会较小，因此这里绘制了一条ROC曲线以度量被遮挡面积和分类的置信度（$\frac{O_I^c\ast 100}{Y_I^c}$，其中$O_I^c$表示遮挡后图像的分数，$Y_I^c$表示原图分数），结果如下图所示：

参考文献

[1]. M. D. Zeiler and R. Fergus, “Visualizing and understanding convolutional networks,” in European conference on computer vision. Springer, 2014, pp. 818–833.

[2]. B. Zhou, A. Khosla, A. Lapedriza, A. Oliva, and A. Torralba, “Object detectors emerge in deep scene cnns,” arXiv preprint arXiv:1412.6856, 2014.