【C++】无重复数字全排列(三种方法)和有重复数字全排列

---

一、无重复数字排列

1.1 题目描述

 把 $1\sim n$ 这 $n$ 个整数排成一行后随机打乱顺序，输出所有可能的次序。

输入格式：
一个整数 $n$。$1\le n\le 9$。
输出格式：
按照从小到大的顺序输出所有方案，每行 $1$ 个。
首先，同一行相邻两个数用一个空格隔开。
其次，对于两个不同的行，对应下标的数一一比较，字典序较小的排在前面。

1.2 用dfs方法

1.2.1 思路分析

 1. 这个问题其实就是求无重复元素的全排列，经典的 $dfs$ 题。$dfs$ 最重要的是搜索顺序，用什么顺序遍历所有方案。对于全排列问题，以 $n=3$ 为例，可以这样进行搜索：

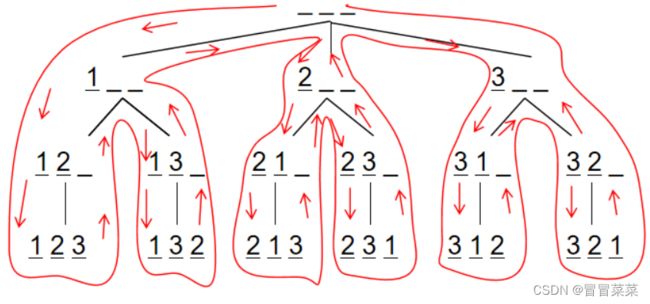
 假设有 3 个空位，从前往后填数字，每次填一个位置，填的数字不能和前面一样。

 最开始的时候，三个空位都是空的：__ __ __

 首先填写第一个空位，第一个空位可以填 1，填写后为：1 __ __

 填好第一个空位，填第二个空位，第二个空位可以填 2，填写后为：1 2 __

 填好第二个空位，填第三个空位，第三个空位可以填 3，填写后为： 1 2 3

 这时候，空位填完，无法继续填数，所以这是一种方案，输出。

 然后往后退一步，退到了状态：1 2 __ 。剩余第三个空位没有填数。第三个空位上除了填过的 3 ，没有其他数字可以填。

 因此再往后退一步，退到了状态：1 __ __。第二个空位上除了填过的 2，还可以填 3。第二个空位上填写 3，填写后为：1 3 __

 填好第二个空位，填第三个空位，第三个空位可以填 2，填写后为： 1 3 2

 这时候，空位填完，无法继续填数，所以这是一种方案，输出。

 然后往后退一步，退到了状态：1 3 __ 。剩余第三个空位没有填数。第三个空位上除了填过的 2，没有其他数字可以填。

 因此再往后退一步，退到了状态：1 __ __。第二个空位上除了填过的 2，3，没有其他数字可以填。

 因此再往后退一步，退到了状态：__ __ __。第一个空位上除了填过的 1，还可以填 2。第一个空位上填写 2，填写后为：2 __ __

 填好第一个空位，填第二个空位，第二个空位可以填 1，填写后为：2 1 __

 填好第二个空位，填第三个空位，第三个空位可以填 3，填写后为：2 1 3

 这时候，空位填完，无法继续填数，所以这是一种方案，输出。

 然后往后退一步，退到了状态：2 1 __ 。剩余第三个空位没有填数。第三个空位上除了填过的 3，没有其他数字可以填。

 因此再往后退一步，退到了状态：2 __ __。第二个空位上除了填过的 1，还可以填 3。第二个空位上填写 3，填写后为：2 3 __

 填好第二个空位，填第三个空位，第三个空位可以填 1，填写后为：2 3 1

 这时候，空位填完，无法继续填数，所以这是一种方案，输出。

 然后往后退一步，退到了状态：2 3 __ 。剩余第三个空位没有填数。第三个空位上除了填过的 1，没有其他数字可以填。

 因此再往后退一步，退到了状态：2 __ __。第二个空位上除了填过的 1，3，没有其他数字可以填。

 因此再往后退一步，退到了状态：__ __ __。第一个空位上除了填过的 1，2，还可以填 3。第一个空位上填写 3，填写后为：3 __ __

 填好第一个空位，填第二个空位，第二个空位可以填 1，填写后为：3 1 __

 填好第二个空位，填第三个空位，第三个空位可以填 2，填写后为：3 1 2

 这时候，空位填完，无法继续填数，所以这是一种方案，输出。

 然后往后退一步，退到了状态：3 1 __ 。剩余第三个空位没有填数。第三个空位上除了填过的 2，没有其他数字可以填。

 因此再往后退一步，退到了状态：3 __ __。第二个空位上除了填过的 1，还可以填 2。第二个空位上填写 2，填写后为：3 2 __

 填好第二个空位，填第三个空位，第三个空位可以填 1，填写后为：3 2 1

 这时候，空位填完，无法继续填数，所以这是一种方案，输出。

 然后往后退一步，退到了状态：3 2 __ 。剩余第三个空位没有填数。第三个空位上除了填过的 1，2，没有其他数字可以填。

 因此再往后退一步，退到了状态：3 __ __。第二个空位上除了填过的 1，2，没有其他数字可以填。

 因此再往后退一步，退到了状态：__ __ __。第一个空位上除了填过的 1，2，3，没有其他数字可以填。

 此时深度优先搜索结束，输出了所有的方案。

输入样例：
3
输出样例：
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1

时间复杂度为 $O(n\ast n!)$。

1.2.2 代码编写

 用 $path$ 数组保存排列，当排列的长度为 $n$ 时，是一种方案，输出。
 用 $state$ 数组表示数字是否用过。当 $state[i]$ 为 $1$ 时：$i$ 已经被用过，$state[i]$ 为 $0$ 时，$i$ 没有被用过。
 $dfs(i)$ 表示的含义是：在 $path[i]$ 处填写数字，然后递归的在下一个位置填写数字。
 回溯：第 $i$ 个位置填写某个数字的所有情况都遍历后， 第 $i$ 个位置填写下一个数字。

#include
using namespace std;
const int N = 10;
int path[N];  //保存序列
int state[N]; //数字是否被用过
int n;
void dfs(int u)
{
    if(u > n)//数字填完了，输出
    {
        for(int i = 1; i <= n; i++) //输出方案
            cout << path[i] << " ";
        cout << endl;
    }

    for(int i = 1; i <= n; i++) //空位上可以选择的数字为:1 ~ n
    {
        if(!state[i])    //如果数字 i 没有被用过
        {
            path[u] = i; //放入空位
            state[i] = 1;//数字被用，修改状态
            dfs(u + 1);  //填下一个位
            state[i] = 0;//回溯，取出 i
        }
    }
}

int main()
{

    cin >> n;
    dfs(1);
    return 0;
}

1.3 用交换法

 交换法思想就是定下一个前缀，然后将后面的数全排列。

#include
using namespace std;
int n;
//int cnt = 0; cnt用来计数的 
void Permutation(int *s,int p) //从数组s的第p个位置开始全排列
{
    if(p==n)
    {
        for(int i=0;i<n;i++) 
        {
        	cout<<s[i];
	    }
	    cout<<endl;
        //可计数有多少种排序cnt++;
    }
    for(int i=p;i<n;i++)
    {
        swap(s[i],s[p]);  //每个字符都有成为当前起始字符的机会
        Permutation(s,p+1);
        swap(s[i],s[p]);  //返回初始状态，才能保证后面的交换是正确的，回溯
    }
}
int main()
{
	cin>>n;
    int s[n];
    for(int i=0;i<n;i++) 
    {
    	s[i]=i+1;
	}
    Permutation(s,0);
    //cout <
    return 0;
}

1.4 STL秒解

1.4.1 所用函数

 1. next_permutation的功能是生成给定序列的下一个字典序排列。这个函数在C++ STL中，对于解决排列组合问题和迭代遍历所有可能排列时非常有用。
 2. prev_permutation的功能是生成给定序列的前一个字典序排列。这个函数在C++ STL中，可以用于迭代遍历所有可能的排列，与next_permutation相反，它是从大到小的顺序生成排列。

1.4.2 代码编写

#include 
#include //头文件
using namespace std;
int main()
{
	int n;
	cin>>n;
    int s[n];
    for(int i=0;i<n;i++) 
    {
    	s[i]=i+1;
	}
    //int cnt = 0;
    do
    {
        for(int i=0;i<n;i++) 
        {
        	cout<<s[i];
	    }
	    cout<<endl;
    }while(next_permutation(s,s+n));//起始位置，左闭右开
    
    //cout<<"总共有："<
    return 0;
}

二、有重复数字排列

2.1 思路分析

 1. 看到这个题目首先能想到的一点就是：(1) 我们要求元素的所有全排列。(2) 我们要对求出的全排列去重。

 2. 求全排列用交换递归；去重我们可以设计一个函数来判断这个元素是否前面已经用到过了。

2.2 代码编写

#include 
using namespace std;
int count=0;
void swap(char &a,char &b)
{
	char temp;
	temp=a;
	a=b;
	b=temp;
}
int finish(char list[],int k,int i)
{   //第i个元素是否在前面元素[k...i-1]中出现过
	if(i>k)
	{
		for(int j=k;j<i;j++)
			if(list[j]==list[i])
				return 0;
	}
	return 1;
}
void perm(char list[],int k,int m)
{
	if(k==m)    //当只剩下一个元素时则输出
	{
		count++;
		for(int i=0;i<=m;i++)
			cout<<list[i];
		cout<<endl;
	}
	for(int i=k;i<=m;i++)  //还有多个元素待排列，递归产生排列
	{
		if(finish(list,k,i))
		{
			swap(list[k],list[i]);
			perm(list,k+1,m);
			swap(list[k],list[i]);
		}
	}
}
int main()
{
	int i,n;
	cout<<"请输入元素个数: "<<endl;
	cin>>n;
	cout<<"请输入待排列的元素: "<<endl;
	//getchar();
	char *a=new char[n];
 
	for(i=0;i<n;i++)
		cin>>a[i];
	cout<<"所有不同排列为: "<<endl;
	perm(a,0,n-1);
	cout<<"排列总数为： "<<count<<endl;
	return 0;
}