leetcode:239. 滑动窗口最大值
题目来源
- leetcode:239. 滑动窗口最大值
题目描述
class Solution {
public:
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
}
};
题目解析
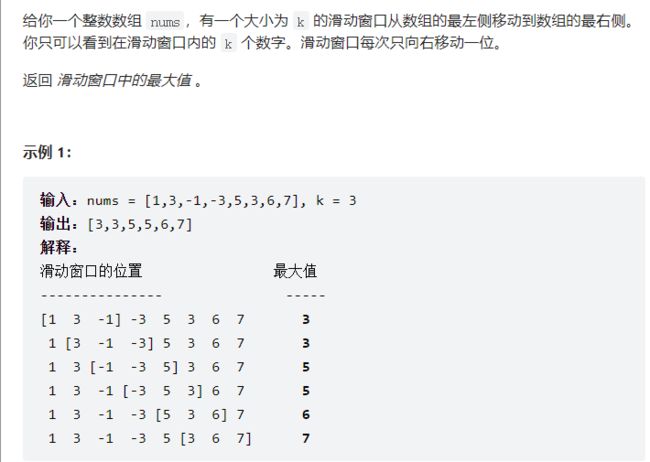
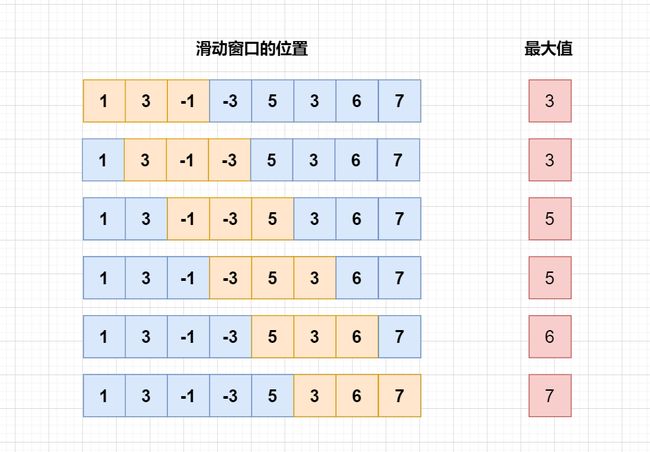
题目相当于维护了一个大小为3的滑动窗口,并输出每个滑动窗口内的最大值
那么什么是滑动窗口呢?
举个例子,我们从数组中第一个元素开始遍历,由于窗口的大小是 3 3 3,因此当遍历到第三个元素时候窗口就形成了
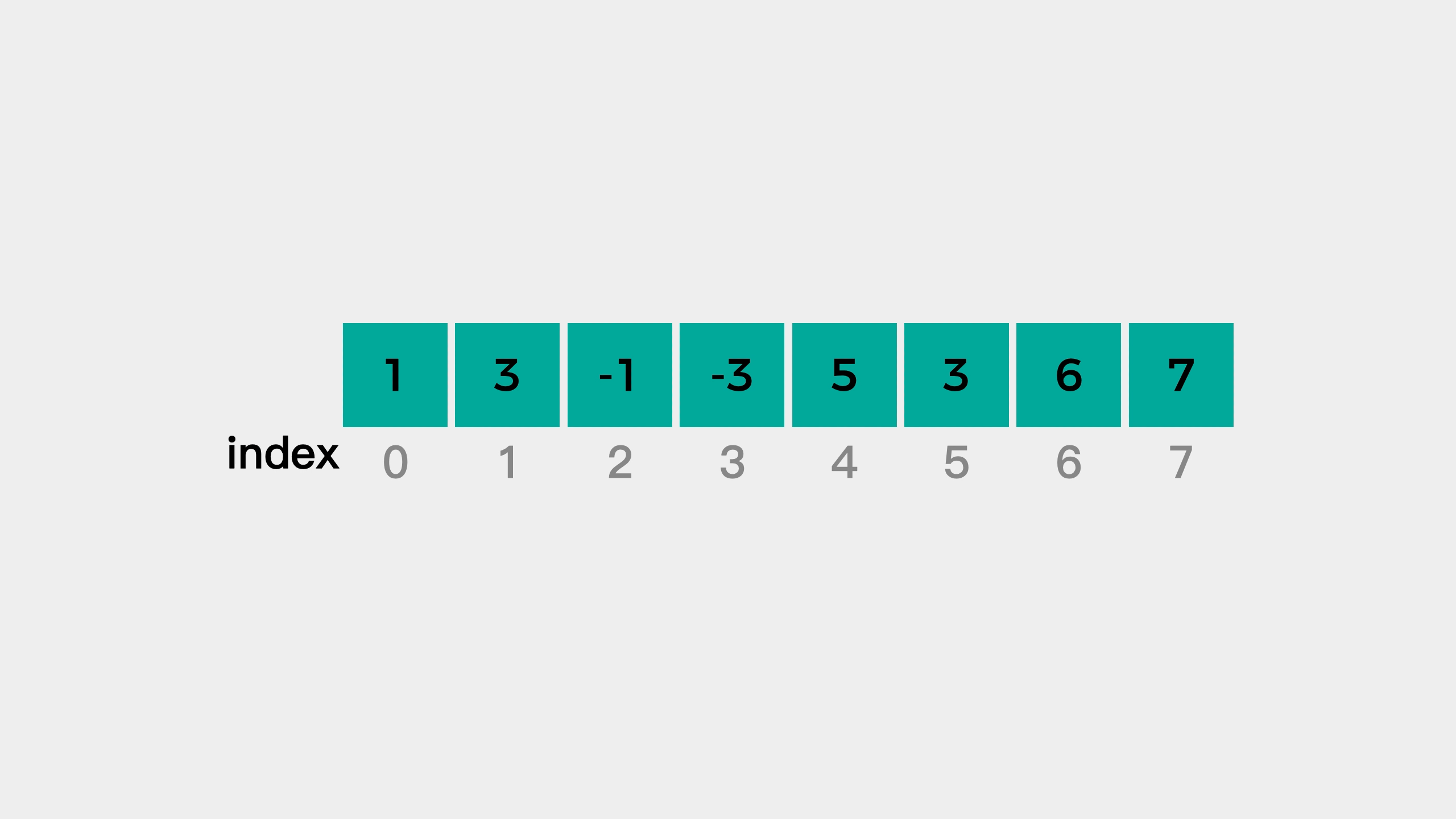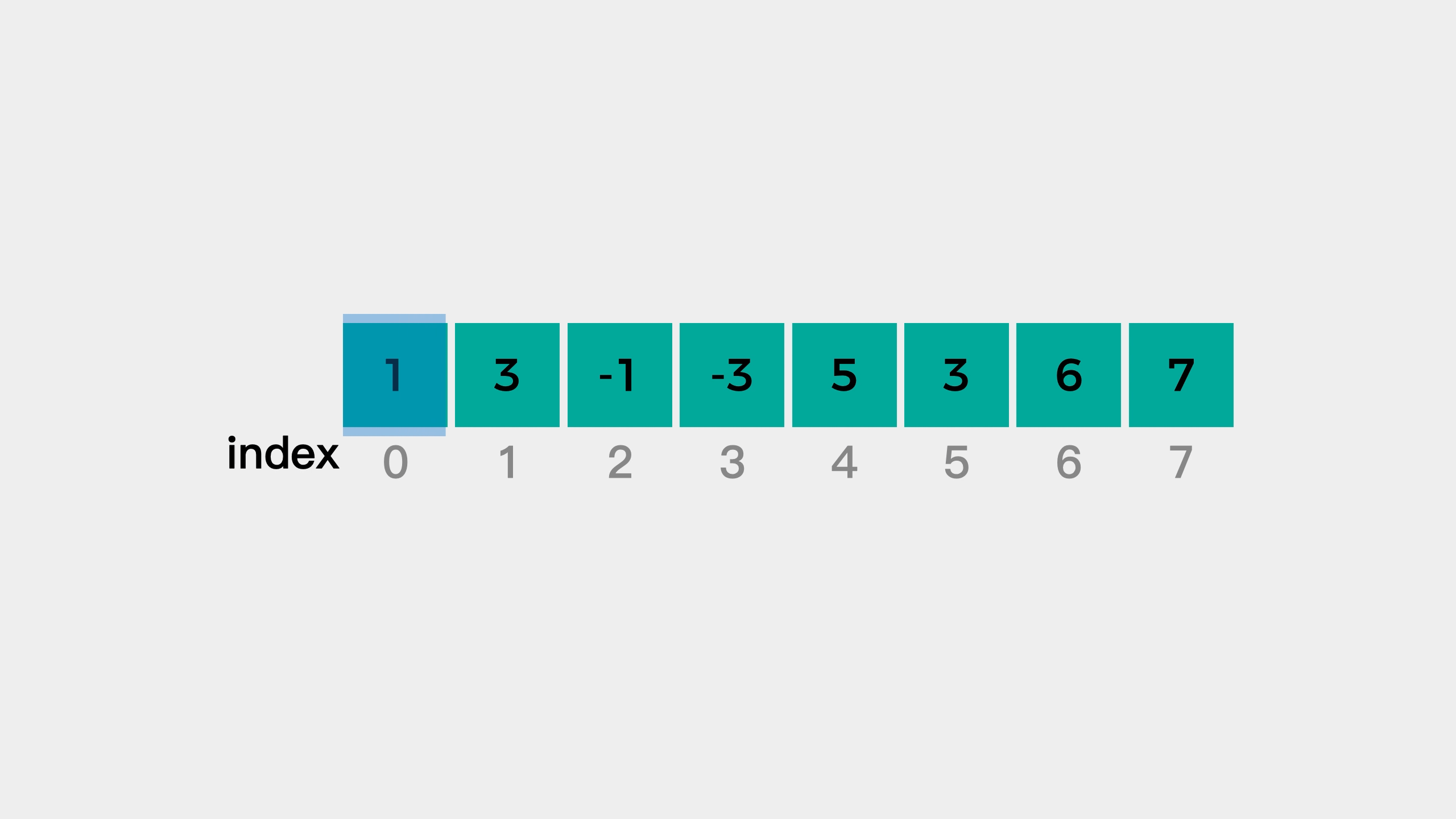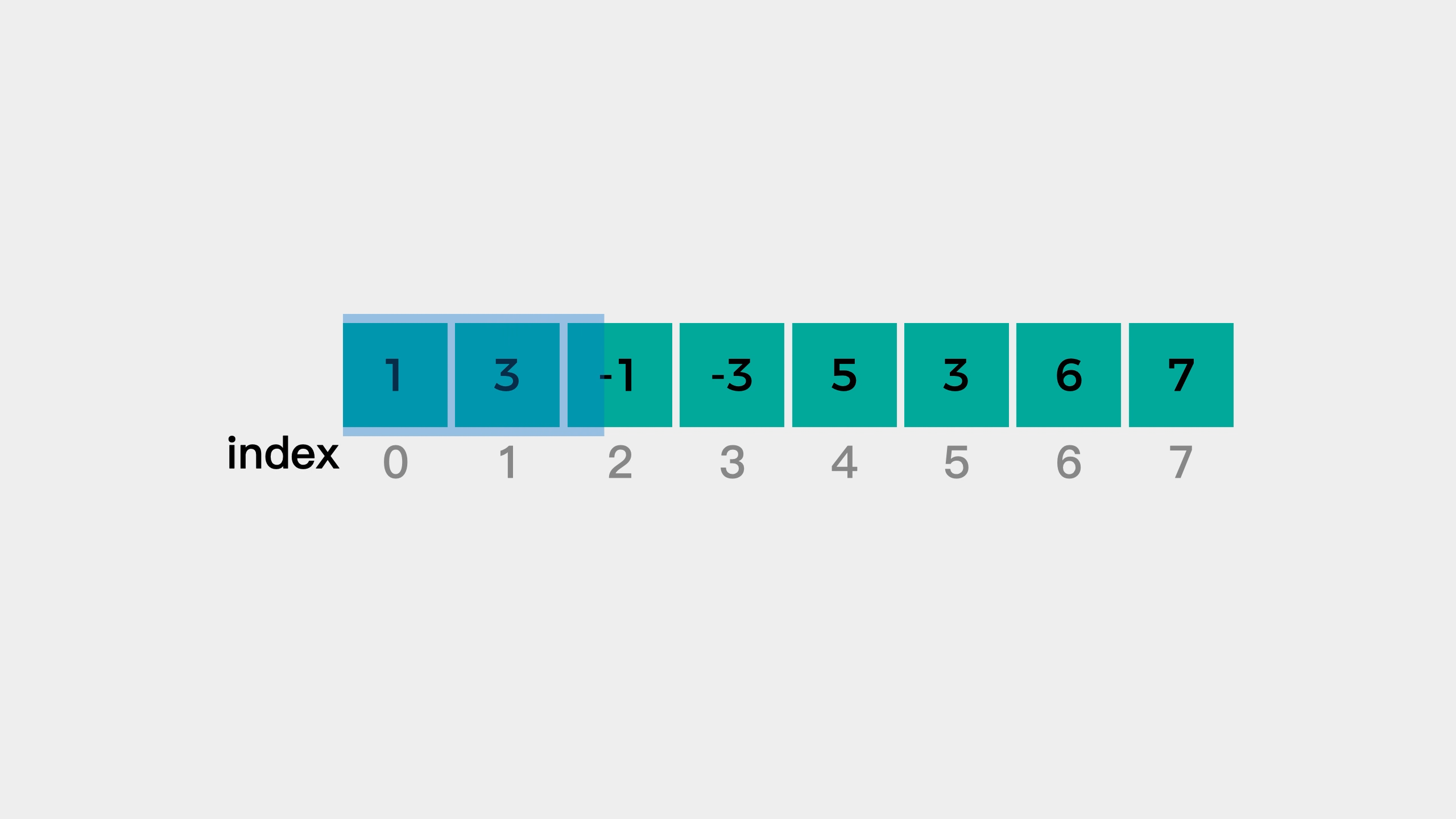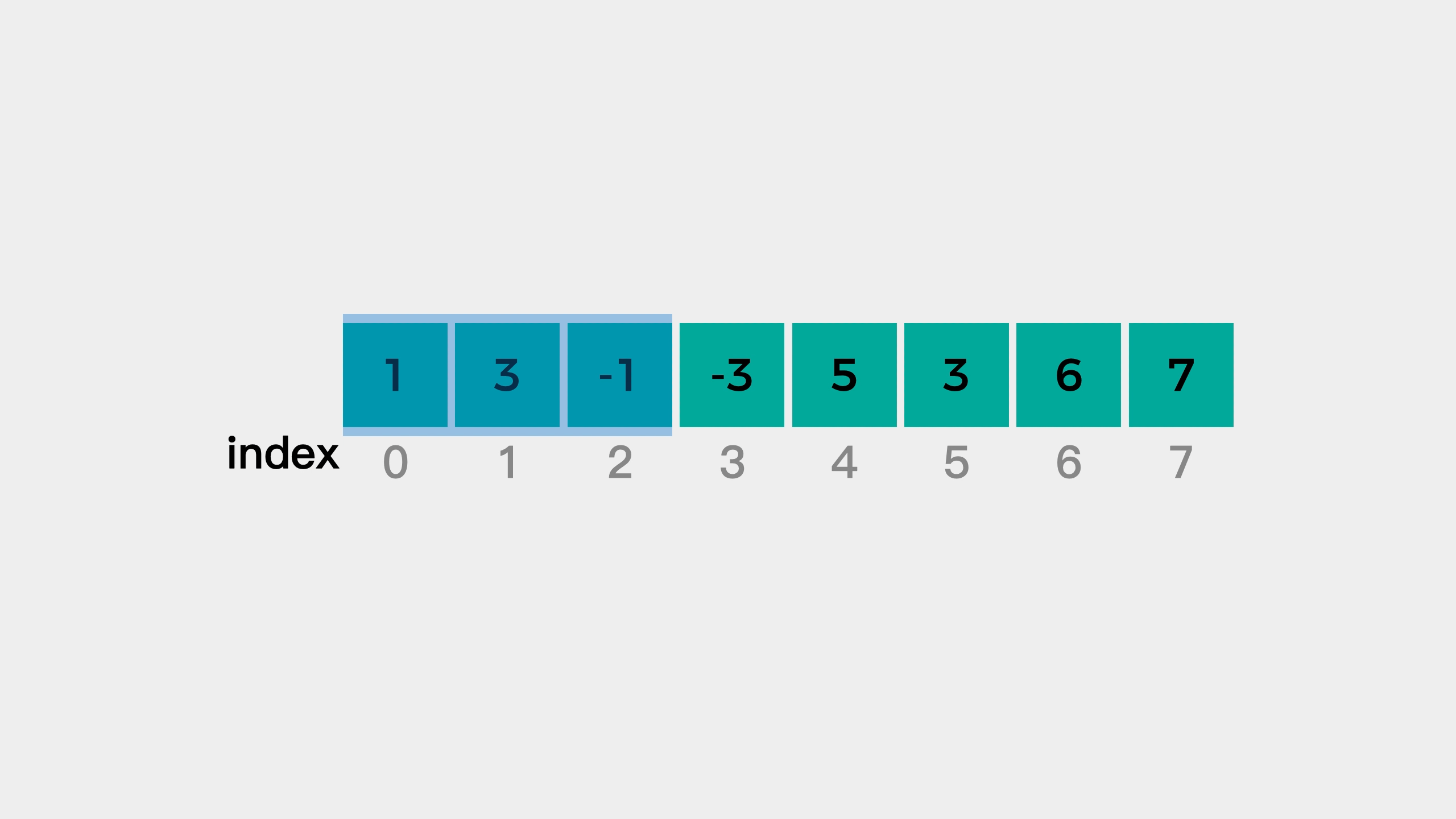
之后,继续遍历元素,为了保持窗口的大小为3,左侧元素就需要从窗口中剔除。这样就使得窗口一直向右移动,直到考察到最后一个元素结束,这就是所谓的滑动窗口。
怎么实现呢?我们分别维护两个变量L,R为表示一个窗口。那么,应该怎么滑动呢?令N = arr.size()
- 刚开始时,L和R均指向-1,表示尚未开始滑动(L和R都是索引值而不是元素值)
- 什么时候L滑动呢,什么时候R滑动呢?什么时候停止呢?最大能够给滑动到哪里呢?
- 谁先滑动?是L先滑动还是R先滑动,还是同时滑动
- 同时滑动肯定是不行的,因为这样窗口大小就一直为0了
- 因为窗口不能是负值,所以R必须保证永远大于等于L,R应该先滑动
- L和R滑动有什么意义?
- 每次R往前移动一个位置,就表示有一个元素从右侧进入了窗口,窗口大小加一
- 每次L往前移动一个位置,就表示有一个元素从左侧移出了窗口,窗口大小减一
- 窗口大小是什么东西?
- 窗口大小为: R - L(窗口有多大,就存放了多少个元素)
- 当L == R时,表示窗口大小为0,也就是窗口内没有一个元素
- 什么时候停止?
- 因为窗口框住的是元素,所以L和R最多只能移动到N-1的位置
- R指向的位置表示窗口最右边的那个元素
- L指向的位置表示这个位置的元素过期了
- 因为我们维护一个大小为K的窗口,所以每次元素入窗口(R++),我们要看看一次当前窗口大小,以及有没有元素需要过期
- 当 R - L < L时,R继续往后移动
- 当 R - L == K时,窗口形成了
- 当 R - L > K时,L需要往后移动,以过期元素
- 无论如何都是R先到达N - 1的位置的,那么我们需不需要等待L到达N -1的位置才结束呢?
- 不需要,因为每次元素入参,都会维护窗口的大小(L会改变),当R到达N - 1时,此时只有两种可能:窗口大小 < K,窗口大小 == K;
- 所以当R到达N-1的位置时,就可以跳出循环了。
- 因为窗口框住的是元素,所以L和R最多只能移动到N-1的位置
- 注意:L和R都是只往前移动,永远都不会往后退的
双端队列 - 最优解
维护一个滑动窗口并不难,但是我们需要解决一个问题:如何每次用非常小的代价求得滑动窗口的最大值。
简单方法是,每次都遍历一遍滑动窗口,但是这样代价就太高了,有没有一种结构让每次求得滑动窗口最大值的代价很小

我们可以用一个双端队列来实现这样的功能。我们用双端队列存放数组的下标,因为下标既可以得到数组的值,还可以得到值的位置,比单纯的放入数组的值得到的信息更多

因为我们要求最大值,所以双端队列从队头到队尾要保持下标对应的值是从大到小的。举个例子。
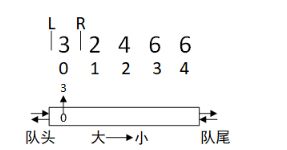
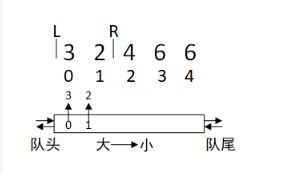
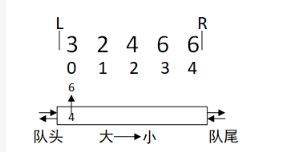
例子一: 模拟数组[3 2 4 6 6]滑动窗口R移动时双端队列的变化
1.R往右移动一个元素,3元素下标从队尾进队列。
3.R再往右移动一个元素,元素4的下标试图从队尾进入,但如果进入将破坏双端队列从队头到队尾从大大小的规则,所以元素2的下标1从队尾出队列(出队列后永远不找回),循环往复直到满足规则时从队尾放入。

4.R再往右移动一个元素。6比4大,因此4元素对应的下标先从队尾出,6元素的下标从队尾进。

5.R再往右移动一个元素。6和6相等,但因为要遵循严格单调性,6元素对应的下标3先从队尾出,6元素对应的下标4从队尾进。
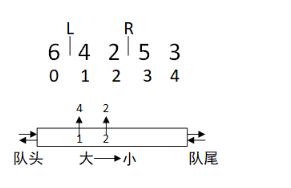
例子二: 模拟数组[6 4 2 5 3]滑动窗口L移动时队列的变化
1.初始状态

2.L往右移动一个元素,发现0是双端队列头部元素,0从队头弹出。
-
R向右移动时:如果双端队列队尾下标指向元素的值小于要弹入的值,则队尾依次弹出,直到队尾的值大于要弹入的值时,才弹入。(保持双端队列的严格单调性)。
-
L向右移动时:如果要弹出的值就是队头元素,则队头元素弹出;否则双端队列保持不变。
双端队列维持信息的意义是:我们不让R移动,而是让L依次移动的话,谁会依次成为最大值这个信息。
例子三: 模拟数组[1,3,-1,-3,5,3,6,7]滑动窗口L与R如何同时移动的变化
解释过程中队列中都是具体的值,方便理解,具体见代码。
初始状态:L=R=0,队列:{}
i=0,nums[0]=1。队列为空,直接加入。队列:{1}
i=1,nums[1]=3。队尾值为1,3>1,弹出队尾值,加入3。队列:{3}
i=2,nums[2]=-1。队尾值为3,-1<3,直接加入。队列:{3,-1}。此时窗口已经形成,L=0,R=2,result=[3]
i=3,nums[3]=-3。队尾值为-1,-3<-1,直接加入。队列:{3,-1,-3}。队首3对应的下标为1,L=1,R=3,有效。result=[3,3]
i=4,nums[4]=5。队尾值为-3,5>-3,依次弹出后加入。队列:{5}。此时L=2,R=4,有效。result=[3,3,5]
i=5,nums[5]=3。队尾值为5,3<5,直接加入。队列:{5,3}。此时L=3,R=5,有效。result=[3,3,5,5]
i=6,nums[6]=6。队尾值为3,6>3,依次弹出后加入。队列:{6}。此时L=4,R=6,有效。result=[3,3,5,5,6]
i=7,nums[7]=7。队尾值为6,7>6,弹出队尾值后加入。队列:{7}。此时L=5,R=7,有效。result=[3,3,5,5,6,7]
class Solution {
public:
vector<int> maxSlidingWindow(vector<int>& nums, int W) {
int N = nums.size();
if(W < 1 || N < W){
return {};
}
std::deque<int> qmax;// qmax 窗口最大值的更新结构
vector<int> ans; //vector ans(N - W + 1);
int idx = 0;
for (int R = 0; R < N; ++R) {
// 维护窗口
//1. R一定会入队,但是入队之前要把破坏结构的干掉(相等也要将其弹出因为他的小标比你晚过期不需要留你)
while (!qmax.empty() && nums[qmax.back()] <= nums[R]){
qmax.pop_back();
}
qmax.emplace_back(R); // 单调队列里面存的是数组下标
// 2. 检测头部数据是否是过期的数据
if(qmax.front() == R - W){
qmax.pop_front();
}
if (R >= W - 1) { //此时窗口已经形成
ans.emplace_back(nums[qmax.front()]);
}
}
return ans;
}
};
类似题目
| 题目 | 思路 |
|---|---|
| leetcode:239. 滑动窗口最大值 Sliding Window Maximum | |
| leetcode:155. 栈的最小值 Min Stack | |
| leetcode:159. 至多包含两个不同字符的最长子串 Longest Substring with At Most Two Distinct Characters | |
| [LeetCode] 727. Minimum Window Subsequence 最小窗口序列 | |
| leetcode:265. 粉刷房子(K个颜色可选) II |