算法通关村 | 第四关 | “栈”起来了啊~(黄金篇)
本篇文章是关于栈的最后一章,主要讲解一下栈中难以理解的一些问题,包括“表达式问题”,与部分滑动窗口(之后队列再讲)的知识,来吧,接着往下学一学!
计算器问题
先来个 “计算器” 算一算吧doge
227. 基本计算器 II - 力扣(LeetCode)
题目信息
给你一个字符串表达式
s,请你实现一个基本计算器来计算并返回它的值。整数除法仅保留整数部分。
你可以假设给定的表达式总是有效的。所有中间结果将在
[-231, 231 - 1]的范围内。注意:不允许使用任何将字符串作为数学表达式计算的内置函数,比如
eval()。输入:s = "3+2*2" 输出:7输入:s = " 3/2 " 输出:1
思路
这个计算器的问题只有加减乘除的运算和判断是否为空格,没有其他复杂的运算操作,最终我们要完成的目标为:
1、输入一个字符串,可以包含 + - * /、数字、括号以及空格,你的算法返回运算结果
2、要符合运算法则,括号的优先级最高,先乘除后加减
3、除号是整数除法,无论正负都向 0 取整(5/2=2,-5/2=-2)
乘除的优先级大于加减,对于加减号后的数字,直接压入栈中;对于乘除号后的数字,直接与栈顶元素进行计算,并替换栈顶元素为计算后的结果。
对于某个具体的字符串而言,用变量 preSign 记录数字之前的运算符,对于第一个其前面直接视为 + 号即可。每次遍历到数字的末尾时,按照 preSign 来决定计算方式。
+:数字入栈
-:将数字的 相反数入栈
* or /:计算数字与栈顶元素,将计算后的结果设为新的栈顶元素
值得注意的是:
num = num * 10 + s.charAt(i) - '0';1.以上代码之所以要 * 10 是因为,整数的十进制表示方式是每一位代表一个权重,从低位到高位权重依次增加,类似于10进制中的个位、十位、百位等。所以在字符串中的数字字符转换为整数后,需要将其放置在正确的位置。
比如举个例子,考虑字符串"123":
- 开始时,num的值为0。
- 遇到字符'1',将其转换为整数1,并赋值给num,此时num的值为1。
- 遇到字符'2',将其转换为整数2,并赋值给num,但这里需要注意,num之前已经是1了,所以需要将1左移一位(相当于乘以10),然后加上2,得到12。
- 遇到字符'3',将其转换为整数3,并赋值给num,同样需要将12左移一位(相当于乘以10),然后加上3,得到123。
2. - '0' 是因为,在ASCII码中,字符'0'对应的整数值是48。因此,当我们遇到一个数字字符比如'1'、'2'、'3'等,想要将其转换为对应的整数,可以通过减去字符'0'的整数值来实现。例子就不举了。
其他的也没啥了,还没看代码来的实在
代码如下
public int calculate(String s) {
Deque stack = new ArrayDeque<>();
char preSign = '+';
int num = 0;
int n = s.length();
for(int i = 0;i < n;i++){
// 把字符串转换成数字
if(Character.isDigit(s.charAt(i))){
num = num * 10 + s.charAt(i) - '0';
}
if(!Character.isDigit(s.charAt(i)) && s.charAt(i) != ' ' || i == n - 1){
switch (preSign) {
case '+':
stack.push(num);
break;
case '-':
stack.push(-num);
break;
case '*':
stack.push(stack.pop() * num);
break;
default:
stack.push(stack.pop() / num);
}
preSign = s.charAt(i);
num = 0;
}
}
int ans = 0;
while (!stack.isEmpty()) {
ans += stack.pop();
}
return ans;
} 这道题只是计算器问题中比较容易实现的,还有一些很困难得等我再研究研究做出一个专门讲解该问题的文章,这里就不再讲述了。
逆波兰表达式
这里也是以一道经典的题目为例,题目如下:
150. 逆波兰表达式求值 - 力扣(LeetCode)
给你一个字符串数组
tokens,表示一个根据 逆波兰表示法 表示的算术表达式。请你计算该表达式。返回一个表示表达式值的整数。
注意:
- 有效的算符为
'+'、'-'、'*'和'/'。- 每个操作数(运算对象)都可以是一个整数或者另一个表达式。
- 两个整数之间的除法总是 向零截断 。
- 表达式中不含除零运算。
- 输入是一个根据逆波兰表示法表示的算术表达式。
- 答案及所有中间计算结果可以用 32 位 整数表示。
输入:tokens = ["2","1","+","3","*"] 输出:9 解释:该算式转化为常见的中缀算术表达式为:((2 + 1) * 3) = 9输入:tokens = ["4","13","5","/","+"] 输出:6 解释:该算式转化为常见的中缀算术表达式为:(4 + (13 / 5)) = 6
什么是表达式
既类似于(1+2) * (3+4) 的式子,有前缀,中缀和后缀三种。区分如下:
- 中缀表达式:1+(2+3)×4-5
- 前缀表达式:-+1×+2345
- 后缀表达式:123+4×+5-
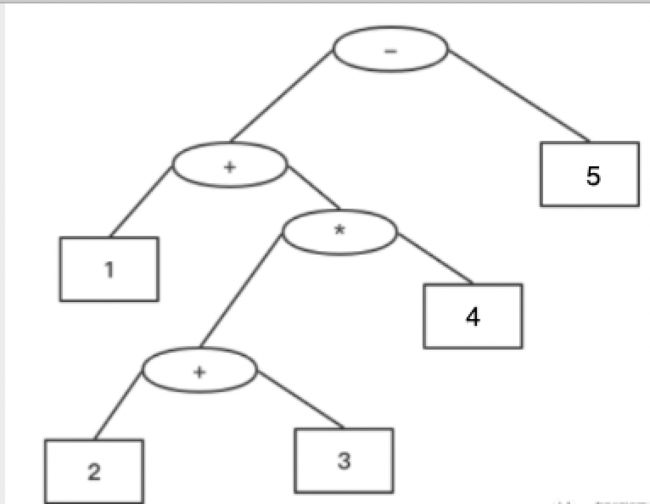
这里其实是与树息息相关的,相当于前中后序遍历,所谓的逆波兰表达式其实就是相当于二叉树中的后序遍历。我们可以把运算符作为中间结点,按照后序遍历画出一个二叉树,就如上图所示。
但是我们也不必从二叉树的角度去解决该问题,只要知道这个逆波兰表达式是使用后序遍历的方式把二叉树序列化了就行了。
再看看啥是逆波兰表达式:
逆波兰表达式:是一种后缀表达式,所谓后缀就是指运算符写在后面。
平常使用的算式则是一种中缀表达式,如 ( 1 + 2 ) * ( 3 + 4 ) 。
该算式的逆波兰表达式写法为 ( ( 1 2 + ) ( 3 4 + ) * ) 。
逆波兰表达式主要有以下两个优点:
去掉括号后表达式无歧义,上式即便写成 1 2 + 3 4 + * 也可以依据次序计算出正确结果。
适合用栈操作运算:遇到数字则入栈;遇到运算符则取出栈顶两个数字进行计算,并将结果压入栈中。
对于本题我们进一步看,对于每一个子表达式我们都有求出一个结果,然后再拿着这个结果进行计算。这我就想起来了这道经典的题,1047. 删除字符串中的所有相邻重复项 - 力扣(LeetCode)
好了铺垫结束,代码如下:
public int evalRPN (String[] tokens) {
// write code here’
Deque stack = new LinkedList<>();
// 处理符号
for(String s : tokens){
if("+".equals(s)){
stack.push(stack.pop()+stack.pop());
}else if("-".equals(s)){
stack.push(-stack.pop()+stack.pop());
}else if("*".equals(s)){
stack.push(stack.pop()*stack.pop());
}else if("/".equals(s)){
int tmp1 = stack.pop();
int tmp2 = stack.pop();
stack.push(tmp2/tmp1);
}else{
stack.push(Integer.valueOf(s)); // 字符串转成int直接入栈
}
}
return stack.pop();
}