手写数字识别--神经网络实验
实验源码自取:
神经网络实验报告源码.zip - 蓝奏云
上深度学习的课程,老师布置了一个经典的实验报告,我做了好久才搞懂,所以把实验报告放到CSDN保存,自己忘了方便查阅,也为其他人提供借鉴
由于本人是小白,刚入门炼丹,有写地方搞不懂,实验报告有错误的在所难免,请及时指出错误的地方
前馈神经网络的设计
一、实验目标及要求
1.掌握python编程
2.掌握神经网络原理
3. 掌握numpy库的基本使用方法
4. 掌握pytorch的基本使用
前馈神经网络是学习神经网络的基础。本实验针对MNIST手写数字识别数据集,设计实现一个基本的前馈神经网络模型,要求如下:
1. 在PyCharm平台上,分别基于numpy库和PyTorch实现两个版本的模型。
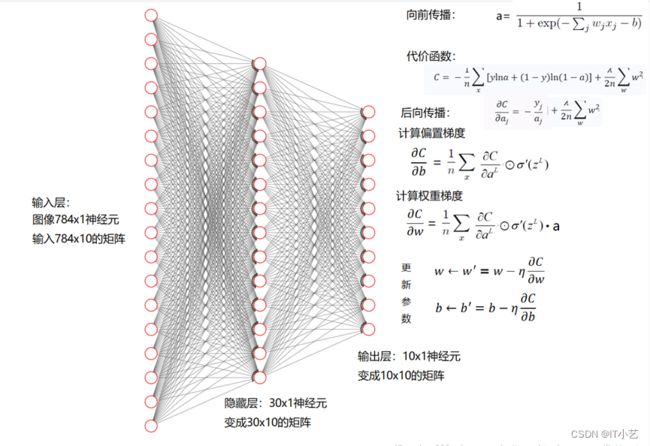
2. 网络包含一个输入层、一个输出层,以及k个隐藏层(1≤k≤3![]() )。
)。
3. 每个版本的项目文件夹里面有一个文件夹以及三个文件,文件夹名为data,存放MNIST数据集,三个文件为: main.py、network.py、 data_loader.py。main为主文件,通过运行main启动手写数字识别程序;network.py存放神经网络类定义及相关函数;data_loader.py存放负责读入数据的相关方法。
4. 原训练集重新划分为训练集(5万样本)、验证集(1万样本),原测试集(1万样本)作为测试集。
5. 模型中使用交叉熵代价函数和L2正则化项。
6. 在每一个epoch(假设为第i个epoch)中,用训练数据训练网络后,首先用验证集数据进行评估,假设验证集的历史最佳准确率为p![]() ,本次epoch得到的准确率为pi
,本次epoch得到的准确率为pi![]() ,如果pi>p
,如果pi>p![]() ,则用测试集评估模型性能,并把p更新为pi
,则用测试集评估模型性能,并把p更新为pi![]() ;否则不评估并且p不更新
;否则不评估并且p不更新![]() ,进行第i+1个epoch的训练。
,进行第i+1个epoch的训练。
7. 假设学习率固定为0.01,通过实验,评估不同的隐藏层个数k,以及隐藏层神经元个数m对模型性能的影响,找到你认为最好的k和m。
二、实验过程(含错误调试)
1.基于numpy库的模型
打开并统计数据集,发现训练集有50000个,验证集有10000个,测试集有10000个
对训练集输入的28x28图像矩阵转成784x1的列形状,把目标转成长度为10的列向量
对测试集和验证集输入的28x28图像矩阵转成784x1的列形状,目标保持不变
把数据传进模型,进行训练和测试
根据实验要求,定义Network类,实现初始化网络、前向传播、反向传播,更新参数,验证模型,测试模型,继续迭代,寻找最优参数。
import random
import numpy as np
# https://zhuanlan.zhihu.com/p/148102828
class Network(object):
def __init__(self, sizes):
self.num_layers = len(sizes)
self.sizes = sizes
self.biases = [np.random.randn(y, 1) for y in sizes[1:]] # randn,随机正态分布
self.weights = [np.random.randn(y, x) for x, y in zip(sizes[:-1], sizes[1:])]
self.lmbda = 0.1 # L2正则化参数
def feedforward(self, a):
for b, w in zip(self.biases, self.weights):
a = sigmoid(np.dot(w, a) + b)
return a
# 重复训练epochs次,训练集mini_batch_size个一包,学习率步长
def SGD(self, training_data, epochs, mini_batch_size, eta, val_data,test_data=None):
n_test = len(test_data)
n = len(training_data)
n_val = len(val_data)
best_accuracy = 0
for j in range(epochs): # 重复训练的次数
random.shuffle(training_data) # 随机打乱训练集顺序
mini_batches = [
training_data[k:k + mini_batch_size] # 切分成每批10个一组
for k in range(0, n, mini_batch_size)]
for mini_batch in mini_batches:
self.update_mini_batch(mini_batch, eta) # TODO
# 一次训练完毕
val_accuracy = self.evaluate(val_data) / n_val # 进行验证
# if j==1:
# print(f"参数m={m}训练第二次时,验证集精度{val_accuracy * 100}% ")
if val_accuracy > best_accuracy:
best_accuracy = val_accuracy
test_num = self.evaluate(test_data) # 进行测试
print(f"迭代次数: {j + 1},验证集精度{best_accuracy * 100}% ,测试集预测准确率: {(test_num / n_test) * 100}%")
else:
print(f'迭代次数:{j + 1},验证精度比前面那个小了,不进行测试')
# return val_accuracy
def update_mini_batch(self, mini_batch, eta):
m = len(mini_batch)
x_matrix = np.zeros((784, m))
y_matrix = np.zeros((10, m))
for i in range(m): # 初始化矩阵为输入的10个x,一次计算
x_matrix[:, i] = mini_batch[i][0].flatten() # 将多维数组转换为一维数组
y_matrix[:, i] = mini_batch[i][1].flatten()
self.backprop_matrix(x_matrix, y_matrix, m, eta)
def backprop_matrix(self, x, y, m, eta):
# 生成梯度矩阵,初始为全零
nabla_b = [np.zeros(b.shape) for b in self.biases]
nabla_w = [np.zeros(w.shape) for w in self.weights]
# 前向传播
activation = x
activations = [x] # 各层的激活值矩阵
zs = [] # 各层的带权输入矩阵
for w, b in zip(self.weights, self.biases):
z = np.dot(w, activation) + b
activation = sigmoid(z)
zs.append(z)
activations.append(activation)
# 后向传播
# 计算输出层误差, # 加上L2正则化
delta = (self.cross_entropy_cost_derivative(activations[-1], y) +
self.L2_regularization(self.weights[-1], m)) * sigmoid_prime(zs[-1])
# 计算输出层的偏置、权重梯度
nabla_b[-1] = np.array([np.mean(delta, axis=1)]).transpose()
nabla_w[-1] = (np.dot(delta, activations[-2].transpose()) / m)
# 反向传播误差,并计算梯度
for l in range(2, self.num_layers):
z = zs[-l]
sp = sigmoid_prime(z)
delta = np.dot(self.weights[-l + 1].transpose(), delta) * sp
nabla_b[-l] = np.array([np.mean(delta, axis=1)]).transpose()
nabla_w[-l] = np.dot(delta, activations[-l - 1].transpose()) / m
for l in range(1, self.num_layers):
self.biases[-l] = self.biases[-l] - eta * nabla_b[-l]
self.weights[-l] = self.weights[-l] - eta * nabla_w[-l]
def evaluate(self, test_data):
test_results = [(np.argmax(self.feedforward(x)), y) # argmax()找到数组中最大值的索引
for (x, y) in test_data]
return sum(int(x == y) for (x, y) in test_results)
def L2_regularization(self, weights, m):
return (self.lmbda / (m * 2)) * np.sum(np.square(weights))
def cross_entropy_cost_derivative(self, a, y):
# a是预测值矩阵,y是真实值矩阵
epsilon = 1e-7
a = a + epsilon # 防止除0错误
dc = -y / a # 交叉熵代价函数的导数
return dc
def sigmoid(z):
if np.all(z >= 0): # 对sigmoid函数优化,避免出现极大的数据溢出
return 1.0 / (1.0 + np.exp(-z))
else:
return np.exp(z) / (1 + np.exp(z))
# 求导sigmoid函数
def sigmoid_prime(z):
return sigmoid(z) * (1 - sigmoid(z))
# def cross_entropy_cost(a, y):
# # a是预测值矩阵,y是真实值矩阵
# n = a.shape[1] # 样本数量
# return -np.sum(y * np.log(a)) / n # 交叉熵代价函数
#
#
# def relu(z):
# return np.maximum(0, z)
#
#
# def relu_prime(z):
# # return np.array(x > 0, dtype=x.dtype)
# return (z > 0).astype(int) # relu函数的导数
# # 交叉熵代价函数和L2正则化项 -(self.lmbda / m) * self.weights[-1] # 加入L2正则化项
#
# def cost_function(output_activations, y):
# return np.sum(np.nan_to_num(-y * np.log(output_activations) - (1 - y) * np.log(1 - output_activations)))
# def L2_regularization(self, lmbda, weights):
# return lmbda * np.sum(np.square(weights)) / 2.0
#
# def cost_function_with_regularization(output_activations, y, weights, lmbda):
# return cost_function(output_activations, y) + L2_regularization(lmbda, weights)
在交叉熵代价函数求导后加上L2正则化,先衰减偏置,再衰减权重,防止过拟合
# 后向传播
# 计算输出层误差, # 加上L2正则化
delta = (self.cross_entropy_cost_derivative(activations[-1], y) +
self.L2_regularization(self.weights[-1], m)) * sigmoid_prime(zs[-1])
# 计算输出层的偏置、权重梯度
nabla_b[-1] = np.array([np.mean(delta, axis=1)]).transpose()
nabla_w[-1] = (np.dot(delta, activations[-2].transpose()) / m)
在大范围的改变学习率时,运行报错,
RuntimeWarning: overflow encountered in exp return 1.0 / (1 + np.exp(-x))
参照网上的做法,对sigmoid函数的x做判断,if np.all(x>=0): #对sigmoid函数优化,避免出现极大的数据溢出
return 1.0 / (1 + np.exp(-x))
else:
return np.exp(x)/(1+np.exp(x))
写交叉熵代价函数的导数时出现除0错误,于是对a加上很小的数
def cross_entropy_cost_derivative(self, a, y):
# a是预测值矩阵,y是真实值矩阵
epsilon = 1e-7
a = a + epsilon # 防止除0错误
dc = -y / a # 交叉熵代价函数的导数
return dc
2.基于PyTorch模型
打开并统计数据集,发现训练集有50000个,验证集有10000个,测试集有10000个
对数据集的图像矩阵转成浮点型的张量,对目标转成长整型的张量
把图像张量和目标张量一一对应放到 TensorDataset()函数转成数据对象,然后调用DataLoader()函数分批打包数据,生成迭代器对象
把数据传进模型,进行训练和测试
定义Net类,继承Model类,实现初始化网络、定义网络每一层的对象放入列表,前向传播、把输入传进每一层对象、最后一层调用log_softmax()函数进行归一化; 输入训练数据进行前向传播,把结果放进交叉熵损失函数、后向传播计算梯度,更新参数,验证模型,测试模型,继续迭代,寻找最优参数
处理数据集的时候把图像和目标都转成浮点张量torch.Tensor(),然后报错,网上找原因,需要把目标转成 长整型的张量,因为使用交叉熵损失函数进行训练时,需要将标签转换为整数编码。y=LongTensor(y),以便进行后续的计算,而模型中并没有使用y=LongTensor(y)函数,则需要提前将目标转成长整型张量
train_images, train_labels = torch.tensor(tr_d[0], dtype=torch.float32), torch.tensor(tr_d[1], dtype=torch.long)在处理数据集的时候,直接把张量放到DataLoader()里,然后报错了,查了书本后发现DataLoader()要传入dataset对象,需要把张量对应传入TensorDataset()函数生成dataset对象
train_dataset = TensorDataset(train_images, train_labels)
-
三、对实验中参数和结果的分析
1.基于numpy库的模型
当使用默认参数:sizes=[784,30,10] ,epochs=30,mini_batch_size=10,
Lmbda=0.1 ,eta=1.3时
测试最高精度是94.3%
运行时间79s
根据实验要求,分析不同隐藏层个数k和隐藏层神经元个数m对模型性能的影响:
由于我的电脑不太行,训练不同隐藏层个数k和隐藏层神经元个数m对模型性能的影响的时候需要很多时间,因此只训练2次出结果,结果可能会有偶然性。
当epochs=2,mini_batch_size=10,
Lmbda=0.1 ,eta=0.01,当只用一层隐藏层时,测试不同的神经元m对模型精度的影响,代码和结果如下
# 当隐藏层k=1时
accuracy_list=[]
for m in range(10,784):
net = Network([784,m, 10])
accuracy=net.SGD(training_data, 2, 10, 0.01, validation_data,m,test_data=test_data)
accuracy_list.append(accuracy)
x = range(10, 784)
max_acc=max(accuracy_list)
max_index = accuracy_list.index(max_acc)
print(f"当神经元m={10+max_index} 时,验证精度最大值为:{max_acc}")
plt.plot(x, accuracy_list)
plt.xlabel('m')
plt.ylabel('val_accuracy')
plt.show()
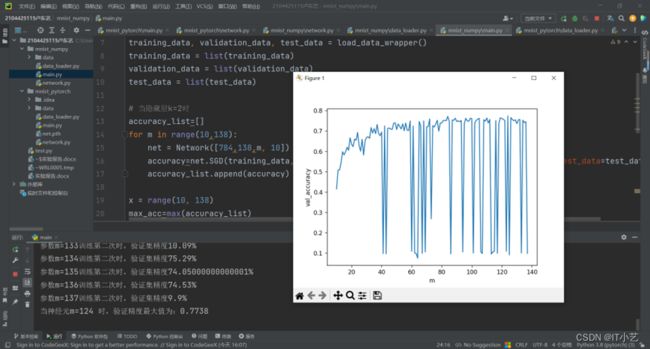
当运行到m=297 时,就卡住了,因此只讨论10到297个神经元的结果:
当只用一层隐藏层,神经元个数为138时,验证集精度最高,为77.92%
当用两层隐藏层时,测试不同的神经元m对模型精度的影响,由于组合次数太多,不可能每个神经元都训练,因此固定第一个隐藏层为138,神经元个数逐层递减进行训练,代码和结果如下
......
当有两层隐藏层,[784,138,m,10],神经元个数为124时,验证集精度最高,为77.38%
当用三层隐藏层时,测试不同的神经元m对模型精度的影响,由于组合次数太多,不可能每个神经元都训练,因此固定第一个隐藏层为138,神经元个数逐层递减进行训练,代码和结果如下
........
当有三层隐藏层,[784,138,124,m,10],神经元个数为118时,验证集精度最高,为76.18%
根据以上结果,当学习率固定为0.01时,我认为模型最好的k是1 ,m是138,精度77.92%,因为增加层数后验证集精度并没有多大提升,反而浪费了时间, 有点奇怪,也可能是模型有点问题
学习率固定为0.01,可能学习率小,步长小,迭代30次精度才77%左右,当学习率为默认的1.3时,精度才快速到94%
2.基于PyTorch模型
当使用默认参数:layers=[784,30,10] ,epochs=30,mini_batch_size=10,
,lr=0.01,weight_decay=0.0001时
测试最高精度是93.17%
运行时间171s
根据实验要求,分析不同隐藏层个数k和隐藏层神经元个数m对模型性能的影响:
由于我的电脑不太行,训练不同隐藏层个数k和隐藏层神经元个数m对模型性能的影响的时候需要很多时间,因此只训练2次出结果,结果可能会有偶然性。
当epochs=2,mini_batch_size=10,
lr=0.01,weight_decay=0.0001时,当只用一层隐藏层时,测试不同的神经元m对模型精度的影响,代码和结果如下
# 当隐藏层k=1时
accuracy_list=[]
for m in range(10,298):
net = Net([784,m, 10])
accuracy=train_and_test_net(net,training_data,validation_data,test_data,2,0.01,0.0001,m)
accuracy_list.append(accuracy)
x = range(10,298)
max_acc=max(accuracy_list)
max_index = accuracy_list.index(max_acc)
print(f"当神经元m={10+max_index} 时,验证精度最大值为:{max_acc}")
plt.plot(x, accuracy_list)
plt.xlabel('m')
plt.ylabel('val_accuracy')
plt.show()
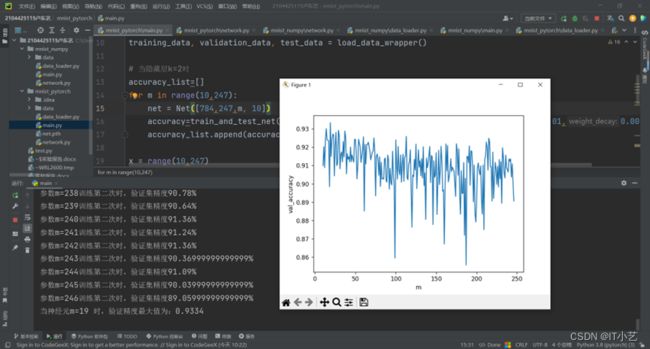
结果:当只用一层隐藏层,神经元个数为247时,验证集精度最高,为93.51%
当用两层隐藏层时,测试不同的神经元m对模型精度的影响,由于组合次数太多,不可能每个神经元都训练,因此固定第一个隐藏层为138,神经元个数逐层递减进行训练,代码和结果如下
......
结果: 当有两层隐藏层,[784,247,m,10],神经元个数为19时,验证集精度最高,为93.34%
当用三层隐藏层时,测试不同的神经元m对模型精度的影响,由于组合次数太多,不可能每个神经元都训练,因此固定第一个隐藏层为138,神经元个数逐层递减进行训练,代码和结果如下
.......
结果:当有三层隐藏层,[784,247,19,m,10],神经元个数为14时,验证集精度最高,为83.91%
根据以上结果,当学习率固定为0.01时,我认为模型最好的k是1 ,m是247,精度93.51%,因为增加层数后验证集精度并没有多大提升,反而浪费了时间和内存
四、两个模型的对比
基于numpy库的模型:
当使用默认参数:sizes=[784,30,10] ,epochs=30,mini_batch_size=10,
Lmbda=0.1 ,eta=1.3时
迭代30次后测试集最高精度是94.3%
运行时间79s
基于PyTorch模型
当使用默认参数:layers=[784,30,10] ,epochs=30,mini_batch_size=10,
,lr=0.01,weight_decay=0.0001时
测试最高精度是93.17%
运行时间171s
由此可见基于numpy库训练的模型比基于PyTorch的模型好,测试精度高,用的时间也少
基于numpy库的模型比较偏向底层,实现难,代码复杂,但运行速度快;基于PyTorch模型实现方式比较简单,代码比较简洁,但底层比较复杂,运行速度慢
训练神经网络模型首选PyTorch框架
五、总结
学会了很多,收获了很多,普通电脑只能训练小模型,以后遇到中模型肯定要用各大云平台的算力进行训练。
........................