SPSS PRO工具适用模型与辅助工具
内容或参考来源
https://www.spsspro.com/
数据预处理【工具】
数据标签
输入:一项定类变量。
输出:定类变量的文本标签修改。
数据编码
输入:一项定量或定类变量。
输出:对变量每个值进行重新编码。
异常值处理
详细解释

异常值可能是与整体数据情况偏离很大的数据点(常见的3σ准则),也可能在超过某个不合理范围的数据点,在分析中应该首先排除掉异常值,该方法可检测变量中的异常值,并对异常值进行置空或者是填补为其它有效值。
输入输出描述
输入:一项或以上的定量变量。
输出:对异常值置空或者是对异常值进行填补。
无效样本处理
详细解释
个案处理即按要求识别到满足条件的样本,并对其进行标记或者剔除。
输入输出描述
输入:两项及以上的定量或定类变量。
输出:对满足条件的样本进行删除或是标记(生成标记变量)。
生成变量
详细解释
生成变量是对单变量或多变量进行计算。其中平均值、求和、乘积(交互项)是多变量计算,即对多个变量的均值、加和、乘积的结果;自然对数、Log10是单变量计算,即对单个变量的数据的值进行计算。
输入输出描述
输入:对于平均值、求和、乘积(交互项):至少2个定量变量;对于自然对数、Log10:仅1个定量变量。
输出:按照选项计算生成新变量。
数据标准化
详细解释
数据标准化包括去量纲化和一致化。去量纲化是指不同指标之间由于量纲不同以致于其不具可比性,故首先需将指标进行无量纲化,消除量纲影响后再进行接下来的分析。例如,某个变量的数值在1-10之间,而另一个变量的数值范围在100-1000之间,此时若进行综合评价,从数值的角度,很有可能数值变化范围大的变量,它的绝对作用就会较大,所占的比重较大。一致性是指将指标作用方向一致化,例如我们在评价多个不同指标的作用时,正向指标是数值越大越好,负向指标是数值越小越好,如果同时评价这两类指标的综合作用,由于他们的作用方向不同,不能将指标作用直接相加,此时我们就需要对逆指标进行一致化处理。
输入输出描述
输入:一项或以上定量变量。
输出:新生成标准化后的变量。
虚拟变量转换
详细解释
多分类变量是不能直接参与到回归计算中。对于有序定类变量,可以将它进行数据编码,利用数字来表示分类变量的有序等级;但是对于无序定类变量,需要将其转变为虚拟变量来处理。虚拟变量转换包括哑变量和独热编码,其中哑变量化比独热编码少了一列变量,这是因为独热编码容易造成共线性,而哑变量随机以一个选项作为参照项,下图例子以”其它“作为参照项,当学生=0且上班族=0时,很明显,此时就默认归为”其它“,且在对回归系数进行解释时,所有类别哑变量的回归系数,均表示该哑变量与参照项相比之后对因变量的影响。 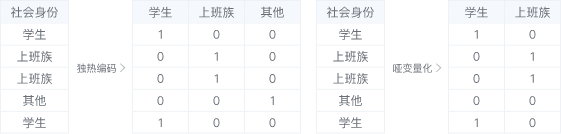
输入输出描述
输入:一项定类变量。
输出:新生成哑变量或者独热编码。
缺失值处理
详细解释
缺失值即空值,该方法可以识对各个变量的空值进行识别和填补,其中包括统计量填补和规则填补。
输入输出描述
输入:一项或以上定量或定类变量。
输出:对缺失值进行填补。
时序数据滑动窗口转换
详细解释
时序数据滑窗转换用于将时间序列数据转为回归数据,简单地说,就是把一个单序列的数据变为X->Y的回归数据。如下图所示,步阶为2代表2个X(步阶多少就有多少个X),简单地说,就是用第1,2天的数据预测第3天,用第2,3天的数据预测第4天,以此类推。此种形式的数据进行回归就是时间序列预测问题。 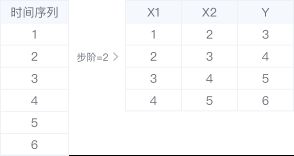
输入输出描述
输入:一项定量变量。
输出:根据步阶划分的自变量和因变量。
缩尾/截尾处理
详细解释
样本数据足够多时为了剔除一些极端值对研究的影响,一般会对连续变量进行缩尾/截尾处理。首先对变量数值进行从小到大排列后,处理超出变量特定百分位范围的数值(被称作极端值)。缩尾是将这些极端值替换为其特定数值,截尾是直接删除这些极端值。 
输入输出描述
输入:一项或以上定量变量。
输出:对极端值进行缩尾(填补)或截尾(删除)处理。
数据变换
数据变换是将数据准换成更适合数据分析的形式。其中Box-Cox变换的目的是为了让数据满足线性模型的基本假定。而小波变换和傅里叶变换能有效地提取相关的数据进行:小波变换可以同时提取时域信息和频域信息,而傅里叶变换只能提取频域信息。 
示例:
在使用线性回归的时候,由于残差不符合正态分布而不满足建模的条件,这时候要对因变量Y进行Box-Cox变换,把数据变成正态的,可以一定程度上减小残差和预测变量的相关性。
输入输出描述
输入:一项定量变量。
输出:变换后的新序列。
样本均衡
详细解释
进行分类任务时,如果因变量不同类别的样本数量不均衡时,会严重影响模型训练。比如说对于一个二分类问题,某一类别有995个数据,另一类别有5个数据时,此时属于严重的数据样本分布不均衡,很难从中提取规律,所以当发现样本不均衡时,需要做样本均衡处理,增加样本量较少的类别样本或减少样本量较多的类别样本,从而使得因变量不同类别的样本数量相差不大。 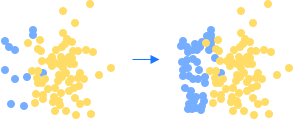
输入输出描述
输入:至少两项定量变量。
输出:增加样本量较少的类别样本或减少样本量较多的类别样本。
处理类型
过采样
- 随机法
- smote法
- ADASYN法
下采样
- 随机法
- Cluster Centroids法
组合采样
- SMOTE ENN法
- Tomek Link法
特征筛选
详细解释
特征数过多一方面增加了模型的复杂度,另一方面特征多也引入了更多的噪声数据,使模型更容易学到噪声,增大了发生过拟合的风险。所以变量(特征)过多时,需要从原始特征中选择出一些最有效特征以降低数据维度,从而有效提高模型性能。
输入输出描述
输入:至少两项定量变量。
输出:在变量名后标明应保留还是应剔除。
处理类型
- 方差选择法
- 随机森林特征重要度
- XGBoost
- 相关系数法
- 互信息法
- 卡方检验法
- VIF法
- 递归消除特征法
数据降维
详细解释
数据降维是采用某种映射方法,将原高维空间中的数据点映射到低维度的空间中,即将多列数据融合为更少列数据,且这些少列数据能够保留原数据的绝大部分有效信息。数据分析中存在部分变量是没有意义的,当这些无意义变量参与进分析的时候反而会对分析结果造成不利的影响,就可以进行降维处理;又或者想要对敏感隐私数据进行保护,也可进行降维来对数据进行变形整合。
输入输出描述
输入:至少两个定量变量(假设变量数为N)。
输出:新生成降维后的M个变量序列(M
处理类型
- PCA(主成分分析)
- LDA(线性判别法):
LDA是一种监督学习的降维技术,也就是说它的数据集的每个样本是有类别输出的。这点和PCA不同。PCA是不考虑样本类别输出的无监督降维技术。LDA的思想为投影后类内方差最小,类间方差最大,也就是数据在低维度上进行投影,投影后希望每一种类别数据的投影点尽可能的接近,而不同类别的数据的类别中心之间的距离尽可能的大。
-
ISOMap: 通过等距映射的非线性降维,是一种无监督算法。
-
LLE(局部线性嵌入算法): 和Isomap都属于流形学习方法。与Isomap不同的是,LLE在降维中,试图保持邻域内样本之间的线性关系,使得样本之间的映射坐标能够在低维空间中得以保持。
-
KPCA:
PCA只能是降维,把m维的数据降至k维。KPCA不仅可以降维,也可以升维,把m维的数据升至k维。他们共同的目标都是让数据在目标维度中(线性)可分,即PCA的最大可分性。
-
t-SNE: 用于在二维或三维的低维空间中表示高维数据集,从而使其可视化,与其他降维算法(如PCA)相比,t-SNE创建了一个缩小的特征空间,相似的样本由附近的点建模,不相似的样本由高概率的远点建模。
描述性分析(算法)
频数分析
详细解释
频数分析是对一组数据的不同数值的频数,或者数据落入指定区域内的频数进行统计,了解其数据分布状况的方式。通过频数分析,能在一定程度上反映出样本是否具有总体代表性,抽样是否存在系统偏差,并以此证明以后相关问题分析的代表性和可信性。
输入输出描述
输入:一个或多个定类变量。
输出:每个定类变量中不同类别样本的的分布状况与频数统计。
交叉分析
详细解释
用于分析两两分组变量之间的交叉分布,然后比较各组的分布状况,以寻找变量间的关系。 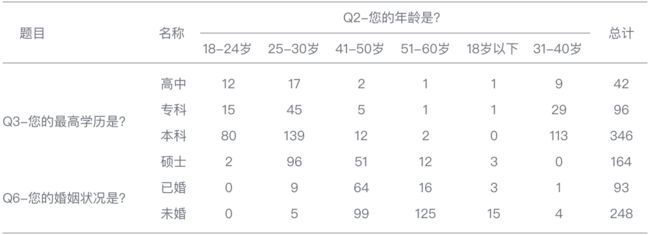
输入输出描述
输入:一个定类变量X与一个或者多个字段Y。
输出:两两分组变量之间的交叉分布情况。
描述性统计(e.g. boxplot)
详细解释
描述性统计分析是对调查总体所有变量的有关数据进行统计性描述,包括数据的集中趋势与离散趋势。
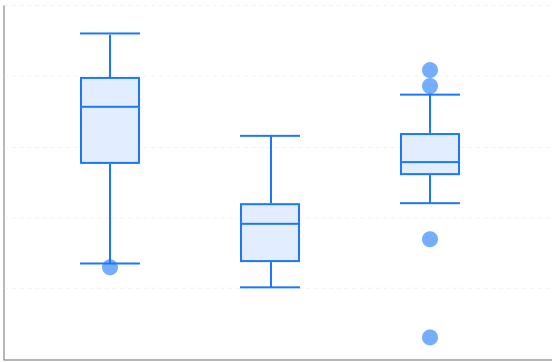
输入输出描述
输入:一个或多个定量变量。
输出:对总体数据的各项统计指标(字段)进行整体描述分析,包括样本量、最大值、最小值、算术平均值、中位数等统计量。
分类汇总
详细解释
根据定类变量分类进行汇总(按照某一标准进行分类,然后在分完类的基础上对各类别相关数据分别进行求和、求平均数、求个数、求最大值、求最小值等方法的汇总。又名列联表分析)。
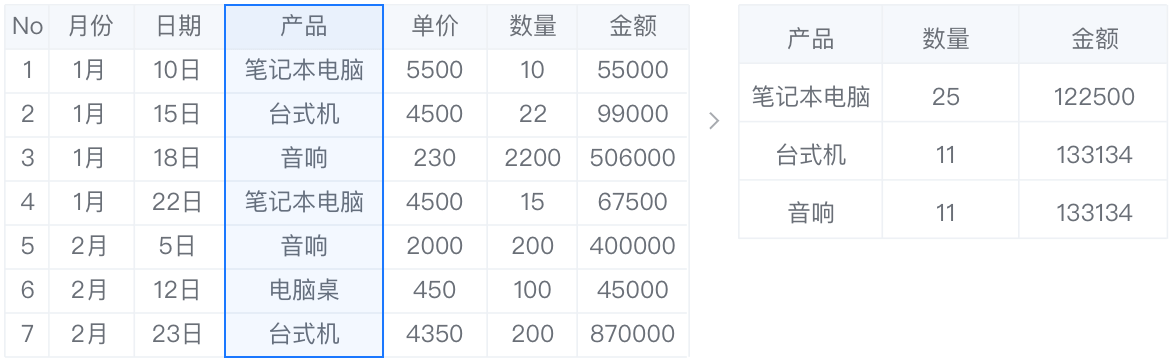
输入输出描述
输入:分组项为一个或多个定类变量,汇总项为一个或多个定类变量。
输出:在分完类的基础上对各类别相关数据分别进行求和、求平均数、求个数、求最大值、求最小值等统计量。
正态性检验
输入输出描述
输入:一个或多个定量变量(如30名员工这个月的工资)。
输出:模型检验的结果,数据满足/不满足正态分布。
综合评价【重点】
层次分析法(AHP)
详细解释
层次分析法是一种解决**多目标的复杂问题的定性与定量相结合的决策分析方法**。该方法将定量分析与定性分析结合起来,用决策者的经验判断**各衡量目标之间能否实现的标准之间的相对重要程度**,例如通过构建评价指标(景色、费用,居住,饮食、旅途)对候选旅游地(桂林、黄山,北戴河)量化评价,进行选择。在专业版里面,系统健全对方案层的层次总排序,如不需层次总排序,请选择层次分析法(AHP简化版)。
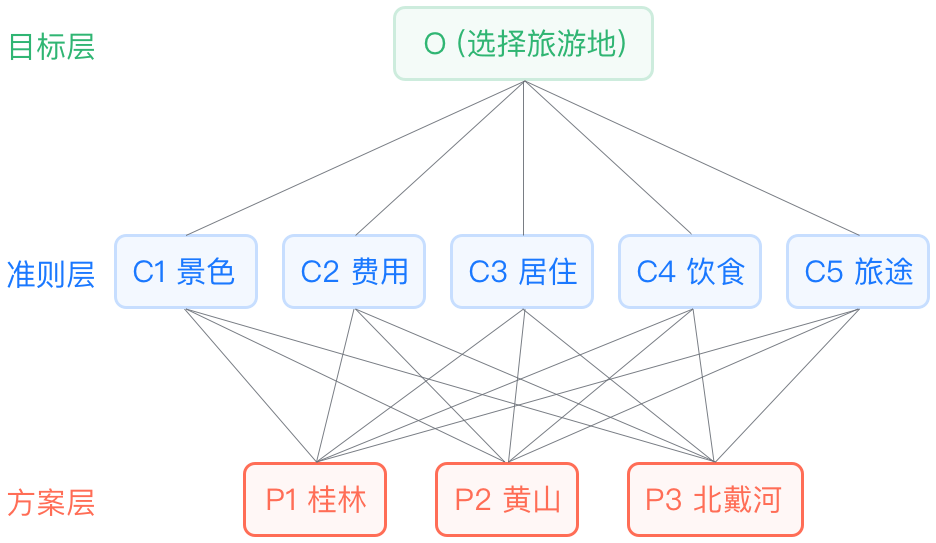
示例:
通过构建评价指标(景色、费用,居住,饮食、
旅途)对候选旅游地(桂林、黄山,北戴河)
量化评价,进行选择。
输入输出描述
输入:根据提示进行指标或者方案两两对比。
输出:各方案的量化得分或者同一级的指标权重。
因子分析(计算权重)
详细解释
因子分析是基于**降维**的思想,在尽可能不损失或者少损失原始数据信息的情况下,**将错综复杂的众多变量聚合成少数几个独立的公共因子**,这几个公共因子可以**反映原来众多变量的主要信息**,在减少变量个数的同时,又反映了变量之间的内在联系。通常因子分析有三种作用:一是用于**因子降维**,二是**计算因子权重**,三是**计算加权计算因子汇总综合得分**。
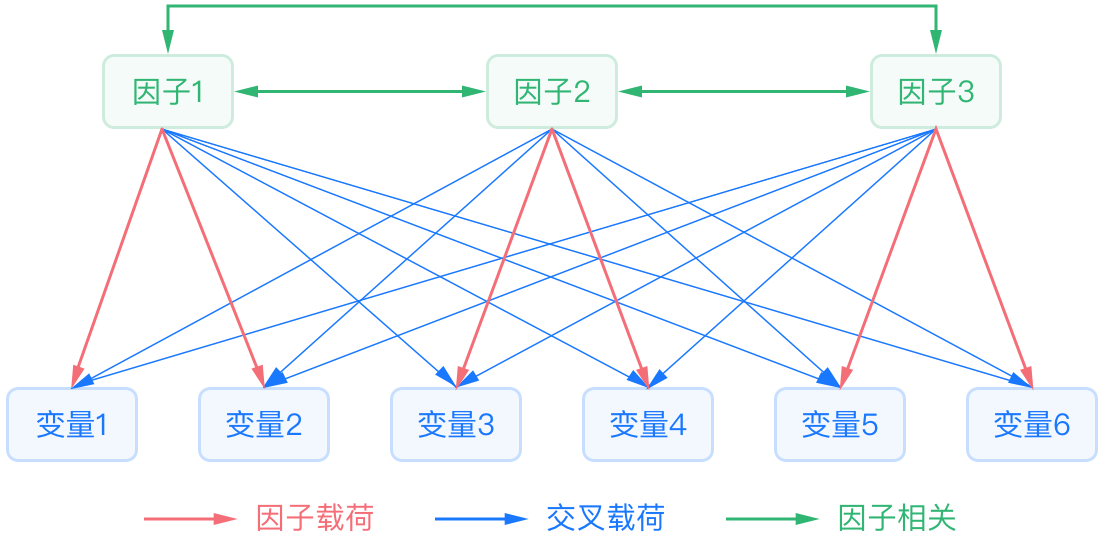
输入输出描述
输入:2个或两个以上的定量变量(假设为N个变量)。
输出:最低可降维成1维(一个变量,一般用于综合评价),最多可降维成N个变量(一般用于数据脱敏),同时可以获取降维后各个变量的组成权重,用于代表原先变量的数据保留情况。
数据包络分析(DEA)
详细解释
数据包络分析是**评价多输入指标和多输出指标**的较为有效的方法,**将多投入与多产出进行比较**,得到效率分析,可广泛使用于业绩评价。
输入输出描述
输入:数据包络分析的输入是投入、产出的指标(定量变量)。
输出:效率评估结果,包含具体需要增大或减小哪些投入变量,如何调整产出变量,才能达到最优效率。
模糊综合评价【重点】
详细解释
模糊综合评价借助模糊数学的一些概念,对实际的综合评价问题提供评价,即模糊综合评价以模糊数学为基础,应用模糊关系合成原理,将一些边界不清、不易定量的因素定量化,进而进行综合性评价的一种方法。
输入输出描述
输入:至少两项或以上的定量变量。
输出:反应考核指标在量化评价中的综合得分。
TOPSIS法(优劣解距离法)
详细解释
TOPSIS 法是一种常用的**组内综合评价**方法,能充分利用原始数据的信息,其结果能精确地反映**各评价方案之间的差距**。基本过程为基于归一化后的原始数据矩阵,采用余弦法找出有限方案中的最优方案和最劣方案,然后分别计算各评价对象与最优方案和最劣方案间的距离,获得各评价对象**与最优方案的相对接近程度**,以此作为评价优劣的依据。该方法对数据分布及样本含量没有严格限制,数据计算简单易行。
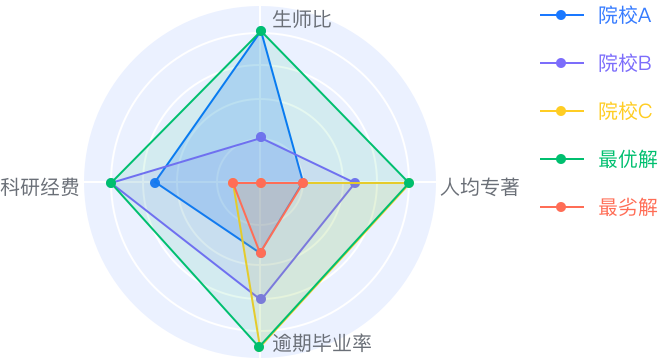
输入输出描述
输入:至少两项或以上的定量变量。
输出:反应考核指标在量化评价中的综合得分。
秩和比综合评价法(RSR)【用于效益-成本分析】
详细解释
秩和比(RSR)指将效益型指标从小到大排序进行排名、成本型指标从大到小排序进行排名,再计算秩和比,最后统计回归、分档排序。通过秩转换,获得无量纲统计量RSR,以RSR值对评价对象的优劣直接排序或分档排序,从而对评价对象做出综合评价。
输入输出描述
输入:至少两项或以上的定量变量。
输出:反应考核指标在量化评价中的综合得分(RSR)与分档。
耦合协调度
详细解释
耦合协调度模型用于分析事物的协调发展水平。耦合度指两个或两个以上系统之间的相互作用影响,实现协调发展的动态关联关系,可以反映系统之间的相互依赖相互制约程度。协调度指耦合相互作用关系中良性耦合程度的大小,它可体现出协调状况的好坏。
输入输出描述
输入:至少两项或以上的定量变量。
输出:以样本(行)为单位,各个单位综合各个变量的耦合协调程度。
多指标综合评价赋权系列
熵值法【多指标综合评价,计算指标权重】
详细解释
熵值法根据信息熵的定义,对于某项指标,可以用熵值来判断某个指标的离散程度,其信息熵值越小,**指标的离散程度越大, 该指标对综合评价的影响(即权重)就越大**,如果某项指标的值全部相等,则该指标在综合评价中不起作用。因此,可利用信息熵这个工具,计算出各个指标的权重,为**多指标综合评价**提供依据。
输入输出描述
输入:至少两项或以上的定量变量(正向指标与负向指标)。
输出:输入定量变量对应的权重值。
CRITIC权重法【多指标综合评价-减少指标堆叠时用】
详细解释
CRITIC权重法是一种客观赋权法。其思想在于用两项指标,分别是对比强度和冲突性指标。对比强度使用标准差进行表示,如果数据标准差越大说明波动越大,权重会越高;冲突性使用相关系数进行表示,如果指标之间的相关系数值越大,说明冲突性越小,那么其权重也就越低。对于多指标多对象的综合评价问题,CRITIC法去消除一些相关性较强的指标的影响,减少指标之间信息上的重叠,更有利于得到可信的评价结果。
输入输出描述
输入:至少两项或以上的定量变量(可以做正、负向处理,但是不要做标准化)。
输出:输入定量变量对应的权重值。
独立性权系数法【多指标综合评价-共线性】
详细解释
独立性权系数法是一种客观赋权法。其思想在于根据各指标与其他指标之间的共线性强弱来确定指标权重的,**若指标之间的共线性关系越强**,越容易由其他指标的线性组合表示,重复信息越多,因此**该指标的权重也就应该越小**。
输入输出描述
输入:至少两项或以上的定量变量。
输出:输入定量变量对应的权重值。
变异系数法【打分系统赋权】
详细解释
根据各评价指标当前值与目标值的变异程度来对各指标进行赋权,**当各指标现有值与目标值差距较大时,说明该指标较难实现目标值,应该赋予较大的权重,反之则应该赋予较小的权重**,其原理较为简单,通常用于专家评价打分的差异分析。
输入输出描述
输入:至少两项或以上的定量变量。
输出:输入定量变量对应的权重值。
灰色关联分析【单一目标指标的情况用】【常考】
详细解释
灰色关联分析是指对一个系统发展变化态势的定量描述和比较的方法,其基本思想是**通过确定参考数据列和若干个比较数据列的几何形状相似程度来判断其联系是否紧密,它反映了曲线间的关联程度**。
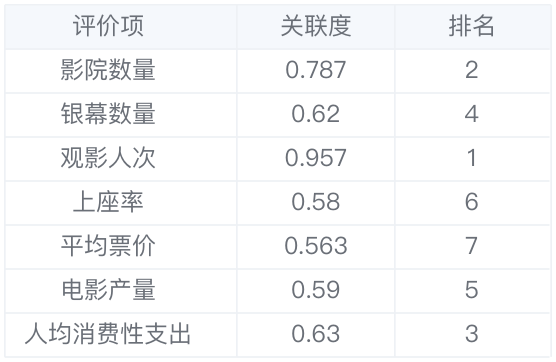
示例:
分析近10年内,影院数量,观影人数,上
座率,票价、电影上线数量等因素对全年
电影票房的影响。其中电影票房是母序
列,影院数量,观影人数,上座率,票
价、电影上线数量等因素是特征序列。
输入输出描述
输入:特征序列为至少两项或以上的定量变量,母序列(关联对象)为1项定量变量。
输出:反应考核指标与母序列的关联程度。
应用举例:寻求各项指标与年龄(母序列)的关系
| 关联度结果 | ||
|---|---|---|
| 评价项 | 关联度 | 排名 |
| 身高cm | 0.844 | 1 |
| 体重kg | 0.839 | 2 |
| 心率 | 0.799 | 3 |
| 夜宵情况 | 0.783 | 4 |
| 逛街情况 | 0.759 | 5 |
| 玩电脑游戏情况 | 0.748 | 6 |
| 日常锻炼情况 | 0.74 | 7 |
| 吃零食情况 | 0.697 | 8 |
多准则妥协解排序法(VIKOR模型,用于对评价对象排序,类似于TOPSIS法)
详细解释
VIKOR模型是一种**对评价对象进行排序**的方法。基本过程为**首先计算评价对象总的最优解和最差解**,然后比较各评价对象与最优解和最差解之间的距离大小来确定评价对象的排序,进而获得待评价对象的优劣级别。
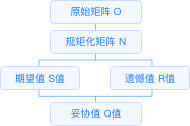
输入输出描述
输入:至少两项或以上的定量变量。
输出:反应考核指标在量化评价中的综合得分。
解释结构模型(SIM)
详细解释
解释结构模型(ISM)是一种系统分析方法,用于得到**要素之间的复杂相互关系和层次**。其思想是先通过调查或者技术手段找出问题的组成要素或影响因素,然后通过矩阵模型分析各要素之间的联系,得到一个多级递阶结构模型。
输入输出描述
输入:要素之间浅显的相互关系。
输出:要素之间复杂的相互关系和层次。
差异性分析自动求解器【工具】
详细解释
输入输出描述
输入:若干定类变量和定量变量。
输出:模型检验的结果。
差异性分析——参数检验
单样本T检验【正态性检验】
详细解释
单样本T检验用于比较样本数据与一个特定数值之间的差异情况,同时要求数据呈现正态性分布。 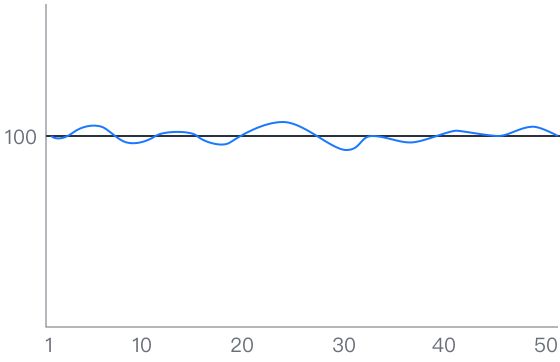
输入输出描述
输入:设定的检验值,如上示例的100,以及还有一个定量变量数据,如上示例的50瓶食品的重量。
输出:该定量变量数据是否与该特定数值分布呈现一致性。
配对样本T检验
详细解释
用于比较配对的连续变量X1与连续变量X2之间的差异情况,同时**要求配对变量差值呈现正态性分布**。
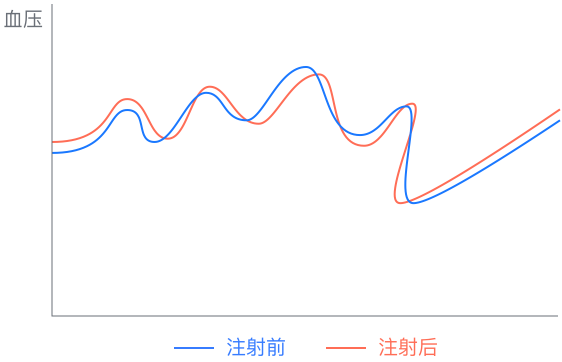
示例:
检验某医院30个病人注射某药剂前后血压是否一致。
输入输出描述
输入:样本数相同,且差值呈现正态分布的两个定量变量。
输出:这两个定量变量是否存在差异性。
独立样本T检验【分析一个二分类变量与定量变量之间有无明显差异】
详细解释
独立样本T检验用于分析**一个定类变量与一个或者多个定量变量之间有无明显差异**,需要特别注意的是,该定类变量为二分类变量(三分类及以上使用方差分析),各分类频数可以不相等。
输入输出描述
输入:一个定类变量X(如学校字段,包括甲学校、乙学校)与定量字段Y(如甲40名学生与乙学校60名学生的高考数学成绩)。
输出:模型检验的结果,如甲学校与乙学校的学生高考数学成绩存在/不存在显著性差异。
单因素方差分析(F检验)
详细解释
方差分析(单因素方差分析或F检验)用于**定类字段(X)与1个或1个以上的定量字段(Y)之间的差异性研究**。需要注意的是,一个定类字段称为单因素方差分析,两个定类字段及以上称为多因素方差分析,与独立样本T检验不同的是,方差分析可用于多分类定类字段数据的差异性分析,T检验只能作用于二分类定类变量。
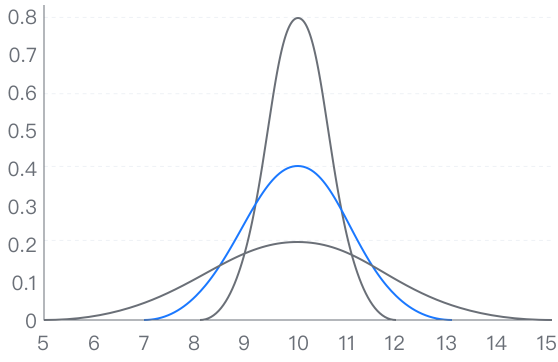
示例:
分析个人受教育程度(定类变量)是否给
个人的经济收入(定量变量)带来显著性
影响。
输入输出描述
输入:一个定类字段(如受教育程度)、一个或多个定量字段(如工资、家庭年收入)。
输出:模型检验的结果:同一因素不同分组(如:不同的受教育程度X)对定量变量(如:工资Y)产生/不产生显著性影响。
事后多重比较【基于方差分析】
详细解释
事后多重比较是指**方差分析后对各样本平均数间是否有显著差异的假设检验**的统称。方差分析只能判断各总体平均数间是否有差异,**多重比较可用来进一步确定哪两个平均数间有差异,哪两个平均数间没有差异**。
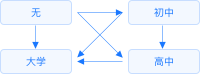
示例:
已知个人受教育程度给个人的经济收入存在显著性影响,分析不同受教育程度的具体影响情况如何。
输入输出描述
输入:一个定类分组字段以及一个或以上的定量字段。
输出:在同一因素不同分组对定量变量存在显著性影响时的具体差异情况。
双因素方差分析【两个定类因素是否决定定量结果】
详细解释
双因素方差分析是一种统计分析方法,可以用来分析**两个因素的不同水平对最终结果是否有显著影响**。且分为两种,**一种是无交互作用的双因素方差分析**,它假定因素A和因素B的效应之间是相互独立的。另一种是**有交互作用的双因素方差分析**,它假定因素A和因素B的结合会产生出一种新的效应。
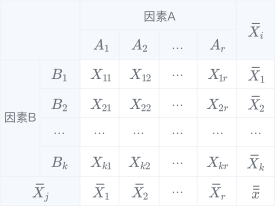
示例:
某研究机构分析主流品牌的智能手机
在四个地区销售的销售情况,分析手
机销售量是否由于品牌的不同和地区
的不同而存在差异。
输入输出描述
输入:两个分组定类字段和一个待分析定量字段,以及可选的协变量。
输出:两个因素的对结果是否显著影响,以及两因素之间的交互效应。
三因素方差分析【三个定类因素,一个定量结果】
详细解释
用来**分析三个因素的不同水平对最终结果是否有显著影响**。且分为两种,一种是无交互作用的三因素方差分析,它假定三个因素之间是相互独立的。另一种是有交互作用的三因素方差分析,它假定因素因素两两之间或三个因素之间会产生出一种新的效应。
输入输出描述
输入:三个分组定类字段和一个待分析定量字段,以及可选的协变量。
输出:三个因素的对结果是否显著影响,因素之间的交互效应。
多因素方差分析
输入:多个分组定类字段和一个待分析定量字段。
输出:多个因素的对结果是否显著影响。
摘要单因素方差分析【单因素方差分析缺少原始数据时用】
详细解释
一般进行**单因素方差分析**需要原始数据进行分析,但**有时没有原始数据,如数据缺失或者验证论文时。此时只有样本量,平均值,标准差这样的汇总数据**,可以使用摘要单因素方差分析检验差异是否显著。
示例:
验证三组病人的血糖是否存在差异性,但是数据缺失,只有汇总数据。一组病人(34人)的饭后血糖均值为4.63,标准差为0.8。一组(40人)的饭后血糖均值为 4.89,标准差为0.62。一组(36人),均值为4.78,标准差为 0.53。使用摘要单因素方差分析检验差异是否显著。
输入输出描述
输入:摘要数据(样本量、均值、标准差)以及对应的置信度级别。
输出:单因素方差分析的结果。
摘要T检验【T检验缺少原始数据时用】
详细解释
一般进行T检验需要原始数据进行分析,但有时没有原始数据,如数据缺失或者验证论文时。此时只有样本量,平均值,标准差这样的汇总数据,可以使用摘要数据T检验分析差异是否显著。
输入输出描述
输入:摘要数据(样本量、均值、标准差)以及对应的置信度级别。
输出:单样本T检验或者独立样本T检验的结果。
差异性分析——非参数检验
卡方检验【定类-定类之间的差异性分析】
详细解释
卡方检验主要是比较定类变量与定类变量之间的差异性分析。通过统计样本的实际观测值与理论推断值之间的偏离程度,实际观测值与理论推断值之间的偏离程度就决定卡方值的大小,如果卡方值越大,二者偏差程度越大;反之,二者偏差越小;若两个值完全相等时,卡方值就为0,表明理论值完全符合。 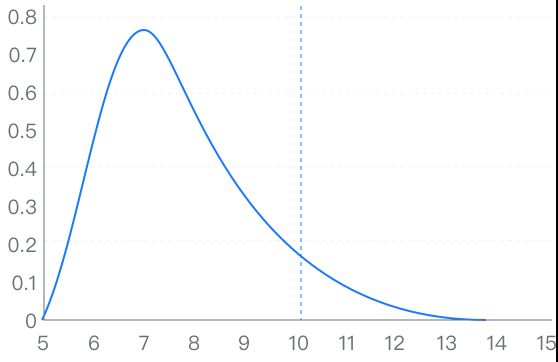
示例:
如从某高中学随机抽取两个以上的班级,
调查他们对待文理分科的态度是否有显著
差异。
输入输出描述
输入:一个定类变量X(如学校字段,包括甲学校、乙学校)与定类字段Y(如甲学校40名学生与乙学校60名学生的体育成绩等级)。
输出:模型检验的结果,如甲学校与乙学校的学生体育成绩等级存在/不存在显著性差异。
单样本Wilcoxon符号秩检验【非正态数据的“T检验”】
详细解释
单样本Wilcoxon符号秩检验用于比较样本数据中位数与一个特定数值之间的差异情况,与单样本T检验不同的是,它不需要数据呈现正态性分布。
输入输出描述
输入:设定的检验值,如上示例的100,以及还有一个定量变量数据,如上示例的50瓶食品的重量。
输出:该定量变量数据是否与该特定数值分布呈现一致性。
配对样本Wilcoxon符号秩检验【样本差值不呈现正态分布的配对T检验】
详细解释
配对样本Wilcoxon符号秩检验用于比较配对的连续变量X1与连续变量X2之间的差异情况,同时配对变量差值不呈现正态性分布。
输入输出描述
输入:样本数相同,且差值不呈现正态分布的两个定量变量。
输出:这两个定量变量是否存在差异性。
独立样本MannWhitney检验【非正态的独立样本T检验】
详细解释
MannWhitney检验用于分析**一个定类变量与一个或者多个定量变量之间有无明显差异**,与独立样本T检验不同的是,**MannWhitney检验不需要数据呈现正态分布**,需要特别注意的是,以上说到的**定类变量为二分类变量**(三分类及以上使用Kruskal-Wallis检验),各分类频数可以不相等。
输入输出描述
输入:一个定类变量X(如学校字段,包括甲学校、乙学校)与定量字段Y(如甲40名学生与乙学校60名学生的高考数学成绩)。
输出:模型检验的结果,如甲学校与乙学校的学生高考数学成绩存在/不存在显著性差异。
多配对样本Friedman检验【变量不符合正态分布时,替代方差分析】
详细解释
Friedman检验用于分析多组样本数一致的定量变量之间有无明显差异,需要特别注意的是,这些定量变量适用于非正态分布,如果变量数据呈现正态分布,建议选择方差分析。 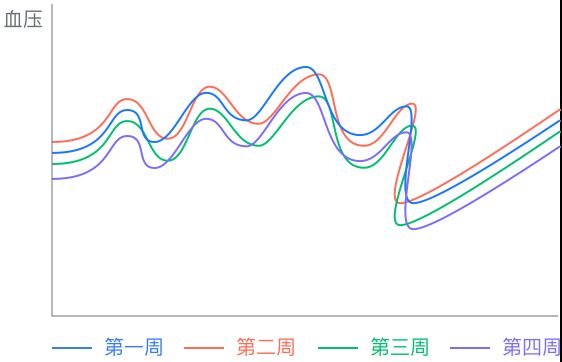
示例:
检验某医院300个病人注射某药剂第一、 二、三、四周的血压是否一致。
输入输出描述
输入:样本数相同,且不呈现正态分布的3个或者3个以上定量变量
输出:这些定量变量整体是否存在差异性,哪些变量两两之间存在差异,以及他们的差异程度怎样。
多独立样本Kruskal-Wallis检验【K-W检验】
详细解释
多独立样本Kruskal-Wallis检验用于定类字段(X)与1个或1个以上的定量字段(Y,不需要正态分布)之间的差异性研究。需要注意的是,Kruskal-Wallis检验可用于多分类定类字段数据的差异性分析,MannWhitney U检验只能作用于二分类定类变量。 
输入输出描述
输入:一个定类字段(如受教育程度)、一个或多个定量字段(如工资、家庭年收入)。
输出:模型检验的结果:同一因素不同分组(如:不同的受教育程度X)对定量变量(如:工资Y)产生/不产生显著性影响。
卡方拟合优度检验
详细解释
卡方拟合优度检验是基于卡方统计量用于判断期望频数与观察频数是否有显著差异。
输入输出描述
输入:各分组项的期望比例。
输出:判断收集的数据分布与预期是否呈显著性差异。
相关性分析自动求解器【工具】
详细解释
系统将根据拖入的变量提示可用的相关性分析方法,分为两两比对和总体比对两种,两两比对指分析变量两两之间的情况,而总体比对指分析全部变量整体的情况。 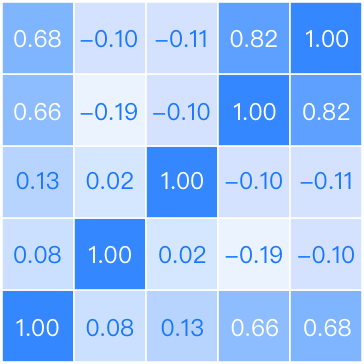
示例:
某人需要研究两个变量之间的相似情况,但是不知道该使用什么样的方法,在相关性分析自动求解器中拖入这两个变量,系统自动选择Spearman相关系数为他分析。
输入输出描述
输入:若干定类变量和定量变量。
输出:合适的相关性分析方法以及对应的结果。
相关性分析
Pearson相关性分析【正态双定量变量】
详细解释
Pearson相关性分析适用于服从正态分布的两定量变量,若两变量通过绘制散点图后发现存在线性趋势,可以通过计算Pearson相关系数来描述两变量的线性相关性。
输入输出描述
输入:两个或者两个以上的定量变量。
输出:两两变量之间是否呈现显著性相似以及相似的程度。
Spearman相关性分析【定量/定序变量两两之间,但尽量含定序时用】
详细解释
Spearman相关系数适用于定量变量或定序变量两两之间的相关分析,利用两变量的秩次大小作线性相关分析,对原始变量的分布不作要求,**当我们变量中至少存在一个有序变量时,可使用Spearman系数来描述两变量的相关性。**对于均为定量数据亦可计算Spearman相关系数,但统计效能要低一些。
输入输出描述
输入:两个或者两个以上的定量变量或有序定类变量(有序定类变量可用数值代替)。
输出:两两变量之间是否呈现显著性相似以及相似的程度。
Kendall’s tau-b相关性分析
详细解释
Kendall’s tau-b系数适用于定序变量两两之间相关分析,其不要求变量满足正态分布条件,当我们变量中均为有序变量时,可使用Kendall’s tau-b系数来分析变量间的相关性。
输入输出描述
输入:两个或者两个以上的有序定类变量(有序定类变量可用数值展示)。
输出:两两变量之间是否呈现显著性相似以及相似的程度。
Cochran’s Q检验
详细解释
Cochran’s Q 检验也是用于非参数差异性检验的一种,适用于分析多个样本(样本数一致)差异性的统计检验,用于三个字段以上的数据的总体差异性的统计检验。与Friedman检验与Nemenyi检验不一样的是,Cochran’s Q 检验只适用定类字段。 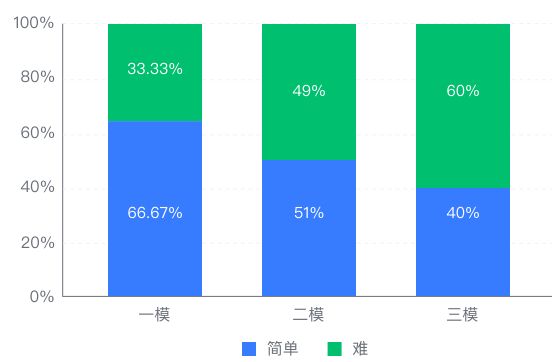
示例:
分析50个同学对一模、二模、三模的三次高考模拟
考试的体验,体验分为难或简单,检验三次考试难
度是否一样。
输入输出描述
输入:三个或以上的二分类定类变量变量。
输出:变量整体上是否呈现显著性差异。
Kappa一致性检验【两两定类数据的相关性检验】
详细解释
Kappa系数用于定类数据的相关性检验,而一般定量数据的相关性检验为皮尔逊相关系数。一般Kappa系数可用于衡量分类精度,或者投票等定类数据,kappa计算结果为[0, 1],可分为五组来表示不同级别的一致性:[0, 0.2]表现为极低的一致性、(0.2, 0.4]表现为一般的一致性、(0.4, 0.6]表现为中等的一致性、(0.6, 0.8]表现为高度的一致性和(0.8, 1]表现为几乎完全一致性。 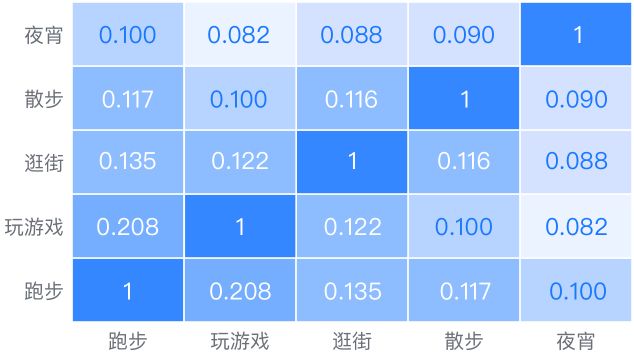
输入输出描述
输入:两个或以上的定类变量或有序定类变量,若为Flesis Kappa,则为三组以上的定类变量或有序定类变量。
输出:两两变量之间是否呈现显著性相似以及相似的程度,若为Flesis Kappa,则为变量整体的一致性程度。
Kendall一致性检验【总体定类数据的相关性检验】
详细解释
肯德尔(Kendall)系数用于定类数据的相关性检验,与此类似的有Kappa系数一致性检验。这两者不同的是:Kappa系数与皮尔逊一样是比较两项之间的相关性;而Kendall系数用于判断总体(全部数据)的相关性,适用于数据是多列相关的等级资料,即可是k个评分者评(N)个对象,也可以是同一个人先后k次评N个对象。通过求得kandall和谐系数,可以较为客观地选择好的作品或好的评分者。 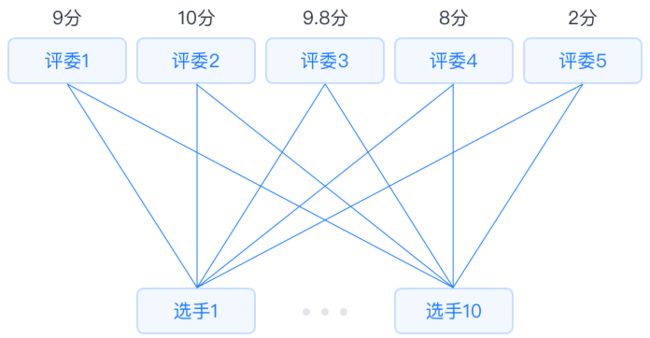
示例:
分析5个评委对10个选手的打分一致性程
度。
输入输出描述
输入:两组及两组以上。
输出:整体的一致性程度。
组内相关系数(ICC)
详细解释
组内相关系数(ICC)是衡量和评价观察者间信度和复测信度的信度系数指标。通常可以用于问卷调查中评价一个对象对多个样本在一段时间的重测信度,或者判断一批对象对多个样本的一致性检验。 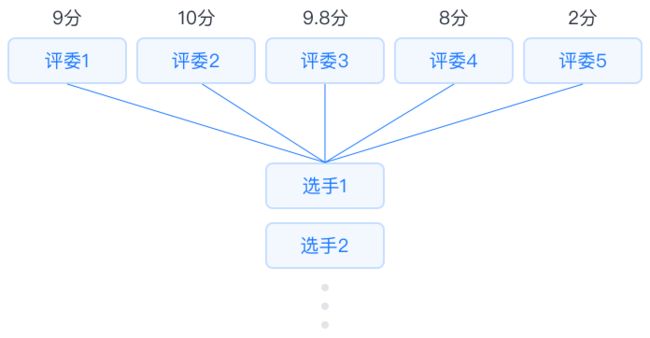
示例:
5个评委对于同一批选手进行评分,测量
其评分是否一致。或者测量复测信度,比
如多次收集某个评委对100个参赛选手的
评分(或同一批评委的评分平均值),测
量其每次评分的相关度是否一致。
输入输出描述
输入:至少两项或以上的定量变量或有序的定类变量,一般要求数据为量表量数据。
输出:设计的问卷量表题目里各样本是否具有一致性。
预测模型【重点】
线性回归(最小二乘法)
输入输出描述
输入:自变量X至少一项或以上的定量变量,因变量Y要求为定量变量(若为定类变量,请使用逻辑回归)。
输出:模型检验优度的结果,自变量对因变量的线性关系等等。
岭回归(Ridge)
详细解释
岭回归(Ridge)是一种针对小样本数据,处理自变量多重共线性问题(一般VIF值大于10)的一种有偏估计回归方法。岭回归通过引入一个正数改进正规方程组,提供一种有偏估计的方法消除共线影响。当K=0时,即为最小二乘估计,由于岭回归为有偏估计,K的取值应尽可能小。岭回归放弃了普通最小二乘法的无偏估计,损失了部分信息,因此岭回归方程的R²通常会稍低于普通最小二乘回归,但其估计的偏回归系数往往更接近真实的情况,从而提高了模型的稳定性和可靠性,对于病态数据的修复和拟合,具有较好的效果。 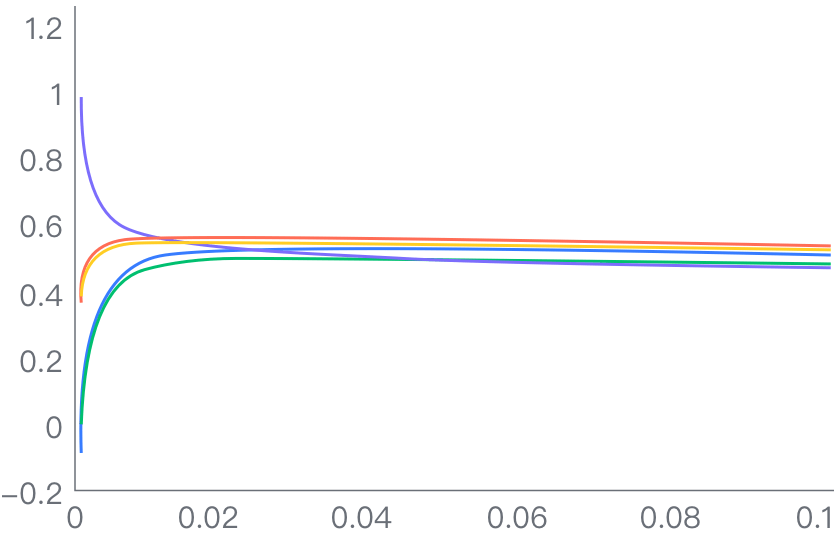
示例:
通过自变量(房子年龄、是否有电梯、楼
层高度、房间平方、房子单价)拟合预测
因变量(房价),现在发现房子单价与楼
层高度之间有着很强的共线性,VIF值高
于20;不能使用常见的最小二乘法OLS回
归分析,需要使用岭回归模型。
输入输出描述
输入:自变量X至少一项或以上的定量变量,因变量Y要求为定量变量(若为定类变量,请使用逻辑回归)。
输出:模型检验优度的结果,自变量对因变量的线性关系等等。
分层回归【检验某个变量是否是不可或缺的】
详细描述
分层回归(层次回归)本质上是建立在回归分析基础上,区别在于分层回归可分为多层,用于研究两个或者多个回归模型之间的差异。分层回归将核心研究的变量放在最后一步进入模型,以考察在排除了其他变量的贡献的情况下,该变量对回归方程的贡献。如果变量仍然有明显的贡献,那么就可以做出该变量确实具有其他变量所不能替代的独特作用的结论。这种方法主要用于,当自变量之间有较高的相关,其中一个自变量的独特贡献难以确定的情况。例如,在研究学习疲倦感中,将性别、年龄、学历等(控制变量)放置在第一层,第二层放置工作压力(核心研究变量)。常用于中介作用或者调节作用研究。 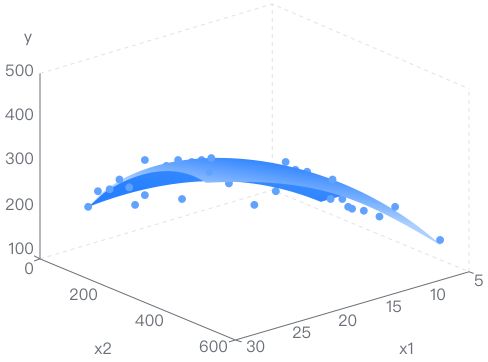 示例:
示例:
某高校随机抽取600名大学生,调查其身高、体重、
胸围、体育成绩和肺呼量(Y)数据,控制身高、体
重、体育成绩,分析胸围对肺呼量的影响程度。
输入输出描述
输入:多层次的线性回归数据。
输出:上一个层次与下一个层次的拟合变化情况,用于分析多加入的变量对自变量(Y)的影响程度。
灰色预测模型GM(1,1)【重点/含不确定因素的系统】
详细解释
灰色预测是一种对含有不确定因素的系统进行预测的方法。灰色预测通过鉴别系统因素之间发展趋势的相异程度,即进行关联分析,并对原始数据进行生成处理来寻找系统变动的规律,生成有较强规律性的数据序列,然后建立相应的微分方程模型,从而预测事物未来发展趋势的状况。 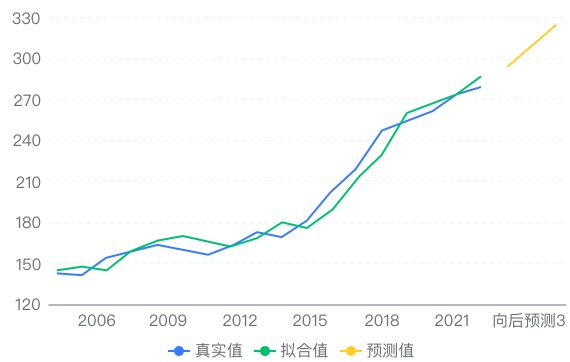 示例:
示例:
基于2000-2021年某产品的年销售
量,使用灰色预测模型对未来年销售
量进行预测。
输入输出描述
输入:1个时间序列定量变量。
输出:灰色预测的拟合预测结果。
聚类分析K-means【重点/常用】
详细解释
聚类分析是一种基于中心的聚类算法(K均值聚类),通过迭代,将样本分到K个类中,使得每个样本与其所属类的中心或均值的距离之和最小。与分层聚类等按照字段进行聚类的算法不同的是,快速聚类分析是按照样本进行聚类。 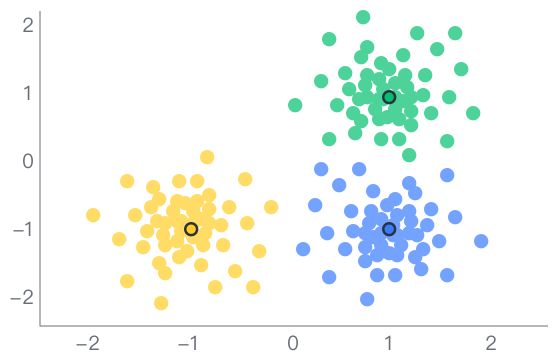 示例:
示例:
根据调研用户的收入、年龄、学历等变量
进行聚类,分为高质量人类,精英人士与
普通人3个类别。
输入输出描述
输入:1个或一个以上的定类变量(独热编码非必选)或者定量变量,预先设定类别个数。
输出:根据预先设定的类别个数,划分为其设定的类别。
逻辑回归【多定量自变量是否决定某个定类因变量】
详细解释
逻辑回归是研究二分类因变量与一些影响因素之间关系的一种多变量分析方法。但如果因变量是多个类别的,则要用到多分类逻辑回归去研究因变量与一些影响因素之间的关系。
输入输出描述
输入:因变量Y为分类变量,自变量X为至少一项定量变量。
输出:逻辑回归系数估计以及分类预测的效果评价。
Lasso回归【 一般用于处理自变量多重共线性问题 】
详细解释
Lasso方法是一种替代最小二乘法的压缩估计方法。Lasso的基本思想是建立一个L1正则化模型,在模型建立过程中会压缩一些系数和设定一些系数为零,当模型训练完成后,这些权值等于0的参数就可以舍去,从而使模型更为简单,并且有效防止模型过拟合。被广泛用于存在多重共线性数据的拟合和变量选择。 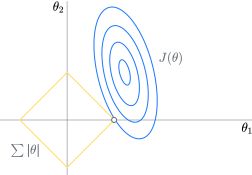 示例:
示例:
现对一批糖尿病患者进行分析,
分别获得了年龄、性别、体重指
数、平均⾎压等数据,现使用
Lasso回归分析⼀年后疾病进展
的测量值和重要影响变量。
输入输出描述
输入:自变量X至少一项或以上的定量变量或二分类定类变量,因变量Y要求为定量变量(若为定类变量,请使用逻辑回归)。
输出:模型检验优度的结果,自变量对因变量的线性关系和变量筛选结果等。
分层聚类【生成树状图关系时用】
详细解释
分层聚类法是一种常见的聚类算法。其基本思想是:先将待聚类的元素各自看成一类。然后,选择距离最小的两个类合并成一个新类,并计算出所得新类和其它各类的距离;接着再将距离最近的两类合并,直至将所有的样本都合并成一类为止。这种连续合并的过程可用树状图来表示,从而给出最终的聚类情况。 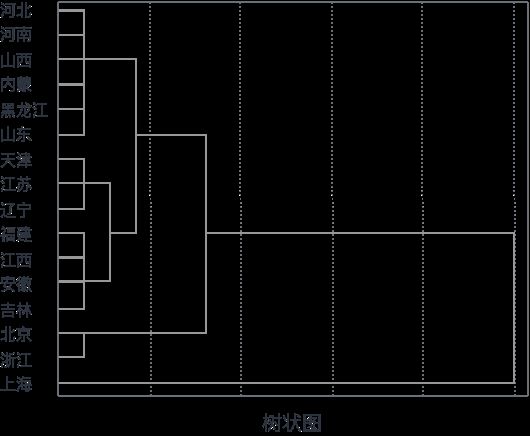 示例:
示例:
根据16个地区的每人平均生活消费支
出情况的六个指标,对这16个地区进
行分层聚类分析。
输入输出描述
输入:一个以上的定量变量和可选的索引项。
输出:个体或者变量被划分的类别和树状图(谱系图)。
有序逻辑回归【适用于因变量为等级或者程度差别的有序变量】
详细解释
有序逻辑回归适用于因变量为等级或者程度差别的有序变量,如因变量满意度分为不满意记为1,满意记为2,非常满意记为3。目的是为了研究有序分类因变量与一些影响因素之间的关系。
输入输出描述
输入:因变量Y为有序分类变量,自变量X至为少一项或以上的定量变量。
输出:有序逻辑回归系数估计以及分类预测的效果评价。
偏最小二乘回归(PLSR)【用一组变量去预测另一组变量】
详细解释
偏最小二乘回归(PLSR)是一种多对多线性回归建模的方法,用一组变量去预测另一组变量,常用于当两组变量(列)数很多,且都存在多重相关性,而观测数据的样本量(行)又较少时的情况。其原理是整合了主成分分析,典型相关分析和线性回归三种方法,在分析结果中,不仅可以提供一个的回归模型,也附带一些主成分分析和典型相关分析的内容。 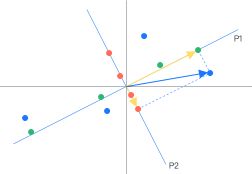 示例:
示例:
分析健身俱乐部的20位中年男子的体能数据。第一组是身体特征指标X,包括:体重、腰围、脉搏。第二组变量是训练结果指标Y,包括:单杠、弯曲、跳高。粗略分析发现数据量少且相关性较高,故使用偏最小二乘回归(PLSR)进行分析。
输入输出描述
输入:自变量Y至少一项或以上的定量变量,因变量X要求为至少两项或以上的定量变量。
输出:主成分分析和回归分析的结果等。
二分类概率单位回归(Probit)【二分类概率单位回归(Probit)以及分类预测的效果评价】
详细解释
概率单位回归(Probit)是一种与逻辑回归类似的定性回归模型,逻辑回归的系数约为概率单位回归的1.6倍。这是因为逻辑回归的连接函数为Logit累计概率函数,而概率单位回归(Probit)的连接函数为正态分布的累计概率函数,如果在概率单位回归过程选择Logit变换,即可得到逻辑回归模型。 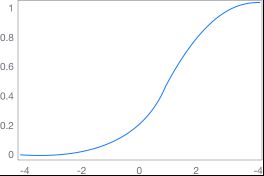 示例:
示例:
某公司需要调查员工流失的原
因,收集了约200名员工的工
作数据(员工满意度/月均工
作时长/薪资水平等),试分
析员工离职的原因并进行预测。
输入输出描述
输入:因变量Y为二分类定类变量,自变量X至为少一项或以上的定量变量。
输出:二分类概率单位回归(Probit)以及分类预测的效果评价。
Deming’s回归【自变量X可存在明显误差时替代最小二乘法】
详细解释
Deming’s 回归类似于普通最小二乘法的回归模型(OLS)。OLS法的前提条件较为严格,其认为自变量X应无明显误差,而Deming’s回归则无此前提,在系数估计上同时考虑了自变量X和因变量Y的残差波动。实际应用中,主要用于对方法的比较研究,也用作自变量和因变量均为随机数据的拟合和预测。
输入输出描述
输入:因变量Y、自变量X各为一个定量变量。
输出:Deming’s回归的方程以及部分检验结果。
统计建模
主成分分析(PCA)【用原始变量求出线性组合的目标函数】【重点】
详细解释
主成分分析将多个有一定相关性的指标进行线性组合,以最少的维度解释原数据中尽可能多的信息为目标进行降维,降维后的各变量间彼此线性无关,最终确定的新变量是原始变量的线性组合,且越往后主成分在方差中的比重也小,综合原信息的能力越弱,与因子分析不同的是,因子分析是利用少数几个公共因子去解释较多个要观测变量中存在的关系,它不是对原始变量的重新组合。 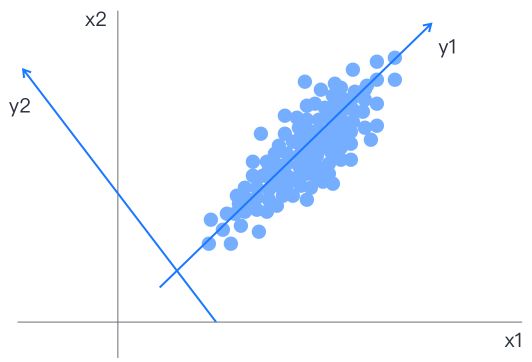
输入输出描述
输入:2个或两个以上的定量变量(假设为N个变量)。
输出:最低可降维成1维(一个变量,一般用于综合评价),最多可降维成N个变量(一般用于数据脱敏),同时可以获取降维后各个变量的组成权重,用于代表原先变量的数据保留情况。
典型相关分析
详细解释
典型相关分析是研究多个变量和多个变量之间的线性相关关系,能够揭示出两组变量之间的内在联系。首先在每组变量中找到变量的线性组合,使得两组的线性组合之间具有最大的相关系数。然后选取和最初挑选的这对线性组合不相关的线性组合,使其配对,并选取相关系数最大的那一组。如此继续配对,直到两组变量之间的相关性被提取完。 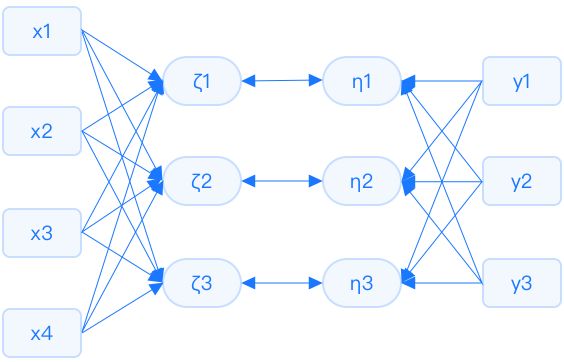 示例:
示例:
研究200名大学生四个学术得分变量
与三个心理得分变量之间的关系。
输入输出描述
输入:集合Y为至少两项或以上的定量变量或有序定类变量,集合Y为至少两项或以上的定量变量或有序定类变量。
输出:成对典型变量的相关性,以及典型变量对研究变量的解释比例。
泊松分布检验【 检验某种事件是否发生概率很低,但一定会发生,且很稳定 】
详细解释
泊松分布描述的是一个小概率事件在单位时间内发生的次数,如每个小时进入银行办理业务的人数、报纸上每一页的错别字数量、某个网页的点击量等,简单地说,就是泊松检验的是某种事件是否发生概率很低,且很稳定,同时发生频数的大小之间没有影响关系,例如在一定时间内产品产生的用户需求数,上周发生的用户提的需求数跟这周的没关系。
输入输出描述
输入:一个定量变量。
输出:是否呈现泊松分布。
游程检验【 检验一件事情发生的概率是否为随机的 】
逐步回归【在回归分析的基础上,通过剔除不太重要的变量来进行变量的筛选】
线性判别(LDA)【常用于数据降维,可在数据处理的降维部分使用】
详细解释
线性判别的原理是将样本投影到一条直线上,使得同类样本的投影点尽可能接近,不同样本的投影点尽可能远离;在对新样本进行分类时,将其投影到同样的直线上,再根据投影点的位置来确定新样本的类别。其中线性判别(LDA)也常用于数据降维,可在数据处理的降维部分使用。 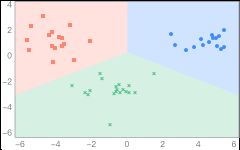 示例:
示例:
根据红酒的颜色强度,脯氨酸,
类黄酮等变量,生成一个能够区
分琴酒,雪莉,贝尔摩德三种品
种的红酒的线性判别模型。
输入输出描述
输入:自变量X为1个或1个以上的定量变量,因变量Y为一个定类变量。
输出:模型的分类结果和模型分类的评价效果。
极差分析【 通过比较极差大小来分析数据的方法,主要用于正交试验的数据分析 】
拟合工具箱【工具】
详细解释
拟合工具箱适用于对二维、三维数据的进行线性、非线性拟合。
输入输出描述
输入:因变量为一个定量变量;自变量为不超过2个的定量变量。
输出:拟合效果以及可视化拟合情况。
机器学习分类
决策树分类
详细解释
决策树中每个内部节点都是一个分裂问题:指定了对实例的某个属性的测试,它将到达该节点的样本按照某个特定的属性进行分割,并且该节点的每一个后继分支对应于该属性的一个可能值。分类决策树叶节点所含样本中,其输出变量的众数就是分类结果。 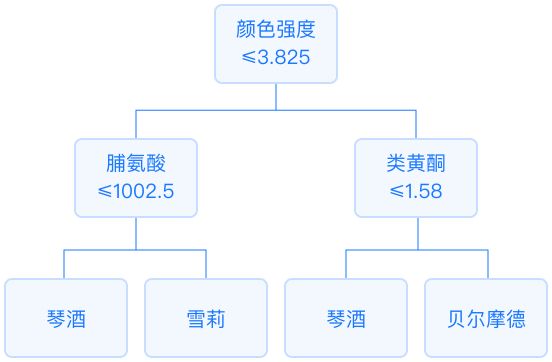 示例:
示例:
根据红酒的颜色强度,脯
氨酸,类黄酮等变量,生
成一个能够区分琴酒,雪
莉,贝尔摩德三种品种的
红酒的决策树。
输入输出描述
输入:自变量X为1个或1个以上的定量变量,因变量Y为一个定类变量。
输出:模型输出的决策树结构图及模型的分类效果。
随机森林分类【 多棵决策树组合在一起的多数投票结果 】
详细解释
随机森林分类在生成众多决策树的过程中,是通过对建模数据集的样本观测和特征变量分别进行随机抽样,每次抽样结果均为一棵树,且每棵树都会生成符合自身属性的规则和分类结果,而森林最终集成所有决策树的规则和分类结果,实现随机森林算法的分类。 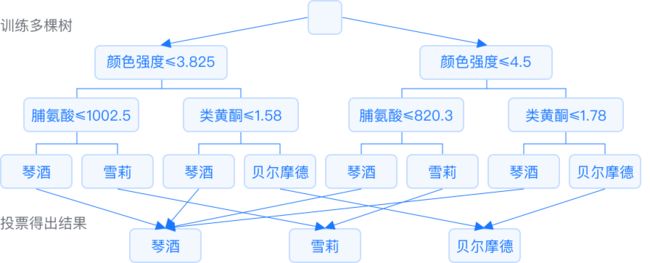 示例:
示例:
根据红酒的颜色强度,脯
氨酸,类黄酮等变量,生
成一个能够区分琴酒,雪
莉,贝尔摩德三种品种的
红酒的随机森林。
输入输出描述
输入:自变量X为1个或1个以上的定量变量,因变量Y为一个定类变量。
输出:模型的分类结果和模型的分类评价情况。
K近邻分类(KNN)【 判断新样本类别的一种有监督算法 】
详细解释
K近邻(KNN)分类器是有监督学习中普遍使用的分类器之一,将观察值的分类判定为离它最近的k个观察值中所占比例最大的分类。 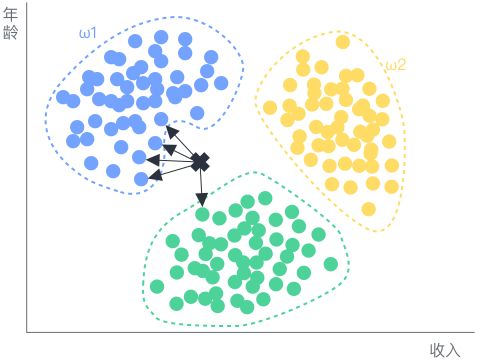 示例:
示例:
根据高质量人类,精英
人士与普通人3个类别的
收入、年龄训练一个
KNN分类器,用于对一
个新用户进行分类。
输入输出描述
输入:自变量X为1个或1个以上的定量变量,因变量Y为一个定类变量。
输出:模型的分类结果和模型分类的评价效果。
BP神经网络分类【MLP】
详细解释
bp神经网络是一种按误差逆传播算法训练的多层前馈网络,是目前应用最广泛的神经网络模型之一。bp神经网络的学习规则是使用最速下降法,通过反向传播来不断调整网络的权值和阈值,使网络的分类错误率最小。 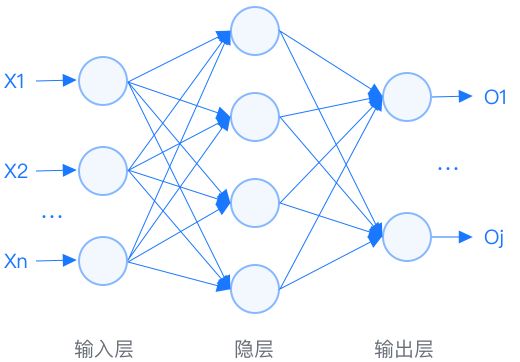 示例:
示例:
有一批Iris花,已知这批Iris花可
分为3个品种,现需要对其进行
分类。根据花萼长度、花萼宽
度、花瓣长度、花瓣宽度的数
据。用已有的数据训练一个神
经网络用作分类器。
输入输出描述
输入:自变量X为1个或1个以上的定量变量,因变量Y为一个定类变量。
输出:模型的分类结果和模型分类的评价效果。
支持向量机(SVM)分类【有监督学习二分类】
详细解释
支持向量机(SVM)是一类按监督学习方式对数据进行二元分类的广义线性分类器,其决策边界是对学习样本求解的最大边距超平面。 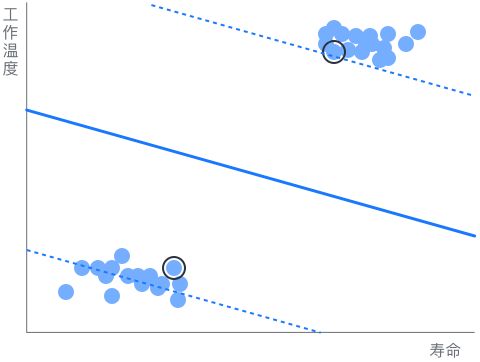 示例:
示例:
根据2种产品的最低工作温
度和最长寿命(年),生成一
个可以区分这两种产品的
支持向量机(SVM)分类器。
输入输出描述
输入:自变量X为1个或1个以上的定量变量,因变量Y为一个定类变量。
输出:模型的分类结果和模型分类的评价效果。
朴素贝叶斯分类【 假设特征之间独立的条件下以贝叶斯为基础的简单概率分类器 】
详细解释
朴素贝叶斯分类器(Naive Bayes classifier),在机器学习中是一系列以假设特征之间强(朴素)独立下运用贝叶斯定理为基础的简单概率分类器。 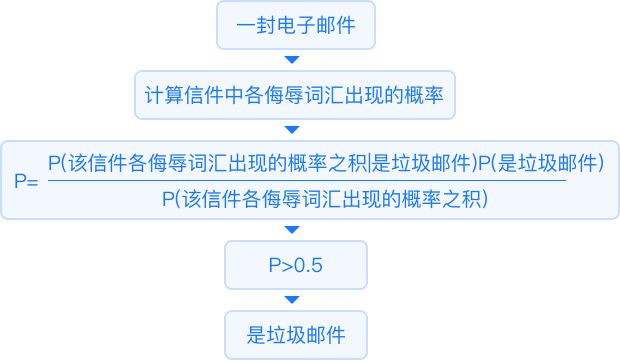 示例:
示例:
根据一封邮件的内容,
用一个朴素贝叶斯分类
器,计算这封邮件是否
属于垃圾邮件。
输入输出描述
输入:自变量X为1个或1个以上的定量变量,因变量Y为一个定类变量。
输出:模型的分类结果和模型分类的评价效果。
逻辑回归(梯度下降法)【多分类非决策问题,BP神经网络不会用时考虑】
详细解释
逻辑回归,是一种名为“回归”的线性分类器,其本质是由线性回归变化而来的,一种广泛使用于分类问题中的广义回归算法。  示例:
示例:
以肺炎病情分析为例,选择两组人群,
一组是肺炎组,一组是非肺炎组,两组
人群必定有不同的体征与生活方式(自
变量),比如年龄、性别、饮食习惯、
是否吸烟等,因变量就是是否得肺炎,
值为”是“或”否“。
输入输出描述
输入:自变量X为1个或1个以上的定量变量,因变量Y为一个定类变量。
输出:模型的分类结果和模型分类的评价效果。
机器学习回归【可以和预测模型中的算法对比,取更优者,原理基于机器学习分类中的基础算法】
规划自动求解器【工具】【重点】
系统将根据输入的目标函数,约束条件和未知数取值范围自动判断其规划类型然后提示可用的求解方法。
最优解问题——线性规划
内点法
单纯形法
修正单纯形法
最优解问题——非线性规划
下山单纯形法
改进BFGS拟牛顿法
改进共轭方向法
(边界)截断牛顿法
线性近似束优化法
序贯最小二乘规划算法
信赖域算法
整数规划
分支定界法
0-1规划
枚举法
启发式算法【重点】
遗传算法(GA)【重点】
详细解释
模拟物竞天择的生物进化过程,通过维护一个潜在解的群体执行了多方向的搜索,并支持这些方向上的信息构成和交换。  示例:
示例:
通过遗传算法对非线性规划问题进行求解。
输入输出描述
输入:目标函数,约束条件和未知数。
输出:规划求解结果,以及规划求解方程导出。
粒子群算法(PSO)
详细解释
将每个解看作搜索空间中的一个粒子。每个粒子都有一定的速度,其大小根据自身历史经验和种群经验进行动态调整,通过不断地迭代飞行来寻找空间中最优解的位置。
输入输出描述
输入:目标函数,约束条件和未知数。
输出:规划求解结果,以及规划求解方程导出。
模拟退火算法(SA)【重点】【寻找全局最优解】
详细解释
其出发点是基于物理中固体物质的退火过程与一般组合优化问题之间的相似性。从某一较高初温出发,伴随温度参数的不断下降,结合概率突跳特性在解空间中随机寻找目标函数的全局最优解。
输入输出描述
输入:目标函数,约束条件和未知数。
输出:规划求解结果,以及规划求解方程导出。
蒙特卡洛算法【不建议】
详细解释
是一种使用随机数来解决规划问题的方法,其精确度很大程度取决于实验次数。
输入输出描述
输入:目标函数,约束条件和未知数。
输出:规划求解结果,以及规划求解方程导出。