非递归后序遍历二叉树总结

---

前言

关于之前写的非递归遍历二叉树的一份代码由于当时图省事几乎没有注释，导致今天再次看代码时比较费劲。这份代码是纯C写的，设计到许多栈、指针的操作，可读性不高，于是现在通过这份博客对于非递归后序遍历二叉树进行一个总结回顾。以及完善当时的部分注释。文章链戳这里

---

正文

进入正题，关于遍历二叉树常用的方法是递归遍历。优点是代码量小，逻辑精炼，可读性高。而对于递归实际上在底层的汇编代码中，是开辟了一个系统栈，不断进行保护现场、恢复现场的操作。但显而易见的是，系统栈存在一定的限制，有个别极端的情况会出现爆栈的问题，于是引入非递归遍历，通过利用手写的栈来保存每次遍历的结点信息来完成二叉树的遍历。
对于非递归先序和中序遍历二叉树代码逻辑很类似，每次访问到一个非空结点就压栈，唯一区别的是访问该节点信息的顺序，关于这两个在这就不一一叙述。接下来描述非递归后序遍历二叉树：
在此之前，我们要先介绍一下后序遍历的线索二叉树存在着的不足，如图

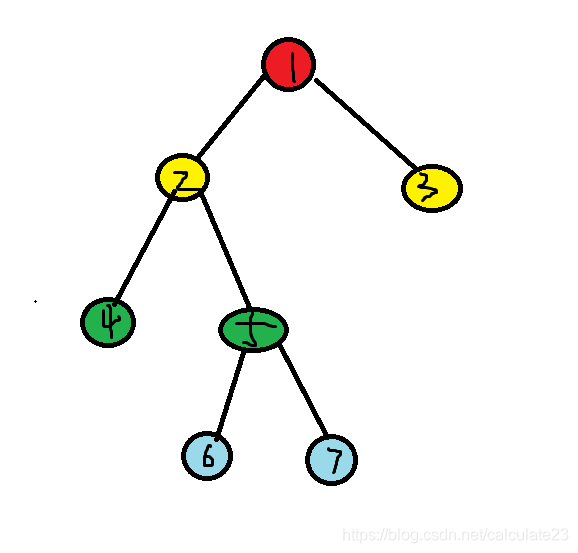
后序遍历的线索二叉树不能解决求后序后继的问题，比如结点5，它的后继显然是2，然而它右孩子却没有空的指针域来存放这个后继。
关于为什么说这个问题个人感觉和后序遍历二叉树时访问一个子树根结点的顺序有关。
下面描述关于见到二叉树某个结点的操作周期：

• 首次得到结点V（非空）时肯定是双亲结点要访问左子树，此时它显然不是终点（因为终点是空），于是我们将它压入栈中，等待下一次访问
• 第二次访问时一定是左子树操作完毕后回溯到它，此时还不能将它弹出栈，因为还有右子树没访问
• 第三次访问是从右子树操作完毕后回来，显然此时要询问它的结点信息，然后弹出栈，回到它的双亲结点

综上，我们在关键步骤是考虑某个结点的询问方向：如果是从双亲结点过来，就要将该点压栈；如果是从左孩子过来就要转去访问它的右孩子；如果是从右孩子过来就要访问它的结点信息，然后弹出栈。

---

代码实现

思路一

我们每次跟栈顶结点进行比较，让栈顶元素一直是当前元素的一个父节点；
维护一个flag标志表示此时是从哪里回到该节点，首先先压入根结点，然后左转进入迭代。如果当前结点cur非空且flag=1，说明是第一次访问，压栈，左转；否则判断是否为栈顶元素的左结点，是则右转；否则出栈并访问结点信息。关键的一步是进入一个循环，让当前结点成为栈顶元素的左孩子，不是的话直接出栈并访问结点信息。
Code：

Status PostOrderTraverse(BiTreePoint T)
{
	BiTreePoint *temp;
	Status flag=1;
	StackHeadPoint Head=InitStack();
	if(T==NULL || !StackPush(&Head,&T)) //根节点入栈
	{
		printf("\n");
		return OK;
	}
	temp=&T->lchild; //左转，构造成当前元素是栈顶元素的左孩子的一个状态
	while(!StackEmpty(Head))
	{
		if(*temp && flag) //第一次访问，压栈左转
		{
  			if(!StackPush(&Head,temp))
			{
				printf("对不起,当前系统内存不足,二叉树遍历失败!\n");
				return NO;
			}
			temp=&(*temp)->lchild;
		}
		else if(temp==&(*(getTop(&Head)))->lchild) //第二次访问，右转
		{
			temp=&(*(getTop(&Head)))->rchild;
			flag=1;
		}
		else //第二次访问，出栈询问，并保持成当前节点是栈顶元素的左孩子的状态
		{
			temp=getTop(&Head);
			StackPop(&Head);
			printf("%c",(*temp)->data);
			while(temp!=&T && temp==&(*(getTop(&Head)))->rchild) //右孩子显然要访问当前结点信息然后回溯上去
			{
				temp=getTop(&Head);
				StackPop(&Head);
				printf("%c",(*temp)->data);
			}
			flag=0;
		}
	}
	StackDelete(&Head);
	printf("\n");
	return OK;
}

思路二

利用栈的特性(FILO)，我们要构造的访问序列可以概述为LRN，对于每个结点的子节点我们入栈的顺序可以是NRL，出栈的时候就可以构造成LRN的效果了，这其实利用到的原理是先序遍历序列和后序遍历序列可以确定两个结点的父子关系，反过来的先序入栈其实就是后序遍历的效果。对于具体实现我们先把root入栈，然后每次发现一个叶子节点或者发现某个结点从孩子结点传递回来，显然就可以输出，为什么？因为根据入栈的顺序出栈时一旦发现前一个结点是当前栈顶的右孩子时，左孩子显然已经出栈完毕，不存在说左孩子还没打印就打印右孩子的情况。其实根据这个逻辑通俗地讲就是：有叶子节点马上打印，否则判断当前结点是不是上次打印的祖先，是的话也就打印（不是的话其实就是做一次性把左右子树的根都入栈的操作），特别地对于根节点最后一次打印，所以第一次维护的before指针要设置为NULL来区别根节点和其他子树根节点
Code：

Status PostOrderTraverse2(BiTreePoint T)
	BiTreePoint *temp,*before;
	StackHeadPoint Head=InitStack();
	if(T==NULL || !StackPush(&Head,&T))
	{
		printf("\n");
		return OK;
	}
	before=NULL;
	while(!StackEmpty(Head))
	{
		temp=getTop(&Head);
		if( (*temp)->lchild==NULL && (*temp)->rchild==NULL || before && (before==&(*temp)->lchild || before==&(*temp)->rchild) )
		{
			printf("%c",(*temp)->data);
			StackPop(&Head);
			before=temp;
		}
		else
		{ //注意这里面是反序入栈RL，达到出栈时LR的顺序
			if((*temp)->rchild)
			{
				if(!StackPush(&Head,&(*temp)->rchild))
				{
					printf("对不起,当前系统内存不足,二叉树遍历失败!\n");
					return NO;
				}
			}
			if((*temp)->lchild)
			{
				if(!StackPush(&Head,&(*temp)->lchild))
				{
					printf("对不起,当前系统内存不足,二叉树遍历失败!\n");
					return NO;
				}
			}
		}
	}
	StackDelete(&Head);
	printf("\n");
	return OK;
}

思路三

这是王道上面的算法参考答案，逻辑比上面两个都简明一点，但其实和思路一很类似，只不过它实现起来没有那么冗长。就是借助一个r指针来存放上一次访问的指针，每次栈顶元素跟其比较一下到底是左孩子上来的还是右孩子上来的。区别的是，每当一子树遍历完毕后将当前指针置为空，下一次直接转右子树或者输出子树的根节点
总之，就是每次往左走走到最底打印结点后能右转左拐就右转左拐，否则打印这个子树的祖先结点后结束这边的搜索分支回溯上去
Code：

void PostOrder(BiTree T) {
	InitStack(S);
	p = T;
	r = NULL;
	while (p || !IsEmpty(S)) {
		if (p) { //不到达终点继续往左转
			push(S, p);
			p = p->lchild;
		} else {//否则向右
			GetTop(S, p); //取栈顶元素
			if (p->rchild && r != p->rchild) { //右子树存在且未被访问则右转马上左转
				p = p->rchild;
				push(S, p);
				p = p->lchild;
			} else {
				pop(S, p);
				vist(p->data);
				r = p; //记录上一个访问的结点
				p = NULL;//很重要  走到这里相当于某个子树完全搜索完毕，下一次一定要再取个栈顶元素，并且考虑要不要右转
			}
		}
	}
}

思路四

发现这几个非递归的结点绝大多数都和子树根节点是否访问有关，我们可以在每个域中增加一个是否访问过的标志位来判断结点分支是否被遍历过。

---

总结

除了思路二，我们发现在栈中的结点必然是当前结点的祖先，从栈顶到栈底的结点和p恰好构成一条树上的路径。比如某个祖先结点到其子孙结点的路径就可以根据后序遍历的特性来求得。LCA问题实际上也是利用这个后序遍历的特性来完成的，比如Tarjan算法是先把子孙结点合并后在合并到当前结点，结合上并查集后就可以离线处理LCA(T, u, v)的询问了。

回到顶部