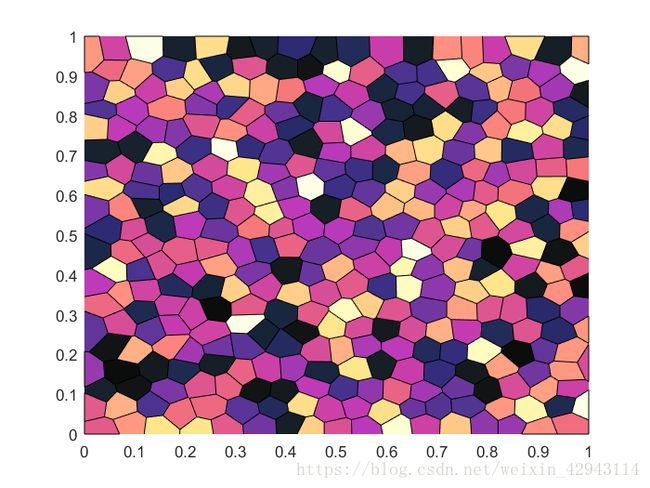
泰森多边形（Voronoi彩图）的matlab绘制——2

泰森多边形（Voronoi图）的matlab绘制——彩图版

1 Voronoi图简介

泰森多边形是对空间平面的一种剖分，其特点是多边形内的任何位置离该多边形的样点（如居民点）的距离最近，离相邻多边形内样点的距离远，且每个多边形内含且仅包含一个样点。由于泰森多边形在空间剖分上的等分性特征，因此可用于解决最近点、最小封闭圆等问题，以及许多空间分析问题，如邻接、接近度和可达性分析等。

泰森多边形的构建可以分为2个步骤，1是Delaunay三角网的构建，2是三角网格外接圆心得连线。

之前我有写过一篇文章，主要是泰森多边形的边缘绘制。内边的思路是根据每一个三角形的Delaunay三角网关系，去依次连接每个相邻三角形外接圆心得到。外边的思路是根据每个外接圆圆心和相应边缘做中垂线得到的。
参见：
泰森多边形（Voronoi图）的matlab绘制 https://blog.csdn.net/weixin_42943114/article/details/82319332

二维Delaunay三角网的绘制参见 https://blog.csdn.net/weixin_42943114/article/details/82262122

2 实心带色彩的Voronoi图实现思路

实心带色彩的Voronoi图主要是通过matlab里的patch()函数实现的。
具体用法可以参见matlab的官方帮助：https://ww2.mathworks.cn/help/matlab/ref/patch.html

其中本文最主要的用法是

patch('Faces',f,'Vertices',v,'FaceVertexCData',col,'FaceColor','flat');

v是一系列点矩阵，f是多边形对应的点的编号，col是多边形的颜色，取[0,1]。

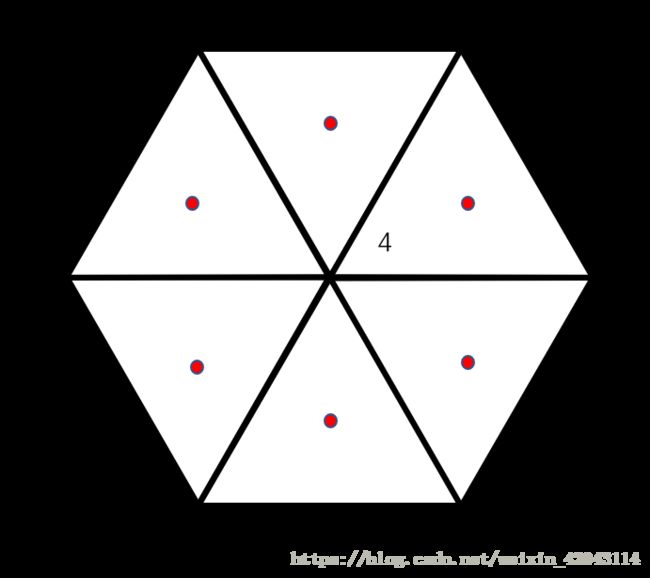
根据前两篇文章里的算法，已知所有的初始点xdot，和已经构建关系的三角形网格。之后循环每一个初始点，依次连接点初始点周围三角形的外接圆心即可。

比如对于以下图形：

以点4为例，和点4相关的三角形依次为

[4,3,1;
4,1,2;
4,2,5;
4,5,7;
4,7,6;
4,6,3;]

这些三角形，他们的外接圆圆心为红点所示。所以点4所对应的泰森多边形为这些红色点依次相连的对应的多边形：

如果遇到边缘三角形，思路和上一篇文章相同，都是做边缘的延长线。和上一篇文章中惟一的不同就是，上一篇文章只需要得到线即可，所以延长线画到很远处就行；但是这里要求得到面，所以需要求延长线与边界的交点。这里做的是边缘延长线与边界的交点作为泰森多边形的一个顶点。

3 matlab代码以及得到的结果图

3.1 matlab自带的代码

%采用matlab自带的函数进行绘制
clear
xdot=gallery('uniformdata',[200 2],5);
%delaunay三角形
figure(1)
DT=delaunayTriangulation(xdot);
triplot(DT,'color','k')
%voronoi三角形
figure(2)
voronoi(xdot(:,1),xdot(:,2));
xlim([0,1])
ylim([0,1])
%绘制voronoi三角形彩色
figure(3)
[v,c]=voronoin(xdot); %不是voronoi是voronoin
xlim([0,1])
ylim([0,1])
for i = 1:length(c) 
    patch(v(c{i},1),v(c{i},2),rand(1,1));
end

3.2 自编程实现代码

因为涉及到了之前的两篇文章的内容，所以代码看起来非常的冗长。其实这篇代码完全可以采用外部函数调用的方式做到很整洁，只需要多创立几个m文件把这段代码拆分即可。

%更改了3里面几个bug，
%1.结果要输出最终面的形式，添加Txdot
clear

%0 设置初始点模块*********************************************************************************
N=400;
%点随机

xdot=rand(N,2);
%点按圆形随机
% r=rand(N,1).^0.3;
% theta=rand(N,1)*2*pi;
% xdot=[r.*cos(theta)/2+0.5,r.*sin(theta)/2+0.5];
%点按双行随机
% x=rand(N,1);
% y=[randn(N/2,1)/5+0.5;randn(N/2,1)/5-0.5];
% y(y>1)=1;y(y<-1)=-1;
% y=(y+1)/2.1;
% xdot=[x,y];

%点按规则矩形加抖动
% [X1,X2]=meshgrid(0:1/sqrt(N):1-1/sqrt(N));
% xdot=zeros(N,2);
% xdot(:,1)=X1(1:end)'+1/sqrt(N)/2*rand(N,1);
% xdot(:,2)=X2(1:end)'+1/sqrt(N)/2*rand(N,1);

%点按随机三角加抖动
% NN=20;
% X1=[];X2=[];
% for j=1:NN
%      if mod(j,2)==0
%          X1=[X1;(0:1/NN/sqrt(3)*2:1-0/NN/sqrt(3)*2)'];
%          X2=[X2;ones(length(0:1/NN/sqrt(3)*2:1-0/NN/sqrt(3)*2),1)*(j-1)/NN];
%      else
%          X1=[X1;(0:1/NN/sqrt(3)*2:1-1/NN/sqrt(3)*2)'+1/NN/sqrt(3)];
%          X2=[X2;ones(length(0:1/NN/sqrt(3)*2:1-1/NN/sqrt(3)*2),1)*(j-1)/NN];
%      end
% end
% N=size(X1,1);
% xdot=[X1+rand(N,1)*1.2/NN/sqrt(3),X2+rand(N,1)*1.2/NN/2];
%点按圆形螺旋
r=0:1/500:1;
r=r.^0.7;
theta=0:0.1:500*0.1;
theta=theta.^1.3;
xdot=[(r.*cos(theta))'/2+0.5,(r.*sin(theta))'/2+0.5];
N=size(xdot,1);

%1 Delaulay三角形的构建*******************************************************************************

%整理点，遵循从左到右，从上到下的顺序
xdot=sortrows(xdot,[1 2]);

%画出最大包含的三角形
xmin=min(xdot(:,1));xmax=max(xdot(:,1));
ymin=min(xdot(:,2));ymax=max(xdot(:,2));
bigtri=[(xmin+xmax)/2-(xmax-xmin)*1.5,ymin-(xmax-xmin)*0.5;...
    (xmin+xmax)/2,ymax+(ymax-ymin)+(xmax-xmin)*0.5;...
   (xmin+xmax)/2+(xmax-xmin)*1.5,ymin-(xmax-xmin)*0.5];

xdot=[bigtri;xdot];%点集
edgemat=[1 2 xdot(1,:) xdot(2,:);...
    2 3 xdot(2,:) xdot(3,:);1 3 xdot(1,:) xdot(3,:)];%边集，每个点包含2个点，4个坐标值
trimat=[1 2 3];%三角集,每个三角包含3个点
temp_trimat=[1 2 3];
for j=4:N+3
    pointtemp=xdot(j,:);%循环每一个点
    deltemp=[];%初始化删除temp_trimat的点
    temp_edgemat=[];%初始化临时边
    for k=1:size(temp_trimat,1)%循环每一个temp_trimat的三角形
        panduan=whereispoint(xdot(temp_trimat(k,1),:),...
            xdot(temp_trimat(k,2),:),xdot(temp_trimat(k,3),:),pointtemp);%判断点在圆内0、圆外1、圆右侧2
        switch panduan
            case 0
                %点在圆内
                %则该三角形不为Delaunay三角形
                temp_edge=maketempedge(temp_trimat(k,1),temp_trimat(k,2),temp_trimat(k,3),j,xdot);%把三条边暂时存放于临时边矩阵
                temp_edgemat=[temp_edgemat;temp_edge];
                deltemp=[deltemp,k];
                ;
            case 1
                %点在圆外，pass
                ;
            case 2
                %点在圆右
                %则该三角形为Delaunay三角形，保存到triangles
                trimat=[trimat;temp_trimat(k,:)];%添加到正式三角形中
                deltemp=[deltemp,k];
                %并在temp里去除掉
                %别忘了把正式的边也添加进去
                edgemat=[edgemat;makeedge(temp_trimat(k,1),temp_trimat(k,2),temp_trimat(k,3),xdot)];%遵循12,13,23的顺序
                edgemat=unique(edgemat,'stable','rows');
                
        end
%     clf
%     hold on
%     plot(xdot(:,1),xdot(:,2),'ko')
%     plot(pointtemp(:,1),pointtemp(:,2),'bo')
%     for h=1:size(edgemat,1)
%         plot([edgemat(h,3),edgemat(h,5)],[edgemat(h,4),edgemat(h,6)],'k-')
%     end
%     plot([xdot(temp_trimat(k,1),1),xdot(temp_trimat(k,2),1),xdot(temp_trimat(k,3),1),xdot(temp_trimat(k,1),1)],...
%         [xdot(temp_trimat(k,1),2),xdot(temp_trimat(k,2),2),xdot(temp_trimat(k,3),2),xdot(temp_trimat(k,1),2)],'r-')
%     
% 
%     hold off
    
    %三角循环结束    
    end
    
    
    
    %除去上述步骤中的临时三角形
    temp_trimat(deltemp,:)=[];
    temp_trimat(~all(temp_trimat,2),:)=[];
    %对temp_edgemat去重复
    temp_edgemat=unique(temp_edgemat,'stable','rows');
    %将edge buffer中的边与当前的点进行组合成若干三角形并保存至temp triangles中
    temp_trimat=[temp_trimat;maketemptri(temp_edgemat,xdot,j)];
    k=k;


%点循环结束
end

%合并temptri
trimat=[trimat;temp_trimat];
edgemat=[edgemat;temp_edgemat];
%删除大三角形
deltemp=[];
for j=1:size(trimat,1)
    if ismember(1,trimat(j,:))||ismember(2,trimat(j,:))||ismember(3,trimat(j,:))
        deltemp=[deltemp,j];
    end
end
trimat(deltemp,:)=[];
edgemat=[trimat(:,[1,2]);trimat(:,[2,3]);trimat(:,[3,1])];
edgemat=sort(edgemat,2);
edgemat=unique(edgemat,'stable','rows');


temp_edgemat=[];
temp_trimat=[];

% figure(1)
% hold on
% % plot(xdot(:,1),xdot(:,2),'ko')
% for j=1:size(trimat,1)
%     plot([xdot(trimat(j,1),1),xdot(trimat(j,2),1)],[xdot(trimat(j,1),2),xdot(trimat(j,2),2)],'k-')
%     plot([xdot(trimat(j,1),1),xdot(trimat(j,3),1)],[xdot(trimat(j,1),2),xdot(trimat(j,3),2)],'k-')
%     plot([xdot(trimat(j,3),1),xdot(trimat(j,2),1)],[xdot(trimat(j,3),2),xdot(trimat(j,2),2)],'k-')
% end
% hold off
% xlim([0,1]);ylim([0,1]);

%1.5 凸包监测****************************************************************************************
%思路是先找出边缘点（三角形只有1个或2个的），顺便整出一个三角形相互关系图，以后用。
%然后顺时针，依次隔一个点连接出一条线段，如果这个和之前的线段相交，则不算；如果不交，则记录出三角形
%更新完了以后，再监测一遍，直到没有新的为止。

t_w=0;
while t_w==0
    [~,border_point,~]=makebordertri(trimat);
    border_point=[border_point;border_point(1,:)];
    temp_edgemat=[];
    temp_trimat=[];
    for j=1:size(border_point,1)-1
        tempboderedge=[border_point(j,1),border_point(j+1,2)];
        tempboderdot=border_point(j,2);
        %寻找带tempboderdot的所有边
        tempdotex=edgemat(logical(sum(edgemat==tempboderdot,2)),:);
        %删除相邻边
        tempdotex(ismember(tempdotex,[tempboderdot,tempboderedge(1)],'rows'),:)=[];
        tempdotex(ismember(tempdotex,[tempboderedge(1),tempboderdot],'rows'),:)=[];
        tempdotex(ismember(tempdotex,[tempboderdot,tempboderedge(2)],'rows'),:)=[];
        tempdotex(ismember(tempdotex,[tempboderedge(2),tempboderdot],'rows'),:)=[];
        %检测tempdotex是否为空，如果是证明不用相连
        t_N=size(tempdotex,1);
        t_t=0;
        if t_N>0
            %依次检测是否相交，只要有一个相交就不算；如果都不想交，则相连
            for k=1:t_N
                if tempdotex(k,1)==tempboderdot
                    t_xdotno4=tempdotex(k,2);
                else
                    t_xdotno4=tempdotex(k,1);
                end
                tt_xdotno4=xdot(t_xdotno4,:)-xdot(tempboderdot,:);
                xdotno4=xdot(tempboderdot,:)+tt_xdotno4/sqrt(sum(tt_xdotno4.^2))*(sqrt((xmax-xmin)^2+(ymax-ymin)^2));
                panduan=crossornot(xdot(tempboderedge(1),:),xdot(tempboderedge(2),:),xdot(tempboderdot,:),xdotno4);
                if panduan==1
                    t_t=t_t+1;
                    break
                end
            end
            %t_t大于0说明有相交的线,略过
            if t_t==0
                temp_edgemat=[temp_edgemat;tempboderedge];
                temp_trimat=[temp_trimat;[tempboderedge,tempboderdot]];
                break
            end
        end
    end
    trimat=[trimat;temp_trimat];
    edgemat=[edgemat;temp_edgemat];
    %删除重复的三角形
    trimat=sort(trimat,2);
    trimat=unique(trimat,'stable','rows');
    if j==size(border_point,1)-1
        t_w=1;
    end
end


figure(2)
hold on
% plot(xdot(:,1),xdot(:,2),'ko')
for j=1:size(trimat,1)
    plot([xdot(trimat(j,1),1),xdot(trimat(j,2),1)],[xdot(trimat(j,1),2),xdot(trimat(j,2),2)],'k-')
    plot([xdot(trimat(j,1),1),xdot(trimat(j,3),1)],[xdot(trimat(j,1),2),xdot(trimat(j,3),2)],'k-')
    plot([xdot(trimat(j,3),1),xdot(trimat(j,2),1)],[xdot(trimat(j,3),2),xdot(trimat(j,2),2)],'k-')
end
hold off
xlim([0,1]);ylim([0,1]);

%2 泰森多边形的建立步骤 ******************************************************************************
%求每个三角形的外接圆圆心

trimatcenter=zeros(size(trimat,1),2);
for j=1:size(trimat,1)
    [a,b,~]=maketricenter(xdot(trimat(j,1),:),xdot(trimat(j,2),:),xdot(trimat(j,3),:));
    trimatcenter(j,:)=[a,b];
end
hold on
scatter(trimatcenter(:,1),trimatcenter(:,2),5,[0.6,0,0],'filled')
hold off

%求三角形的相邻三角形个数
[border_trimat,border_point,trimat_con]=makebordertri(trimat);
Thi_edge1=[];
for j=1:size(trimat,1)
    tempedge=[];
    %第一个相邻三角形
    if trimat_con(j,1)~=0
        tempedge=[tempedge;[j,trimat_con(j,1)]];
    end
    %第二个相邻三角形
    if trimat_con(j,2)~=0
        tempedge=[tempedge;[j,trimat_con(j,2)]];
    end
    %第三个相邻三角形
    if trimat_con(j,3)~=0
        tempedge=[tempedge;[j,trimat_con(j,3)]];
    end
    Thi_edge1=[Thi_edge1;tempedge];
end

%绘制非边缘泰勒多边形
figure(3)
Thi_edge1=unique(Thi_edge1,'stable','rows');
xlim([0,1]);ylim([0,1]);
hold on
for j=1:size(Thi_edge1,1)
    plot(trimatcenter([Thi_edge1(j,1),Thi_edge1(j,2)],1),trimatcenter([Thi_edge1(j,1),Thi_edge1(j,2)],2),'color',[0,0.4,0])
end



%绘制边缘泰勒多边形
%先逐个边试探，如果中心点在三角内，则做中心-边缘延长线
%如果中心点在三角外，如果在屏幕外，忽略，如果在屏幕内，做边缘-中心延长线

for j=1:size(border_point,1)
    %先找到边对应的三角
    temp_trimat=border_trimat(sum(border_trimat==border_point(j,1),2)+sum(border_trimat==border_point(j,2),2)==2,:);
    %判断中心点是否在三角形内
    [t_x1,t_y1,~]=maketricenter(xdot(temp_trimat(1),:),xdot(temp_trimat(2),:),xdot(temp_trimat(3),:));%求中心
    
    panduan=pointintriangle(xdot(temp_trimat(1),:),xdot(temp_trimat(2),:),xdot(temp_trimat(3),:),[t_x1,t_y1]);
    %求边的中点
    t_x2=(xdot(border_point(j,1),1)+xdot(border_point(j,2),1))/2;
    t_y2=(xdot(border_point(j,1),2)+xdot(border_point(j,2),2))/2;
    if panduan==1
        %做中心-边缘的延长线
        %这里用到了边缘在01这个条件
        t_xy3=[t_x1,t_y1]+[t_x2-t_x1,t_y2-t_y1]*sqrt(2)/sqrt((t_x2-t_x1)^2+(t_y2-t_y1)^2);
        plot([t_x1,t_xy3(1)],[t_y1,t_xy3(2)],'color',[0,0.4,0])
    elseif ~(t_x1<0||t_x1>1||t_y1<0||t_y1>1)
        %判断点是否在边与边框的三角内，如果在，做中心的延长线
        %如果不在，做中心-边缘的延长线
        %或者改成判断点是否在多边形内
        
        t_t=pointinmutiangle(xdot,[border_point(1,1);border_point(:,2)],[t_x1,t_y1]);
        if t_t==1
            t_xy3=[t_x1,t_y1]+[t_x2-t_x1,t_y2-t_y1]*sqrt(2)/sqrt((t_x2-t_x1)^2+(t_y2-t_y1)^2);
            plot([t_x1,t_xy3(1)],[t_y1,t_xy3(2)],'color',[0,0.4,0])
        else
            t_xy3=[t_x1,t_y1]+[t_x1-t_x2,t_y1-t_y2]*1/sqrt((t_x2-t_x1)^2+(t_y2-t_y1)^2);
            plot([t_x1,t_xy3(1)],[t_y1,t_xy3(2)],'color',[0,0.4,0])
        end
    end
end

scatter(xdot(:,1),xdot(:,2),5,[0,0.4,0],'filled')
hold off

%第3部分  多边形面的识别****************************************************************************
%1先规划出多边形预设矩阵（找出xdot数组中出现次数最多的数），行个数等于三角形外接圆中心点的个数
%2选取中心点，然后依次找出一圈三角形（共点），之后依次连接这一圈三角形的外接圆就是泰森多边形
%3对于边缘点，要结合边缘考虑，画出边缘线和延长射线的交点，就是了。还是依次画出，如果点在边缘外，就忽略，在边缘内，就记录。
%4选取上一步记录的三角形最外侧三角，做中垂线

%初始化面

% load('color_Sky02_h.mat')

figure(4)
% colormap(mycolor)
xlim([0,1]);ylim([0,1]);
%依次根据xdot来循环
for j=4:size(xdot,1)
    %trimatcenter
    [temp_trimat,temp_trimat_no,panduan]=findpoint2tri(j,trimat);%找出这一圈三角形
    if panduan
        %直接把temp_trimat_no的点当做泰森多边形即可
        
        patch('Faces',temp_trimat_no,'Vertices',trimatcenter,'FaceVertexCData',rand(1,1),'FaceColor','flat');
        'hyh';
    else
        %需要做边缘化处理
        %如果最终三角形不是边缘三角形，要注意不能适用内外部延长的准则，要用连接法则
        %选出中心点在边界内的一圈三角形
        [temp_trimat,temp_trimat_no,delleft,delright]=selecttemp_trimat(temp_trimat,temp_trimat_no,trimatcenter);
        t_t=1;
            % 如果selecttemp_trimat删除了边上的点，那么做边缘延长线的话就用和删除点之间作为连线，和边相交即可
            %即如果delleft,delright=0，照旧。如果不是0，利用temp_trimat_no(1)和delleft做连线（创建一个公式）
        tempboderedge=trimatcenter(temp_trimat_no,:);
        %边缘延长线1
        if delleft==0
            tempedge=temp_trimat(1,[1,2]);
            tempboderdot1=edgepointfind(tempedge,xdot,trimatcenter(temp_trimat_no(1),:),border_point);%获取边缘点
            if size(tempboderdot1,1)==0
                t_t=0;%边缘点超出，不再画面
            end
        else
            tempboderdot1=edgepointfind2(trimatcenter(temp_trimat_no(1),:),trimatcenter(delleft,:));
        end
        tempboderedge=[tempboderdot1;tempboderedge];
        
        %边缘延长线2
        if delright==0
            tempedge=temp_trimat(end,[1,3]);
            tempboderdot2=edgepointfind(tempedge,xdot,trimatcenter(temp_trimat_no(end),:),border_point);%获取边缘点
            if size(tempboderdot2,1)==0
                t_t=0;%边缘点超出，不再画面
            end
        else
            tempboderdot2=edgepointfind2(trimatcenter(temp_trimat_no(end),:),trimatcenter(delright,:));
        end
        tempboderedge=[tempboderedge;tempboderdot2];

        %绘制边缘图形
        
        if t_t==1
            if tempboderdot1(1)~=tempboderdot2(1)
                if tempboderdot1(2)~=tempboderdot2(2)
                    %边缘延长线3(边界角点
                    tempboderedge=[tempboderedge;maketempboderdot(tempboderdot1,tempboderdot2)];
                end
            end
            patch('Faces',1:length(tempboderedge),'Vertices',tempboderedge,'FaceVertexCData',rand(1,1),'FaceColor','flat');
            'hyh2';
        end
        
    end
    
end








%判断点在三角形外接圆的哪个部分
function panduan=whereispoint(xy1,xy2,xy3,xy0)
%判断点在三角形外接圆的哪个部分
[a,b,r2]=maketricenter(xy1,xy2,xy3);
x0=xy0(1);y0=xy0(2);
if a+sqrt(r2) 0 ||...
        (((l2x1-l1x1)*(l1y2-l1y1)-(l2y1-l1y1)*(l1x2-l1x1))*...
        ((l2x2-l1x1)*(l1y2-l1y1)-(l2y2-l1y1)*(l1x2-l1x1))) > 0)
        %如果判断为真，则不会相交
        panduan=0;
    else
        panduan=1;
    end
end
end

%两个向量做差积
function t=crossdot(xy1,xy2)
x1=xy1(1);y1=xy1(2);
x2=xy2(1);y2=xy2(2);
t=x1*y2-y1*x2;
end

%点是否在三角形内
function panduan=pointintriangle(xy1,xy2,xy3,xy0)
x1=xy1(1);y1=xy1(2);
x2=xy2(1);y2=xy2(2);
x3=xy3(1);y3=xy3(2);
x0=xy0(1);y0=xy0(2);
PA=[x1-x0,y1-y0];PB=[x2-x0,y2-y0];PC=[x3-x0,y3-y0];
%利用差积同正或同负号来判断是否在三角内
t1=crossdot(PA,PB);
t2=crossdot(PB,PC);
t3=crossdot(PC,PA);
if abs(sign(t1)+sign(t2)+sign(t3))==3
    panduan=1;
else
    panduan=0;
end

end

%点是否在多边形内
function panduan=pointinmutiangle(xdot,d_no,xy0)
%d_no符合12341的格式，收尾相连
Ndot=xdot(d_no,:);
PN=[Ndot(:,1)-xy0(1),Ndot(:,2)-xy0(2)];
tn=zeros(length(d_no)-1,1);
for j=1:length(d_no)-1
    tn(j)=crossdot(PN(j,:),PN(j+1,:));
end
%利用差积同正或同负号来判断是否在三角内

if abs(sum(sign(tn)))==length(d_no)-1
    panduan=1;
else
    panduan=0;
end

end

%做出同时具有一个中心点的一圈三角形，按照相接顺序排序
function [temp_trimat,temp_trimat_no,panduan]=findpoint2tri(j,trimat)
temp_trimat_no=1:size(trimat,1);
panduan=1;
temp_trimat=trimat(logical(sum(trimat==j,2)),:);
temp_trimat_no=temp_trimat_no(logical(sum(trimat==j,2)));
%把j放到每行第一个
for k=1:size(temp_trimat,1)
    temp_trimat(k,[find(temp_trimat(k,:)==j),1])=temp_trimat(k,[1,find(temp_trimat(k,:)==j)]);
end
%如果有一个点只出现过一次，把这个点包含的三角形放到第一行
tN2=tabulate(reshape(temp_trimat,[],1));
tN3=tN2((tN2(:,2)==1),1);
%其实如果中心点不在范围内也最好单列出来，挖坑

if size(tN3,1)~=0
    tN3=tN3(1);
    tN=find(sum(temp_trimat==tN3,2));
    temp_trimat([1,tN],:)=temp_trimat([tN,1],:);
    temp_trimat_no([1,tN])=temp_trimat_no([tN,1]);
    panduan=0;
    if temp_trimat(1,3)==tN3
        temp_trimat(1,[2,3])=temp_trimat(1,[3,2]);
    end
end


%把边首尾排序一遍
for k=2:size(temp_trimat,1)
    
    tN=find(sum(temp_trimat==temp_trimat(k-1,3),2));
    tN(tN==k-1)=[];
    temp_trimat([tN,k],:)=temp_trimat([k,tN],:);
    if temp_trimat(k-1,3)~=temp_trimat(k,2)
        temp_trimat(k,[2,3])=temp_trimat(k,[3,2]);
    end
    temp_trimat_no([tN,k])=temp_trimat_no([k,tN]);
end
end

%做出一点对边缘的中垂线，得到边缘点坐标
function tempboderdot=edgepointfind(tempedge,xdot,xy0,border_point)

x0=xy0(1);y0=xy0(2);
%判断中心点是否在大图形内
d_no=[border_point(1,1);border_point(:,2)];
panduan=pointinmutiangle(xdot,d_no,xy0);
%求边的中点
xz=(xdot(tempedge(1),1)+xdot(tempedge(2),1))/2;
yz=(xdot(tempedge(1),2)+xdot(tempedge(2),2))/2;
%做中心点延长线，得到一条超长线段定为2得了,用到了边界为1这个条件
panduan2=true;
if panduan
    %在内部，做中心到边缘延长线即可
    t_xy1=[x0,y0]+[xz-x0,yz-y0]*2/sqrt((xz-x0)^2+(yz-y0)^2);
    
else
    if ~(x0<0||x0>1||y0<0||y0>1)
    %在外部,但是没超出边界，做中心到反向边缘
        t_xy1=[x0,y0]-[xz-x0,yz-y0]*2/sqrt((xz-x0)^2+(yz-y0)^2);
    else
        %在边界外
        panduan2=false;
        tempboderdot=[];%返回空矩阵
    end
end

if panduan2
    %判断是4个边哪一个
    [xy3,xy4]=select4edge(xy0,t_xy1);
    %做4点求交点运算
    tempboderdot=crosspoint(xy0,t_xy1,xy3,xy4);
end
%     panduan
%     d_no
%     xy0
%     t_xy1
%     tempboderdot
end

%做出边缘界外连线，得到边缘点坐标
function tempboderdot1=edgepointfind2(xy1,xy2)
[xy3,xy4]=select4edge(xy1,xy2);
tempboderdot1=crosspoint(xy1,xy2,xy3,xy4);
end
%判断射线会与哪条边相交
function [xy3,xy4]=select4edge(xy0,xy1)
deg01=angle((0-xy0(1))+(0-xy0(2))*1i);%左下00
deg02=angle((1-xy0(1))+(0-xy0(2))*1i);%10
deg03=angle((1-xy0(1))+(1-xy0(2))*1i);%11
deg04=angle((0-xy0(1))+(1-xy0(2))*1i);%01
deg00=angle((xy1(1)-xy0(1))+(xy1(2)-xy0(2))*1i);
[~,I]=sort([deg00,deg01,deg02,deg03,deg04]);
k=find(I==1);
switch k
    case 1
        xy3=[0,0];xy4=[0,1];
    case 2
        xy3=[0,0];xy4=[1,0];
    case 3
        xy3=[1,0];xy4=[1,1];
    case 4
        xy3=[0,1];xy4=[1,1];
    case 5
        xy3=[0,0];xy4=[0,1];
end
end

%求两条线交点
function xy0=crosspoint(xy1,xy2,xy5,xy6)
a1=(xy2(2)-xy1(2));b1=(xy1(1)-xy2(1));c1=xy1(1)*xy2(2)-xy2(1)*xy1(2);
a2=(xy6(2)-xy5(2));b2=(xy5(1)-xy6(1));c2=xy5(1)*xy6(2)-xy6(1)*xy5(2);
xy0=[det([c1,b1;c2,b2])/det([a1,b1;a2,b2]),det([a1,c1;a2,c2])/det([a1,b1;a2,b2])];
end


%删除所有中心点超出边界的三角形
function [temp_trimat,temp_trimat_no,delleft,delright]=selecttemp_trimat(temp_trimat,temp_trimat_no,trimatcenter)
delleft=0;delright=0;
for j=1:size(temp_trimat,1)
    centerdot=trimatcenter(temp_trimat_no(j),:);
    if and(and(0

输出的网格

未上色的Voronoi图

彩色Voronoi图

结束