第二章 坐标系及其转换(车道线感知)

@[TOC](第二章 坐标系极其转换(车道线感知))

前言

近期参与到了手写AI的车道线检测的学习中去，以此系列笔记记录学习与思考的全过程。车道线检测系列会持续更新，力求完整精炼，引人启示。所需前期知识，可以结合手写AI进行系统的学习。

一 先导与重点

文章主要介绍自动驾驶技术中几种常用的坐标系统，以及他们之间如何完成关联和转换，最终构建出统一的环境模型。这里重点理解自车到相机刚体转换(外参)，相机到图像转换(内参)，图像到像素有单位转换。3d向2d转换会有相应的畸变，平移等。

重点：自车坐标系<->相机机体坐标系<->像平面坐标系<->像素坐标系
难点：要考虑图像畸变，去畸变和加畸变都是在像平面上去补偿

二 简介

视觉系统一共有四个坐标系：像素平面坐标系（u,v）、图像坐标系（x,y）、相机坐标系（$x_c,y_c,z_c$）和世界坐标系（$x_{\omega },y_{\omega },z_{\omega }$）。每种坐标系之间均存在联系，那么如何通过图像像素坐标定位到世界坐标系的坐标，需要通过相机标定来解决，其中关键的算法部分在于坐标系转换，而变换则需要通过齐次坐标的表示方式来完成。

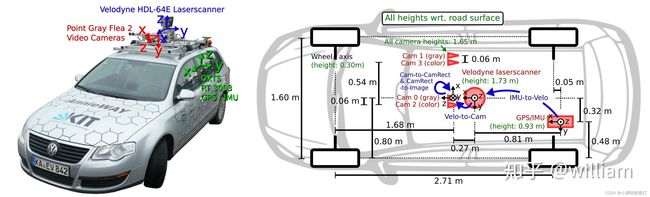
三 各个传感器坐标系

3.1 相机坐标系统

摄像头的作用是把三维世界中的形状、颜色信息，压缩到一张二维图像上。基于摄像头的感知算法则是从二维图像中提取并还原三维世界中的元素和信息，如车道线，车辆、行人等，并计算他们与自己的相对位置。
感知算法和相机相关的坐标系有图像坐标系（像素坐标系）、摄像机坐标系、像平面坐标系

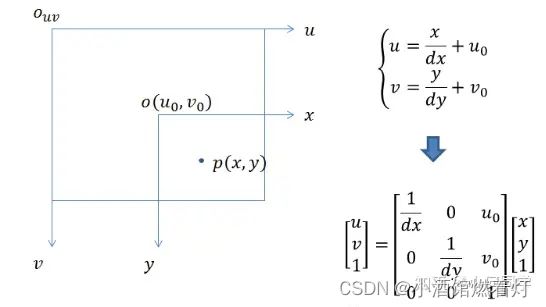
3.1.1 图像坐标系（or 像素坐标系）

电脑上存储的照片或图像，一般以左上角为原点，向右为x正方向，向下为y正方向，单位以“像素”最为常用。图像坐标系为二维坐标系，标记为(Xv, Yv)。

3.1.2 摄像机坐标系

由于图像坐标系向右为x，向下为y，所以摄像机坐标系以镜头主光轴中心为原点，一般向右为x正方向，向下为y正方向，向前为z正方向。这样，x，y方向与图像坐标系的方向吻合，z方向即为景深，摄像机坐标系记为(Xc, Yc)

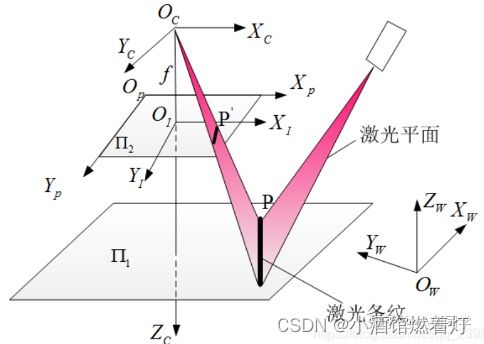
3.1.3 像平面坐标系（or 成像坐标系）

为了能够**定量描述三维空间到二维图像的映射关系，**图形学里引入了像平面坐标系。它是摄像机坐标系的一个平移，中心仍在摄像机主光轴上，距离光轴中心的距离等于摄像机的焦距
我们知道摄像机会在光轴中心后方的底片上成一个缩小的倒像，是真正的像平面(Xf, Yf)。但是为了分析和计算方便，我们会在光轴中心前方设立一个虚拟像平面。虚拟像平面上的成像为正像，大小与真实倒像相同

3.5 世界坐标系

根据情况而定，可以表示任何物体，此时是由于相机而引入的。单位m。

世界坐标系$O_w{X}_w{Y}_w{Z}_w$ ，相机坐标系$O_c{X}_c{Y}_c{Z}_c$ ，成像坐标系$O_I{X}_I{Y}_I{Z}_I$ 及像素坐标系$O_p{X}_p{Y}_p{Z}_p$

四 Lidar 坐标系

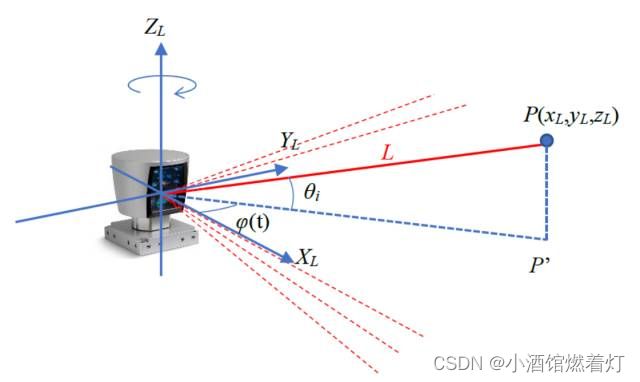
Lidar (Light Detection and Ranging) 是一种远程感测技术，使用激光光束测量与物体的距离。360度旋转发射射线，根据不同目标反射率不同反射而形成电云。在自动驾驶和机器人领域，Lidar常被用作一个主要的传感器来获取周围环境的3D信息。在多数情况下，Lidar坐标系为右手坐标系，但具体定义可能会因Lidar制造商而异。

4.1 定义

X轴: 通常指向Lidar前方。当激光束直接向前发射时，与该方向的距离测量会在X轴上产生一个正值。
Y轴: 通常指向Lidar的左侧。当激光束直接向左侧发射时，与该方向的距离测量会在Y轴上产生一个正值。
Z轴: 通常指向Lidar的上方，与X和Y轴垂直。高度测量通常沿Z轴进行，正值代表物体高于Lidar设备，而负值代表低于Lidar设备。

4.2 重要性

• 车载Lidar系统的坐标系与车辆坐标系可能不完全对齐，需要一个转换矩阵来在两者之间进行坐标变换。
• 数据标注、地图生成、物体检测等任务需要明确Lidar坐标系的定义。
• 对于与其他传感器的数据融合，例如摄像头，知道各自的坐标系是非常关键的，以便进行正确的数据对齐和融合。
• 当与摄像头、雷达或其他传感器进行数据融合时，通常需要知道Lidar与这些传感器之间的外部标定参数（例如，旋转和平移矩阵），以便在它们之间进行坐标变换。

五 自车坐标系

一般环境中选择一个参考坐标系来描述传感器和物体的位置，该坐标系称为世界坐标系；自车坐标系一般指的是以车体后轴中心为原点（因为后轴中心不会随着车摆动而发生相对变化），左前上或右前上的空间坐标系，左（右）一般为横向，前一般为纵向，上指地面以上空间，坐标系随着车运动而运动。所有的下游需要感知输出的目标都要在自车坐标系下面，BEV视角目标也是指的在这个坐标系下

一般三维空间坐标系用三个正交轴X,Y,Z表示物体的位置，用绕这三个正交轴的旋转角度（roll 滚动角, pitch 俯仰角, yaw 偏航角）表示物体的姿态。时间坐标系只有一个维度。为了表述方便，我们一般将空间坐标和时间坐标分开讨论。

六 摄像机的内参和外参

6.1 相机内参

内参用来确定摄像机从三维空间到二维图像的投影关系。
主要包含三个参数，相机主点，相机焦距，畸变系数。内参一般由商家给定，也可以进行摄像机标定。在自动驾驶应用中**，摄像机的内参为常数，使用中不会发生变化**，但需要在使用前做好标定工作。摄像机的拍摄过程，可以抽象成是从三维摄像机坐标系映射到二维像平面坐标系，再映射到图像坐标系的过程。

6.1 焦距 (f)

• 它描述了图像传感器与摄像机的透镜之间的距离。通常用两个参数 ($f_x$) 和 ($f_y$) 来表示，分别对应于图像的x轴和y轴。
• 在很多情况下，我们假定 ($f_x=f_y$)，这意味着像素在两个方向上都是正方形的。

6.2 主点

• 它是图像中的一个点，通常接近图像的中心。它是3D空间中的点投影到图像平面时所对应的2D点。
• 通常用两个参数 ($c_x$) 和 ($c_y$) 表示，它们对应于图像的x轴和y轴上的坐标。

6.3 畸变系数

• 真实摄像机的透镜可能会引入畸变，导致图像失真。常见的畸变有径向畸变和切向畸变。
• 常用的径向畸变系数为 ($k_1,k_2,k_3$)。
• 切向畸变系数为 ($p_1,p_2$)。

摄像机的内参通常可以表示为一个矩阵：

K = [ f x 0 c x 0 f y c y 0 0 1 ] K = \begin{bmatrix} f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \\ \end{bmatrix} K= ​fx​00​0fy​0​cx​cy​1​ ​

这个矩阵通常被称为内参矩阵或相机矩阵。

6.2 相机外参

通过二维图像推断物体在三维摄像机坐标系中的位置，例如获得距离深度信息。从二维图像中获取三维距离信息，如果需要获得物体在世界坐标系中的位置，则还需要知道摄像机在世界坐标系中的位姿。
这一位姿表示被称为摄像机的外部参数，简称外参，用来决定摄像机坐标与世界坐标系之间相对位置关系。自动驾驶应用中，得到这一位置关系还需要一系列的标定和定位工作。
相机相对其它坐标系，旋转+平移矩阵，其中旋转外参与上述欧拉角【yaw，patch，roll】，旋转顺序一般为（z-y-x), 单位度；平移外参，相机到目标坐标系中的平移距离，单位米

七 自车坐标系与世界坐标系

7.1 自车坐标系 (Vehicle Coordinate System)

• 这是固定在车辆上的坐标系。
• 通常，X轴指向车辆的前方、Y轴指向车辆的右侧（或左侧，这取决于约定）、Z轴指向车辆的上方。
• 这个坐标系的原点通常位于车辆的某个固定点，例如车辆的中心、车辆的后轴等，这取决于特定的应用和约定。

7.2 世界坐标系 (World Coordinate System)

• 这是一个固定的、全局的坐标系，用于描述环境中的物体和车辆。
• 世界坐标系的原点和方向通常根据特定的应用或场景来选择。例如，它可以定位在一个地图的某个固定点，或者是某个场景的中心。
• 世界坐标系为多个实体提供了一个共同的参考框架，允许它们之间进行相对定位和导航。

关系与转换：

• 由于车辆在世界中是移动的，所以自车坐标系和世界坐标系之间的关系是时间变化的。
• 为了在这两个坐标系之间进行转换，通常需要一个转换矩阵或变换（通常由旋转和平移组成）。这个转换可以通过各种传感器（例如GPS、IMU、激光雷达）和算法（例如SLAM）获得。
• 转换可以表示为一个4x4的齐次坐标矩阵，允许我们从一个坐标系转换到另一个坐标系。

大多数情况下自车坐标系等同于世界坐标系，本文章也是这么理解的。

八 坐标系之间转换关系

8.1 从世界坐标系到相机坐标系

物体之间的坐标系变换都可以表示坐标系的旋转变换加上平移变换，则世界坐标系到相机坐标系的转换关系也是如此。绕着不同的轴旋转不同的角度得到不同的旋转矩阵。
绕Z轴旋转θ示意图:

• 旋转：
  坐标变换：根据相似三角形和勾股定理可以推出：
  $$\{\begin{array}{c}x=x^{\prime }cos\theta -y^{\prime }sin\theta \\ y=x^{\prime }sin\theta +y^{\prime }cos\theta \\ z=z^{\prime }\end{array}$$
  转换成矩阵形式如下:
  [ x y z ] = [ c o s θ − s i n θ 0 s i n θ c o s θ 0 0 0 1 ] [ x ′ y ′ z ′ ] \begin{bmatrix}x\\y\\z\end{bmatrix}=\begin{bmatrix}cos\theta&-sin\theta&0\\sin\theta&cos\theta&0\\0&0&1\end{bmatrix}\begin{bmatrix}x'\\y'\\z'\end{bmatrix} ​xyz​ ​= ​cosθsinθ0​−sinθcosθ0​001​ ​ ​x′y′z′​ ​
  R 1 [ x ′ y ′ z ′ ] \left.R_1\left[\begin{matrix}x'\\y'\\z'\end{matrix}\right.\right] R1​ ​x′y′z′​ ​
  其他绕x,y,转也类似，可以得到:
  [ x y z ] = [ 1 0 0 0 c o s ϕ s i n ϕ 0 − s i n ϕ c o s ϕ ] [ x ′ y ′ z ′ ] [ x y z ] = [ c o s ω 0 − s i n ω 0 1 0 s i n ω 0 c o s ω ] [ x ′ y ′ z ′ ] \begin{aligned}&\begin{bmatrix}x\\y\\z\end{bmatrix}=\begin{bmatrix}1&0&0\\0&cos\phi&sin\phi\\0&-sin\phi&cos\phi\end{bmatrix}\begin{bmatrix}x'\\y'\\z'\end{bmatrix}\\&\begin{bmatrix}x\\y\\z\end{bmatrix}=\begin{bmatrix}cos\omega&0&-sin\omega\\0&1&0\\sin\omega&0&cos\omega\end{bmatrix}\begin{bmatrix}x'\\y'\\z'\end{bmatrix}\end{aligned} ​ ​xyz​ ​= ​100​0cosϕ−sinϕ​0sinϕcosϕ​ ​ ​x′y′z′​ ​ ​xyz​ ​= ​cosω0sinω​010​−sinω0cosω​ ​ ​x′y′z′​ ​​

最后可以简单总结为旋转矩阵：$R=R_1{R}_2{R}_3$

• 平移:
  平移相机坐标点（$x_c,y_c,z_c$）平移距离为（$t_x,t_y,t_z$）到世界坐标点（$x_{\omega },y_{\omega },z_{\omega }$）：
  [ x ω y ω z ω 1 ] = [ 1 0 0 t x 0 1 0 t y 0 0 1 t z 0 0 0 1 ] [ x c y c z c 1 ] \begin{bmatrix}x_\omega\\y_\omega\\z_\omega\\1\end{bmatrix}=\begin{bmatrix}1&0&0&tx\\0&1&0&t_y\\0&0&1&t_z\\0&0&0&1\end{bmatrix}\begin{bmatrix}x_c\\y_c\\z_c\\1\end{bmatrix} ​xω​yω​zω​1​ ​= ​1000​0100​0010​txty​tz​1​ ​ ​xc​yc​zc​1​ ​

如果坐标点（$x_c,y_c,z_c$）绕X，Y，Z轴分别旋转α，β，γ度，则最终的表达式为：
$$[X_W{Y}_W{Z}_{W}1]=[X_c{Y}_c{Z}_{c}1]\left[\begin{array}{cc}R& 0\\ T& 1\end{array}\right]$$
其中：
$$\begin{array}{rl}\mathrm{R}& =R_x{R}_y{R}_z\\ T& =\left[\begin{array}{ccc}{t}_x& t_y& t_z\end{array}\right]\end{array}$$

8.2 相机坐标系到图像坐标系

从相机坐标系到图像坐标系，属于透视投影关系，从3D转换到2D。 也可以看成是针孔模型的改变模型。满足三角形相似定理。

8.3 图像坐标系到像素坐标系

此时与前面的坐标系变换不同，此时没有旋转变换，但是坐标原点位置不一致，大小不一致，则设计伸缩变换及平移变换。

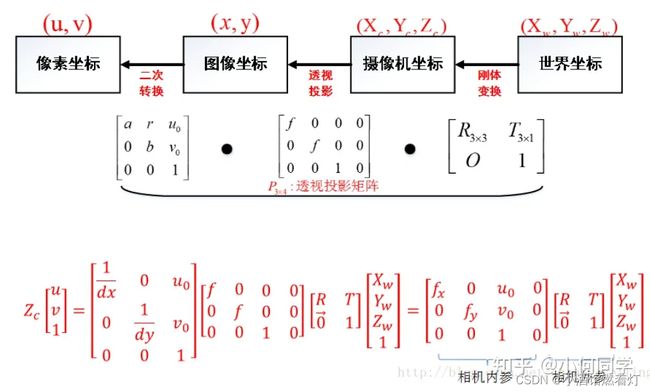
8.4 四个坐标系之间的关系

[ X w Y w Z w 1 ] = [ R T 0 1 ] [ Z c f 0 0 0 Z c f 0 0 0 Z c 0 0 1 ] [ d x 0 − u 0 d x 0 d y − ν 0 d y 0 0 1 ] [ u v 1 ] \begin{bmatrix}X_w\\Y_w\\Z_w\\1\end{bmatrix}=\begin{bmatrix}R&T\\0&1\end{bmatrix}\begin{bmatrix}\dfrac{Z_c}{f}&0&0\\0&\dfrac{Z_c}{f}&0\\0&0&Z_c\\0&0&1\end{bmatrix}\begin{bmatrix}dx&0&-u_0dx\\0&dy&-\nu_0dy\\0&0&1\end{bmatrix}\begin{bmatrix}u\\v\\1\end{bmatrix} ​Xw​Yw​Zw​1​ ​=[R0​T1​] ​fZc​​000​0fZc​​00​00Zc​1​ ​ ​dx00​0dy0​−u0​dx−ν0​dy1​ ​ ​uv1​ ​

通过最终的转换关系来看，一个三维中的坐标点，的确可以在图像中找到一个对应的像素点，但是反过来，通过图像中的一个点找到它在三维中对应的点就很成了一个问题，因为我们并不知道等式左边的$z_c$的值

红框内即为外参，R和T分别为旋转和平移量。内参为是相机固有的属性，实际上就是焦距f，像元尺寸dx,dy。很明显$z_c$，表示的是点离光轴的距离

九 总结

梳理了自动驾驶的各种坐标系，展现自动驾驶各坐标系间的关系，最终得到像素坐标系与世界坐标系的转换关系。