【深度学习】pytorch——线性回归

笔记为自我总结整理的学习笔记，若有错误欢迎指出哟~

深度学习专栏链接：
http://t.csdnimg.cn/dscW7

线性回归简介

线性回归是一种用于建立特征和目标变量之间线性关系的统计学习方法。它假设特征和目标变量之间存在一个线性的关系，并试图通过拟合最佳的线性函数来预测目标变量。

线性回归模型的一般形式可以表示为：

$$y=w_0+w_1{x}_1+w_2{x}_2+\dots +w_n{x}_n$$

其中，$y$ 是目标变量（或因变量），$x_1,x_2,\dots ,x_n$ 是特征变量（或自变量），$w_0,w_1,w_2,\dots ,w_n$ 是模型的参数，分别对应截距和各个特征的权重。

线性回归模型的训练过程就是寻找最优的参数 $w_0,w_1,w_2,\dots ,w_n$ 来使得模型的预测值与实际值之间的差异最小化。

公式说明

以下是代码涉及到的数学公式

1. 线性回归模型

线性回归模型用于建立特征 $x$ 和目标变量 $y$ 之间的线性关系。在本代码中，线性回归模型被表示为：

$$y=wx+b$$

其中，$w$ 是权重（即斜率），$b$ 是偏置（即截距），$x$ 是输入特征，$y$ 是预测值。

2. 损失函数

损失函数用于衡量模型预测值与实际标签之间的差异。在本代码中，使用的损失函数是均方误差（Mean Squared Error，MSE）：

$$loss=\frac{1}{2n}\sum _{i=1}^n(y_{pred}^{(i)}-y^{(i)}{)}^2$$

其中，$y_{pred}^{(i)}$ 是模型的第 $i$ 个样本的预测值，$y^{(i)}$ 是实际标签，$n$ 是样本数量。

3. 其他运算

代码中还涉及到了矩阵乘法、矩阵转置、元素级别的操作等。例如，$x.mm(w)$ 表示将输入特征 $x$ 与权重 $w$ 进行矩阵乘法；$x^T.mm(dy\_pred)$ 表示将输入特征 $x$ 的转置与梯度 $dy\_pred$ 进行矩阵乘法。

完整代码

import torch as t
%matplotlib inline
from matplotlib import pyplot as plt
from IPython import display

device = t.device('cpu') #如果你想用gpu，改成t.device('cuda:0')

# 设置随机数种子，保证在不同电脑上运行时下面的输出一致
t.manual_seed(1000) 

def get_fake_data(batch_size=8):
    ''' 产生随机数据：y=x*2+3，加上了一些噪声'''
    x = t.rand(batch_size, 1, device=device) * 5
    y = x * 2 + 3 +  t.randn(batch_size, 1, device=device)
    return x, y

'''
# 产生的x-y分布
x, y = get_fake_data(batch_size=100)
plt.scatter(x.squeeze().cpu().numpy(), y.squeeze().cpu().numpy())
'''


# 随机初始化参数
w = t.rand(1, 1).to(device)
b = t.zeros(1, 1).to(device)

lr =0.02 # 学习率

for ii in range(500):
    x, y = get_fake_data(batch_size=4)
    
    # forward：计算loss
    y_pred = x.mm(w) + b.expand_as(y) 
    loss = 0.5 * (y_pred - y) ** 2 # 均方误差
    loss = loss.mean()
    
    # backward：手动计算梯度
    dloss = 1
    dy_pred = dloss * (y_pred - y)
    
    dw = x.t().mm(dy_pred)
    db = dy_pred.sum()
    
    # 更新参数
    w.sub_(lr * dw)
    b.sub_(lr * db)
    
    if ii%50 ==0:
        # 画图
        display.clear_output(wait=True)
        x = t.arange(0, 6).view(-1, 1)
        y = x.float().mm(w) + b.expand_as(x)
        plt.plot(x.cpu().numpy(), y.cpu().numpy(),color='b') # predicted
        
        x2, y2 = get_fake_data(batch_size=100) 
        plt.scatter(x2.numpy(), y2.numpy(),color='r') # true data
        
        plt.xlim(0, 5)
        plt.ylim(0, 15)
        plt.show()
        plt.pause(0.5)
        
print('w: ', w.item(), 'b: ', b.item())

输出结果为：

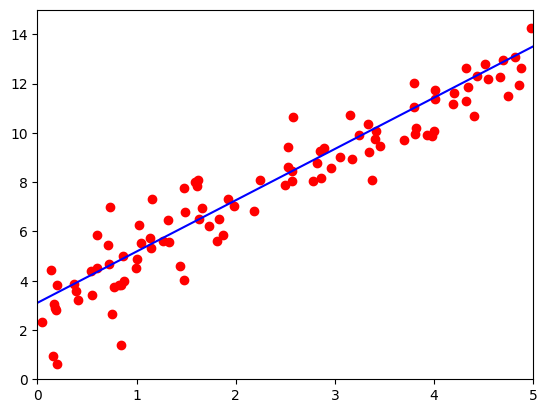
w: 1.9709817171096802 b: 3.1699466705322266

代码解释

1. 导入需要的库：

import torch as t
%matplotlib inline
from matplotlib import pyplot as plt
from IPython import display

导入PyTorch库以及绘图相关的库，%matplotlib inline是Jupyter Notebook中的魔法命令，用于在Notebook中显示绘图。

2. 设置随机数种子：

t.manual_seed(1000)

这行代码设置随机数种子，保证每次运行结果的随机数生成过程一致。

3. 定义生成随机数据的函数：

def get_fake_data(batch_size=8):
    ''' 产生随机数据：y=x*2+3，加上了一些噪声'''
    x = t.rand(batch_size, 1, device=device) * 5
    y = x * 2 + 3 +  t.randn(batch_size, 1, device=device)
    return x, y

该函数用于产生随机的输入特征x和对应的标签y，其中y满足线性关系y = x * 2 + 3，并添加了一些随机噪声。

4. 初始化模型参数：

w = t.rand(1, 1).to(device)
b = t.zeros(1, 1).to(device)

这里使用随机数初始化模型参数w和b，并指定在CPU上进行计算。

5. 设置学习率：

lr = 0.02

学习率lr控制每次参数更新的步长。

6. 进行模型训练：

for ii in range(500):
    # 生成随机数据
    x, y = get_fake_data(batch_size=4)
    
    # forward：计算损失
    y_pred = x.mm(w) + b.expand_as(y)
    loss = 0.5 * (y_pred - y) ** 2
    loss = loss.mean()
    
    # backward：手动计算梯度
    dloss = 1
    dy_pred = dloss * (y_pred - y)
    
    dw = x.t().mm(dy_pred)
    db = dy_pred.sum()
    
    # 更新参数
    w.sub_(lr * dw)
    b.sub_(lr * db)

这里使用一个循环进行模型的训练，每次迭代都包含以下步骤：

• 生成随机数据；
• 前向传播：计算预测值y_pred和损失函数loss；
• 反向传播：手动计算梯度dw和db；
• 更新参数：根据梯度和学习率更新参数w和b。

7. 可视化模型训练过程：

if ii % 50 == 0:
    display.clear_output(wait=True)
    x = t.arange(0, 6).view(-1, 1)
    y = x.float().mm(w) + b.expand_as(x)
    plt.plot(x.cpu().numpy(), y.cpu().numpy(), color='b') # predicted line
    
    x2, y2 = get_fake_data(batch_size=100)
    plt.scatter(x2.numpy(), y2.numpy(), color='r') # true data
    
    plt.xlim(0, 5)
    plt.ylim(0, 15)
    plt.show()
    plt.pause(0.5)

这部分代码用于可视化模型训练的过程，每50次迭代将当前参数下的预测结果以蓝色线条的形式绘制出来，并将随机生成的100个样本以红色散点图显示出来。

8. 输出最终训练得到的参数：

print('w: ', w.item(), 'b: ', b.item())

输出训练得到的参数w和b的值。