力扣刷题笔记之二
目录
滑动窗口——至少有 K 个重复字符的最长子串(力扣395)
层序遍历的变形——求二叉树右视所能看到的节点的值
二分法的一些感悟
二叉树遍历的非递归方式
缺失的第一个正数(力扣41题)
买卖股票的最佳时机(力扣123题)
背包问题
反转链表的递归
合并链表的递归
回溯法
全排列(力扣46)
全排列-Ⅱ(力扣47题)
全排列Ⅲ-字符串全排列(剑指37)
子集(力扣78题)
子集Ⅱ(力扣90题)
组合总和(力扣39题)
组合总和Ⅱ(力扣40)
验证二叉搜索树(力扣98)
最小路径和(力扣第64题)
动态规划之最小串(力扣718,1143题)
与最小串动态规划思路相似的题——最大正方形(力扣221)
岛屿问题
单调栈问题
背包问题
最长公共子串和最长公共子序列
滑动窗口——至少有 K 个重复字符的最长子串(力扣395)
滑动窗口多用于数组和字符串中,寻找某个符合条件的子字符串或子数组,并且保证它们都是连续的
给你一个字符串 s 和一个整数 k ,请你找出 s 中的最长子串, 要求该子串中的每一字符出现次数都不少于 k 。返回这一子串的长度。
s仅由小写英文字母组成示例 1: 输入:s = "aaabb", k = 3 输出:3
解释:最长子串为 "aaa" ,其中 'a' 重复了 3 次。
此题算是滑动窗口里比较难的题了,难点在于它的滑动窗口的边界不好判断。
滑动窗口算法具有一个性质叫做“单调性”,就是在扩张滑动窗口的过程中,当左边界的端点确定时,右边界的端点可以向右移动,而之后不用回退;相似的,在收缩滑动窗口的过程中,右边界端点值固定,左边界端点可以向左移动,后期不用回退。
当前窗口的状态值确定, 并且更具当前状态,右边界端点右移或左边界端点左移所产生的一下个滑动窗口只会有一种确定的状态,这是才可以采用滑动窗口的方法。
举个例子 对于字符串cbdbbaaa,如果要求其中长度最长的不含重复字符的最大子字符串的长度。
假如当前遍历到cbd窗口,那么它的下一个窗口cbdb的不含重复字符的最大子字符串的长度还是确定的,并不会因为新增的字符b而有二义性。
而对于字符串bbaaadbcd 像题目中要求其最长子字符串的长度,子字符串中所有字符出现次数大于等于k 此时如果遍历到bbaaa窗口,如果下一个字符是'b''最长子字符串的长度是6,如果下一个字符不是'b',那么最长子字符串的长度为3,(此时右边界端点需要回退)。也就是说滑动窗口的状态与下一个加入的字符的具体值有关。
此题无法直接用滑动窗口来解决,可以将问题换一种设问方式:
给你一个字符串 s 和一个整数 k ,请你找出 s 中的最长子串, 要求该子串中的每一字符出现次数都不少于 k 。并且该子串中不同的元素一共有i个,返回这一子串的长度。
因为小写字母总共只有26个,也就是一串字符串,按它里面所含的不同字符的数量来区分,总共就26种情况,对这26种情况下的最长子串分别求取其最大值,然后取较大者。
public:
int longestSubstring(string s, int k) {
int res = 0, len = s.length();
for(int i = 0; i < 26; i++){
vector memory(26,0);
//total指的是字符串中不重复的字符的数量,matched指的是这total个字符里,数量大于等于k的个数
for(int left = 0, right = 0, total = 0, matched = 0; right < len; right++){
int num = ++memory[s[right] - 'a'];
if(num == 1) total++;//由0变成1 表示有新的元素加入
if(num == k) matched++;//由k-1 变为 k 表示有一个字符的数量符合题意
while(total > i){
int n = --memory[s[left++] - 'a'];
if(n == 0) total--;
if(n == k -1) matched--;
}
if(matched == total) res = max(res, right - left + 1);
}
}
return res;
}
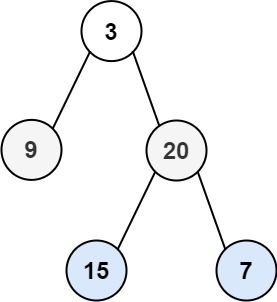
}; 层序遍历的变形——求二叉树右视所能看到的节点的值
输入:root = [3,9,20,null,null,15,7] 输出:[3, 20, 7]
利用层序遍历的知识,建立一个队列数据结构,每次存储当前层的节点个数(也就是当前队列中元素的个数),右视图所得到的节点就是当前队列中尾部的元素。
class Solution {
public:
vector rightView(TreeNode* root) {
vector res;
if(!root) return res;
queue memory;
memory.push(root);
while(!memory.empty()){
int len = memory.size();//记录当前层的节点的个数
for(int i = 0; i < len; i++){
TreeNode * temp = memory.front();
memory.pop();
if (i== len -1) res.push_back(temp->val);//得到最右边的端点
if(temp -> left) memory.push(temp -> left);
if(temp -> right) memory.push(temp -> right);
}
}
return res;
}
}; 二分法的一些感悟
常见二分法的一个基本的要求就是是用二分法的数组要是有序。因为二分法实际上是通过不断地缩小寻找范围来查找的,只有有序数组才能判断出待查找数字位于哪一个范围中。
用二分法来查找一个有序数组nums中的元素,实际上就是一次次的比较nums[mid]与目标值的大小过程,但是这与遍历整个数组不同的是,nums[mid]与目标值比较的次数较少,这也是为什么二分法时间复杂度更低的原因。它比较的范围从n个到n/2个到n/4个..........,因为数组有序,所以可以把数组分为两个部分或三个,每次都能确定出数组中的一段数据,这一段数据中一定不包含目标值,对剩下的部分进行二分查找(这也是二分法代码编写的核心),这样的话时间复杂度就是logn级别的。
二分法查找特定元素停止的情况只有两种,一个是在二分查找的过程中,nums[mid]与目标值相等,这时直接返回,另一种是将数组里所有的可能的元素全部检索了一边,但都没有符合条件的元素。
进一步的,其实二分法不要求数组一定有序也是可以的,只要能够存在一种稳定的特性,每次能够明确的判别:数组中有一部分是一定不包含目标元素的,那么就能用二分法。而有序数组是这种方法里的一种,它能一次同时进行多次(次数是当前数组元素个数一半)的判别(即这些元素里一定没有目标元素),这也就使其时间复杂度大大降低。
题外话:其实换一个角度看,二分法非常“奢侈”,每次对于当前数组,都只取它的中位数(num[mid])进行判断,判断完之后,剩下的元素一概不进行判断,直接进行分组,在下一组数据继续进行这样的操作,而它这么做的底气就是数组是有序数组。
二叉树遍历的非递归方式
前序
void fun(node){
if(!node) return;
cout << node ->val;
fun(code -> left);
fun(code -> right);
}class Solution {
public:
vector res;
vector preorderTraversal(TreeNode* root) {
TreeNode * curr = root;
stack memory;
while(!memory.empty()|| curr){
while(curr){
memory.push(curr);
res.push_back(curr -> val);
curr = curr -> left;
}
curr = memory.top();
memory.pop();
curr = curr -> right;
}
return res;
}
}; 中序
void fun(node){
if(!node) return;
fun(code -> left);
cout << node ->val;
fun(code -> right);
}class Solution {
public:
vector res;
vector inorderTraversal(TreeNode* root) {
stack st;
TreeNode * curr=root;
while(!st.empty() || curr){//外层while层循环表示不断读取函数参数栈中的数据
while(curr) {//内层while循环则模拟一部分的递归过程
st.push(curr);
curr=curr->left;
}
curr=st.top();
st.pop();
res.push_back(curr->val);
curr=curr->right;
}
return res;
}
}; 后序 (利用前序的变形——中右左,最后反转数组)
void fun(node){
if(!node) return;
fun(code -> left);
fun(code -> right);
cout << node ->val;
}class Solution {
public:
vector res;
vector postorderTraversal(TreeNode* root) {
TreeNode * curr = root;
stack memory;
while(!memory.empty() || curr){
while(curr){
memory.push(curr);
res.push_back(curr -> val);
curr = curr -> right;
}
curr = memory.top();
memory.pop();
curr = curr -> left;
}
reverse(res.begin(), res.end());
return res;
}
}; 缺失的第一个正数(力扣41题)
给你一个未排序的整数数组
nums,请你找出其中没有出现的最小的正整数。请你实现时间复杂度为O(n)并且只使用常数级别额外空间的解决方案。输入:nums = [1,2,0] 输出:3
难点在于不使用额外空间,并且时间常数为O(n),所以用原地哈希法。
遍历一次数组把大于等于1的和小于数组大小的值放到原数组对应位置,然后再遍历一次数组查当前下标是否和值对应,如果不对应那这个下标就是答案,否则遍历完都没出现那么答案就是数组长度加1。
class Solution {
public:
int firstMissingPositive(vector& nums) {
int len = nums.size();
for(int i = 0; i < len; i++){
while(nums[i] != i + 1){//为了将下标i处的元素,多次彻底得放到它原有的位置
if(nums[i] <= 0 || nums[i] > len || nums[i] == nums[nums[i] - 1]) break;
//分别对应着下标值小于0,大于数组长度,存在重复的情况
swap(nums[nums[i] - 1], nums[i]);
}
}
for(int i = 0; i < len; i++){
if(nums[i] != i + 1) return i + 1;
}
return len + 1;
}
}; 买卖股票的最佳时机(力扣123题)
给定一个数组,它的第
i个元素是一支给定的股票在第i天的价格。设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
输入:prices = [3,3,5,0,0,3,1,4] 输出:6
解释:在第 4 天(股票价格 = 0)的时候买入,在第 6 天(股票价格 = 3)的时候卖出,这笔交易所能获得利润 = 3-0 = 3 。随后,在第 7 天(股票价格 = 1)的时候买入,在第 8 天 (股票价格 = 4)的时候卖出,这笔交易所能获得利润 = 4-1 = 3
具体一天结束时的4种状态:
用dp[i][j][k] 表示第i天,已经发生第k次交易,手上有(j=1)或没有(j=0)股票时,所能得到的最大收益。k只能为1或2。
class Solution {
public:
int maxProfit(vector& prices) {
int n = prices.size();
vector< vector< vector > > dp = vector>>(n, vector> (2, vector(3,0)));//存储当前最大值
dp[0][1][1] = -prices[0];
dp[0][0][1] = 0;
dp[0][1][2] = -prices[0];
dp[0][0][2] = 0;
for(int i = 1; i < n; i++){
dp[i][1][1] = max(-prices[i], dp[i - 1][1][1]);
dp[i][0][1] = max(dp[i][1][1] + prices[i], dp[i - 1][0][1]);
dp[i][1][2] = max(dp[i][0][1] - prices[i], dp[i - 1][1][2]);
dp[i][0][2] = max(dp[i][1][2] + prices[i], dp[i - 1][0][2]);
}
return max(dp[n-1][0][2], dp[n - 1][0][1]);
}
}; 简化后
class Solution {
public:
int maxProfit(vector& prices) {
int n = prices.size();
vector> dp (n, vector(4));//存储当前最大值
dp[0][0] = -prices[0];
dp[0][1] = 0;
dp[0][2] = -prices[0];
dp[0][3] = 0;
for(int i = 1; i < n; i++){
dp[i][0] = max(-prices[i], dp[i - 1][0]);
dp[i][1] = max(dp[i][0] + prices[i], dp[i - 1][1]);
dp[i][2] = max(dp[i][1] - prices[i], dp[i - 1][2]);
dp[i][3] = max(dp[i][2] + prices[i], dp[i - 1][3]);
}
return max(dp[n - 1][1], dp[n - 1][3]);
}
}; 背包问题
背包问题分为完全背包和01背包,完全背包问题中,元素的个数是无限的,01背包中,元素的个数是有限的。一般的解法都是维护一个一维数组,然后用两层for循环遍历,一层for循环遍历别抱容量,一层for循环遍历元素数组,具体的哪一层在外面,以及用正序还是倒序,根据不同的问题来定。
01背包中一维dp数组的两个for循环内外循序一定是先遍 历物品,再遍历背包容量注意:内层循环(背包容量)必须倒序遍历,保证每个物品只取一次。
在完全背包中,对于一维dp数组来说,其实两个for循环嵌套顺序同样无所谓(仅限于纯完全背包问
题! ),如果是要求组合,不允许重复的话,外层遍历元素数组,内层遍历容量。
参考文章
01背包:力扣416题
分割等和子集:判断是否能将一个数组分割为两个子集,其和相等
0-1背包存在性问题:是否存在一个子集,其和为target=sum/2,外循环nums,内循环target倒序
bool canPartition(vector &nums)
{
int sum = accumulate(nums.begin(), nums.end(), 0);
if (sum % 2 == 1) //如果是和为奇数显然无法分成两个等和子集
return false;
int target = sum / 2;
vector dp(target + 1, 0); //dp[i]:是否存在子集和为i
dp[0] = true; //初始化:target=0不需要选择任何元素,所以是可以实现的
for (int num : nums)
for (int i = target; i >= num; i--)
dp[i] = dp[i] || dp[i - num];
return dp[target];
} 完全背包:力扣518题
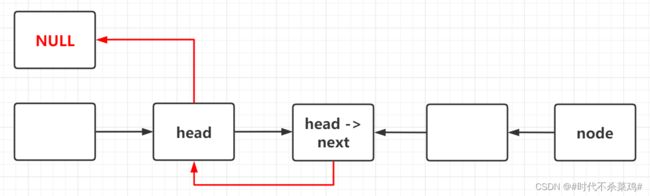
反转链表的递归
class Solution {
public:
ListNode* reverseList(ListNode* head) {
if(!head || !head -> next) return head;
ListNode * node = reverseList(head -> next);
head -> next -> next = head;
head -> next = nullptr;
return node;
}
};合并链表的递归
ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
if(!list1) return list2;
if(!list2) return list1;
if(list1 -> val > list2 -> val){
list2 -> next = mergeTwoLists(list1, list2 -> next);
return list2;
}
list1 -> next = mergeTwoLists(list1 -> next, list2);
return list1;
} 回溯法
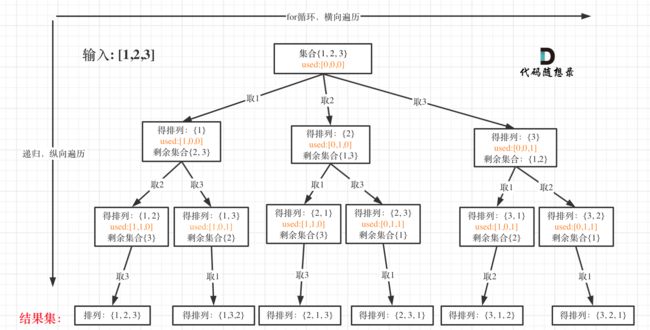
全排列(力扣46)
给定一个不含重复数字的数组 nums ,返回其所有可能的全排列 。你可以 按任意顺序返回答案。
示例 1:输入:nums = [1,2,3] 输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
class Solution {
public:
vector> res;
vector temp;
vector used;
vector> permute(vector& nums) {
used = vector (nums.size(), false);
dfs(nums);
return res;
}
void dfs(vector& nums){
if(temp.size() == nums.size()) {
res.push_back(temp);
return;
}
for(int i = 0; i < nums.size(); i++){
if(used[i]) continue;
used[i] = true;
temp.push_back(nums[i]);
dfs(nums);
temp.pop_back();
used[i] = false;
}
}
}; 全排列-Ⅱ(力扣47题)
给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。
示例 1:输入:nums = [1,1,2] 输出:[[1,1,2], [1,2,1], [2,1,1]]
class Solution {
public:
vector> res;
vector used;
vector temp;
vector> permuteUnique(vector& nums) {
used = vector (nums.size(), false);
sort(nums.begin(), nums.end());
dfs(nums);
return res;
}
void dfs(vector & nums){
if(temp.size() == nums.size()){
res.push_back(temp);
return;
}
for(int i = 0; i < nums.size(); i++){
if(used[i]) continue;//处于同一个树枝上,已经被访问过
if(i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) continue;//处于同一层
used[i] = true;
temp.push_back(nums[i]);
dfs(nums);
temp.pop_back();
used[i] = false;
}
}
}; 数组的全排列等回溯问题,需要用到used数组,来记录数组中的元素的访问情况。used一开始初始化元素都为false。
在后续的遍历中,如果used[i] == true 表示nums[i]已经被访问过,如果nums[i] == nums[i - 1] && !used[i - 1],表示nums[i - 1]与nums[i] 在同一层,且已经被访问过。(描述可能不太准确,结合代码理解。)
全排列Ⅲ-字符串全排列(剑指37)
输入一个字符串,打印出该字符串中字符的所有排列。
你可以以任意顺序返回这个字符串数组,但里面不能有重复元素。
示例: 输入:s = "abc" 输出:["abc","acb","bac","bca","cab","cba"]
class Solution {
public:
vector res;
string temp;
vector used;
vector permutation(string s) {
used = vector(s.length(), false);
sort(s.begin(), s.end());
dfs(s);
return res;
}
void dfs(string & s){
if(temp.length() == s.length()){
res.push_back(temp);
return;
}
for(int i = 0; i < s.length(); i++){
if(used[i]) continue;
if(i > 0 && s[i] == s[i - 1] && !used[i - 1]) continue;
temp.push_back(s[i]);
used[i] = true;
dfs(s);
temp.pop_back();
used[i] = false;
}
}
}; 子集(力扣78题)
给你一个整数数组
nums,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
输入:nums = [1,2,3] 输出:[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
class Solution {
public:
vector temp;
vector> res;
vector> subsets(vector& nums) {
dfs(nums, 0);
res.push_back({});
return res;
}
void dfs(vector & nums, int index){
if(index == nums.size()) return;
for(int i = index; i < nums.size(); i++){
temp.push_back(nums[i]);
res.push_back(temp);
dfs(nums, i + 1);
temp.pop_back();
}
}
}; 子集Ⅱ(力扣90题)
给你一个整数数组 nums ,其中可能包含重复元素,请你返回该数组所有可能的子集(幂集)。解集 不能 包含重复的子集。返回的解集中,子集可以按 任意顺序 排列。
输入:nums = [1,2,2] 输出:[[],[1],[1,2],[1,2,2],[2],[2,2]]
class Solution {
public:
vector temp;
vector used;
vector> res;
vector> subsetsWithDup(vector& nums) {
used = vector (nums.size(), false);
sort(nums.begin(), nums.end());
dfs(nums, 0);
res.push_back({});
return res;
}
void dfs(vector & nums, int index){
if(index == nums.size()) return;
for(int i = index; i < nums.size(); i++){
if(i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) continue;
temp.push_back(nums[i]);
res.push_back(temp);
used[i] = true;
dfs(nums, i + 1);
used[i] = false;
temp.pop_back();
}
}
}; 组合总和(力扣39题)
给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。
candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。
输入:candidates = [2,3,6,7], target = 7 输出:[[2,2,3],[7]]
class Solution {
public:
int targetnum;
vector temp;
vector> res;
vector> combinationSum(vector& candidates, int target) {
targetnum = target;
dfs(candidates, 0, 0);
return res;
}
void dfs(vector& candidates, int sum, int index){
if(sum > targetnum) return;
if(sum == targetnum) {
res.push_back(temp);
return;
}
for(int i = index; i < candidates.size(); i++){
temp.push_back(candidates[i]);
dfs(candidates, sum + candidates[i], i);
temp.pop_back();
}
}
}; 组合总和Ⅱ(力扣40)
给定一个候选人编号的集合 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用 一次 。
注意:解集不能包含重复的组合。
示例 1: 输入: candidates = [10,1,2,7,6,1,5], target = 8,
输出:[ [1,1,6], [1,2,5], [1,7], [2,6] ]
class Solution {
public:
vector> res;
vector temp;
vector used;
int my_target;
vector> combinationSum2(vector& candidates, int target) {
sort(candidates.begin(), candidates.end());
used = vector (candidates.size(), false);
my_target = target;
dfs(candidates, 0, 0);
return res;
}
void dfs(vector& candidates, int sum, int index){
if(sum >= my_target){
if(sum == my_target) res.push_back(temp);
return;
}
for(int i = index; i < candidates.size(); i++){
if(i > 0 && candidates[i] == candidates[i - 1] && !used[i - 1]) continue;
temp.push_back(candidates[i]);
used[i] = true;
dfs(candidates, sum + candidates[i], i + 1);
temp.pop_back();
used[i] = false;
}
}
}; 验证二叉搜索树(力扣98)
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
中序遍历 维护两个节点 pre 与 root ,表示中序遍历过程中,一前一后两个节点,他们的大小也应该是确定的一大一小
class Solution {
public:
TreeNode * pre = NULL;
bool isValidBST(TreeNode* root) {
if(!root) return true;
bool b1 = isValidBST(root -> left);
if(pre && pre -> val >= root -> val) return false;
pre = root;
bool b2 = isValidBST(root -> right);
return b1 && b2;
}
};最小路径和(力扣第64题)
给定一个包含非负整数的 m x n 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。说明:每次只能向下或者向右移动一步。
思路一: 深度优先遍历 想法没有错 但是在遍历一些较大的二维数组时,会发生超时
class Solution {
public:
vector> vec;
int res, m, n;
int minPathSum(vector>& grid) {
res = INT_MAX;
vec = grid;
m = grid.size();
n = grid[0].size();
dfs(0, 0, 0);
return res;
}
void dfs(int i, int j, int sum){
if(i >= m || j >= n) {
if(i == m - 1 || j == n - 1)
res = min(res, sum);
return;
}
dfs(i + 1, j, sum + vec[i][j]);
dfs(i, j + 1, sum + vec[i][j]);
}
}; 思路二:动态规划法
class Solution {
public:
int minPathSum(vector>& grid) {
int m = grid.size();
int n = grid[0].size();
vector> dp(m, vector(n, 0));
dp[0][0] = grid[0][0];
for(int i = 1; i < m; i++) dp[i][0] = dp[i - 1][0] + grid[i][0];
for(int j = 1; j < n; j++) dp[0][j] = dp[0][j - 1] + grid[0][j];
for(int i = 1; i < m; i++){
for(int j = 1; j < n; j++){
dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];
}
}
return dp[m - 1][n - 1];
}
}; 扩展: 要求打印最小路径
需要再建立一个二维数组,每个位置标记1或2,记录当前的最小路径是从上还是从左转移过来的,最后倒推
动态规划之最小串(力扣718,1143题)
最长重复子数组
给两个整数数组 nums1 和 nums2 ,返回 两个数组中 公共的 、长度最长的子数组的长度 。
输入:nums1 = [1,2,3,2,1], nums2 = [3,2,1,4,7] 输出:3
解释:长度最长的公共子数组是 [3,2,1] 。
关键:将dp[i][j]设置为长度为i,末尾项为num1[i-1]的子数组,与长度为j,末尾项为nums2[j-1]的子数组,二者的最大公共后缀子数组长度,即dp[i][j]下两个数组的nums1[i - 1] 与 nums2[j - 1]元素是一定包含的,那么状态转移方程就可以分成两种情况:nums1[i - 1] == nums2[j - 1] 与 nums1[i - 1] != nums2[j - 1]
class Solution {
public:
int findLength(vector& nums1, vector& nums2) {
int len1 = nums1.size(), len2 = nums2.size(), res = 0;
vector> dp(len1 + 1, vector(len2 + 1, 0));
for(int i = 1; i <= len1; i++){
for(int j = 1; j <= len2; j++){
if(nums1[i - 1] == nums2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + 1;
res = max(res, dp[i][j]);
}
}
}
return res;
}
}; 最长公共子序列
给定两个字符串 text1 和 text2,返回这两个字符串的最长公共子序列的长度。如果不存在 公共子序列 ,返回 0 。
一个字符串的子序列是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
例如,"ace" 是 "abcde" 的子序列,但 "aec" 不是 "abcde" 的子序列。
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。输入:text1 = "abcde", text2 = "ace" 输出:3
解释:最长公共子序列是 "ace" ,它的长度为 3 。
此题与上一题不同的是,此题的公共子串可以是不连续的,那么当 text1[i - 1] != text2[j - 1]时,
dp[i][j] 不一定为0,它应该取已经遍历过的子串中的最大值,即max(dp[i][j - 1], dp[i - 1][j])
注意: 在做这种子串题时,二维动态数组dp[i][j]的实际意义应该从两个字符串的公共串来考虑(或者说多考虑考虑字符串text1以 text1[i - 1]结尾的子串和字符串text2以text2[j - 1]结尾的子串之间的关系,不要过分纠结于二维数组本身的转换与意义)
class Solution {
public:
int longestCommonSubsequence(string text1, string text2) {
int len1 = text1.length(), len2 = text2.length(), res = 0;
vector> dp(len1 + 1, vector(len2 + 1, 0));
for(int i = 1; i <= len1; i++){
for(int j = 1; j <= len2; j++){
if(text1[i - 1] == text2[j -1]){
dp[i][j] = dp[i - 1][j - 1] + 1;
}
else{
dp[i][j] = max(dp[i][j - 1], dp[i - 1][j]);
}
res = max(res, dp[i][j]);
}
}
return res;
}
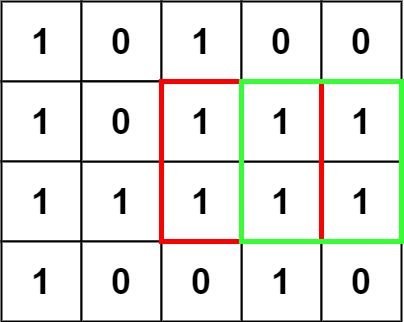
}; 与最小串动态规划思路相似的题——最大正方形(力扣221)
在一个由 '0' 和 '1' 组成的二维矩阵内,找到只包含 '1' 的最大正方形,并返回其面积。
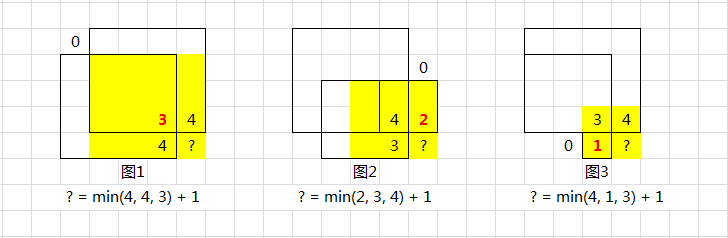
与上面的思路类似,创建一个二维数组dp[][],dp[i][j]表示以matrix[i][j]点为右下角的矩阵的最大值。dp[i][j]都是用来表示某个数据结构的结尾情况。
当matrix[i][j]=0时,dp[i][j]直接为0;当matrix[i][j]=1时,dp[i][j]为dp[i-1][j], dp[i-1][j-1],dp[i][j-1]三者最小值加1;
class Solution {
public:
int maximalSquare(vector>& matrix) {
int res = 0, len1 = matrix.size(), len2 = matrix[0].size();
vector> dp(len1 + 1, vector(len2 + 1, 0));
for(int i = 1; i <= len1; i++){
for(int j = 1; j <= len2; j++){
if(matrix[i - 1][j - 1] == '1') {
dp[i][j] = min({dp[i - 1][j], dp[i][j - 1], dp[i - 1][j - 1]}) + 1;
}
res = max(dp[i][j], res);
}
}
return pow(res, 2);
}
}; 岛屿问题
岛屿数量(力扣200题)
给一个由 '1'(陆地)和 '0'(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。假设该网格的四条边均被水包围。
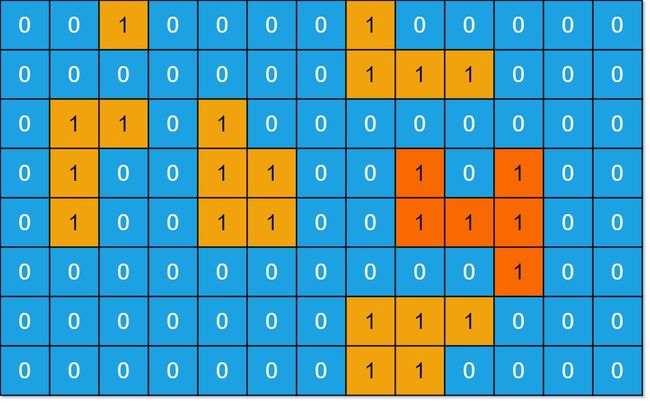
输入:
输出:6
岛屿问题中,这些岛屿的形状是不规则的,如L型,而不是矩形或者正方形,所以不能用动态规划法来做。考虑用dfs,两层for循环遍历grid数组,当遇到值为1的元素,就执行dfs函数。dfs函数在执行的过程中,将遍历过的元素都置为0。
class Solution {
public:
int numIslands(vector>& grid) {
int res = 0;
for(int i = 0; i < grid.size(); i++){
for(int j = 0; j < grid[0].size(); j++){
if(grid[i][j] == '1') {
dfs(grid, i, j);
res++;
}
}
}
return res;
}
void dfs(vector>& grid, int i, int j){
if(i < 0 || j < 0 || i == grid.size() || j == grid[0].size() || grid[i][j] == '0') return;
grid[i][j] = '0';
dfs(grid, i, j - 1);
dfs(grid, i, j + 1);
dfs(grid, i - 1, j);
dfs(grid, i + 1, j);
}
}; 岛屿最大面积(力扣695)
求上题存在的岛屿中,面积的最大者,解法类似,不过需要新增一个全局变量area,每次进入dfs之前置0,dfs执行完之后,用它来更新最大值。
class Solution {
public:
int area;
int maxAreaOfIsland(vector>& grid) {
int res = 0;
for(int i = 0; i < grid.size(); i++){
for(int j = 0; j < grid[0].size(); j++){
if(grid[i][j] == 1){
area = 0;
fun(grid, i, j);
res = max(res, area);
}
}
}
return res;
}
void fun(vector>& grid, int i, int j){
if(i < 0 || j < 0 || i == grid.size() || j == grid[0].size() || grid[i][j] == 0) return;
area++;
grid[i][j] = 0;
fun(grid, i, j - 1);
fun(grid, i, j + 1);
fun(grid, i - 1, j);
fun(grid, i + 1, j);
}
}; 单调栈问题
单调栈通常用来解决 下一个更大数或下一个更小数 的问题,如果要求的是下一个更大的数,则构造由栈底到栈顶递增的单调栈,反之则构造由栈底到栈顶递减的单调栈。每次有数据入栈时,有两个选择:将栈顶元素弹出栈或直接将元素放入栈,如果是前者则更新栈顶元素的下一个更大值(更小值)。当数组中的元素全都入栈完毕后,如果栈中仍然存在元素,那么这些元素则没有下一个更大值(更小值)。
496. 下一个更大元素 I
nums1中数字x的 下一个更大元素 是指x在nums2中对应位置 右侧 的 第一个 比x大的元素。给你两个 没有重复元素 的数组nums1和nums2,下标从 0 开始计数,其中nums1是nums2的子集。对于每个
0 <= i < nums1.length,找出满足nums1[i] == nums2[j]的下标j,并且在nums2确定nums2[j]的 下一个更大元素 。如果不存在下一个更大元素,那么本次查询的答案是-1。返回一个长度为nums1.length的数组ans作为答案,满足ans[i]是如上所述的 下一个更大元素 。输入:nums1 = [4,1,2], nums2 = [1,3,4,2]. 输出:[-1,3,-1]
class Solution {
public:
vector nextGreaterElement(vector& nums1, vector& nums2) {
stack temp;//栈单调减
map exam;
int len=nums2.size();
for(int i=0;i 84. 柱状图中最大的矩形
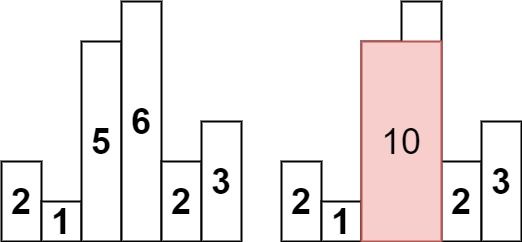
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
class Solution {
public:
int largestRectangleArea(vector& heights) {
stack memory;//构建单调栈 单调增
heights.insert(heights.begin(), 0);
memory.push(0);
int len = heights.size(), l = 0, h = 0, res = 0;
for(int i = 1; i < len; i++){
while(heights[i] < heights[memory.top()]){
h = heights[memory.top()];
memory.pop();
l = i - memory.top() - 1;
res = max(res, l * h);
}
memory.push(i);
}
while(memory.top() != 0){
h = heights[memory.top()];
memory.pop();
l = len - memory.top() - 1;
res = max(res, l * h);
}
return res;
}
}; 背包问题
背包问题分为01背包问题和完全背包问题
对于完全背包问题:
如果求组合数(对于元素的顺序没有要求),就是外层for循环遍历物品,内层for遍历背包。
如果求排列数(对于元素的顺序有要求),就是外层for遍历背包,内层for循环遍历物品。
对于01背包问题:
外层for循环遍历物品,内层for循环倒序遍历背包
组合问题公式
dp[i] += dp[i-num]True、False问题公式
dp[i] = dp[i] || dp[i-num]最大最小问题公式
dp[i] = min(dp[i], dp[i-num]+1)或者dp[i] = max(dp[i], dp[i-num]+1)1、组合问题:
377. 组合总和 Ⅳ
494. 目标和
518. 零钱兑换 II
2、True、False问题:
139. 单词拆分
416. 分割等和子集
3、最大最小问题:
474. 一和零
322. 零钱兑换
最长公共子串和最长公共子序列
最长公共子串(连续的)
给定两个字符串str1和str2,输出两个字符串的最长公共子串题目保证str1和str2的最长公共子串存在且唯一。
class Solution {
public:
string LCS(string str1, string str2) {
int len1 = str1.length(), len2 = str2.length();
vector> dp(len1 + 1, vector(len2 + 1, 0));
int begin = 0, len = 0;
for(int i = 1; i <= len1; i++){
for(int j = 1; j <= len2; j++){
if(str1[i - 1] == str2[j - 1]){
dp[i][j] = dp[i - 1][j - 1] + 1;
if(dp[i][j] > len){
len = dp[i][j];
begin = i - len;
}
}
}
}
return str1.substr(begin, len);
}
}; 最长公共子序列(不连续)
给定两个字符串text1和text2,返回这两个字符串的最长公共子序列 的长度。如果不存在公共子序列,返回0。
class Solution {
public:
int longestCommonSubsequence(string text1, string text2) {
int m = text1.length(), n = text2.length();
vector> dp(m + 1, vector(n + 1, 0));
for(int i = 1; i <= m; i++){
for(int j = 1; j <= n; j++){
if(text1[i - 1] == text2[j - 1]){
dp[i][j] = 1 + dp[i - 1][j - 1];
}
else dp[i][j] = max({dp[i - 1][j], dp[i][j - 1], dp[i - 1][j - 1]});
}
}
return dp[m][n];
}
};