C++二叉树进阶——二叉搜索树
目录
1 二叉搜索树
1.1 二叉搜索树概念
1.2 二叉搜索树操作
1.2.1 二叉搜索树的查找
1.2.2 二叉搜索树的插入
1.2.3 二叉树的删除
1.3 二叉树的实现
1.4 二叉搜索树的应用
1 二叉搜索树
1.1 二叉搜索树概念
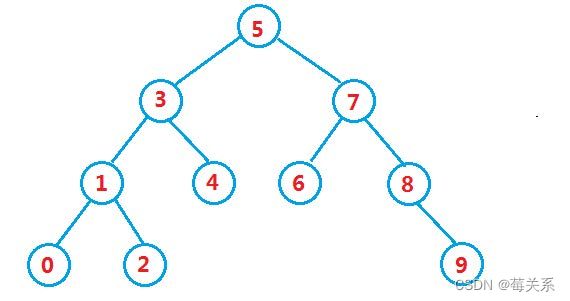
二叉搜索树又称二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树:
若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
它的左右子树也分别为二叉搜索树
int a [] = {5,3,4,1,7,8,2,6,0,9};
1.2 二叉搜索树操作
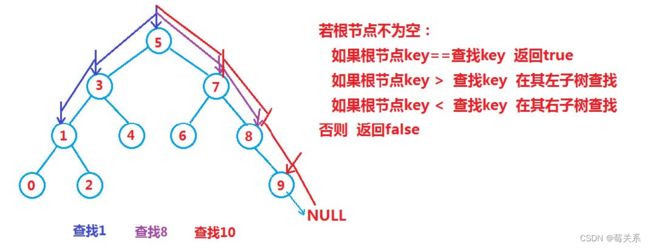
1.2.1 二叉搜索树的查找
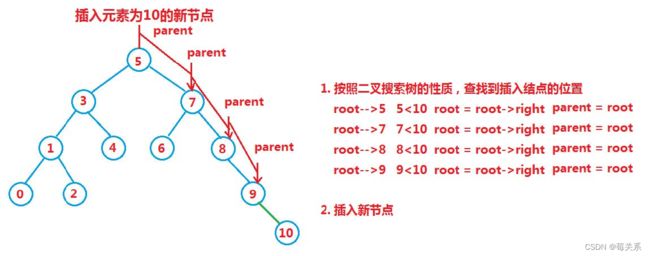
1.2.2 二叉搜索树的插入
插入的具体过程如下
a.树为空,则直接插入
b.树不空,按二叉搜索树性质查找插入位置,插入新节点
1.2.3 二叉树的删除
二叉树的删除是二叉搜索树里最难的一个部分
首先查找元素是否在二叉搜索树中,如果不存在,则返回, 否则要删除的结点分为两种情况
a.要删除结点最多只有一个子结点(要么没有子结点,要么只有左子结点或右子结点)
b.要删除结点既有左子结点,又有右子结点
首先第一种情况
要删除结点最多只有一个子结点
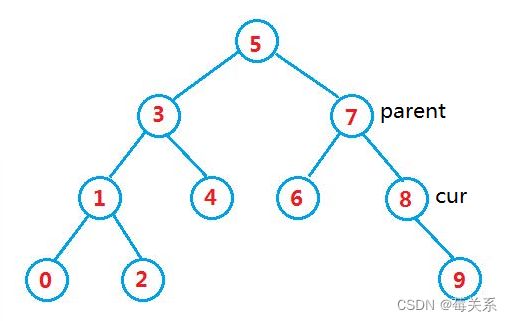
如图所示,结点6和结点8分别是,没有子结点和只有一个子结点的情况。
以结点8为例,定义一个cur用来找到结点8,同时顶一个parent用来记录cur的父结点。找到结点8的时候,结点8的父结点也能被我们记录着。
这是分情况对结点8进行讨论。
1、cur是parent的左结点
a. cur的子结点是左孩子 parent->left = cur->left;
b.cur的子结点是右孩子 parent->left = cur->right;
2、cur是parent的右结点
a. cur的子结点是左孩子 parent->right = cur->left;
b.cur的子结点是右孩子 parent->right = cur->right;
cur没有孩子结点一样可以使用上面的情况,因为无论是cur->left还是cur->right都是空,直接赋值给parent的左结点或者是右结点。
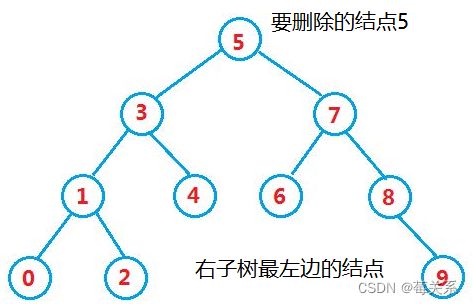
要删除的结点既有左孩子结点,又有右孩子结点
以结点5为例,要想删除结点5,用其他的结点来替换。该结点左子树最右边的结点或者是右子树最左边的结点。
找到要删除的结点5之后,接下来开始寻找右子树中最左边的结点,结点6(这个最左边的结点是一定没有左子树的)。
如图所示
接下来就是让结点6去替换结点5,然后把结点5删除掉。
要把替换之后的结点5删掉,需要找到结点5的父结点,也就是结点7。
所以我们在找到右子树中最左边的结点的时候,同时还需要记录该结点的父结点。
PNode min = cur->_right;
PNode minparent = cur;
while (min->_left)
{
minparent = min;
min = min->_left;
}
swap(cur->_data, min->_data);然后结点5变成了最多只有一个子结点的情况。判断结点5是父结点7的左结点还是右结点。
if (min == minparent->_left)
{
minparent->_left = min->_right;
}
else
{
minparent->_right = min->_right;
}这样就完成了,搜索二叉树的删除。
1.3 二叉树的实现
#include
#include
#include
using namespace std;
template
struct BSTNode
{
BSTNode(const T data = T(),const V value = V())
:_data(data)
,_value(value)
,_left(nullptr)
,_right(nullptr)
{}
BSTNode* _left;
BSTNode* _right;
T _data;
V _value;
};
template
class BSTree
{
public:
typedef BSTNode Node;
typedef Node* PNode;
BSTree()
:_root(nullptr)
{}
Node* Find(const T key)
{
if (_root == nullptr)
{
return nullptr;
}
PNode cur = _root;
while (cur)
{
if (cur->_data > key)
{
cur = cur->_left;
}
else if (cur->_data < key)
{
cur = cur->_right;
}
else
{
//cout << cur->_data << endl;
return cur;
}
}
return nullptr;
}
bool Insert(const T& data,const V& value)
{
if (_root == nullptr)
{
_root = new Node(data,value);
return true;
}
PNode parent = nullptr;
PNode cur = _root;
while (cur)
{
if (cur->_data > data)
{
parent = cur;
cur = cur->_left;
}
else if(cur->_data < data)
{
parent = cur;
cur = cur->_right;
}
else
{
return false;
}
}
cur = new Node(data, value);
if (data > parent->_data)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
return true;
}
void InOrder()
{
_InOrder(_root);
cout << endl;
}
bool Erase(const T& data)
{
//首先找到要删除数字的位置
if (_root == nullptr)
{
return false;
}
PNode cur = _root;
PNode parent = nullptr;
while (cur)
{
if (cur->_data > data)
{
parent = cur;
cur = cur->_left;
}
else if (cur->_data < data)
{
parent = cur;
cur = cur->_right;
}
else
{
//要删除的结点无孩子结点
//要删除的结点只有左孩子结点
//要删除的结点只有右孩子结点
if (cur->_left == nullptr)
{
if (parent == nullptr)
{
_root = cur->_right;
break;
}
if (cur == parent->_left)
{
parent->_left = cur->_right;
}
else
{
parent->_right = cur->_right;
}
}
else if(cur->_right == nullptr)
{
if (parent == nullptr)
{
_root = cur->_left;
break;
}
if (cur == parent->_left)
{
parent->_left = cur->_left;
}
else
{
parent->_right = cur->_left;
}
}
else
{
//要删除的结点有左、右孩子结点
PNode min = cur->_right;
PNode minparent = cur;
while (min->_left)
{
minparent = min;
min = min->_left;
}
swap(cur->_data, min->_data);
if (min == minparent->_left)
{
minparent->_left = min->_right;
}
else
{
minparent->_right = min->_right;
}
cur = min;
}
break;
}
}
delete cur;
return false;
}
private:
PNode _root;
void _InOrder(PNode root)
{
if (root == nullptr)
{
return;
}
_InOrder(root->_left);
cout << root->_data << ' ' << root->_value << endl;
_InOrder(root->_right);
}
};
int main()
{
//BSTree dict;
//dict.Insert("insert", "插入");
//dict.Insert("erase", "删除");
//dict.Insert("left", "左边");
//dict.Insert("string", "字符串");
//string str;
//while (cin >> str)
//{
// auto ret = dict.Find(str);
// if (ret)
// {
// cout << str << ":" << ret->_value << endl;
// }
// else
// {
// cout << "单词拼写错误" << endl;
// }
//}
string strs[] = { "苹果", "西瓜", "苹果", "樱桃", "苹果", "樱桃", "苹果", "樱桃", "苹果" };
// 统计水果出现的次
BSTree countTree;
for (auto str : strs)
{
auto ret = countTree.Find(str);
if (ret == NULL)
{
countTree.Insert(str, 1);
}
else
{
ret->_value++;
}
}
countTree.InOrder();
return 0;
} 1.4 二叉搜索树的应用
1、K模型:K模型即只有key作为关键码,结构中只需要存储Key即可,关键码即为需要搜索到的值。
比如:给一个单词word,判断该单词是否拼写正确,具体方式如下:
以单词集合中的每个单词作为key,构建一棵二叉搜索树
在二叉搜索树中检索该单词是否存在,存在则拼写正确,不存在则拼写错误。
2、KV模型:每一个关键码key,都有与之对应的值Value,即
<单词,中文含义>为键值对构造二叉搜索树,注意:二叉搜索树需要比较,键值对比较时只比较
Key
查询英文单词时,只需给出英文单词,就可快速找到与其对应的key。