量化选股——基于动量因子的行业风格轮动策略(第1部分—因子测算)
文章目录
- 动量因子与行业轮动概述
-
- 动量因子的理解
- 投资视角下的行业轮动现象
- 投资者视角与奈特不确定性
- 动量因子在行业风格上的效果测算
-
- 动量因子效果测算流程概述
- 1. 行业选择:申万一级行业
- 2. 动量因子选择:阿隆指标(Aroon)
- 3. 测算方法
-
- 1.选择特定的时间区间
- 2.计算阿隆指标(Arron)
- 3. 统计收益率&胜率
- 4. 测算结论
【量化选股——基于动量因子的行业风格轮动策略】分为两部分:
- 第1部分—因子测算
- 第2部分—策略回测
动量因子与行业轮动概述
动量因子的理解
动量,可以理解为“势头”,“强势的程度”。汽车遇到红灯时,不是一下子停下,而是滑行一段再停。滑行的这一段就解释为“动量”造成的。动量因子表示,即便情况发生了变化,这些因子所代表的势头仍会持续一段时间。
动量因子一直饱受争议,因为它的前提假设是股票会表现出马太效应。意思是:股票的相对强弱趋势会延续,并且表现出“强者恒强,弱者恒弱”的态势,除非有意外情况发生才会导致强弱之势逆转。动量因子表现出两种效应:
- 动量效应:股票的收益率会延续
- 反转效应:经过较长时间后,收益会翻转
挖掘动量因子的过程往往是先算出结果,再找一个逻辑来解释。因此动量因子其实没有太多的基础理论支撑,是在实践中被摸索出来的。使用动量因子的风险也很高,因为对动量因子的解释性的逻辑往往超脱了我们过去所知的对市场理解的框架体系,有一种“唯数据论”的感觉。这里博主希望大家能够辩证的看待动量因子,有自己的看法。
通常学界对动量因子的理解有以下几种:
-
投资者的决策行为,导致了动量因子的产生。如中国人个人炒股比例高,而且由于缺乏背景知识,缺乏对基本面的了解,同时好大喜功求快,导致短线操作居多,跟风者居多;
但反对者认为这种猜测无法定量评估,而这样的解释是“为了发展一个理论模型而寻找不合理的逻辑假设”
-
因为每个市场的参与者,接收同一个信息的时间都不同,因此即便某个事件发生了,依旧会因为接收信息的时间差导致参与者在操作上存在时间差,所以时间差导致了动量这种“效应”的产生。同样,也可能因为存在一些信息差,不对称的信息差会随着时间流逝慢慢对称,这个过程也会造成动量。
但反对者同样认为:既然存在操作的时间差,那么利好和利空的消息都应该存在时间差,而往往动量因子只能体现出某一边的动量。(如,某些代表利好的动量因子无法解释利空的情况;或者说,动量因子本身就不应该被分为利好或利空,否则就代表它只验证了对一边有效)
-
市场的参与者都有自己入场的动机与离场的目的,不同参与者也是在市场中不断博弈与进化的(市场具有“奈特不确定性”)。按照书本所述,股票现在合理的价格,就是对未来现金流的折现。那么不同的参与者因为伴随有不同的入场与离场的目的,因此站在各自的立场上,对“未来现金流折现”的估值也不同,而这种行为伴随着市场的进化与发展,导致“动量”作为一个观测现象而产生。
这就意味着“动量”是一种表面现象,它不是因为固定的几个逻辑直接导致的结果,而是博弈造成的一种被观测出来的现象。
目前动量因子在个股上是作为多因子模型的一部分存在,而如果将视野扩大到行业层面,就可以单独拿动量因子进行建模测算,此时因子的动量效应较为明显。通常认为是因为暴露的因子动量会随着个股传递到整个行业组合上,因此观测较为明显。
我们常见的动量因子通常包含:
- 过去一段时间(1周、10天、一个月、3个月)的收益率
- 5、10、20、30、60天收盘价均线
- 过去一段时间板块、行业的高开低收等数据
投资视角下的行业轮动现象
我们以接收信息的时间差导致参与者在操作上存在时间差,所以时间差导致了动量这种“效应”的产生为视角,就可以发现在行情走势上:
-
市场上有大量未接受到该信息的投资者:标的买卖双方造成的买卖供需关系并不会显著到立即把价格推向其应当达到的位置,此时表现在信息的“反应不足”
-
越来越多的投资者接触到了该信息并做出反应:此时价格逐渐被推至合理价格附近,但后入市场的投资者中有一部分因为各种各样的原因,错误或过分估计了该信息价值,从而将该股票价格再进一步推离了合理价格,此时“反应过度”,出现超买、超卖现象
-
超买超卖现象被发现:市场的投资者捕捉到反映过度带来的盈利空间,通过交易获取超额收益的同时,将股票价格再度往合理价格处推动。

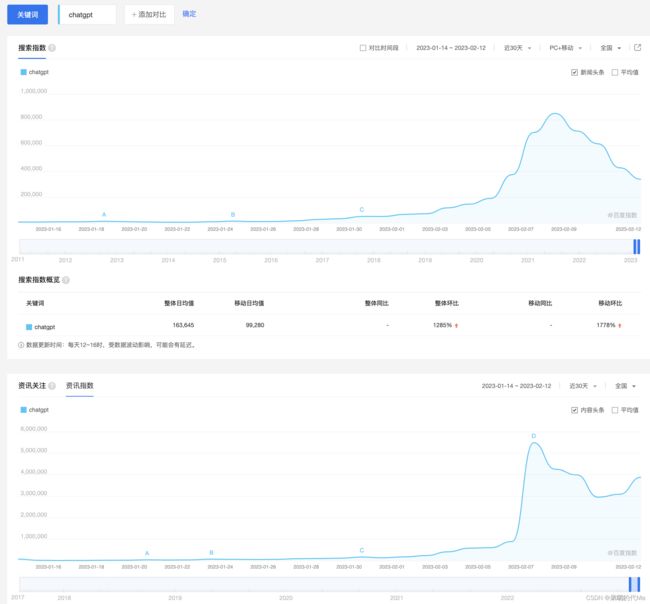
比如:在2022年11月30日ChatGPT就已经向公众开放:
- 11月30日OpenAI(ChatGPT的作者)在维基百科发布关于ChatGPT的百科信息
- 12月6日开始维基百科词条开始普通用户参与修改,并且参与修改的用户账号量每日增长显著
- 12月新闻既有“小学生击败ChatGPT”,“差点被ChatGPT骗了”,“举一千反一,人类离xxx还有多远”等负面看法,也有“爆火的ChatGPT太强了”等正面观点

复盘12、1、2月份到如今的ChatGPT概念(BK1126),可以发现站在投资者的视角上:
- 投资者无法判断信息是从何时开始反映在市场上的,也无法判断未来将持续多长时间
- 投资者难以评估信息的市场价值,信息带来的对预期的影响,能造成的股价涨跌幅难以度量
- 信息源种类、观点、立场繁多,难以主观评价
如今,百度指数上,ChatGpt的搜索指数与资讯关注度依旧很高,但相对高点已经走弱,由于是境外资讯,而百度搜索面向国内用户,因此国内资讯会优先与国内的搜索指数呈现出增长的趋势
因此在行业轮动上,动量指标盈利的来源:
- 市场上有大量未接受到该信息的投资者
- 越来越多的投资者接触到了该信息并做出反应(动量指标盈利主因)
- 超买超卖现象被发现(动量指标亏损主因)
投资者视角与奈特不确定性
奈特把对未来的不确定性分为两种,一种称为“风险”,另一种称为“奈特不确定性”,将未知分为了两类:
- 风险:具有特定概率分布的不确定性
- 奈特不确定性:没有特定概率分布的不确定性
后续的研究证明:
- 人们常对奈特不确定性表现出厌恶的倾向,并愿意为避免奈特不确定性而支付溢价
- 厌恶奈特不确定性的人不一定厌恶风险,即“赌鬼也讨厌奈特不确定”
- 在人们面临奈特不确定性时,会出现群体盲从的现象,形成羊群效应,此时人们更在乎别人的想法
当信息被越来越多的人接触到的时候,投资者面临的其实就不是完全未知的“奈特不确定性”,而是可以评估盈利与亏损区间与概率的“风险”了。但相对的,不同的市场参与者对信息的敏感程度与评估是不同的,从这个角度也验证了上述的第二条:“投资者难以评估信息的市场价值,信息带来的对预期的影响,能造成的股价涨跌幅难以度量”。对于信息的动量与价格走势趋势的判断需要策略研究员进行细致的研究。
动量因子在行业风格上的效果测算
动量因子效果测算流程概述
- 首先我们选择“申万一级”行业指数,阿隆指标(Aroon)作为动量指标进行测算
- 然后根据指数数据集,选择公共的时间段(2015-01-01 至 2023-01-01)将日期分为两个部分:
- 选择 2015-01-01 至 2020-01-01 这一段时期进行测算
- 选择 2020-01-01 至 2023-01-01 这一段时期进行回测
- 选择测算的时间段进行测算
- 选择回测的时间段进行回测
1. 行业选择:申万一级行业
我们选取申万一级行业指数来测算
申万行业分类规则请参考:申万行业分类标准(2021版)
| 行业代码 | 行业名称 | 成份个数 | 静态市盈率 | TTM(滚动)市盈率 | 市净率 | 静态股息率 | |
|---|---|---|---|---|---|---|---|
| 0 | 801010.SI | 农林牧渔 | 99 | 47.13 | 47.64 | 2.84 | 0.62 |
| 1 | 801030.SI | 基础化工 | 343 | 15.92 | 15.02 | 2.48 | 2.11 |
| 2 | 801040.SI | 钢铁 | 44 | 7.27 | 12.03 | 1.06 | 5.65 |
| 3 | 801050.SI | 有色金属 | 128 | 24.55 | 15.51 | 2.69 | 1.21 |
| 4 | 801080.SI | 电子 | 308 | 23.88 | 27.29 | 2.94 | 1.21 |
| 5 | 801880.SI | 汽车 | 240 | 29.28 | 28.17 | 2.27 | 1.31 |
| 6 | 801110.SI | 家用电器 | 79 | 17.60 | 16.00 | 2.82 | 2.97 |
| 7 | 801120.SI | 食品饮料 | 119 | 40.73 | 36.84 | 7.84 | 1.77 |
| 8 | 801130.SI | 纺织服饰 | 113 | 16.82 | 17.74 | 1.97 | 3.48 |
| 9 | 801140.SI | 轻工制造 | 148 | 21.67 | 25.74 | 2.38 | 1.81 |
| 10 | 801150.SI | 医药生物 | 360 | 29.34 | 26.32 | 3.57 | 1.08 |
| 11 | 801160.SI | 公用事业 | 123 | 21.32 | 19.21 | 1.90 | 2.28 |
| 12 | 801170.SI | 交通运输 | 124 | 9.87 | 8.48 | 1.28 | 4.62 |
| 13 | 801180.SI | 房地产 | 115 | 9.55 | 12.15 | 0.98 | 3.40 |
| 14 | 801200.SI | 商贸零售 | 104 | 26.10 | 31.57 | 2.60 | 1.51 |
| 15 | 801210.SI | 社会服务 | 73 | 62.34 | 62.04 | 3.57 | 0.55 |
| 16 | 801780.SI | 银行 | 42 | 4.97 | 4.66 | 0.55 | 5.79 |
| 17 | 801790.SI | 非银金融 | 88 | 13.64 | 16.67 | 1.38 | 2.56 |
| 18 | 801230.SI | 综合 | 24 | 57.83 | 30.57 | 2.31 | 0.78 |
| 19 | 801710.SI | 建筑材料 | 74 | 9.34 | 12.55 | 1.48 | 3.83 |
| 20 | 801720.SI | 建筑装饰 | 158 | 8.50 | 7.91 | 0.89 | 2.35 |
| 21 | 801730.SI | 电力设备 | 265 | 40.19 | 29.25 | 4.07 | 0.60 |
| 22 | 801890.SI | 机械设备 | 398 | 24.07 | 27.19 | 2.34 | 1.69 |
| 23 | 801740.SI | 国防军工 | 98 | 55.91 | 50.13 | 3.74 | 0.49 |
| 24 | 801750.SI | 计算机 | 268 | 39.49 | 43.27 | 3.89 | 0.88 |
| 25 | 801760.SI | 传媒 | 140 | 18.93 | 21.97 | 1.88 | 2.49 |
| 26 | 801770.SI | 通信 | 107 | 17.89 | 15.99 | 1.45 | 4.08 |
| 27 | 801950.SI | 煤炭 | 38 | 10.12 | 6.64 | 1.42 | 6.61 |
| 28 | 801960.SI | 石油石化 | 47 | 10.61 | 8.14 | 1.00 | 6.81 |
| 29 | 801970.SI | 环保 | 109 | 16.60 | 18.72 | 1.58 | 1.75 |
| 30 | 801980.SI | 美容护理 | 28 | 43.95 | 42.61 | 5.69 | 0.61 |
这里申万一级的行情数据不在之前的股票数据里,这里提供获取代码:
import akshare as ak
# 申万一级行业信息
sw_index_first_info_df = ak.sw_index_first_info()
for _, sw_series in sw_index_first_info_df.iterrows():
sw_symbol = sw_series["行业代码"].split(".")[0]
_ak_df = ak.index_hist_sw(symbol=sw_symbol, period="day")
_ak_df.to_csv("../data/select_factor_data/sw_{}.csv".format(sw_symbol),index=False)
2. 动量因子选择:阿隆指标(Aroon)
阿隆(Aroon)指标是由图莎尔·钱德(Tushar Chande)1995 年发明的,它通过计算当前价格达到近期最高值和最低值以来所经过的天数,帮助投资者预测证券价格趋势或反转的变化
阿隆指标计算步骤:
- 确定滑动窗口的长度,比如25个工作日);获取这个窗口中日线的最高价与最低价
- 用最高价计算
AroonUp = [(计算期天数-达到最高价后的天数)/计算期天数]*100,即:
Aroonup = [ ( 25 - 到达最高价后的天数 ) / 25] * 100 - 用最低价计算
AroonDown = [(计算期天数-达到最低价后的天数)/计算期天数]*100,即:
Arrondown = [ ( 25 - 达到最低价后的天数 ) / 25 ] * 100
根据公式我们可以推算出:
- 最高价屡创新高时,arronup=1;最低价屡创新低时,arrondown=1;
- 最高价不断走低时,arronup=0;最低价不断走高时,arrondown=0;
- arronup越小,代表离上一次创新高的时间越久;arrondown越小,代表离上一次创新低的时间越久;
- arronup=1且arrondown=1,代表最高价屡创新高的同时,最低价也屡创新低(柱子拉长)
3. 测算方法
1.选择特定的时间区间
我们删除数据不足的“石油石化”,“环保”,“美容护理”,这三个指数,然后划分公共数据区间为两段:
- 统计测算:2015-01-01 至 2020-01-01
- 回测:2020-01-01 至 2023-01-01
#(部分代码)
train_data_dict = {}
test_data_dict = {}
for _sw_key, _sw_df in sw_data_dict.items():
train_data_dict[_sw_key] = _sw_df[_sw_df["日期"].between("2015-01-01", "2020-01-01")]
test_data_dict[_sw_key] = _sw_df[_sw_df["日期"].between("2020-01-01", "2023-01-01")]
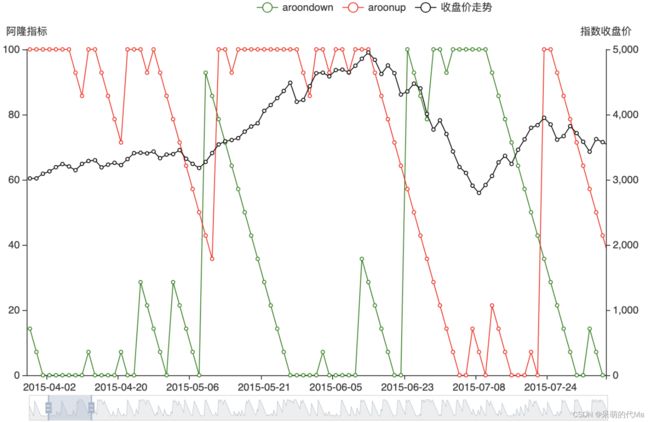
2.计算阿隆指标(Arron)
选择时间区间:2015-01-01 至 2020-01-01,所有指数单独计算,以25天为滑动窗口长度,计算aroonup与aroondown指标
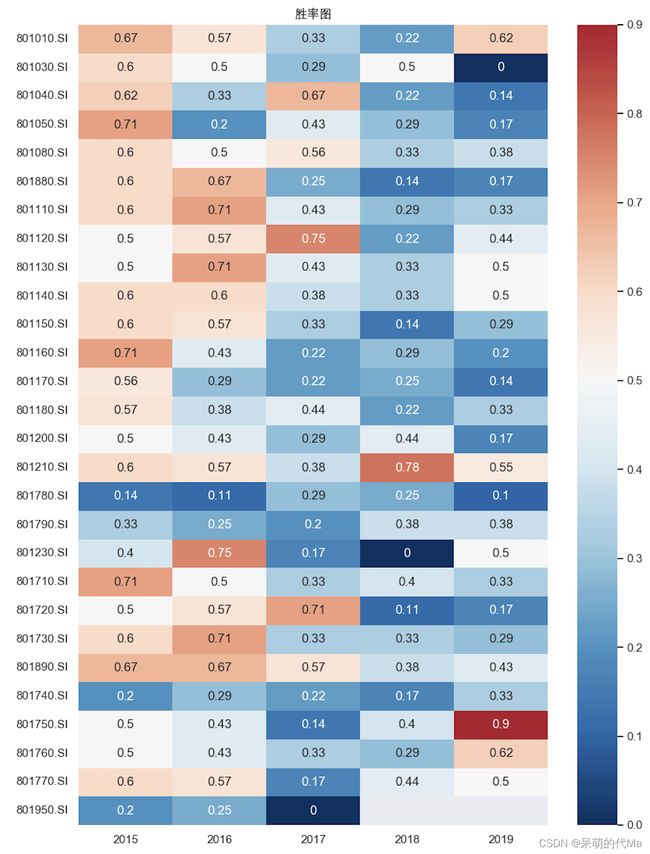
规定交易规则:当arronup>arrondown时,以当天收盘价买入;arronup 统计每一笔完整的交易(从买到卖的完整交易)的年化收益率,并且逐笔统计,以年化收益率>2%记为胜,否则为负 按照上述的测算方法,测算结论如下: 不同指数分年的胜率统计图(0.5为纯白色,越偏红胜率越高,越偏蓝胜率越低):def measure_aroon(dataframe:pd.DataFrame):
dataframe.columns = ["code","date",'close','open','high','low','volume','business_volume']
dataframe.set_index(["date"], inplace=True)
dataframe.index.name = ""
dataframe['aroondown'], dataframe['aroonup'] = talib.AROON(dataframe['high'], dataframe['low'], timeperiod=14)
dataframe = dataframe.dropna()
return dataframe
3. 统计收益率&胜率
# (部分代码)
total_measure_record = {} # 测算结果
for _train_lable,_train_df in train_data_dict.items():
measure_record = {} # 测算结果
if _train_df.shape[0] ==0:
continue
mea_df = measure_aroon(_train_df.copy())
# 开始测算
trade_record_list = []
this_trade = {
"close_record":[],
}
for index,series in tqdm(mea_df.iterrows(),total=mea_df.shape[0]):
if series['aroondown'] < series['aroonup']:
mea_df.loc[index,"label"] = "sell"
if "buy_date" not in this_trade.keys():
continue
this_trade['sell_date'] = index.to_pydatetime()
trade_record_list.append(this_trade)
this_trade = this_trade = {
"close_record":[],
}
else:
mea_df.loc[index,"label"] = "buy"
this_trade['buy_date'] = index.to_pydatetime()
this_trade['close_record'].append(series['close'])
if "buy_date" in this_trade.keys():
this_trade['close_record'].append(series['close'])
trade_record_df = pd.DataFrame(trade_record_list)
for _i,_trade_series in trade_record_df.iterrows():
_trade_record_year_rate = (_trade_series['close_record'][-1] - _trade_series['close_record'][0])/_trade_series['close_record'][0]/(
_trade_series['sell_date'] - _trade_series['buy_date']).days * 365 # 年化收益
if _trade_record_year_rate > 0.02:
trade_record_df.loc[_i,'victory'] = 1
else:
trade_record_df.loc[_i,'victory'] = 0
trade_record_df.loc[_i,'年化收益率'] = _trade_record_year_rate
# trade_record_df 即为每一个行业真实的测算结果
measure_record['胜率'] = round(sum(trade_record_df['victory']) / trade_record_df.shape[0], 4)
measure_record['胜率详情'] = "{}/{}".format(round(sum(trade_record_df['victory']),3), trade_record_df.shape[0])
measure_return = trade_record_df['年化收益率'].describe()
measure_record['收益率均值'] = measure_return['mean']
measure_record['收益率方差'] = measure_return['std']
measure_record['25%'] = measure_return["25%"]
measure_record['75%'] = measure_return["75%"]
measure_record['中位数'] = measure_return['50%']
total_measure_record[_train_lable] = measure_record
4. 测算结论
胜率
胜率详情
“年化收益率均值”
“年化收益率方差”
“年化收益率25%”
“年化收益率75%”
“年化收益率中位数”
801210.SI
0.65
26.0/40
1.101328
13.854513
-3.56732
8.383193
3.277827
801110.SI
0.625
20.0/32
-0.436761
16.563576
-7.324855
7.550573
1.551451
801750.SI
0.6053
23.0/38
-2.006121
22.928017
-6.959875
9.267609
2.499013
801120.SI
0.5897
23.0/39
-0.545812
12.693933
-3.180385
5.897545
1.632406
801890.SI
0.5882
20.0/34
-3.360677
22.453205
-14.620541
8.86559
2.704538
801080.SI
0.5882
20.0/34
-5.754482
25.290329
-8.024543
6.435795
1.120838
801200.SI
0.5758
19.0/33
-5.148041
20.819803
-12.940757
4.352782
1.052707
801140.SI
0.5758
19.0/33
-4.735968
18.721499
-10.971866
6.167402
1.135974
801160.SI
0.5714
20.0/35
-4.535126
17.491513
-7.79196
5.738118
0.732191
801730.SI
0.5588
19.0/34
-2.880497
19.378822
-12.30922
8.174041
0.882168
801010.SI
0.5556
20.0/36
-2.938088
17.975981
-11.395303
8.587668
0.848525
801130.SI
0.5455
18.0/33
-4.977155
21.158295
-8.858312
6.243843
1.500513
801760.SI
0.5312
17.0/32
-10.965525
27.899573
-16.372574
5.734561
0.556964
801770.SI
0.5152
17.0/33
-4.684877
24.414547
-10.702406
10.302837
0.887308
801050.SI
0.5
16.0/32
-4.539061
22.368268
-16.586735
9.285582
0.261408
801040.SI
0.4872
19.0/39
-1.247634
15.297324
-10.782248
6.769093
0.011439
801180.SI
0.4872
19.0/39
-0.804185
16.592557
-3.995552
5.56817
0
801720.SI
0.4865
18.0/37
-3.747824
19.616045
-15.068235
6.508659
0
801710.SI
0.4737
18.0/38
-3.010197
17.654178
-7.417362
5.759873
-0.061242
801030.SI
0.4688
15.0/32
-1.807822
17.684925
-6.325593
8.010072
-0.742137
801880.SI
0.4688
15.0/32
-3.92876
19.513424
-9.694596
6.653341
-1.287274
801170.SI
0.45
18.0/40
-0.845161
13.940707
-5.724337
4.644774
-0.482324
801790.SI
0.4474
17.0/38
-5.057097
20.558703
-15.525831
4.800522
-0.754778
801150.SI
0.4062
13.0/32
-6.399064
18.282151
-14.534501
4.495543
-1.321404
801230.SI
0.4062
13.0/32
-7.866193
27.87652
-13.145653
6.940749
-1.782862
801740.SI
0.3333
11.0/33
-9.563876
20.308132
-17.15555
1.213517
-6.112185
801950.SI
0.2857
4.0/14
-15.703477
37.098001
-25.434644
0.683044
-0.548628
801780.SI
0.2683
11.0/41
-3.816884
10.615774
-6.979213
0.250093
-0.675727