异常检测方法总结

本文收集整理了公开网络上一些常见的异常检测方法（附资料来源和代码），不足之处，还望批评指正。

原文链接：异常检测方法总结

一、基于分布的方法

1. 3sigma

基于正态分布，3sigma准则认为超过3sigma的数据为异常点。

图1: 3sigma

def three_sigma(s):    mu, std = np.mean(s), np.std(s)    lower, upper = mu-3*std, mu+3*std    return lower, upper

2. Z-score

Z-score为标准分数，测量数据点和平均值的距离，若A与平均值相差2个标准差，Z-score为2。当把Z-score=3作为阈值去剔除异常点时，便相当于3sigma。​​​​​​​

def z_score(s):  z_score = (s - np.mean(s)) / np.std(s)  return z_score

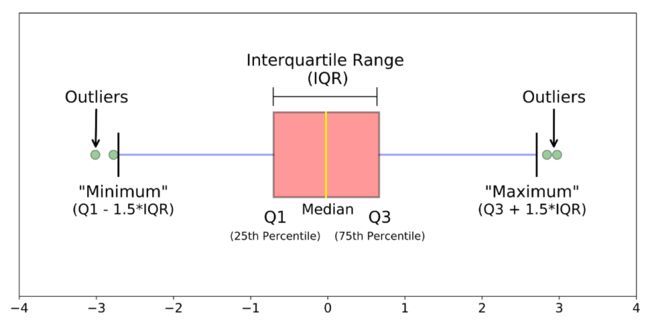
3. boxplot

箱线图时基于四分位距（IQR）找异常点的。

​​​​​​​

def boxplot(s):    q1, q3 = s.quantile(.25), s.quantile(.75)    iqr = q3 - q1    lower, upper = q1 - 1.5*iqr, q3 + 1.5*iqr    return lower, upper

 4. Grubbs假设检验

资料来源：

[1] 时序预测竞赛之异常检测算法综述 - 鱼遇雨欲语与余，知乎：https://zhuanlan.zhihu.com/p/336944097

[2] 剔除异常值栅格计算器_数据分析师所需的统计学：异常检测 - weixin_39974030，CSDN：https://blog.csdn.net/weixin_39974030/article/details/112569610

Grubbs’Test为一种假设检验的方法，常被用来检验服从正态分布的单变量数据集（univariate data set）Y中的单个异常值。若有异常值，则其必为数据集中的最大值或最小值。原假设与备择假设如下：

● H0: 数据集中没有异常值

● H1: 数据集中有一个异常值

使用Grubbs测试需要总体是正态分布的。算法流程：

1. 样本从小到大排序

2. 求样本的mean和dev

3. 计算min/max与mean的差距，更大的那个为可疑值

4. 求可疑值的z-score (standard score)，如果大于Grubbs临界值，那么就是outlie

Grubbs临界值可以查表得到，它由两个值决定：检出水平α（越严格越小），样本数量n，排除outlier，对剩余序列循环做 1-4 步骤 [1]。详细计算样例可以参考。​​​​​​​

from outliers import smirnov_grubbs as grubbsprint(grubbs.test([8, 9, 10, 1, 9], alpha=0.05))print(grubbs.min_test_outliers([8, 9, 10, 1, 9], alpha=0.05))print(grubbs.max_test_outliers([8, 9, 10, 1, 9], alpha=0.05))print(grubbs.max_test_indices([8, 9, 10, 50, 9], alpha=0.05))

局限：

1、只能检测单维度数据

2、无法精确的输出正常区间

3、它的判断机制是“逐一剔除”，所以每个异常值都要单独计算整个步骤，数据量大吃不消。

4、需假定数据服从正态分布或近正态分布

二、基于距离的方法

1. KNN

资料来源：

[3] 异常检测算法之(KNN)-K Nearest Neighbors - 小伍哥聊风控，知乎：https://zhuanlan.zhihu.com/p/501691799

异常检测算法之(KNN)-K Nearest Neighbors

依次计算每个样本点与它最近的K个样本的平均距离，再利用计算的距离与阈值进行比较，如果大于阈值，则认为是异常点。优点是不需要假设数据的分布，缺点是仅可以找出全局异常点，无法找到局部异常点。​​​​​​​

from pyod.models.knn import KNN
# 初始化检测器clfclf = KNN( method='mean', n_neighbors=3, )clf.fit(X_train)# 返回训练数据上的分类标签 (0: 正常值, 1: 异常值)y_train_pred = clf.labels_# 返回训练数据上的异常值 (分值越大越异常)y_train_scores = clf.decision_scores_

三、基于密度的方法

1. Local Outlier Factor (LOF)

资料来源：

[4] 一文读懂异常检测 LOF 算法（Python代码）- 东哥起飞，知乎：https://zhuanlan.zhihu.com/p/448276009

手动计算LOF异常检测算法

LOF是基于密度的经典算法（Breuning et. al. 2000），通过给每个数据点都分配一个依赖于邻域密度的离群因子 LOF，进而判断该数据点是否为离群点。它的好处在于可以量化每个数据点的异常程度（outlierness）。

图3：LOF异常检测

数据点P的局部相对密度（局部异常因子）=点P邻域内点的平均局部可达密度 跟  数据点P的局部可达密度 的比值： 数据点P的局部可达密度=P最近邻的平均可达距离的倒数。距离越大，密度越小。 

点P到点O的第k可达距离=max(点O的k近邻距离，点P到点O的距离)。 

图4：可达距离

点O的k近邻距离=第 k个最近的点跟点O之间的距离。

整体来说，LOF算法流程如下：

● 对于每个数据点，计算它与其他所有点的距离，并按从近到远排序；

● 对于每个数据点，