Leetcode（240）——搜索二维矩阵 II

Leetcode（240）——搜索二维矩阵 II

题目

编写一个高效的算法来搜索 $m\ast n$ 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：

• 每行的元素从左到右升序排列。
• 每列的元素从上到下升序排列。

题解

方法一：直接查找

思路

​​  直接遍历整个矩阵 $\text{matrix}$，判断 $\text{target}$ 是否出现即可。

代码实现

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        for (const auto& row: matrix) {
            for (int element: row) {
                if (element == target) {
                    return true;
                }
            }
        }
        return false;
    }
};

复杂度分析

时间复杂度：$O(N\ast M)$ ，其中 $N$ 和 $M$ 都为矩阵边长
空间复杂度：$O(1)$

方法二：单行或单列的二分查找

思路

​​​​  看到有序，第一反应就是二分查找。最直接的做法，一行一行或一列一列的进行二分查找即可。
​​  此外，结合有序的性质，一些情况可以提前结束。（代码实现没写这些情况）
  ​​  1. ​​比如某一行的第一个元素大于了 target ，当前行和后边的所有行都不用考虑了，直接返回 false。
  ​​  ​​2. 某一行的最后一个元素小于了 target ，当前行就不用考虑了，换下一行。

​​  1. 由于矩阵 $\text{matrix}$ 中每一行和每一列的元素都是升序排列的，所以每一行和每一列都是有序的；
​​  2. 因此我们可以对每一行都使用一次二分查找，判断 $\text{target}$ 是否在该行中，从而判断 $\text{target}$ 是否出现。当然也可以选择对每一列使用一次二分查找。

代码实现

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        for (const auto& row: matrix) {
        	// 下面介绍两个 STL 算法的原理都是二分查找，且都假设数组有序
        	// lower_bound 是 STL 算法库的一个算法，返回迭代器指向范围 [begin, end) 中
        	// 首个不小于（即大于或等于）给定值的元素的迭代器，或若找不到这种元素则返回 end
        	// upper_bound 是 STL 算法库的一个算法，返回迭代器指向范围 [begin, end) 中
        	// 首个大于给定值的元素的迭代器，或若找不到这种元素则返回 end
            auto it = lower_bound(row.begin(), row.end(), target);	
            if (it != row.end() && *it == target){
                return true;
            }
        }
        return false;
    }
};

复杂度分析

时间复杂度：$O(m\log n)$ ，$m$ 表示行个数，$n$ 表示列个数，对每一行使用二分查找的时间复杂度为 $O(\log n)$，最多需要进行 $m$ 次二分查找
空间复杂度：$O(1)$

方法三：矩形整体的二分查找（一种特殊的“二分”查找）

思路

​​  我们都知道，二分查找的思想就是，将目标值和待查找的有序数组的中心值进行比较，然后可以少查找一半的元素。
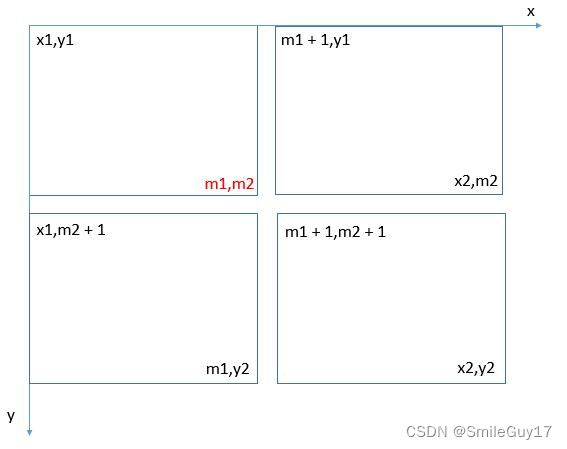
​​  而这道题，待查找的目标不是有序数组，而是一个”特殊的“有序矩阵——每行的元素从左到右升序排列，每列的元素从上到下升序排列（即以某个值为右下角的矩阵的其它值都比该值要小，以该值为左上角的矩阵的其它值都比该值要大）。
​​  如果我们找到矩阵的中心值，然后就可以和目标值比较，看能少查找哪些元素。

如果 target = 10，此时中心值小于目标值，左上角矩形中所有的数都小于目标值，我们可以丢弃左上角的矩形，继续从剩下三个矩形中寻找
如果 target = 5，此时中心值大于目标值，右下角矩形中所有的数都大于目标值，那么我们可以丢弃右下角的矩形，继续从剩下三个矩形中寻找

• 可以用递归的形式去写，递归出口的话，当矩阵中只有一个元素，直接判断当前元素是不是目标值即可。
• 还有就是分割的时候可能越界，比如原矩阵只有一行，左下角和右下角的矩阵其实是不存在的，按照上边的坐标公式计算出来后，我们要判断一下是否越界。

代码实现

class Solution {
	// 2 dimension binary search
private:
	bool binary_search_matrix(vector<vector<int>>& matrix, int target, int m_1, int m_2, int n_1, int n_2) {
		// check border
		if (m_1 > m_2 || n_1 > n_2) {
			return false;
		}
		if (m_2 - m_1 <= 1 && n_2 - n_1 <= 1) {
			return target == matrix[m_1][n_1] || 
				target == matrix[m_2][n_1] || 
				target == matrix[m_1][n_2] ||
				target == matrix[m_2][n_2];
		}

		int m_mid = (m_1 + m_2) >> 1, n_mid = (n_1 + n_2) >> 1;
		// 中心值是否等于目标值
		if (target == matrix[m_mid][n_mid]) {
			return true;
		}
		else if (target < matrix[m_mid][n_mid]) {
			return binary_search_matrix(matrix, target, m_1, m_mid - 1, n_mid + 1, n_2) ||//up-right 
				binary_search_matrix(matrix, target, m_mid + 1, m_2, n_1, n_mid - 1) ||//down-left
				binary_search_matrix(matrix, target, m_1, m_mid, n_1, n_mid); //up-left
		}
		else {//target > matrix[m_mid][n_mid]
			return binary_search_matrix(matrix, target, m_1, m_mid - 1, n_mid + 1, n_2) ||//up-right 
				binary_search_matrix(matrix, target, m_mid + 1, m_2, n_1, n_mid - 1) ||//down-left
				binary_search_matrix(matrix, target, m_mid, m_2, n_mid, n_2); //down-right
		}
	}
public:
	bool searchMatrix(vector<vector<int>>& matrix, int target) {
		return binary_search_matrix(matrix, target, 0, matrix.size() - 1, 0, matrix[0].size() - 1);
	}
};

复杂度分析

时间复杂度：$O(m+n)$ ，$m$ 表示行个数，$n$ 表示列个数
空间复杂度：$O(1)$

方法四：Z 字形查找（二分排序树思想）

思路

​​  数组从左到右和从上到下都是升序的，如果从右上角出发开始遍历呢？
​​  会发现每次都是向左数字会变小，向下数字会变大，有点和二分查找树相似。二分查找树的话，是向左数字变小，向右数字变大。

​​  我们可以从矩阵 $\text{matrix}$ 的右上角 $(0,n-1)$ 进行搜索。在每一步的搜索过程中，如果我们位于位置 $(x,y)$，那么我们希望在以 $\text{matrix}$ 的左下角为左下角、以 $(x,y)$ 为右上角的矩阵中进行搜索，即行的范围为 $[x,m-1]$，列的范围为 $[0,y]$：

• 如果 $\text{matrix}[x,y]=\text{target}$ ，说明搜索完成；
• 如果 $\text{matrix}[x,y]>\text{target}$ ，由于每一列的元素都是升序排列的，那么在当前的搜索矩阵中，所有位于第 $y$ 列的元素都是严格大于 $\text{target}$ 的，因此我们可以将它们全部忽略，即将 $y$ 减少 $1$；
• 如果 $\text{matrix}[x,y]<\text{target}$ ，由于每一行的元素都是升序排列的，那么在当前的搜索矩阵中，所有位于第 $x$ 行的元素都是严格小于 $\text{target}$ 的，因此我们可以将它们全部忽略，即将 $x$ 增加 $1$。

​​  在搜索的过程中，如果我们超出了矩阵的边界，那么说明矩阵中不存在 $\text{target}$。

代码实现

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        int m = matrix.size(), n = matrix[0].size();
        int x = 0, y = n - 1;
        while (x < m && y >= 0) {
            if (matrix[x][y] == target) {
                return true;
            }
            if (matrix[x][y] > target) {
                --y;
            }
            else {
                ++x;
            }
        }
        return false;
    }
};

​​  通过缓存一下 matrix[x][y]，每个循环可以减少一次 operator[](){} 的调用，总体算下来可以快不少。
​​  因为 matrix 是 vector 不是内置数组， vector 的 [] 运算符不是内置要释放，所以就不是简单的地址偏移了。它实际上调用了 std::vector::operator[] ，是函数调用。

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        int Y = matrix[0].size();
        int x = matrix.size() - 1;
        int y = 0;
        while (x > -1 && y < Y) {
            int t = matrix[x][y];
            if (t == target) {
                return true;
            }
            if (t > target) {
                --x;
            } else {
                ++y;
            }
        }
        return false;
    }
};

复杂度分析

时间复杂度：$O(m+n)$ ，$m$ 表示行个数，$n$ 表示列个数，在搜索的过程中，如果我们没有找到 $\text{target}$，那么我们要么将 $y$ 减少 $1$，要么将 $x$ 增加 $1$。由于 $(x,y)$ 的初始值分别为 $(0,n-1)$，因此 $y$ 最多能被减少 $n$ 次，$x$ 最多能被增加 $m$ 次，总搜索次数为 $m+n$。在这之后，$x$ 和 $y$ 就会超出矩阵的边界
空间复杂度：$O(1)$