数据结构与算法C语言版学习笔记（1）-绪论

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

---

一、数据结构的研究内容

举个例子：
研究一个班级成绩表，表里有同学的名字、学号、成绩、排名，要进行增删改查操作——线性表
研究一个大文件夹里面的小文件夹，进行增删改查——树状结构
研究地图导航，要求一个地点到另一个地点的最短路径——网状结构

共性：无法用数学方式来描述这类问题，是非数值计算问题。

二、基本概念与术语

1.数据与数据元素

数据：

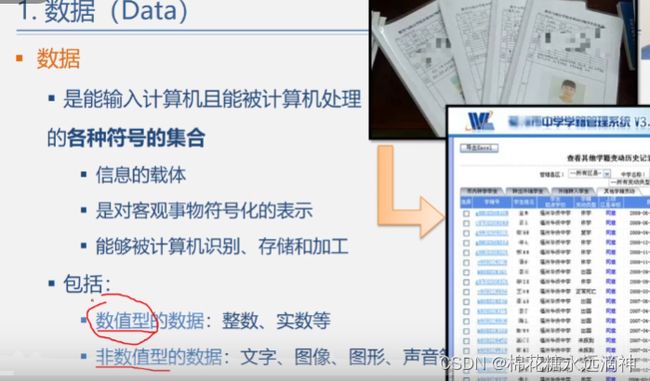
数据元素：

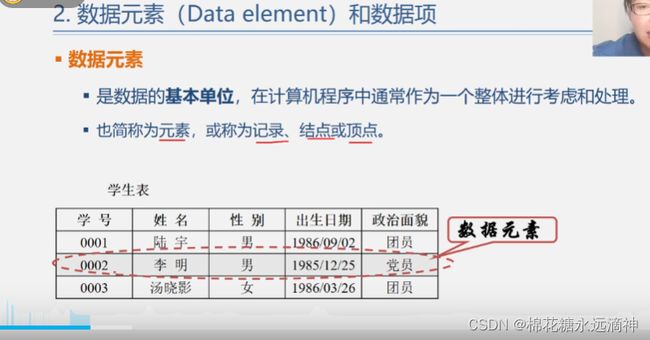
数据项：数据项是构成数据元素的不可分割的最小单位。

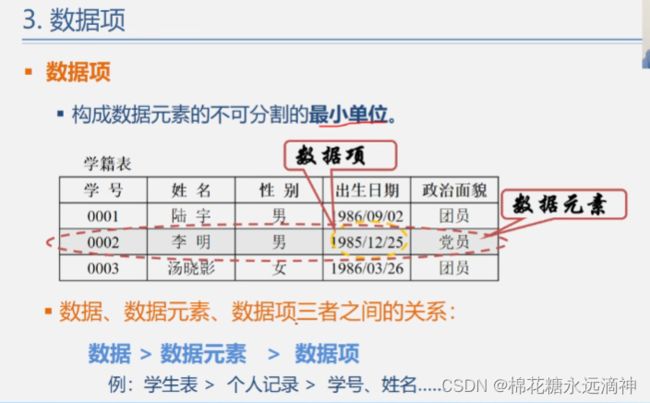
数据对象：性质相同的数据元素的集合。

2.数据结构

这里引出了一个关键性的知识：逻辑结构和存储结构。
我以C语言为例：
我们定义一个const int a[5]，那么这5个元素在逻辑结构上就是线性排列的，而从计算机内部存储结构，他们被依次存入flash内存中，地址是连续的。

逻辑结构的种类

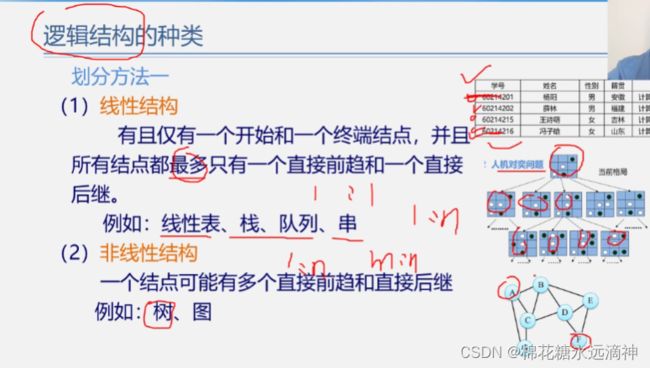
（1）线性结构：线性结构是指数据元素之间存在一对一的关系，数据元素之间只有一个直接前驱和一个直接后继。

①线性表：线性表是具有相同数据类型的 n 个数据元素的有限序列，其中元素之间的关系是一对一的关系。常见的线性表有数组和链表。
②栈：栈是一种特殊的线性表，只能在一端进行插入和删除操作，即后进先出（LIFO）的原则。
③队列：队列也是一种特殊的线性表，只能在一端进行插入操作，在另一端进行删除操作，即先进先出（FIFO）的原则。
④串：串是一种特殊的线性表，它是由零个或多个字符组成的有限序列，其中字符之间的关系是一对一的关系。

（2）非线性结构：非线性结构是指数据元素之间存在一对多或多对多的关系，数据元素之间可以有多个直接前驱和直接后继

①树：树是由 n（n>=0）个结点组成的有限集合，其中一个结点称为根结点，其余结点可以分为多个互不相交的子集，每个子集本身又是一棵树。树的特点是一个结点可以有多个子节点，但每个结点只能有一个父节点。
②图：图是由顶点的有穷非空集合和顶点之间的边的集合组成。图的特点是顶点之间可以有多个边，边可以有方向。

总的来说，线性结构和非线性结构分为这四类：

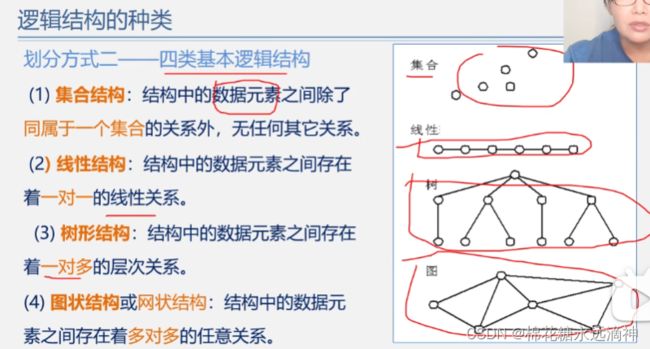
他们本质是这些数据元素之间存在着的不同关系。

存储结构的种类

主要介绍这两种类型：顺序存储结构和链式存储结构。
顺序存储结构和链式存储结构是两种常见的数据结构存储方式。

（1）顺序存储结构：顺序存储结构是将数据元素存储在一块连续的存储空间中。在顺序存储结构中，数据元素的物理存储位置是连续的，可以通过下标或偏移量来直接访问元素。常见的顺序存储结构有数组。

优点：
访问速度快：由于元素在内存中连续存储，可以通过下标直接访问，因此访问速度较快。
存储密度高：不需要额外的存储空间来存储指针或链接信息，存储密度高。
缺点：
大小固定：顺序存储结构的大小是固定的，一旦分配了固定大小的空间，无法动态扩展或缩小。
插入和删除操作慢：在顺序存储结构中，插入和删除元素需要移动其他元素，时间复杂度较高。

(2)链式存储结构：链式存储结构是通过节点之间的指针或链接来实现数据元素的存储。在链式存储结构中，每个节点包含数据元素和指向下一个节点的指针。常见的链式存储结构有链表。

优点：
动态存储：链式存储结构可以根据需要动态分配和释放存储空间，可以灵活地增加或删除元素。
插入和删除操作快：在链式存储结构中，插入和删除元素只需要修改指针的指向，时间复杂度较低。
缺点：
访问速度慢：由于节点之间的链接需要通过指针进行跳转，访问元素的速度较慢。
存储密度低：链式存储结构需要额外的指针来存储节点之间的链接信息，存储密度低。

选择顺序存储结构还是链式存储结构取决于具体的应用场景和需求。顺序存储结构适用于对元素的访问频繁，而插入和删除操作较少的情况。链式存储结构适用于需要动态分配和释放存储空间，插入和删除操作较频繁的情况。

这里我用C语言给一个例子：

存储方式：
数组：数组使用一块连续的内存空间来存储元素，元素之间的内存地址是连续的。数组的大小在创建时就确定，且一旦分配了固定大小的空间，大小就无法动态改变。
链表：链表使用节点来存储元素，每个节点包含数据和指向下一个节点的指针。节点在内存中可以是分散的，通过指针将它们链接起来。链表的大小可以动态增加或缩小。

插入和删除操作：
数组：在数组中插入或删除元素时，涉及到元素的移动。插入元素时，需要将插入位置后面的元素向后移动，删除元素时，需要将删除位置后面的元素向前移动。这些操作可能会导致较大的时间复杂度。
链表：在链表中插入或删除元素时，只需要修改节点的指针指向即可，不需要移动其他节点。这些操作时间复杂度较低。

访问元素的效率：
数组：数组通过下标来访问元素，可以直接通过下标计算出元素在内存中的位置。因此，访问数组元素的效率很高。
链表：链表中的节点之间通过指针链接，访问链表元素需要通过指针跳转，因此，相对于数组，访问链表元素的效率较低。

存储密度：
数组：数组在存储元素时不需要额外的指针或链接信息，存储密度高。
链表：链表中每个节点都需要存储指向下一个节点的指针，因此，链表的存储密度较低。

三、算法

1.什么是算法？算法的描述

算法是一组解决问题的明确步骤和指令。它是一种有序的操作序列，用于解决特定问题或完成特定任务。算法可以用来执行各种计算、数据处理和自动化任务。它可以是数学公式、计算机程序、流程图等形式。算法的目标是通过一系列有限的步骤来解决问题，并且在有限的时间内产生正确的结果。算法可以用来解决各种问题，比如排序、搜索、加密、图像处理等。

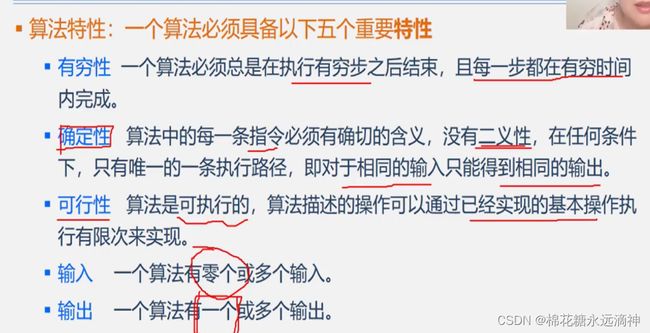
2.一个算法要具备的特性

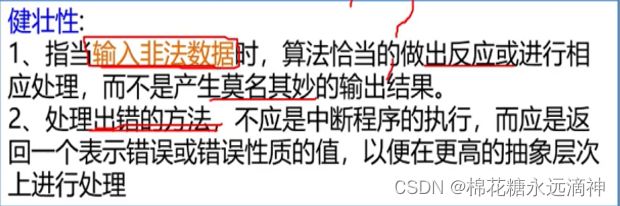
3.算法设计的要求？

高效性和可读性顾名思义，不用再去解释。

四、衡量算法优劣的两个重要特性：时间复杂度和空间复杂度

1.对于时间复杂度，直接上例子：

大循环套小循环，每个循环内语句执行次数之和就是时间复杂度。
但是，这样用多项式来表示的话，形式比较复杂，所以不太好。这时候引入无穷小，外面加一个O，作为同阶无穷小。

也就是说用渐进时间复杂度来度量算法的时间好坏。用其中最多的执行次数的语句的时间作为总体的时间

那么如何具体的计算一个算法的时间复杂度呢？

例①

要点：找到算法中执行次数最多的那条语句。
明显，对于其中一个二重循环，最里面的sum【i】+=x[i][j]，外循环执行一次，内循环执行n次，外循环执行m次，内循环执行mn次，其他语句最多执行m次，所以时间复杂度为O（mn）。

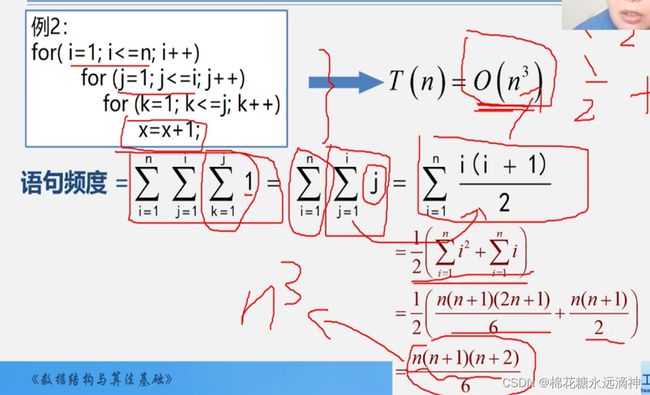
例二

最里面循环的执行语句一般次数最多，这里i循环执行一次，j循环执行n次，k循环执行n*n次，则i循环执行n次，k循环执行n^3次，所以时间复杂度为O（n的3次方）。

例三

采用如图的计算方法，变成一个数学问题来计算：

例四

关于伪代码，要找到执行次数x与n的关系。

2.时间复杂度的其他情况

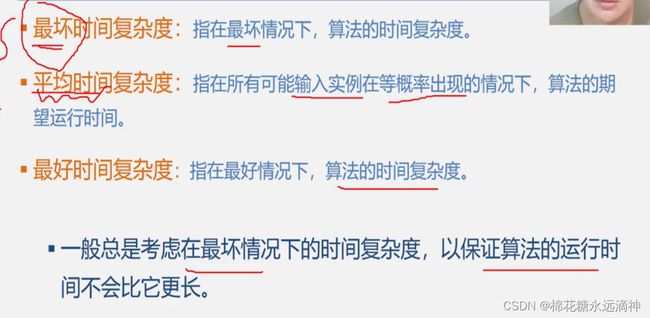
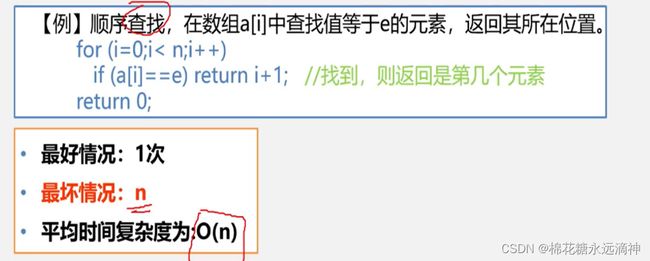
对于一个算法，它的执行次数不一定是固定的，那么就会存在最少和最多的执行次数的可能。比如这个例子，要查找数组中的某个元素，那么这个语句的执行次数有可能最好1次就找到了，但是也有可能一直要执行到n次才能找到。

我们通常只考虑最坏时间复杂度，保证算法的运行时间在一个可控的范围内。
以下是时间复杂度的大小排序：

3.渐进空间复杂度

渐进空间复杂度是衡量算法在处理输入规模增大时所需的额外空间的度量。它表示算法所使用的额外空间的增长趋势。

常见的渐进空间复杂度有以下几种：

O(1)：常数空间复杂度，表示算法所使用的额外空间是一个常数。不随输入规模的增大而变化。

O(n)：线性空间复杂度，表示算法所使用的额外空间随输入规模的增大而线性增长。

O(n^2)：平方空间复杂度，表示算法所使用的额外空间随输入规模的增大而平方增长。

O(log n)：对数空间复杂度，表示算法所使用的额外空间随输入规模的增大而对数增长。

O(n log n)：线性对数空间复杂度，表示算法所使用的额外空间随输入规模的增大而线性对数增长。

需要注意的是，渐进空间复杂度只考虑算法所使用的额外空间，不包括输入数据所占用的空间。在计算渐进空间复杂度时，通常忽略常数因子和低阶项，只关注最高阶项。和时间复杂度类似，渐进空间复杂度也使用大O表示法来表示。