深度学习-softmax回归

二分类激活函数使用Sigmoid,多分类使用Softmax

1- softmax 基本概念

$$\begin{gathered} {\hat{y}}_1,{\hat{y}}_2,{\hat{y}}_3=Softmax(O1,O2,O3) \\ {\hat{y}}_1=\frac{exp(O1)}{{\sum }_{i=1}^{3}exp(O_i)} \end{gathered}$$

实现softmax由三步构成：
1.对每个项求幂
2.对每一行求和（小批量中每个样本是一行），得到每个样本的规范化常数；
3.将每一行除以其规范化常数，确保结果的和为1。
$$Softmax(X{)}_{ij}=\frac{exp(X_{ij})}{{\sum }_{k}exp(X_{ik})}$$
输出变换成一个合法的类别预测分布

def softmax(x):
    x_exp=torch.exp(x)
    partition = x_exp.sum(1, keepdim=True)#keepdim=True表示输出原来的纬度
    return x_exp / partition  # 这里应用了广播机制
#softmax(torch.mm(w,x)+b)

• softmax直白来说就是将原来输出是3,1,-3通过softmax函数一作用，就映射成为(0,1)的值，而这些值的累和为1（满足概率的性质），
  那么我们就可以将它理解成概率，
  在最后选取输出结点的时候，我们就可以选取概率最大（也就是值对应最大的）结点，作为我们的预测目标！

softmax回归适用于分类问题。它使用softmax运算输出类别的概率分布。
softmax回归是一个单层神经网络，输出个数等于分类问题中的类别个数。

1-1 极大似然估计

用一个损失函数来度量预测的效果的话，使用极大似然估计。
softmax函数给出一个向量$\hat{y}$,我们可以将其视为"对给定任意输入x的每个类的条件概率"。如 ${\hat{y}}_1=P(y=猫|x)$ . 假设整个数据集 {X，Y} 具有n个样本，其中索$i$的样本由特征向量$x^i$和独热标签变量$y^{(i)}$组成。 我们可以将估计值与实际值进行比较：
$$P(Y|X)=\prod _{i=1}^{n}P(y^{(i)}|x^{(i)})$$
根据最大似然估计，我们最大化$P(Y|X)$，相当于最小化负对数似然：
$$-logP(Y|X)=\sum _{i=1}^n-logP(y^i|x^i)=\sum _{i=1}^{n}l(y^i,{\hat{y}}^i)$$

其中对于任何标签$y$和模型预测$\hat{y}$,损失函数为
$$l(y,\hat{y})=-\sum _{j=1}^q{y}_{j}log{\hat{y}}_j$$

由于是一个长度为的独热编码向量， 所以除了一个项以外的所有项$j$都消失了。 由于所有${\hat{y}}_i$都是预测的概率，所以它们的对数永远不会大于0.一般来说数据集都会存在标签噪声，或输入特征没有足够的信息来完美地对每一个样本分类。因此不可能预测结果的$P(y|x)=1,损失函数不能进一步优化的。$

2- Fashion-MNIST图像分类数据集

阐述
Fashion-MNIST中一共包括了10个类别，分别为 t-shirt（T恤）、trouser（裤子）、pullover（套衫）、dress（连衣裙）、coat（外套）、sandal（凉鞋）、shirt（衬衫）、sneaker（运动鞋）、bag（包）和ankle boot（短靴）。数据集也就几十M
以下函数可以将数值标签转成相应的文本标签。

torchvision包，它是服务于PyTorch深度学习框架的，主要用来构建计算机视觉模型。torchvision主要由以下几部分构成：

• torchvision.datasets: 一些加载数据的函数及常用的数据集接口；
• torchvision.models: 包含常用的模型结构（含预训练模型），例如AlexNet、VGG、ResNet等；
• torchvision.transform: 常用的图片变换，例如裁剪、旋转等；
• torchvision.utils: 其他的一些有用的方法。
  
  

2-1 下载数据集

import torch
import torchvision
import torchvision.transforms as transforms
import matplotlib.pyplot as plt
import time,sys

mnist_train = torchvision.datasets.FashionMNIST(root='../Datasets/FashionMNIST', train=True, download=True, transform=transforms.ToTensor())
mnist_test = torchvision.datasets.FashionMNIST(root='../Datasets/FashionMNIST', train=False, download=True, transform=transforms.ToTensor())

变量feature对应高和宽均为28像素的图像。由于我们使用了transforms.ToTensor()，所以每个像素的数值为[0.0, 1.0]的32位浮点数。需要注意的是，feature的尺寸是 (C x H x W) 的，而不是 (H x W x C)。第一维是通道数，因为数据集中是灰度图像，所以通道数为1。后面两维分别是图像的高和宽

当你jupyter kernel挂掉了的话，添加

import os
os.environ['KMP_DUPLICATE_LIB_OK']='True'

2-2 可视化

1-画图

from IPython import display
from torch.utils import data as Data

def use_svg_display():
    # 用矢量图显示
    display.set_matplotlib_formats('svg')
def set_figsize(figsize=(3.5, 2.5)):
    use_svg_display()
    # 设置图的尺寸
    plt.rcParams['figure.figsize'] = figsize
#绘图函数
def show_images(imgs, num_rows, num_cols, titles=None, scale=1.5):  #@save
    """绘制图像列表"""
    figsize = (num_cols * scale, num_rows * scale)
    _, axes = plt.subplots(num_rows, num_cols, figsize=figsize)
    axes = axes.flatten()
    for i, (ax, img) in enumerate(zip(axes, imgs)):
        if torch.is_tensor(img):
            # 图片张量
            ax.imshow(img.numpy())
        else:
            # PIL图片
            ax.imshow(img)
        ax.axes.get_xaxis().set_visible(False)
        ax.axes.get_yaxis().set_visible(False)
        if titles:
            ax.set_title(titles[i])
    return axes

>> mnist_train[0][0].shape#torch.Size([1, 28, 28])
def get_finish_minist_label(x):
    """返回Fashion-MNIST数据集的文本标签"""
    text_labels=['t-shirt', 'trouser', 'pullover', 'dress', 'coat',
                   'sandal', 'shirt', 'sneaker', 'bag', 'ankle boot']
    return [text_labels[int(i)] for i in x]
    
X, y = next(iter(data.DataLoader(mnist_train, batch_size=18)))
show_images(X.reshape(18, 28, 28), 2, 9, titles=get_finish_minist_label(y));

2-详情

#样本的shape 
mnist_train[0][0].numpy().shape#(1, 28, 28)
#画图需要将其纬度3维转2维（28,28）
img = mnist_train[7][0].numpy()  # 将张量转换为 NumPy 数组
img = img.squeeze()  # 去掉维度为 1 的维度（灰度图像只有一个通道）
plt.imshow(img)

3- softmax回归简洁代码实现

3.1-导包

import torch
from torch import nn
from torch.nn import init
import numpy as np
import torchvision

3.2-批量读取数据

batch_size = 256
if sys.platform.startswith('win'):
    num_workers = 0  # 0表示不用额外的进程来加速读取数据
else:
    num_workers = 4
train_iter = torch.utils.data.DataLoader(mnist_train, batch_size=batch_size, shuffle=True, num_workers=num_workers)
test_iter = torch.utils.data.DataLoader(mnist_test, batch_size=batch_size, shuffle=False, num_workers=num_workers)

3.3 定义模型初始化

• 得到的每个样本的大小(1,28,28),样本的形状为（batch_size,1,28,28）,softmax输出层是一个全连接层，全连接层需要flatten化，因此需要转换为(batch_size,28*28)才送入全连接层

+ 第一种方式

num_inputs = 784#28*28
num_outputs = 10#labels

class LinearNet(nn.Module):
	def __init_(self,num_inputs,num_outputs):
		super(LinearNet,self).__init__()
		self.linear = nn.Linear(num_inputs,num_outputs)
	def forward(self,x):
		y = self.linear(x.view(x.shape[0],-1))
		return y
model = LinearNet(num_inputs,num_outputs)
>>model 
>LinearNet(
  (linear): Linear(in_features=784, out_features=10, bias=True)
)
model.linear 
#我们将对x的形状转换的这个功能自定义一个FlattenLayer
class FlattenLayer(nn.Module):
	def __init__(self):
		super(FlattenLayer,self).__init__()
	def forward(self,x):
		return x.view(x.shape[0],-1)#torch.Size([1, 784])

+ 第2种方式以Sequential

from collections import OrderedDict
#创建网络
net = nn.Sequential(
        OrderedDict([
            ('flatten',FlattenLayer()),
            ('linear',nn.Linear(num_inputs,num_outputs))
            ]))
#初始化权重参数
init.normal_(net.linear.weight,mean=0,std=0.01)#权重
init.constant_(net.linear.bias,val=0)#偏置

#softmax和交叉熵损失函数
loss = nn.CrossEntropyLoss()

#随机梯度下降优化算法
optimizer = torch.optim.SGD(net.parameters(), lr=0.1)

3.4 训练模型

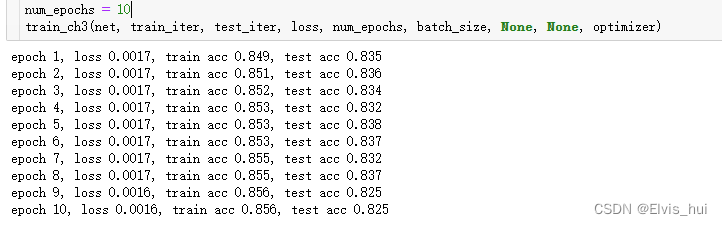
def train_ch3(net, train_iter, test_iter, loss, num_epochs, batch_size, params=None, lr=None, optimizer=None):
    for epoch in range(num_epochs):  # 迭代训练轮数
        # 初始化本轮训练损失、训练准确率、样本数量
        train_l_sum, train_acc_sum, n = 0.0, 0.0, 0
        for X, y in train_iter:  # 迭代每个小批量
            y_hat = net(X)  # 前向传播计算预测值
            
            l = loss(y_hat, y).sum()  # 计算损失

            # 清空梯度
            if optimizer is not None:
                optimizer.zero_grad()
            elif params is not None and params[0].grad is not None:
                for param in params:
                    param.grad.data.zero_()

            l.backward()  # 反向传播计算梯度
            if optimizer is None:
                # 手动更新模型参数
                for param in params:
                    param.data -= lr * param.grad / batch_size  # 注意这里更改param时用的param.data
            else:
                optimizer.step()  # 使用优化器更新模型参数

            train_l_sum += l.item()  # 累计本轮训练损失
            train_acc_sum += (y_hat.argmax(dim=1) == y).sum().item()  # 累计本轮训练正确预测样本数
            n += y.shape[0]  # 累计本轮训练样本数

        test_acc = evaluate_accuracy(test_iter, net)  # 计算测试准确率
        # 输出本轮训练和测试信息
        print('epoch %d, loss %.4f, train acc %.3f, test acc %.3f'
              % (epoch + 1, train_l_sum / n, train_acc_sum / n, test_acc))

4-底层函数实现

#初始化参数
w = torch.tensor(np.random.normal(0,0.01,(num_inputs,num_outputs)),dtype=torch.float)
b = torch.zeros(num_outputs,dtype=torch.float)

#定义softmax回归模型
def softmax(x):
    x_exp=torch.exp(x)
    partition = x_exp.sum(1, keepdim=True)
    return x_exp / partition  

def net(x):
    return softmax(torch.mm(x.view((-1,num_inputs)),w)+b)
#定义损失函数 交叉熵
def cross_entropy(y_hat, y):
    return - torch.log(y_hat.gather(1, y.view(-1, 1)))
______________________________________________________________    
#gather:通过使用gather函数，我们得到了2个样本的标签的预测概率
y_hat = torch.tensor([[0.1, 0.3, 0.6], [0.3, 0.2, 0.5]])
y = torch.LongTensor([0, 2])
y_hat.gather(1, y.view(-1, 1))
>>tensor([[0.1000],
        [0.5000]])
______________________________________________________________   
#准确率
def accuracy(y_hat, y):
    return (y_hat.argmax(dim=1) == y).float().mean().item()

def evaluate_accuracy(data_iter, net):
    acc_sum, n = 0.0, 0
    for X, y in data_iter:
        acc_sum += (net(X).argmax(dim=1) == y).float().sum().item()
        n += y.shape[0]
    return acc_sum / n