包含3的数字-第10届蓝桥杯省赛Python真题精选

[导读]：超平老师的Scratch蓝桥杯真题解读系列在推出之后，受到了广大老师和家长的好评，非常感谢各位的认可和厚爱。作为回馈，超平老师计划推出《Python蓝桥杯真题解析100讲》，这是解读系列的第2讲。

包含3的数字，本题是2019年3月24日举行的第10届蓝桥杯青少组Python编程第2题，题目要求编写程序打印出1~1000之间包含3的数字。

先来看看题目的要求吧。

一.题目说明

编程实现：

打印出 1~1000之间包含3的数字；

如果3是连在一起的（如233）则在数字前加上&；

如果这个数字是质数则在数字后加上*，例:（3,13*,23*,&33,43*…&233*…）。

输入描述：

无

输出描述：

按照题意输出的数字，每行一个数字；

样例输出：

3

13*

23*

&33

……

将程序命名为“lq002”。

评判标准：

• 10 分：完成打印 1~1000 之间包含3的数字；

• 30 分：在 10 分标准的基础上，找出其中的连3，前面加&；

• 50 分：在 30 分标准的基础上，找出其中的质数，后面加*。

二.思路分析

这是一道综合性的题目，考察的知识点包括循环、类型转换、质数的判断等。

看到题目描述，超平老师的第一感觉是题意不够清晰。细心的你也许已经注意到了，这里有两个值得商榷的地方。

1). 题目要求打印出 1~1000之间包含3的数字，正常理解的话，会输出3、13、23、30、31、32等所有包含3的数字，但从输出样例来看，并没有包含30、31、32这些数字；

2). 3是质数，应该在数字后面加上*；

为了避免理解上的分歧，我把题目意思统一一下，从3开始，每隔10个数，进行一次判断，在输出结果时，3后面应该加*。

从3开始，到1000为止，每隔10进行一次判定，这个比较容易，直接使用for...in循环即可，如下：

for i in range(3, 1000, 10)

这里的难点有如下两个：

• 如何判断连3的数字；

• 质数的判断；

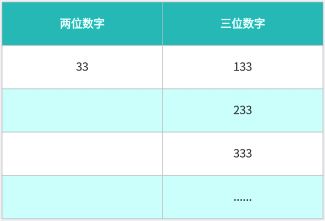
先来分析第1个问题，在1000以内，连3的情况，最多只有3个，具体情况可以如下表所示：

聪明的你肯定已经发现了，3位数字的连3是包含两位的连3，因此只需要判断两位连3即可。

在Python中没有直接判断是否包含子数字的方法，但是字符串可以，可以先将数字转成字符串，然后使用in运算符判断即可，例如：

'33' in str(133)

第1个问题解决了，再来看第二个问题，如何判断质数呢？

质数又称素数，一个大于1的自然数，除了1和它自身外，不能被其他自然数整除的数叫做质数，否则称为合数，注意1既不是质数也不是合数。

下图列出了50以内的质数：

从上面的定义就很容易想到判断方法，对于一个整数n，从2开始到n - 1，逐个判断是否能被整除，如果有，就不是质数，否则就是合数。

为了方便起见，我们可以定义一个函数，用于判断是否为质数，返回布尔值True或False。

思路有了，接下来，我们就进入具体的编程实现环节。

三.编程实现

根据上面的思路分析，我们分两步来编写代码：

• 定义判断质数的函数

• 打印数字

1. 定义判断质数的函数

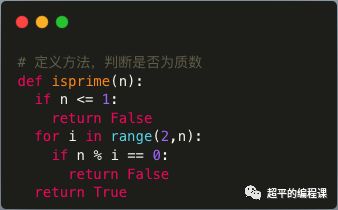
根据上面的思路分析，我们可以快速地编写代码如下：

需要注意的是，为了确保完整性，需要增加一个 <= 1的判断。

从结果来看，这个程序是对的，但是效率不高，比如当数字为97时，按照上面的程序，需要判断95次，实际上，我们最多只需要判断8次就行，你知道为什么吗？

以数字24为例，24的因数有如下8个：

我们可以把它们分成4组：

1 * 242 * 123 * 84 * 6

发现这里面的规律了吗？

以4为分界线，左边有一个因数，那么右边必然也有一个因数，二者的乘积刚好是24，它们是对称的。

再来看看36的情况，它有10个因数，如图：

以6作为分界线，左边有一个因数，右边必然有一个因数与之对应，其乘积刚好是36。

那么，这里的分界线是多少呢？

相信你已经发现了，分界线就是数字的算术平方根的整数部分，对于36而言，其算术平方根刚好是6，对于24而言，其算术平方根为4.89898，取整数部分为4。

所以，在判断整数n是否为素数的时候，我们并不需从2到n - 1都判断一次，因为它包含了很多无效和重复判断，只需要判断2到n的平方根（取整）即可。

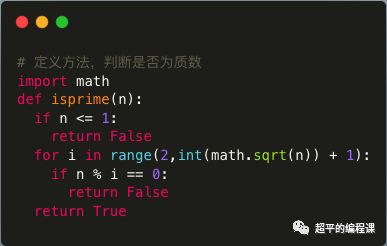
结合数学函数库，可以将上述代码进行优化如下：

这样可以极大地提升判断素数的效率，数字越大，提升的效率越明显。

有两个细节需要注意：

1). sqrt()函数得到的结果是小数，需要使用int函数进行取整，int会直接去掉小数部分，保留整数部分，不是四舍五入；

2). range()函数的特点是虎头蛇尾（有头无尾），所以需要再加上1，确保包含n的算术平方根（比如数字36算术平方根6）；

如果你彻底理解了这两点，还可以使用ceil()函数简化，代码如下：

for i in range(2, math.ceil(n))

效果完全一样，ceil() 函数返回一个大于或等于 x 的的最小整数。

2. 打印数字

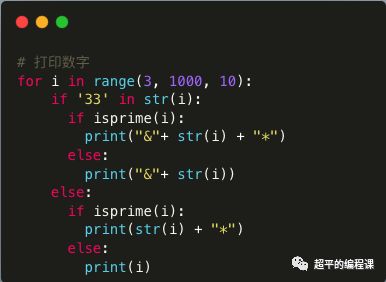
根据前面的思路分析，编写代码如下：

简单说明3点：

1). 由于是从3开始，每隔10个数进行判断，所以数字必然是包含3的，只需要判断是否包含33即可；

2). 输出的时候，需要将数字转成字符串，再进行连接操作；

3). 函数的定义必须要放在前面，因为Python是解释性语言，在执行代码的时候是从上到下边解释边执行的。 

运行程序，输出结果如下：​​​​​​​

3*13*23*&3343*53*6373*83*93103*113*123&133143153163*173*183193*203213223*&233*......

这里只列出了从3到233的数字，为节省篇幅，后面的部分就省略了。

至此，整个程序就全部完成了。

四.总结与思考

本题是中级组编程部分第2题，分数为50分，代码在20行左右，涉及到的知识点包括：

• 循环语句，简单的枚举算法；

• 条件语句的嵌套使用；

• 函数的定义及使用；

• 类型转换；

• 字符串的运算；

题目难度中等，涉及到的知识点还是挺多的，这就要求考生具备扎实的基础，对3大程序结构（顺序、选择、循环）要非常熟悉，并快速找到最简单的方法。

关于质数（素数）的判断，这是一个经典的编程问题，首先要掌握最基础的算法，然后再考虑是否可以进行优化。

说到质数，超平老师给你留一个思考题，除了本文给出的两种方法，你还有其他的思路吗？你可以自己想一想，或者查阅相关资料，说不定会有惊喜的发现哟。

如果你觉得文章对你有帮助，别忘了点赞和转发，予人玫瑰，手有余香

需要源码的，可以移步至“超平的编程课”gzh。