【算法学习】算法图解

本文记录算法图解的学习及相关知识的补充，读完后对各类算法有了大致的了解，后续需要进一步学习和代码练习。

第一章 算法简介

• 二分查找的速度比简单查找快得多；

• 算法运行时间并不以秒为单位，而是从其增速的角度衡量的，使用大O表示法。

• 常见大O运行时间：

  • O(log n )，也叫对数时间，这样的算法包括二分查找。
  • O (n)，也叫线性时间，这样的算法包括简单查找。
  • O (n* log n )，这样的算法包括快速排序——一种速度较快的排序算法。
  • O (n2 )，这样的算法包括选择排序——一种速度较慢的排序算法。
  • O (n!)，这样的算法是一种非常慢的算法。包括旅行商问题的解决方案。

第二章 选择排序

• 需要存储多个元素时，可以使用数组或者链表；

  [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-HQztQXkl-1652236917367)(img/算法图解/e7f5bcf8dad44ea69b55b52a55489c11.png)]

• 数组的元素在内存中都在一起；

• 链表的元素是分开的，其中每个元素都存储了下一个元素的地址；

• 数组的读取速度很快、链表的插入和删除速度很快；

• 在同一个数组中，所有元素的类型都必须相同。

第三章 递归

• 递归指的是调用自己的函数，如计算n的阶乘；
• 每个递归函数都有两个条件：
  • 基线条件：函数什么时候不再调用自己；
  • 递归条件：函数调用自己。
• 栈有两种操作：压入和弹出；
• 所有函数调用都进入调用栈，当return后，被从栈中弹出；
• 调用栈可能很长，这将占用大量内存，此时可以使用循环或尾递归。

第四章 快速排序

分而治之，Divide and Conquer,D&C

• 找出尽可能简单的基线条件；

• 不断将问题分解直到满足基线条件；

• 涉及到数组的递归函数常见的基线条件是数组为空或只含一个元素。

快速排序

• 最简单的排序：不需要排序，即数组中只有0或1个元素；

• 两个元素的数组，比较二者的值；

• 多于两个元素的数组，分而治之；

  • 选取一个元素作为基准值（暂取第一个）
  • 分区：遍历，找出比基准值大的和小的元素，分别构成两个数组；
  • 对子数组递归，直到剩下的数组长度小于等于二
  • 子数组排序后，合并

• 实现快速排序时，应随机地选择用作基准值的元素，快速排序的平均运行时间为O(n logn)

大O表示法中的常量

• 在大O表示法中，固定时间量，也即常数c，是忽略不计的，因为一般来说对时间影响更大的是n和logn的区别；
• 大O表示法中的常量有时事关重大，这就是快速排序比合并排序快的原因所在。

第5章 散列（Hash）表

散列函数

• 将输入映射到数字

  • 必须：一致性：对同样的输入，映射的数字必须相同；

  • 理想但不必须：对于不同的输入，映射到不同的数字；

散列表（hash table）：散列函数+数组

• 一种包含额外逻辑的数据结构，由键和值组成；

• 数组和链表都被直接映射到内存，但散列表使用散列函数来确定元素的存储位置；

• 散列表获取元素的速度和数组一样快；

• Python的字典就是散列表。

散列表的应用

• 查找，eg：电话薄；
• 避免重复，eg：投票；
• 缓存，eg：Facebook，当URL在散列表中时，发送缓存中的数据，否则让服务器处理。如此加快了加载速度，并减轻了服务器负担。

冲突

• 总是将不同的键映射到不同值的散列函数难以实现，当不同的键被分配给了同一个值，即冲突；

• 最简单的解决办法，在该位置创建链表，依次存储，但是性能不佳；

• 理想的情况是，散列函数将键均匀映射到散列表的不同位置故一个好的散列函数很重要。

常量时间O(1)

• 散列表在平均情况下的操作时间为O(1)，不意味着马上，而是不论散列表多大，所需时间都相同。

散列表的性能

• 平均情况下，散列表的查找（获取给定索引处的值）速度与数组一样快，而插入和删除速度与链表一样快，兼具两者的优点。但在最糟情况，即有冲突的情况下，散列表的各种操作的速度都很慢。

散列表的实现 避开最糟情况

• 避免冲突的方式

  • 较低的填装因子：元素数/位置总数，越低越不容易冲突（通常超过0.7，就调整散列表的长度）

  • 良好的散列函数：让数组中的值均匀分布。

第6章 广度优先搜索

• 广度优先搜索：寻找解决问题的最短路径的问题，用于图的查找算法。

图

• 图由节点和边组成。一个节点可能与众多节点直接相连。

两类问题

• 从节点A出发，有前往节点B的路径吗？
• 从节点A出发，前往节点B的哪条路径最短？

队列

• 队列：先进先出，First In First Out，FIFO

• 栈：后进先出，Last In First Out，LIFO

使用散列表实现图

• 找销售商的例子，创建一个字典，以graph[“you”] = [“alice”, “bob”, “claire”]、graph[“alice”] = [“peggy”]的形式添加，即以一人为键，其下级关系的所有人的数组为值，由于散列表是无序的，所以添加内容的顺序也没有影响；
• 由于一个人可能同时是多个人的朋友，为了避免重复检查或无限循环，在检查完一个人后，应将其标记为已检查，且不再检查他。

运行时间

• 广度优先搜索的运行时间为O(V+E)，其中V为顶点数，E为边数。

树

• 一种特殊的图，其中没有往后指的边。
• 如果任务A依赖于任务B，在列表中任务A就必须在任务B后面。这被称为拓扑排序，使用它可根据图创建一个有序列表。

补充：深度优先搜索和广度优先搜索

• 参考：BFS和DFS

• DFS 算法：一直往深处走，直到找到解或者走不下去为止：

  

  使用栈保存未被检测的结点，结点按照深度优先的次序被访问并依次被压入栈中，并以相反的次序出栈进行新的检测。

• BFS算法：

使用队列保存未被检测的结点。结点按照宽度优先的次序被访问和进出队列。

第7章 狄克斯特拉算法

• 广度优先搜索找出的是非加权图的最短路径，狄克斯特拉找出的是加权图的最短路径；

• 狄克斯特拉算法的适用范围：没有负权边的有向无环图（有负权边则使用B-F算法）。

步骤

1. 初始化：所有节点的开销（从起点到该节点的最小权重）为无穷大，节点的父节点未知；
2. 对起点的所有邻节点，找出开销小的节点B，并将B的父节点设为起点；
3. 更新B的所有邻节点的开销，如果某邻居A的开销被更新，就说明沿着经过B的路径是开销最小的，所以将A的父节点更新为B；
4. 当B的所有邻节点均被更新后，将B标记为已分析；
5. 重复２、３、４，继续分析除B以外开销最小的节点，更新其所有邻居的开销和父节点，直到除了终点外的所有节点都被分析；
6. 根据父节点可倒推得开销最短的路径。

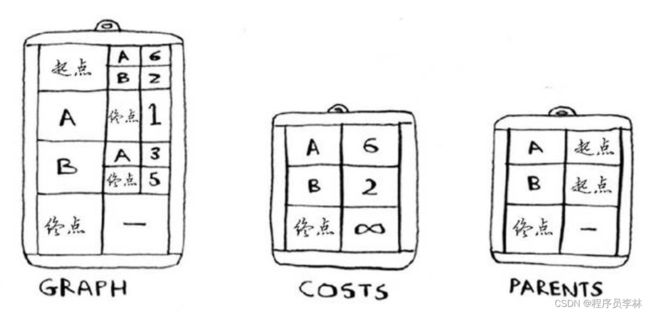
实现

• 需要三个散列表和一个数组；

• graph：记录邻居关系和权重；

• costs：更新开销（从起点到该节点的总权重）；

• parents：更新父节点；

• processed = []：记录已经处理的节点。

• C++源码：

  #include
  #include
  #include
  #include
  using namespace std;
  
  //用邻接矩阵构建有向图
  #define MAX 999//表示无穷
  #define MVNum 20//最大结点数
  typedef int VertexType;//设置结点的数据类型为int型（方便后续修改成char...）
  typedef int ArcType;//设置的权值为int型（方便后续修改成float...）
  
  class Graph//Adjacency Matrix Graph有向图，用邻接矩阵表示
  {
  public:
  	void Create();
  	int LocateVex(VertexType u);//查找Graph中的顶点u，并返回其对应在顶点表中的下标，未找到则返回-1
  	int firstadj(int v);
  	int nextadj(int v, int w);
  	void Dijkstra(VertexType start_point);//使用迪杰斯特拉算法打印单源最短路径
  	void Show();//调试用，打印邻接矩阵
  private:
  	VertexType vexs[MVNum];//顶点表,将顶点保存的信息存入此处
  	ArcType arcs[MVNum][MVNum];//邻接矩阵
  	int vexnum, arcnum;//图当前的顶点数和边数
  	vector<queue<VertexType>>path;//保存各结点最短路径的path[i]
  	ArcType dist[MVNum];//最短路径大小
  	bool solved[MVNum];//是否找到最短路径
  };
  int Graph::LocateVex(VertexType u)
  {//查找Graph中的顶点u，并返回其对应在顶点表中的下标，未找到则返回-1
  	int i;
  	for (i = 0; i < this->vexnum; i++)
  	{
  		if (u == this->vexs[i])
  			return i;
  	}
  	return -1;
  }
  int Graph::firstadj(int v)
  {
  	for (int i = 0; i < this->vexnum; i++)
  	{
  		if (this->arcs[v][i] != MAX)
  			return i;
  	}
  	return -1;
  }
  int Graph::nextadj(int v, int w)
  {
  	for (int i = w + 1; i < this->vexnum; i++)
  	{
  		if (this->arcs[v][i] != MAX)
  			return i;
  	}
  	return -1;
  }
  void Graph::Show()
  {
  	for (int i = 0; i < this->vexnum; i++)
  	{
  		for (int j = 0; j < this->vexnum; j++)
  		{
  			cout << setw(4) << this->arcs[i][j] << " ";
  		}
  		cout << endl;
  	}
  }
  void Graph::Create()
  {
  	cout << "请输入总结点数和总边数:";
  	cin >> this->vexnum >> this->arcnum;//输入总顶点数和总边数
  	cout << "请输入各结点的信息:";
  	for (int i = 0; i < this->vexnum; i++)
  	{
  		cin >> this->vexs[i];
  	}
  	//初始化邻接矩阵
  	for (int i = 0; i < this->vexnum; i++)
  	{
  		for (int j = 0; j < this->vexnum; j++)
  		{
  			this->arcs[i][j] = MAX;
  		}
  	}
  	//构造邻接矩阵
  	for (int i = 0; i < this->arcnum; i++)
  	{
  		int v1, v2, w;
  		cout << "请输入第" << i + 1 << "条边的起点和终点及其对应的权值:";
  		cin >> v1 >> v2 >> w;
  		int m = LocateVex(v1);
  		int n = LocateVex(v2);
  		this->arcs[m][n] = w;
  	}
  	return;
  }
  void Graph::Dijkstra(VertexType start_point)
  {
  	//初始化最短距离数组
  	for (int i = 0; i < this->vexnum; i++)
  	{
  		this->dist[i] = MAX;
  	}
  	dist[this->LocateVex(start_point)] = 0;
  	//初始化保存路径的向量
  	queue<VertexType>temp;
  	temp.push(start_point);
  	for (int i = 0; i < this->vexnum; i++)
  	{
  		//（移到for外）queuetemp;
  		//temp.push(start_point);
  		path.push_back(temp);
  		//（不可行）path[i].push(start_point);//将起点作为最初始的路径加入每个结点对应的队列中
  	}
  	//初始化solved数组
  	for (int i = 0; i < this->vexnum; i++)
  	{
  		solved[i] = false;
  	}
  	for (int i = 0; i < this->vexnum; i++)
  	{
  		if (this->arcs[this->LocateVex(start_point)][i] != MAX)
  		{
  			dist[i] = this->arcs[this->LocateVex(start_point)][i];
  			path[i].push(this->vexs[i]);
  		}
  	}
  	solved[this->LocateVex(start_point)] = true;
  	for (int i = 0; i < this->vexnum; i++)
  	{//返回地找
  		ArcType mind = MAX;
  		int v = i;
  		for (int j = 0; j < this->vexnum; j++)
  		{//一个劲地往前走
  			//（移出for）int v = i;
  			if (!solved[j] && dist[j] < mind)
  			{
  				mind = dist[j];
  				v = j;
  			}
  			solved[v] = true;
  			int w = this->firstadj(v);
  			while (w != -1)
  			{
  				if (dist[v] + this->arcs[v][w] < dist[w])
  				{
  					dist[w] = dist[v] + this->arcs[v][w];
  					path[w] = path[v];
  					path[w].push(vexs[w]);
  				}
  				w = this->nextadj(v, w);
  			}
  		}
  	}
  	cout << "从结点" << start_point << "开始到各点的最短路径和路径长度如下:"<<endl;
  	for (int i = 0; i < this->vexnum; i++)
  	{
  		if (dist[i] == MAX)
  		{
  			cout << "无法到达结点" << this->vexs[i] << endl;
  		}
  		else
  		{
  			cout << "抵达结点" << this->vexs[i] << "的最短路径:";
  			int path_length = path[i].size();
  			for (int j = 0; j < path_length; j++)
  			{
  				cout << path[i].front() << " ";
  				path[i].pop();
  			}
  			cout << "长度为" << dist[i] << endl;
  		}
  	}
  }
  int main()
  {
  	Graph s;
  	s.Create();
  	s.Show();
  	VertexType start_point;
  	cout << "请输入起点:";
  	cin >> start_point;
  	s.Dijkstra(start_point);
  	system("pause");
  	return 0;
  }
  
  

第八章 贪婪算法

• 贪婪算法：简单易行，每步都采取最优的做法（局部最优解），得到的就是全局最优解，不仅简单而且通常运行速度很快；但婪算法不是在任何情况下都行之有效。

NP完全问题（Non-deterministic Polynomial）

• 简单定义是，以难解著称的问题，如旅行商问题和集合覆盖问题，有观点认为不可能编写出可快速解决NP完全问题的算法

• 判断一个问题是不是NP完全问题，不存在判断标准，但可以根据问题的特征判断：

  • 元素较少时算法的运行速度非常快，但随着元素数量的增加，速度会变得非常慢；

  • 涉及“所有组合”的问题；

  • 不能将问题分成小问题，必须考虑各种可能的情况；

  • 涉及序列（如旅行商问题中的城市序列）且难以解决；

  • 涉及集合（如广播台集合）且难以解决；

  • 可转换为集合覆盖问题或旅行商问题，那它肯定是NP完全问题。

• 面临NP完全问题时，最佳的做法是采取近似算法，如贪婪算法。

第九章 动态规划

• 动态规划(dynamic programming)是运筹学的一个分支，是求解决策过程最优化的数学方法，把多阶段过程转化为一系列单阶段问题，利用各阶段之间的关系，逐个求解。

背包问题

假设你是一名小偷，背着一个可装4磅的背包。
你可以盗窃的东西如下三件，为了让偷到的东西价值最高，你该选择那些商品？

• 动态规划先解决子问题，再逐步解决大问题。

在这个过程中，填入单元格时用到了下面的公式：

• 背包问题FAQ
  • 沿着一列往下走时， 最大值不可能降低；
  • 各行的排列顺序无关紧要；
  • 增加一件更小的商品时，单元格的按最小商品的重量划分；
  • 使用动态规划时， 要么考虑拿走整件商品， 要么考虑不拿， 而没法判断该不该拿走商品的一部分，但使用贪婪算法可轻松地处理这种情况；
  • 动态规划无法处理相互依赖的情况；
  • 根据动态规划算法的设计， 最多只需合并两个子背包， 即根本不会涉及两个以上的子背包。
• 动态规划功能强大， 它能够解决子问题并使用这些答案来解决大问题。 但仅当每个子问题都是离散的， 即不依赖于其他子问题时， 动态规划才管用 。

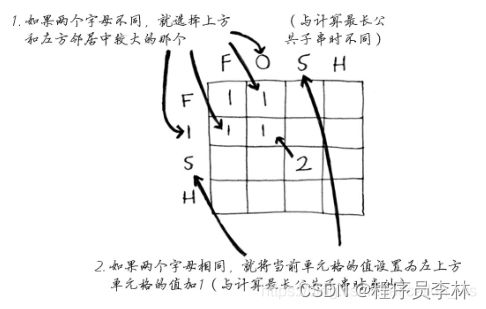
最长公共子串

• 对于背包问题，最终答案总在最后的单元格中；但对于最长公共子串而言，答案是网格中最大的数字——不一定在最后的单元格中。

最长公共子序列

• 比较最长公共子序列：两个单词中都有的序列包含的字母数。

总结

• 需要在给定约束条件下优化某种指标时， 动态规划很有用。
• 问题可分解为离散子问题时， 可使用动态规划来解决。
• 每种动态规划解决方案都涉及网格。
• 单元格中的值通常就是你要优化的值。
• 每个单元格都是一个子问题， 因此你需要考虑如何将问题分解为子问题。

补充案例

• 问题描述：一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法。

第十章 K近邻算法

• KNN可以用来做两项基本工作——分类和回归：

  • 分类就是编组；
  • 回归就是预测结果（如一个数字）；
  • 特征抽取意味着将物品（如水果或用户）转换为一系列可比较的数字，能否挑选合适的特征事关KNN算法的成败。

• 余弦相似度不计算两个矢量的距离，而比较它们的角度。

• OCR（ optical character recognition）：计算机将自动识别出拍摄照片中的文字。 一般而言， OCR算法提取线段、点和曲线等特征；OCR的第一步是查看大量的数字图像并提取特征，这被称为训练（ training）。

• 垃圾邮件过滤器使用一种简单算法——朴素贝叶斯分类器（ Naive Bayes classifier）。

第十一章 接下来如何做

二叉查找树（ binary search tree）

二叉查找树的数据结构类似于下图：

• 对于其中的每个节点，左子节点的值都比它小，右子节点的值都比它大。假设我们要找Maggle，首先检查根节点David，Maggle在David的后面，即比David大，因此往右边找，接下来遇到节点Manning，Maggle在Manning的前面，即比Manning小，因此往左边找，此时找到了Maggle。
• 二叉查找树的优缺点：
  • 优点：插入和删除操作的速度很快；
  • 缺点：有序数组比二叉查找树查找速度更快；不能随机访问；二叉树不平衡会导致性能不佳。

反向索引

• 一个散列表，将单词映射到包含它的页面，这种数据结构被称为反向索引，常用于创建搜索引擎。

傅立叶变换

• 傅立叶变换的绝佳比喻是：给它一杯冰沙，它能告诉你其中包含哪些成分。傅立叶变换非常适合于处理信号，可用它来压缩音乐，还可被用来地震预测和DNA分析。使用傅立叶变换还可创建音乐识别软件。

并行算法

• 并行算法需要让多个内核并行执行，算法速度提升迅速；
• 速度的提升并非线性的，原因有两个：并行性管理开销和负载均衡。

MapReduce

• MapReduce是一种流行的分布式算法（需要数百个内核，让算法在多台计算机上运行，非常适合用于在短时间内完成海量工作），可通过流行的开源工具Apache Hadoop来使用它。MapReduce基于两个简单的理念：映射（map）函数和归并（reduce）函数：
  • 映射函数接受一个数组，对其中的每个元素执行同样的处理，将一个数组转换为另一个数组；
  • 归并函数是将很多项归并为一项。

布隆过滤器和HyperLogLog

• 布隆过滤器是一种概率型数据结构，它提供的答案有可能不对，但很可能是正确的。为判断网页以前是否已搜集，可不使用散列表，而使用布隆过滤器，可能出现错报的情况；
• HyperLogLog是一种类似于布隆过滤器的算法，它近似地计算集合中的不同的元素数，不能给出完全准确的答案，而占用的内存空间却少很多。

SHA算法

• SHA算法称为安全散列算法函数，给定一个字符串，SHA返回其散列值；
• SHA还能让我们在不知道原始字符串的情况下对其进行比较。SHA被广泛用于计算密码的散列值，这种散列算法是单向的，无法推断出原始字符串。

局部敏感的散列算法

• SHA算法是局部不敏感的，希望散列函数是局部敏感的，可使用Simhash。如果对字符串做细微的修改，Simhash生成的散列值也只存在细微的差别。需要检查两项内容的相似度时，Simhash很有用。

Diffie-Hellman密钥交换

• Diffie-Hellman用于对信息的加密，它使用两个密钥：公钥和私钥，公钥是公开的，可将其发布到网上。有人要向你发送消息时，他使用公钥对其进行加密，加密后的消息只有使用私钥才能解答，只要你知道私钥，就能解密消息。

线性规划

• 线性规划用于在给定约束条件下最大限度地改善指定的指标。