KMP算法
目录
一、什么是BF算法
1、概念
2、画图解析
3、代码展示
二、什么是KMP算法
1、概念:
2、画图解析:
3、next数组
(1)肉眼求next数组方式
(2)如何求next数组?
(3)next数组的代码展示
三、KMP算法的实现(Java实现)
代码展示
都看到这了,点个赞再走呗,谢谢谢谢谢!!!
一、什么是BF算法
介绍KMP算法前,我们要先了解BF算法。
1、概念
BF算法,即暴力(Brute Force)算法,是普通的模式匹配算法,BF算法的思想就是将目标串S的第一个字符与模式串T的第一个字符进行匹配,若相等,则继续比较S的第二个字符和 T的第二个字符;若不相等,则比较S的第二个字符和T的第一个字符,依次比较下去,直到得出最后的匹配结果。BF算法是一种蛮力算法。——来自百度百科
而BF算法就是一种字符串模式匹配的算法,给出一个主串和一个子串,判断主串中有没有子串,有就返回子串在主串中的第一个下标。
这种字符串匹配的匹配模式的算法很容易想到,但是时间复杂度很高,假设主串的长度为n,子串的长度为m,最坏情况下的时间复杂度:O(n*m),最好情况下的时间复杂度:O(n+m)。
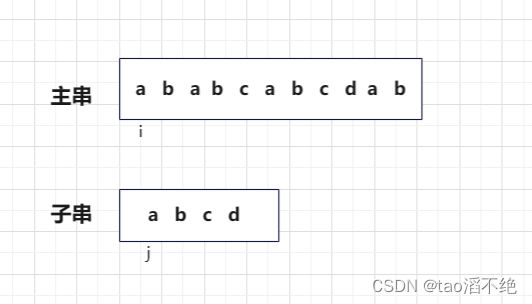
2、画图解析
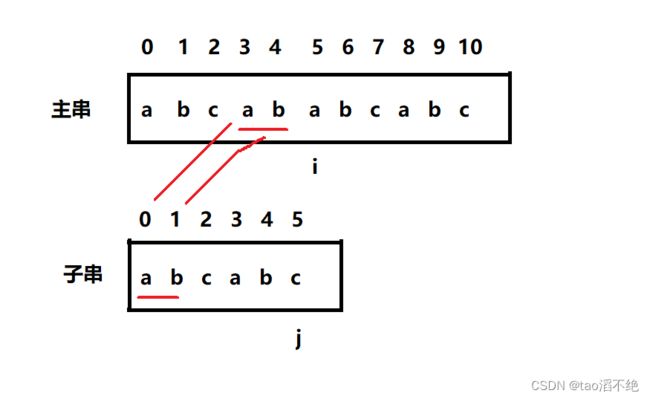
定义i和j,同时遍历i和j,如果i和j下标的元素相同,就同时++,如图,i和j第一次停止遍历位置
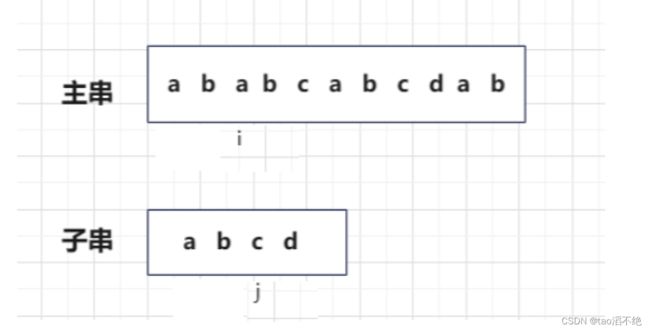
这时,i位置的下标回退到i-j+1位置,但是j下标要到0位置,再次同时遍历,
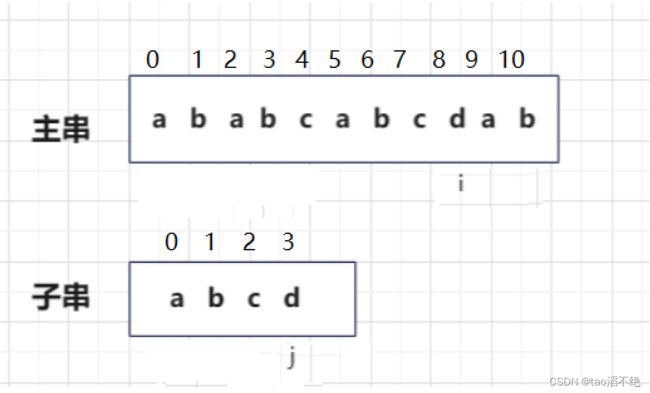
依次类推,直到j能遍历完,就能找到子串在主串第一次出现的位置,i-j就是子串在主串中的首下标,如图:
3、代码展示
public int bf(String str, String sub) { int lenStr = str.length();//主串长度 int lenSub = sub.length();//子串长度 if(str == null || sub == null) { return -1; } if(lenStr == 0 || lenSub == 0) { return -1; } int i = 0;//遍历子串的 int j = 0;//遍历主串的 while (i < lenStr && j < lenSub) { if(str.charAt(i) == sub.charAt(j)) { i++; j++; } else{ i = i - j + 1; j = 0; } } //j遍历完 if(j >= lenSub) { return i - j; } //i没遍历完,j也没遍历完 return -1; }代码解析:
定义i和j下标进行遍历,如果i<主串长度&&j<子串长度,就判断这两下标的元素是否相等,相等就同时++,不相等 i 就要回退到i-j-1下标位置,j就要回退到0位置,重新开始判断,依次类推,直到这个循环结束,判断j是否>=子串长度,如果大于等于就是遍历完j字符串了,我们返回i-j下标位置,没有遍历完就是主串没有这个子串,我们返回一个-1。
二、什么是KMP算法
1、概念:
KMP算法是三位学者在 Brute-Force算法(暴力求解算法)的基础上同时提出的模式匹配的改进算法。Brute- Force算法在模式串中有多个字符和主串中的若干个连续字符比较都相等,但最后一个字符比较不相等时,主串的比较位置需要回退。KMP算法在上述情况下,主串位置不需要回退,从而可以大大提高效率——来自百度百科。
而KMP算法就是一种字符串模式匹配的算法,给出一个主串和一个子串,判断主串中有没有子串,有就返回子串在主串中的第一个下标。
KMP算法和BF算法的区别:KMP算法的i位置下标不会回退,而j位置下标不一定回退到0,而是回退到特殊位置,这个特殊位置我们会用next数组来记录
2、画图解析:
只看概念是不是觉得比较抽象,我们来画图解析一下
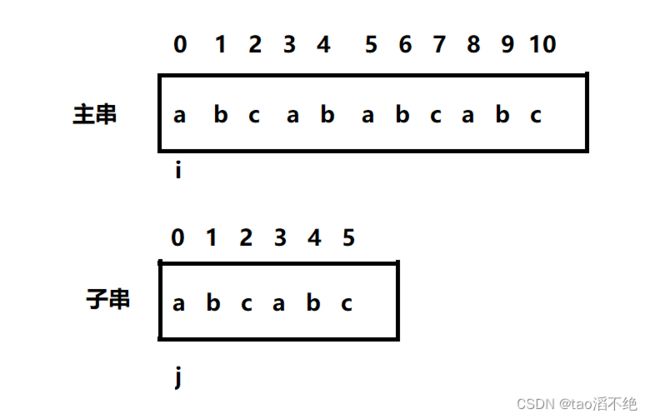
如图:
我们先直接跳过前面的遍历,找到一个比较特殊的j下标,如图:
这种情况,我们知道KMP算法的i下标是不回退的,j下标回退的特定位置,这时,j下标是回退到2位置,如图:
这时我们看,j下标的前面和i下标的前两个元素是不是一样的?那么我们就不用像BF算法那样,把j下标回退到0位置,多遍历这两变。那我们再想想,这种情况是怎么回事呢?
(看这里时对照着图会好理解很多)这是因为i和j能同时走到某个位置,那么前面肯定是有相同的元素的,但是前提还要子串的j下标位置前面有两个相同的字符串,那么i遍历的同时,主串也肯定会遍历到两个相同的字符串,在这基础上如果遍历到某个主串和子串的元素不相同时,那么这时i下标前面的后一个相同的字符串,可以和j下标前一个相同的字符串相匹配,这时,i下标位置是不回退的,j下标就回退到前一个相同的字符串下标+1,而不用回退到0位置了,这也是为啥KMP算法的i下标是不回退的,但是j要回退到某个特定位置,而这个特定位置下标就是第一个相同的字符串末位置+1。
由上面我们可以引出,子串的每一个下标都是有特定的回退位置的,这时我们就要求出这些特定位置,我们把子串回退的特定位置放在next[]数组下标中。
3、next数组
(1)肉眼求next数组方式
求子串的next数组:在子串中找的0下标位置到j-1下标位置,判断是否有两个相同的0下标位置到j-1下标位置的字符串,如果有,子串的j下标位置在next数组中放的就是相同的字符串元素个数,没有的话这个下标j在next数组就放0。
我们先用肉眼来求两个字符串的next数组练练手:
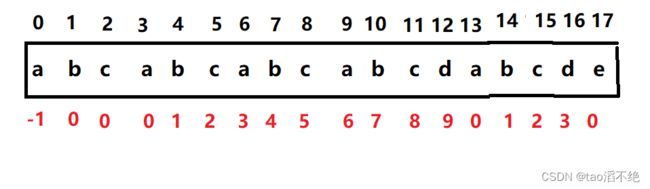
子串:sub = "a,b,a,b,c,,a,b,c,d,,a,b,c,d,e",求next数组
next[0] = -1, next[1] = 0,除了next数组的0下标和1小标比较特殊外,其他都按照上面KMP算法的画图解析步骤来求得,红色字即为下标
所以next[] = {-1,0,0,1,2,0,1,2,0,0,1,2,00}。
子串:sub = "a,b,c,a,b,c,a,b,c,a,b,c,d,a,b,c,d,e",求next数组
所以next[] = {-1,0,0,0,1,2,3,4,5,6,7,8,9,0,1,2,3,0}。
(2)如何求next数组?
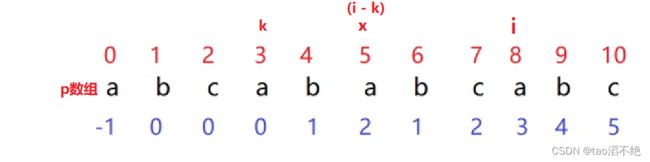
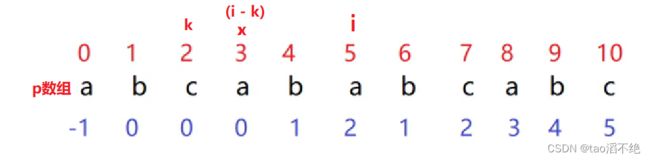
我们求出一个子串中的next数组,如图
假设next[j] = k
那么我们就能写出如下的公式,下面进行公式推导
我们再判断i和k下标位置元素是否相同
i和k下标位置元素相同情况:
推导:
我们是用 i 遍历数组的,这个推导也就是判断 i+1 位置在next数组中的值。
所以,这时:next[i + 1] = k + 1。
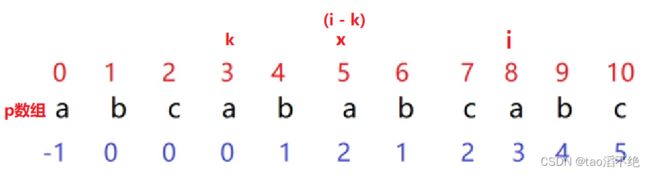
i和k下标位置元素不相同情况:
我们想想next[i+1] = ?
这时,k就要回退到next[k]位置,判断回退完后的值和i下标的值是否相同
如图:
k下标的值和i下标的值相同,那么这种情况就又回到了上面p[i] = p[k]时的情况,处理方法和上面一样:next[i+1] = k+1
那如果k回退到-1位置呢,处理方法也是next[i+1] = k+1,也是i+1下标的next数组为0
(3)next数组的代码展示
注意:我们在代码展示,遍历i的过程中,是不知道当前i下标在next数组中的位置的,但是我们知道前一个下标在next数组中的位置,所以在代码中,我们判断的是next[i-1]和k下标位置的值是否相同,求i下标在next数组中的值。
public static void getNext(String sub, int[] next) { next[0] = -1; next[1] = 0; int i = 2;//提前走了一步 int k = 0;//前一项的k //i下标从2开始 for(;i <= sub.length(); i++) { //p[i-1] = p[k] if (k == -1 || sub.charAt(i - 1) == next[k]) { next[i] = k + 1; k++; } else { //回退 k = next[k]; } } }
三、KMP算法的实现(Java实现)
KMP算法的实现思路和BF思想差不多,只不过子串的回退位置不一样,遍历主串的下标不回退
代码展示
public static int kmp(String str, String sub, int pos) { if(str == null || sub == null) { return -1; } //pos:从pos开始遍历 int lenStr = str.length(); int lenSub = sub.length(); if (lenStr == 0 || lenSub == 0) { return -1; } if(pos < 0 || pos >= lenStr) { return -1; } int i = pos;//遍历str的下标 int j = 0;//遍历sub的下标 int[] next = new int[lenSub]; getNext(sub, next); while(i < lenStr && j < lenSub) { if(j == -1 || str.charAt(i) == sub.charAt((j))) { i++; j++; } else { //i不回退,j回退到next[j]位置 j = next[j]; } } if(j >= lenSub) { return i - j; } return -1; }
和next数组结合的代码呈现情况:
public static void getNext(String sub, int[] next) {
next[0] = -1;
next[1] = 0;
int i = 2;//提前走了一步
int k = 0;//前一项的k
//i下标从2开始
for(;i <= sub.length(); i++) {
//p[i-1] = p[k]
if (k == -1 || sub.charAt(i - 1) == next[k]) {
next[i] = k + 1;
k++;
} else {
//回退
k = next[k];
}
}
}
public static int kmp(String str, String sub, int pos) {
if(str == null || sub == null) {
return -1;
}
//pos:从pos开始遍历
int lenStr = str.length();
int lenSub = sub.length();
if (lenStr == 0 || lenSub == 0) {
return -1;
}
if(pos < 0 || pos >= lenStr) {
return -1;
}
int i = pos;//遍历str的下标
int j = 0;//遍历sub的下标
int[] next = new int[lenSub];
getNext(sub, next);
while(i < lenStr && j < lenSub) {
if(j == -1 || str.charAt(i) == sub.charAt((j))) {
i++;
j++;
} else {
//i不回退,j回退到next[j]位置
j = next[j];
}
}
if(j >= lenSub) {
return i - j;
}
return -1;
}