小伙子，过来咱两聊聊排序（图示+动画） | 十大排序（JS）

排序有比较多的方式，根据不同的方式在不同的场景下有不同的表现，本文一一梳理那些算法。

单纯出于学习目的，网上看了一些实现（文末参考），用图尽量简单的呈现其实现方式。
虽然是用 JS 实现，但是 java, python 都是 js 语言早期抄袭的对象，实现基本大差不差，思路理解即可。另外如行文有误 欢迎 指出~~

---

❗❗ 注意 评价算法优劣术语

• 稳定：如果a原本在b前面，而a=b，排序之后a仍然在b的前面；
• 不稳定：如果a原本在b的前面，而a=b，排序之后a可能会出现在b的后面；
• 内排序：所有排序操作都在内存中完成；
• 外排序：由于数据太大，因此把数据放在磁盘中，而排序通过磁盘和内存的数据传输才能进行；
• 时间复杂度: 一个算法执行所耗费的时间。
• 空间复杂度: 运行完一个程序所需内存的大小。

鄙人不善言辞，来看代码吧。

---

不知道咋的， 算法的 动画网站⇲ 我死活打不开，为了方便理解所以中间有的动画就去拿的别人的图。

另外 【推荐】算法可视化学习

算法讲解

十大算法优劣总览（来源 【github】JS-Sorting-Algorithm⇲）

其实我推荐大家到上面的链接去学习，不同算法实现版本 有 js / java / py / php / go

比较常用就是 快排 和 插入 ，v8 的数组排序接口 Array.sort (快排会提到) 就是用的两者相结合
另外， 归并 的思想也比较值得学习。堆 排序 对递归的利用也是用的很好。

---

归并排序

归并排序（Merge sort）是建立在归并操作上的一种有效的排序算法。该算法是分治法（Divide and Conquer）的一个非常典型的应用。

实现描述

1. 将长度为n的数组不断均分（1分为二，二分为四，…），最后分成二或一项
2. 将最后的两项/一项排序
3. 将排序的项不断合并为一个有序的数组

图示

这里的图画的更美观一点(虽然我也画的不错)

• JavaScript 数据结构与算法之美 - 归并排序、快速排序、希尔排序、堆排序

(注意他这里单数项分的时候有些不一致，他向上取的二分数 Math.ceil(n/2))

动画

图源⇲

另外，上面提到的 算法可视化学习 也可以找到相应的动画，学算法的不二选择。

代码

function mergeSort(items) {
 if (items.length == 1) {
     return items;
 }
 //将数组对半平分为左右两个数组
 var middle = Math.floor(items.length / 2),
     left = items.slice(0, middle),
     right = items.slice(middle);

 function merge(left, right) {
   var result = [];
   // 通过这个循环来排序
   while (left.length > 0 && right.length > 0) {
       if (left[0] <= right[0]) {
           /*shift()方法用于把数组的第一个元素从其中删除，并返回第一个元素的值。*/
           result.push(left.shift());
       } else {
           result.push(right.shift());
       }
   }
   //合并两个数组
   const res =  result.concat(left).concat(right);
   return res;
 }

 // 递归调用
 return merge(mergeSort(left), mergeSort(right));
}

---

快速排序

比较重要的一种排序算法。见名知意，快速排序就是快。

快速排序使用分治法（Divide and conquer）策略来把一个串行（list）分为两个子串行（sub-lists）。
快速排序又是一种分而治之思想在排序算法上的典型应用。本质上来看，快速排序应该算是在冒泡排序基础上的递归分治法。

实现描述

1. 从数列中挑出一个元素，称为 “基准”（pivot）/哨兵;
2. 重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；
3. 递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序；

递归的最底部情形，是数列的大小是零或一，也就是永远都已经被排序好了。虽然一直递归下去，但是这个算法总会退出，因为在每次的迭代（iteration）中，它至少会把一个元素摆到它最后的位置去。

图示

动画

图源⇲

代码

初级版本，浪费了多余的内存空间

function quickSort (arr) {
　　if (arr.length <= 1) { return arr; }
　　var pivotIndex = Math.floor(arr.length / 2);
　　var pivot = arr.splice(pivotIndex, 1)[0];
　　var left = [];
　　var right = [];
　　for (var i = 0; i < arr.length; i++){
　　　　if (arr[i] < pivot) {
　　　　　　left.push(arr[i]);
　　　　} else {
　　　　　　right.push(arr[i]);
　　　　}
　　}
　　return quickSort(left).concat([pivot], quickSort(right));
};

当然还有分成三段 哨兵元素为一段的，这里不做展示，多产生了一些数组，浪费了内存空间.

原地快排

function quickSort(arr) {
  let n = arr.length;
  function sort(arr, start, end) {
    if(end <= start) return;
    let i = start,
        j = end,
        key = arr[start]; // 设置第一个元素为key
    while(true) {
        // 从左向右找到大于key的元素位置(大于key循环停止, i就是该元素位置)
        while(arr[++i] < key) {
            // 到达末尾退出循环
            if(i === end) break;
        }
        // 从右向左找到小于key的元素位置
        while(arr[--j] > key) {
            // 到达头部退出循环
            if(j === start) break;
        }
        // 如果 i和j相交, 直接退出循环
        if(i>=j) break;
        // 交换左右两边元素
        let temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }
    // 交换key和最后一个小于key值的元素(就是arr[j])
    let temp = arr[start];
    arr[start] = arr[j];
    arr[j] = temp;
    sort(arr, start, j);
    sort(arr, j+1, end);
  }
  sort(arr, 0, n);
  return arr;
}

for 循环 + 稍微封装一下。读者体验更好

function inPlace(arr) {
    // 交换元素
    function swap(arr, a, b) {
      var temp = arr[a];
      arr[a] = arr[b];
      arr[b] = temp;
    }
    // 确定哨兵
    function partition(arr, left, right) {
      var pivot = arr[left];
      var storeIndex = left;
      for (var i = left + 1; i <= right; i++) {
        if (arr[i] < pivot) {
          swap(arr, ++storeIndex, i);
        }
      }
      swap(arr, left, storeIndex);
      return storeIndex;
    }
    // 排序递归
    function sort(arr, left, right) {
      if (left < right) {
        var storeIndex = partition(arr, left, right);
        sort(arr, left, storeIndex - 1);
        sort(arr, storeIndex + 1, right);
      }
    }
    sort(arr, 0, arr.length - 1);
    return arr;
}

另外：

• JS-Sorting-Algorithm 快排⇲
• V8快排源码⇲ （下一节有贴部分代码）

v8 Array.sort 快排

前面说过 array.sort 也是也是 快排+插入 实现，贴部分代码

// 部分删减

//https://github.com/v8/v8/blob/fc5765ce7901767ba9298241454f736c17b4f9b3/src/js/array.js#L708
function InnerArraySort(array, length, comparefn) {
	// In-place QuickSort algorithm.
  // For short (length <= 10) arrays, insertion sort is used for efficiency.
	//https://github.com/v8/v8/blob/fc5765ce7901767ba9298241454f736c17b4f9b3/src/js/array.js#L758
	function QuickSort(a, from, to) {
    var third_index = 0;
    while (true) {
      // Insertion sort is faster for short arrays.
      if (to - from <= 10) {
        InsertionSort(a, from, to);
        return;
      }
      if (to - from > 1000) {
        third_index = GetThirdIndex(a, from, to);
      } else {
        third_index = from + ((to - from) >> 1);
      }
      // Find a pivot as the median of first, last and middle element.
      var v0 = a[from];
      var v1 = a[to - 1];
      var v2 = a[third_index];
      var c01 = comparefn(v0, v1);
      if (c01 > 0) {
        // v1 < v0, so swap them.
        var tmp = v0;
        v0 = v1;
        v1 = tmp;
      } // v0 <= v1.
      var c02 = comparefn(v0, v2);
      if (c02 >= 0) {
        // v2 <= v0 <= v1.
        var tmp = v0;
        v0 = v2;
        v2 = v1;
        v1 = tmp;
      } else {
        // v0 <= v1 && v0 < v2
        var c12 = comparefn(v1, v2);
        if (c12 > 0) {
          // v0 <= v2 < v1
          var tmp = v1;
          v1 = v2;
          v2 = tmp;
        }
      }
      // v0 <= v1 <= v2
      a[from] = v0;
      a[to - 1] = v2;
      var pivot = v1;
      var low_end = from + 1;   // Upper bound of elements lower than pivot.
      var high_start = to - 1;  // Lower bound of elements greater than pivot.
      a[third_index] = a[low_end];
      a[low_end] = pivot;

      // From low_end to i are elements equal to pivot.
      // From i to high_start are elements that haven't been compared yet.
      partition: for (var i = low_end + 1; i < high_start; i++) {
        var element = a[i];
        var order = comparefn(element, pivot);
        if (order < 0) {
          a[i] = a[low_end];
          a[low_end] = element;
          low_end++;
        } else if (order > 0) {
          do {
            high_start--;
            if (high_start == i) break partition;
            var top_elem = a[high_start];
            order = comparefn(top_elem, pivot);
          } while (order > 0);
          a[i] = a[high_start];
          a[high_start] = element;
          if (order < 0) {
            element = a[i];
            a[i] = a[low_end];
            a[low_end] = element;
            low_end++;
          }
        }
      }
      if (to - high_start < low_end - from) {
        QuickSort(a, high_start, to);
        to = low_end;
      } else {
        QuickSort(a, from, low_end);
        from = high_start;
      }
    }
}

// https://github.com/v8/v8/blob/fc5765ce7901767ba9298241454f736c17b4f9b3/src/js/array.js#L995
function ArraySort(comparefn) {
  CHECK_OBJECT_COERCIBLE(this, "Array.prototype.sort");

  var array = TO_OBJECT(this);
  var length = TO_LENGTH(array.length);
	// 主要是这一行
  return InnerArraySort(array, length, comparefn);
}

//https://github.com/v8/v8/blob/fc5765ce7901767ba9298241454f736c17b4f9b3/src/js/array.js#L1322
utils.InstallFunctions(GlobalArray.prototype, DONT_ENUM, [
	//"sort", getFunction("sort", ArraySort),
]);

这里快排源码分析可参见： 讶羽大佬的文章 JavaScript专题之解读 v8 排序源码⇲

---

冒泡排序

我大学c语言第一个排序就接触的这个，比较简单。

这个排序就像吐泡泡一样， 交换位置的后一个元素不断变大，最后变到最大处于数组最后面（泡泡到水面，boom , 就爆炸！！！哈哈哈~~~），

实现描述

1. 遍历整个数组，将遍历项相邻元素（0 与 1， 1 与 2, … ）两两比对，
2. 如果前面大就交换位置，第一轮后会将最大元素放在最后面
3. 继续遍历 前 n-1 个数， 再去最大放在最后面
4. 一直到遍历完成。

图示

动画

图源⇲

代码

• 加入 flag ，减少遍历（不用就是原版冒泡）

function bubbleSort(arr) {
  let len = arr.length;
  if (len <= 1) {
    return arr;
  }
  for (let i = 1; i < len; i++) {
    let flag = false; // 开关，当某次内层循环，没有数据交换时，已排好顺序，直接跳出循环。
    for (let j = 0; j < len - i; j++) {
      if (arr[j] > arr[j + 1]) {
        let temp = arr[j];
        arr[j] = arr[j + 1];
        arr[j + 1] = temp;
        flag = true;
      }
    }
    if (!flag) {
      console.log('break: ', i, arr[i]);
      break;
    }
  }
  return arr;
}

---

选择排序

选择排序的稳定性不错，数据规模越小越好，不占用额外内存空间。

其实现思路和冒泡有点像，冒泡是找最大，这是找最小。

实现描述

1. 从 0 开始找出全数组最小与数组第 0个元素交换，
2. 从 1 开始找出剩余最小的 与 第 1 个元素交换
3. 找到 arr.length 整个数组有序

图示

动画

图源⇲

代码

function selectionSort(arr) {
  const len = arr.length;
  let min, index;
  if (len <= 1) {
    return arr;
  }
  for (let i =1; i < len; i++) {
    let j = i-1;
    min = arr[j]; // 最小的数值
    index = j; // 最小值对应的下标
    for (; j < len-1 ; j++) {
      if (min > arr[j+1]) {
        min = arr[j+1];
        index = j+1;
      }
    }
    //最小值a[index]与放未排序的首位a[i-1]互换位置
    if (index != i-1) {
      const temp = arr[i-1];
      arr[i-1] = arr[index];
      arr[index] = temp;
    }
  }
  return arr;
}

---

插入排序

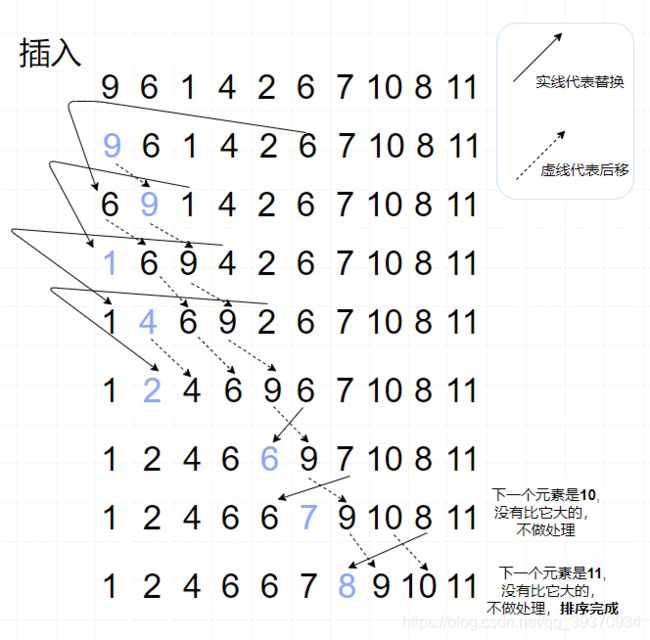
这个也简单，就是将相应的元素插入到相应的位置中。

插入排序（Insertion-Sort）的算法描述是一种简单直观的排序算法。它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。

因为采用原地排序，插入是通过反复交换数组元素位置实现。

实现描述

1. 取出第一个元素，假定已经排序完成，
2. 取出第二个元素 i2，与前面(此时仅有1个)所有元素相比，遇到比 i2 大，就将该元素后移一位（索引+1），
3. 然后将移动元素的原位置替换为 i2
4. 取出第三个元素，重复 步骤1, 2，3

图示

动画

图源⇲

代码

function insertSort(arr) {
  const len = arr.length;
  if (len <= 1) {
    return arr;
  }
  for (let i = 1; i < len; i++) {
    let temp = arr[i];
    let j = i - 1;
    for (; j >= 0; j--) {
      if (arr[j] > temp) {
        arr[j + 1] = arr[j]; // 比temp 大的已排序数据后移一位
      } else {
        break;
      }
    }
    arr[j + 1] = temp; // 空出来的位置，把temp放进去
  }
  return arr;
}
// 精简一下
function insertSort1(arr, start = 0, end){
  end = end || arr.length;
  for(let i = start; i < end; i++) {
    let e = arr[i];
    let j;
    //比较下一个元素与上一个元素大小，如果next < prev 则 next = prev
    for(j = i; j > start && arr[j - 1] > e; j --){
        arr[j] = arr[j-1];
    } 
    arr[j] = e;
  }
  return arr;
}

可以看见，对于每次找位置都是伴随多次移动的，十分不理想，有优化的空间，也就有了下面的希尔排序

---

希尔排序

以前听说过很多排序，希尔倒是第一次听说。

希尔排序，也称递减增量排序算法，是插入排序的一种更高效的改进版本。但希尔排序是非稳定排序算法。

希尔排序 是基于插入排序的以下两点性质而提出改进方法的

• 插入排序在对几乎已经排好序的数据操作时，效率高，即可以达到线性排序的效率；
• 但插入排序一般来说是低效的，因为插入排序每次只能将数据移动一位；

实现描述

1. 将数组以固定的间隔 gap（一般 取 len/2 ）分成很多子组(两个元素组成)，
2. 将两个元素比较（开始是 i , i+gap ）,如果后面大（arr[i+gap] > arr[i]）,则位置互换一直到 i==len。
3. 将间隔以某种速度（一般 1/2）减小，继续进行 1, 2。
4. 数组经过上面步骤会 “ 渐渐有序 “， 最后会 gap == 1,此时进行插入排序。

文字读起来生涩难懂。当你看了图示，动画，代码之后再来看一遍描述就理解了！

图示

动画

图源⇲

代码

function shellSort(arr){
    let gap = arr.length >> 1; // 取中位数相当于 Math.floor(arr.length/2)
    while(d >= 1){
        for(let i = d; i < arr.length; i++){
            let rt = arr[i];
            for(let j = i - d; j >= 0; j -= d){
                if(rt < arr[j]){
                    arr[j + d] = arr[j];
                    arr[j] = rt;
                }else break;
            }
        }
        d >>= 1;// 取中位数
    }
    return arr;
}

js-Sorting-Algorithm 的实现方式（间隔 gap 取的不一样 ）

function shellSort(arr) {
    var len = arr.length,
        temp,
        gap = 1;
    while(gap < len/3) {          //动态定义间隔序列
        gap =gap*3+1;
    }
    for (gap; gap > 0; gap = Math.floor(gap/3)) {
        for (var i = gap; i < len; i++) {
            temp = arr[i];
            for (var j = i-gap; j >= 0 && arr[j] > temp; j-=gap) {
                arr[j+gap] = arr[j];
            }
            arr[j+gap] = temp;
        }
    }
    return arr;
}

相对于 插入排序，希尔排序 在最后的 插入排序 前就让数组 “大致排序” ，那么最后的 插入排序 移动元素的操作将大幅减少，这就是优化的地方。

---

堆排序

堆排序 是相对比较难的排序。因为有前置知识 堆。

关于 堆，补充一些知识。

推荐： javascript-algorithms | 堆(数据结构)

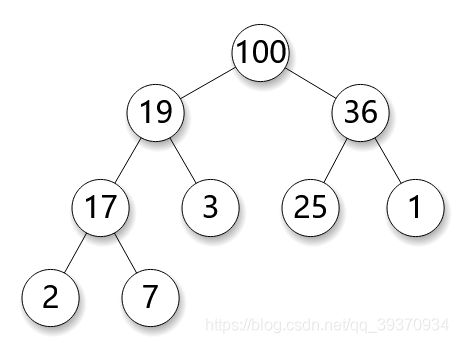
堆是一个特殊的基于树的数据结构（完全二叉树）， 大概这个样子
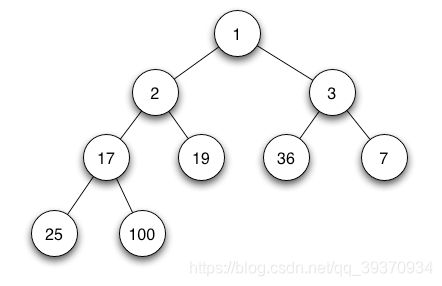图源⇲

堆分为大顶堆(如下)，小顶堆（上图）。

• 大顶堆： 每个结点的值都大于或等于其左右孩子结点的值
• 小顶堆： 每个结点的值都小于或等于其左右孩子结点的值
  
  图源⇲

利用数组如何表示出来呢，上图大顶堆用数组表示

（箭头表示其子元素 ）
图源⇲

堆排序就是不断将大于父节点的最大子节点进行上浮操作，不断减小堆尺寸，不断递归。

实现思路

1. 建堆。将数组进行大项堆建堆操作

1.1. 从最后的子节点的父节点 p 开始，找最大的子节点max与p交换，对发生交换的子节点max再找其子节点最大节点与该子节点max交换，…。
1.2. 再找 p 的前一个节点p1作为开始，进行步骤 1.1
1.3. 一直找到堆顶。

2. 上浮。将堆顶元素与堆尾元素互换。将堆尺寸减一
3. 将新堆（其实就是数组）重复 1, 2.
4. 排序完成。

重点就是 建堆，请看图

图示

如图中所说，后面还会进行n-1次建堆操作，每次建堆的数可以打印查看（后面代码 for 循环 中的console.log）。

动画

图源⇲

代码

function heapSort(arr) {
  buildHeap(arr);
  // 将堆顶元素取出当做最后一个元素，然后从剩余元素再建堆，取堆顶。。
  for(let i=arr.length-1; i>0; i--) {
      // 将每个子节点与根节点的值交换。
      [arr[i], arr[0]] = [arr[0], arr[i]];
      // 每次交换之后都要重新构建堆结构，记得传入i限制范围，防止已经交换的值仍然被重新构建。
  	  // 打印每次交换后的值，建堆的值
      console.log(i, arr);
      heapify(arr, i, 0);
  }
  //console.timeEnd('HeapSort');
  return arr;
  function buildHeap(arr) {
      // 可以观察到中间下标对应最右边叶子节点的父节点。
      let mid = Math.floor(arr.length / 2);
      for(let i=mid; i>=0; i--) {
          // 将整个数组构建成堆结构以便初始化。
          heapify(arr, arr.length, i);
      }
      return arr;
  }
  // 从i节点开始下标在heapSize内进行堆结构构（大顶堆：父节点大于子节点）建的函数。
  function heapify(arr, heapSize, i) {
      // 左子节点下标。
      let left = 2 * i + 1,
          // 右子节点下标。
          right = 2 * i + 2,
          // 假设当前父节点满足要求（比子节点都大）。
          largest = i;
      // 如果左子节点在heapSize内，并且值大于其父节点，那么left赋给largest。
      if(left < heapSize && arr[left] > arr[largest]) {
          largest = left;
      }
      // 如果右子节点在heapSize内，并且值大于其父节点，那么right赋给largest。
      if(right < heapSize && arr[right] > arr[largest]) {
          largest = right;
      }
      if(largest !== i) {
          // 如果largest被修改了，那么交换两者的值使得构造成一个合格的堆结构。
          [arr[largest], arr[i]] = [arr[i], arr[largest]];
          // 递归调用自身，将节点i所有的子节点都构建成堆结构。为后面建堆能减少交换操作。
          heapify(arr, heapSize, largest);
      }
      return arr;
  }
}

---

计数排序

计数排序的核心在于将输入的数据值转化为键存储在额外开辟的数组空间中,要求数据范围确定。

这是一种非比较的排序算法，后面介绍的 桶排序，基数排序 也是如此

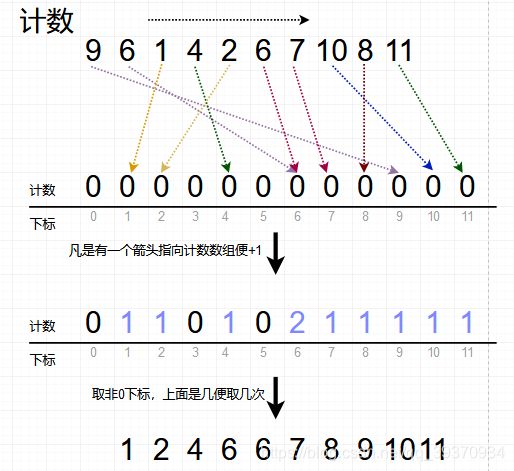
实现描述

1. 找出数组最大项 max,
2. 建一个 长度为· max+1 的数组 countArr（额外空间），每项均为0.
3. 遍历原数组，遇到 项 与 countArr 下标 相等时，将countArr相应项 + 1.
   将 countArr 的非0下标依次拼接起来（项多大就拼接几次）

图示

动画

代码

function countingSort(array) {
  let len = array.length,
    result = [],
    countArr = [],
    min = (max = array[0]);
  for (let i = 0; i < len; i++) {
    // 获取最小，最大 值
    min = min <= array[i] ? min : array[i];
    max = max >= array[i] ? max : array[i];
    countArr[array[i]] = countArr[array[i]] ? countArr[array[i]] + 1 : 1;
  }
  // 从最小值 -> 最大值,将计数逐项相加
  for (let j = min; j < max; j++) {
    countArr[j + 1] = (countArr[j + 1] || 0) + (countArr[j] || 0);
  }
  // countArr 中,下标为 array 数值，数据为 array 数值出现次数；反向填充数据进入 result 数据
  for (let k = len - 1; k >= 0; k--) {
    // result[位置] = array 数据
    result[countArr[array[k]] - 1] = array[k];
    // 减少 countArr 数组中保存的计数
    countArr[array[k]]--;
  }
  return result;
};

精简版

function countingSort(arr) {
   let newArr = new Array(arr.length).fill(0);
   for (const value of arr) {
       if(value > arr.length - 1) newArr[value] = 0;
       newArr[value]++;
   }
   arr = [];
   // 给arr重新赋值
   for(let i =0; i<newArr.length; i++) {
       // 循环数字次数
       for(let k = newArr[i]; k>0; k--) {
         arr.push(i);
       }
   }
   newArr = null;
   return arr;
}

---

桶排序

桶排序 是计数排序的升级版。它利用了函数的映射关系，高效与否的关键就在于这个映射函数的确定

桶排序思路假定数据均匀分布，将数据分到有限数量的桶里，每个桶再分别排序（有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排

• 最好，数据都被分到相应桶里（所以外在空间充足的情况下，尽可能的增加桶数量）。
• 最差，数据都被分到了一个桶里。

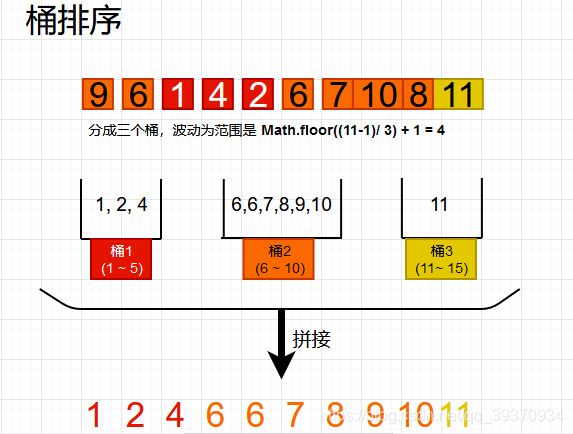
实现描述

1. 确定桶。找出数组中最大项 max 与最小项 min ，假定n个桶，每个桶(下标为 i )只接受相应的数据范围
2. 数据入桶。将所有数据按照大小放入相应的桶。
3. 排序&拼接。 每个桶进行排序（插入排序或者其他排序方式），将桶里数据最后依次拼接起来。

图示

动画

(动画里是固定取五个桶)
图源⇲

代码

function BucketSort(arr, size = 5){
 bucketSort(arr, bucketSize)

 const bucketSort = (array, bucketSize) => {
   if (array.length === 0) {
     return array;
   }

   let i = 0;
   let minValue = array[0];
   let maxValue = array[0];
   for (i = 1; i < array.length; i++) {
     if (array[i] < minValue) {
       minValue = array[i]; //输入数据的最小值
     } else if (array[i] > maxValue) {
       maxValue = array[i]; //输入数据的最大值
     }
   }

   //桶的初始化
   const DEFAULT_BUCKET_SIZE = 5; //设置桶的默认数量为 5
   bucketSize = bucketSize || DEFAULT_BUCKET_SIZE;
   const bucketCount = Math.floor((maxValue - minValue) / bucketSize) + 1;
   const buckets = new Array(bucketCount);
   for (i = 0; i < buckets.length; i++) {
     buckets[i] = [];
   }

   //利用映射函数将数据分配到各个桶中
   for (i = 0; i < array.length; i++) {
     buckets[Math.floor((array[i] - minValue) / bucketSize)].push(array[i]);
   }

   array.length = 0;
   for (i = 0; i < buckets.length; i++) {
     quickSort(buckets[i]); //对每个桶进行排序，这里使用了快速排序
     for (var j = 0; j < buckets[i].length; j++) {
       array.push(buckets[i][j]);
     }
   }
   return array;
 };

---

基数排序

基数排序对大位数排序比较有优势。

基数排序 和 计数排序 & 桶排序 都是非比较整数型排序算法。这三种排序算法都利用了桶的概念，但对桶的使用方法上有明显差异：

• 基数排序：根据键值的每位数字来分配桶；
• 计数排序：每个桶只存储单一键值；
• 桶排序：每个桶存储一定范围的数值；

其实应用场景比较少（前面提过排序一般用快排和插入），当然特殊场景也有应用。

另外：
MSD：由高位为基底，先按 k1 排序分组，同一组中记录,
关键码 k1 相等，再对各组按 k2 排序分成子组, 之后，对后面的关键码继续这样的排序分组，
直到按最次位关键码 kd 对各子组排序后，再将各组连接起来，便得到一个有序序列。
MSD 方式适用于位数多的序列。
LSD：由低位为基底，先从 kd 开始排序，再对 kd - 1 进行排序，
依次重复，直到对 k1 排序后便得到一个有序序列。LSD 方式适用于位数少的序列。

实现描述

1. 开辟内存。建立一个10项数组，
2. 实现个位数有序。遍历数组，将每项 放入该项个位数对应的下标位置 ,相同则在相同个位数的位置插入（可能遍历过程中个位数不一定对应着正确的下标）
3. 实现十位数有序。遍历新的数组（个位数有序），将每项 放入该项十位数对应的下标位置 ,相同则在相同十位数的位置插入（可能遍历过程中十位数不一定对应着正确的下标）。
4. 一直到最大位数最高位完成排序操作。

图示

动画

(掘金gif如何保存我忘记了（虽然我前面刚刚取过，哎~~~），本来打算取这张图 （https://juejin.cn/post/6844903863288332302#heading-34）)

想看的更详细一点的话 去 [这里⇲ ] (https://www.cs.usfca.edu/~galles/visualization/RadixSort.html)

代码

function radixSort(arr) {
  // 获取最大值
  let maxNum = Math.max.apply(Math, arr);
  let t = 1,
    bucketAry = new Array(10), // 0~9的数组,用来计算数字出现次数
    temp = new Array(arr.length); // 交换数组, 用来临时存储排序的数
  const t0 = performance.now();
  // 这一步是计算最大数有多少位,这个位数就是要循环的次数
  while ((maxNum /= 10) >= 1) {
    t++;
  }
  let rate = 1,
      K= null;
  for (let i = 1; i <= t; i++) {
      // 计数数组归零
      bucketAry.fill(0);
      // 清点（个位、十位等等）数字出现次数
      arr.forEach((item) => {
          // 求数字最后一位的值
          k = Math.floor(item / rate) % 10;
          bucketAry[k]++;
      });
      // 通过数字次数得到该数字应该在数组中的位置
      bucketAry.reduce((total, item, index) => {
          bucketAry[index] = total + item;
          return total + item
      });
      // 通过计算的顺序将arr中数存入temp数组中
      for (let j = arr.length - 1; j >= 0; j--) {
          k = Math.floor(arr[j] / rate) % 10;
          temp[bucketAry[k] - 1] = arr[j];
          bucketAry[k]--;
      }
      // 将temp相同位置的值负值给arr, 不能直接 arr = temp
      arr = arr.map((item, index)=>temp[index]);
      rate *= 10;
  }
  const t1 = performance.now();
  temp = null;
  bucketAry = null;
  return arr;
}

---

闲话

其实排序是算法的入门，言外之意是相对简单的。

排序思想不难，但是对入门算法还是比较重要的。我对那些想出这些算法的人还是比较【敬佩】的。

另外，其实我们平常只要随时 能手写快排，插入排序就可以了。这么多排序方式不用很快就忘了（我反正是三天必忘）

–

参考

除去文章中给的链接，还有一些 参考

站在别人肩膀上能看的更远，谢谢以下文章作者~~~

• 掘金 | 十大经典排序算法总结（JavaScript描述）

• 掘金 | 五分钟看懂一个高难度的排序：堆排序

• 掘金 | 这或许是东半球讲十大排序算法最好的一篇文章

• 掘金 | JavaScript专题之解读 v8 排序源码

• 力扣 | 复习基础排序算法（Java）

• 力扣 | 【动画模拟】一个破堆排我搞了四个动画

• github | JS-Sorting-Algorithm

• 博客园 | JS-排序算法之计数和基数排序

• CSDN | 排序（上）——为什么插入排序比冒泡排序更受欢迎？

• CSDN | 三种简单排序（冒泡、插入、选择）的比较和图解