代码随想录笔记--单调栈篇

目录

1--单调栈

2--每日温度

3--下一个更大元素I

3--下一个更大元素II

4--接雨水

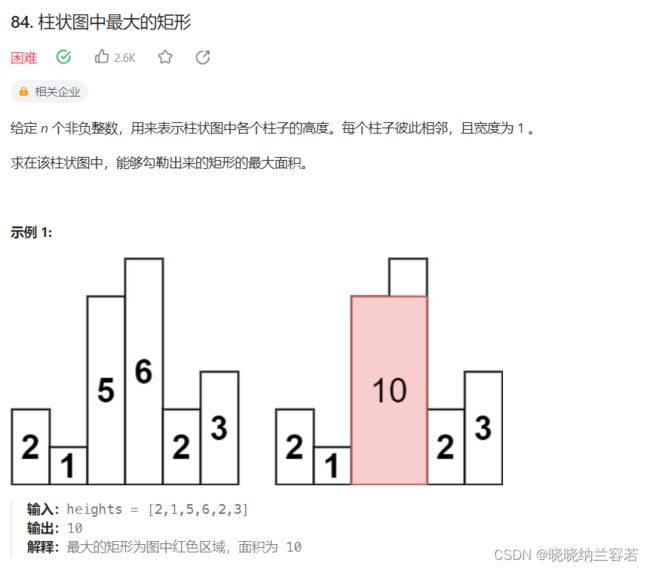
5--柱状图中最大的矩形

---

1--单调栈

        使用单调栈的特征：寻找第一个比当前元素大或者小的元素。

        当题目要求寻找左右第一个比当前栈顶元素大的元素时，使用单调递增的单调栈（从栈顶开始）；

        当题目要求寻找左右第一个比当前栈顶元素小的元素时，使用单调递减的单调栈（从栈顶开始）；

2--每日温度

主要思路：

        基于单调栈，单调栈从栈顶开始递增；单调栈存储的是元素对应的索引。

        当遇到一个元素大于栈顶元素i时，计算 answer[i]。

#include 
#include 
#include 

class Solution {
public:
    std::vector dailyTemperatures(std::vector& temperatures) {
        std::vector res(temperatures.size(), 0);
        std::stack stk;
        for(int i = 0; i < temperatures.size(); i++){
            while(!stk.empty() && temperatures[i] > temperatures[stk.top()]){
                res[stk.top()] = i - stk.top();
                stk.pop();
            }
            stk.push(i);
        }
        return res;
    }
};

int main(int argc, char* argv[]){
    // temperatures = [73,74,75,71,69,72,76,73]
    std::vector test = {73, 74, 75, 71, 69, 72, 76, 73};
    Solution S1;
    std::vector res = S1.dailyTemperatures(test);
    for(auto num : res) std::cout << num << " ";
    std::cout << std::endl;
    return 0;
}

3--下一个更大元素I

主要思路：

        基于单调栈和哈希表。

        将 nums1 的元素映射为哈希表，其中 key 为 num1[i]，val 为 i；

        遍历 nums2 构建单调栈，当 nums2[i] > stk.top() 时，且 stk.top() 属于 nums1，表明找到第一个比它大的元素，则根据hash_map[stk.top()]可以知道其在nums1的位置，记录结果res[hash_map[stk.top()]] = nums2[i] 即可。

#include 
#include 
#include 
#include 

class Solution {
public:
    std::vector nextGreaterElement(std::vector& nums1, std::vector& nums2) {
        std::vector res(nums1.size(), -1);
        if(nums1.size() == 0) return res;
        std::unordered_maphash_map;
        for(int i = 0; i < nums1.size(); i++) hash_map.emplace(nums1[i], i); // 存储值，索引

        std::stack stk;
        for(int i = 0; i < nums2.size(); i++){
            while(!stk.empty() && nums2[i] > stk.top()){
                if(hash_map.find(stk.top()) != hash_map.end()){
                    res[hash_map[stk.top()]] = nums2[i];
                }
                stk.pop();
            }
            stk.push(nums2[i]);
        }
        return res;
    }
};

int main(int argc, char* argv[]){
    // nums1 = [4,1,2], nums2 = [1,3,4,2]
    std::vector test1 = {4, 1, 2};
    std::vector test2 = {1, 3, 4, 2};
    Solution S1;
    std::vector res = S1.nextGreaterElement(test1, test2);
    for(auto num : res) std::cout << num << " ";
    std::cout << std::endl;
    return 0;
}

3--下一个更大元素II

主要思路：

        基于单调栈，本题的难点是针对一个循环数组，可以通过取模的操作来模拟循环数组。

#include 
#include 
#include 

class Solution {
public:
    std::vector nextGreaterElements(std::vector& nums) {
        std::vector res(nums.size(), -1);
        std::stack stk;
        for(int i = 0; i < 2*nums.size(); i++){
            // 通过取模操作模拟有环的过程
            int idx = i % nums.size();
            while(!stk.empty() && nums[idx] > nums[stk.top()]){
                res[stk.top()] = nums[idx];
                stk.pop();
            }
            stk.push(idx);
        }
        return res;
    }
};

int main(int argc, char* argv[]){
    // nums = [1, 2, 1]
    std::vector test = {1, 2, 1};
    Solution S1;
    std::vector res = S1.nextGreaterElements(test);
    for(int num : res) std::cout << num << " ";
    std::cout << std::endl;
    return 0;
}

4--接雨水

主要思路：

        维护一个单调递增的单调栈（从栈顶开始）。当某一个元素比当前栈顶元素大时，计算以该栈顶元素为中心的接雨水面积：area = （当前遍历元素的索引 - 栈顶元素栈中前一个元素的索引）* min(当前遍历元素的高度 - 栈顶元素的高度，栈顶元素栈中前一个元素的高度 - 栈顶元素的高度)

#include 
#include 
#include 

class Solution {
public:
    int trap(std::vector& height) {
        std::stack stk;
        int res = 0;
        for(int i = 0; i < height.size(); i++){
            while(!stk.empty() && height[i] > height[stk.top()]){
                int top_h = height[stk.top()]; // 栈顶元素高度
                stk.pop();
                if(!stk.empty()){
                    res += (i - stk.top() - 1) * std::min(height[i] - top_h, height[stk.top()] - top_h);
                }
            }
            stk.push(i);
        }
        return res;
    }
};

int main(int argc, char* argv[]){
    // height = [4, 2, 0, 3, 2, 5]
    std::vector test = {4, 2, 0, 3, 2, 5};
    Solution S1;
    int res = S1.trap(test);
    std::cout << res << std::endl;
    return 0;
}

5--柱状图中最大的矩形

主要思路：

        维护一个单调递减的单调栈（从栈顶开始），对于每一个柱子，寻找左右两边比其高度矮的柱子，计算其构成的矩形面积: area = （当前遍历元素的索引 - 栈顶元素在栈中上一个元素的索引 - 1）* 当前栈顶元素的高度；

#include 
#include 
#include 

class Solution {
public:
    int largestRectangleArea(std::vector& heights){
        int res = 0;
        std::stack stk;
        heights.insert(heights.begin(), 0);
        heights.insert(heights.end(), 0);
        for(int i = 0; i < heights.size(); i++){
            while(!stk.empty() && heights[i] < heights[stk.top()]){
                int cur_idx = stk.top();
                stk.pop();
                if(!stk.empty()){
                    res = std::max(res, (i - stk.top() - 1)*heights[cur_idx]);
                }
            }
            stk.push(i);
        }
        return res;
    }
};

int main(int argc, char* argv[]){
    // heights = [2, 1, 5, 6, 2, 3]
    std::vector test = {2, 1, 5, 6, 2, 3};
    Solution S1;
    int res = S1.largestRectangleArea(test);
    std::cout << res << std::endl;
    return 0;
}

代码随想录 ended in 2023.10.24 !!!