Flow-based models(NICE)；流模型+NICE+代码实现

参考：

1. 李宏毅春季机器学习
2. NICE: Non-linear Independent Components Estimation
3. https://github.com/gmum/nice_pytorch

大致思想

Flow-Based模型想要构造出一个可逆的模型，也就是说可以把图片正向输入得到一个向量，把这个向量反向输入就可以得到图片。
换句话说，Flow-Based模型是一个由输入的空间到输出的空间的双射。那么想要构造出这个双射，则需要一些数学上的知识。

数学预备知识

Jacobian矩阵

假设有这么一个函数，输入是一个向量，输出是一个向量，那么此时我们可以求这个函数的Jacobian矩阵：
y = f ( x ) J f = [ ∂ y 1 ∂ x 1 ∂ y 1 ∂ x 2 . . . ∂ y 1 ∂ x n ∂ y 2 ∂ x 1 ∂ y 2 ∂ x 2 . . . ∂ y 2 ∂ x n . . . ∂ y n ∂ x 1 ∂ y n ∂ x 2 . . . ∂ y n ∂ x n ] y=f(x)\\J_f=\begin{bmatrix} \frac{\partial y_1}{\partial x_1} & \frac{\partial y_1}{\partial x_2}...\frac{\partial y_1}{\partial x_n}\\ \frac{\partial y_2}{\partial x_1} & \frac{\partial y_2}{\partial x_2}...\frac{\partial y_2}{\partial x_n}\\ ...\\ \frac{\partial y_n}{\partial x_1} & \frac{\partial y_n}{\partial x_2}...\frac{\partial y_n}{\partial x_n} \end{bmatrix} y=f(x)Jf​= ​∂x1​∂y1​​∂x1​∂y2​​...∂x1​∂yn​​​∂x2​∂y1​​...∂xn​∂y1​​∂x2​∂y2​​...∂xn​∂y2​​∂x2​∂yn​​...∂xn​∂yn​​​ ​
上面就是Jacobian矩阵，其中我们假设x和y都是n维向量。

假设f可逆，也就是$f^{-1}(y)=x$，那么此时Jacobian矩阵有这么一个性质：
$$J_{f^{-1}}=J_f^{-1}$$
也就是说该函数的反函数的Jacobian矩阵是原函数的Jacobian矩阵的逆矩阵。

行列式以及其几何意义

行列式线性代数都学过，举例来说，二阶行列式可以这么算：
∣ a b c d ∣ = a d − c b \left | \begin{matrix}a & b\\ c & d\end{matrix} \right | = ad - cb ​ac​bd​ ​=ad−cb
这个行列式的几何意义如下：

如上，把二阶行列式的两个行向量在坐标轴上画出，然后构造出平行四边形。那么这个平行四边形的面积就是行列式的值。

Change of Variable Theorem

假设有两个分布记做$\pi (z),p(x)$以及他们两个分布之间的变换函数$x=f(z)$

如上图，也就是说给定上面的一个z’则对应下面p分布中的一个x’。而对应的函数的得值分别是$\pi (z^{\prime }),p(x^{\prime })$

假设，在z’上取一个很小的变动，记做$\Delta z$那么此时，就会得到一个区间$[z,z+\Delta z]$，那么此时对应的x’也会有一个变化区间，由于这个区间过于小，所以可以近似当做是一个矩形。可以证明，此时两个矩形的面积是一致的：

此时就有
$$\pi (z^{\prime })\Delta z=p(x^{\prime })\Delta x\to \pi (z^{\prime })=p(x^{\prime })\frac{\Delta z}{\Delta x}\approx p(x^{\prime })\frac{dz}{dx}$$
当这个区间足够小时，就可以近似微为微分。
由于有时变化反向肯能不一致，所以要加一个绝对值：
$$\pi (z^{\prime })=p(x^{\prime })|\frac{dz}{dx}|$$
如果换成二维分布，则可以得到：

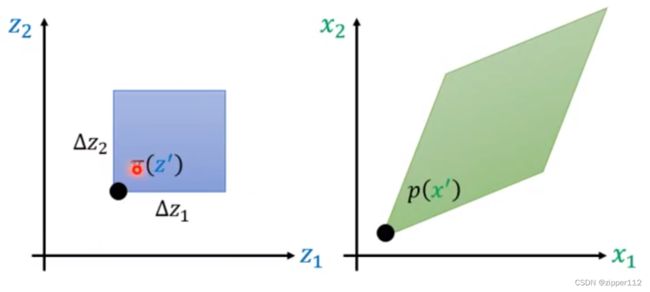
此时就会得到：

然后仿照上述的步骤进行变换，就可以得到：

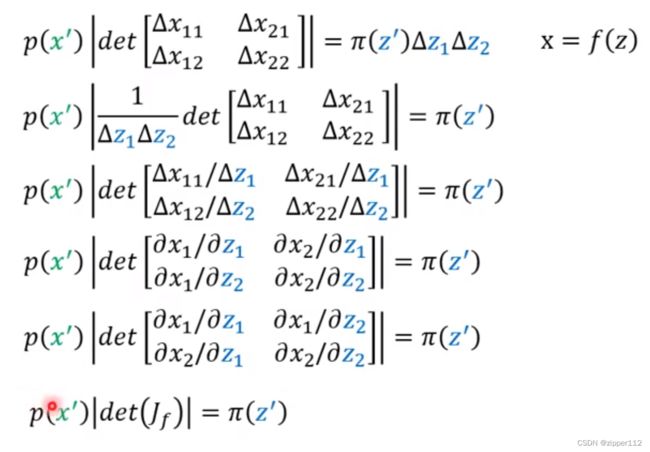
于是我们就得到了这么一个关系：
$$\begin{gathered} p(x^{\prime })|det(J_f)|=\pi (z^{\prime }) \\ p(x^{\prime })=\pi (z^{\prime })|det(J_{f^{-1}})| \end{gathered}$$

Flow-based model

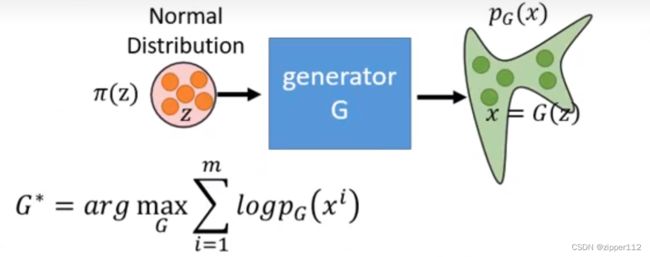
如上图所示，生成模型的目标在于，对样本所在的目标分布$P_{data}(x)$进行建模。
我们通常的做法是，输入一个已知的分布$\pi (z)$，例如标准高斯分布。然后通过一个神经网络，学到一个变换关系，把这个分布变换成$P_G(x)$，最后我们期望这个最终的分布和目标的分布$P_{data}(x)$尽可能的接近。

此时一个常见的做法就是进行最大似然估计，可以证明最大似然估计等同于最小化$D_{KL}(P_G||P_{data})$。
根据上述的公式，我们其实已经知道了$z,x$的关系，于是就有

然后再加上一个对数就得到：
$$log(p_G(x^i))=log(\pi (z^i))+log(|det(J_{G^{-1}})|)$$

因为要求可逆，所以要求特殊的神经网络。但是我们可以选择一些简单的网络像流一样把它们整合起来：

于是就有了如下的公式
$$log{p}_k(x^i)=log\pi (z^i)+\sum _{i=1}^{k}log|det(J_{G_i^{-1}})|$$
我们在实际训练的时候，训练的是$G^{-1}$，因为此时我们手上有的是$P_{data}(x)$中采样的数据。
$$z^i=G^{-1}(x^i)$$
在训练结束后，反过来就可以做生成了。

NICE

理论

首先，对于输入z，我们我们把其分为两个部分，记做$[x_1,x_2]$其中这两个部分不重叠。例如我们可以把前k个元素记做$x_1$剩下的记做$x_2$。
此时NICE的操作如下：
$$\begin{gathered} h_1^1=x_1 \\ {h}_2^1=x_2+m_1(x_1) \end{gathered}$$
其中m1是一个非线性的变换函数。此时$[h_1^1,h_2^1]$就是我们NICE第一层的输出了。
也就是说，我们首先对第一部分进行了直接复制，第二部分的输出则是由第二部分加上一个第一部分的非线性变换组成的。

假设NICE只有一层，那么$h^1=[h_1^1,h_2^1]$就是最终输出了，可以看到整个计算过程是可逆的。也就是说反过来我们可以由$h^1$得到$[x_1,x_2]$。

我们把这一层的输出进行一下位置调转，输入到下一层，然后反复地重复这个步骤，就可以得到最终的NICE网络：

接下来我们来计算这个操作的Jacobian矩阵，如下：

可以得到其det为1。同理，后面每一层的det都是1。

假设先验分布z是高斯分布，则
$$\begin{gathered} log(p_G(x))=log\pi (z^i)+\sum _{i=1}^{k}log|det(J_{G_i^{-1}})| \\ =log\pi (f(x^i))+\sum _{i=1}^{k}log|det(J_{G_i^{-1}})| \\ \approx -\frac{1}{2}||f(x^i)|{|}^2+\sum _{i=1}^{k}log|det(J_{G_i^{-1}})| \\ =-\frac{1}{2}||f(x^i)|{|}^2(带入行列式) \end{gathered}$$

此时还存在一个问题，那就是输入的图片大多都是稀疏的，也就是说某些维度空间可能并不重要。所以作者在最后加上了一个尺度变换的可学习向量s。
$$h^n\otimes s$$
此时最后一层的det不再是1了，仔细计算之后就会发现他变成了：
$$\sum _i{s}_i$$
于是我们损失函数变成：
$$-\frac{1}{2}||f(x^i)\otimes s|{|}^2+\sum _i{s}_i$$

代码

注意，代码中的划分方式改成了奇偶划分，也就是按照奇偶的方式选择谁是$x_1,x_2$

import torch
import torch.nn as nn
import torch.nn.init as init


_get_even = lambda xs: xs[:,0::2]
_get_odd = lambda xs: xs[:,1::2]

def _interleave(first, second, order):
    """
    交叉的还原h
    """
    cols = []
    if order == 'even':
        for k in range(second.shape[1]):
            cols.append(first[:,k])
            cols.append(second[:,k])
        if first.shape[1] > second.shape[1]:
            cols.append(first[:,-1])
    else:
        for k in range(first.shape[1]):
            cols.append(second[:,k])
            cols.append(first[:,k])
        if second.shape[1] > first.shape[1]:
            cols.append(second[:,-1])
    return torch.stack(cols, dim=1)


class AdditiveCouplingLayer(nn.Module):
    def __init__(self, dim, partition, nonlinearity):
        """
        dim: 特征维度
        partition: 切分方式（first是奇数还是偶数）
        nonlinearity: 非线性函数
        """
        super(AdditiveCouplingLayer, self).__init__()
        self.dim = dim
        assert (partition in ['even', 'odd']), "错误，不存在这种切分方式" # 切分方式
        self.partition = partition
        if (partition == 'even'):
            self._first = _get_even
            self._second = _get_odd
        else:
            self._first = _get_odd
            self._second = _get_even

        self.add_module('nonlinearity', nonlinearity) # 注册非线性函数

    def forward(self, x): # forward过程，计算first和second，并且拼接
        return _interleave(
            self._first(x),
            self.coupling_law(self._second(x), self.nonlinearity(self._first(x))),
            self.partition
        )

    def inverse(self, y):# backward过程，同forward过程，但是是相减
        """Inverse mapping through the layer. Gradients should be turned off for this pass."""
        return _interleave(
            self._first(y),
            self.anticoupling_law(self._second(y), self.nonlinearity(self._first(y))),
            self.partition
        )

    def coupling_law(self, a, b):
        return a + b

    def anticoupling_law(self, a, b):
        return a - b

    
def _build_relu_network(latent_dim, hidden_dim, num_layers): # 非线性函数m
    _modules = [ nn.Linear(latent_dim, hidden_dim) ]
    for _ in range(num_layers):
        _modules.append( nn.Linear(hidden_dim, hidden_dim) )
        _modules.append( nn.ReLU() )
        _modules.append( nn.BatchNorm1d(hidden_dim) )
    _modules.append( nn.Linear(hidden_dim, latent_dim) )
    return nn.Sequential( *_modules )

class NICEModel(nn.Module):
    def __init__(self, input_dim, hidden_dim, num_layers):
        super(NICEModel, self).__init__()
        assert (input_dim % 2 == 0), "由于是奇偶切分，特征维度必须是否书"

        self.input_dim = input_dim
        half_dim = int(input_dim / 2)
        # 交叉的插入AdditiveCouplingLayer层，相当于上面说的调换位置
        self.layer1 = AdditiveCouplingLayer(input_dim, 'odd', _build_relu_network(half_dim, hidden_dim, num_layers)) 
        self.layer2 = AdditiveCouplingLayer(input_dim, 'even', _build_relu_network(half_dim, hidden_dim, num_layers)) # 
        self.layer3 = AdditiveCouplingLayer(input_dim, 'odd', _build_relu_network(half_dim, hidden_dim, num_layers))
        self.layer4 = AdditiveCouplingLayer(input_dim, 'even', _build_relu_network(half_dim, hidden_dim, num_layers))
        self.scaling_diag = nn.Parameter(torch.ones(input_dim)) # 设置一个尺度变换的向量

        # 初始化各个参数
        for p in self.layer1.parameters():
            if len(p.shape) > 1:
                init.kaiming_uniform_(p, nonlinearity='relu')
            else:
                init.normal_(p, mean=0., std=0.001)
        for p in self.layer2.parameters():
            if len(p.shape) > 1:
                init.kaiming_uniform_(p, nonlinearity='relu')
            else:
                init.normal_(p, mean=0., std=0.001)
        for p in self.layer3.parameters():
            if len(p.shape) > 1:
                init.kaiming_uniform_(p, nonlinearity='relu')
            else:
                init.normal_(p, mean=0., std=0.001)
        for p in self.layer4.parameters():
            if len(p.shape) > 1:
                init.kaiming_uniform_(p, nonlinearity='relu')
            else:
                init.normal_(p, mean=0., std=0.001)        


    def forward(self, xs):
        # 前向计算，正常的算就行
        ys = self.layer1(xs)
        ys = self.layer2(ys)
        ys = self.layer3(ys)
        ys = self.layer4(ys)
        ys = torch.matmul(ys, torch.diag(torch.exp(self.scaling_diag))) # 最后乘以尺度变换向量
        return ys


    def inverse(self, ys):
        with torch.no_grad():
            xs = torch.matmul(ys, torch.diag(torch.reciprocal(torch.exp(self.scaling_diag)))) # 除以s
            xs = self.layer4.inverse(xs) # 反向计算
            xs = self.layer3.inverse(xs)
            xs = self.layer2.inverse(xs)
            xs = self.layer1.inverse(xs)
        return xs