八位超前进位加法器&八位行波进位加法器

八位超前进位加法器

原理

有学弟问我，超前进位加法器中的p=add1 ^ add2和g=add1 & add2是什么意思，所以这篇文章就稍微赘述一点吧~

所谓超前进位，首先应该明白进位是什么。

8+4=12，其中的1就是进位，其中的2才是结果。

那么在二进制中，1+1=10，其中的1就是进位，0就是结果。

明白了进位和结果，那么多位的数字是怎么计算呢？

其实上面的计算应该是1+1+上一位的进位=10，所以两个数字的计算应该涉及三个内容——加数，被加数，上一位的进位。

在一位二进制加法中，a和b分别表示两个加数，cin表示上一位的进位，cout表示下一位的进位，sum表示结果，我们列出其真值表：

add1	add2	cin	cout	sum
0	0	0	0	0
0	1	0	0	1
1	0	0	0	1
1	1	0	1	0
0	0	1	0	1
0	1	1	1	0
1	0	1	1	0
1	1	1	1	1

以数字**1为真**，数字**0为假**，a表示1，a'表示0，这样的形式。学过离散数学或者数字电路的同学应该多少会点吧，“·”代表“与”，“+”代表“或”，所以上面的真值表，写成表达式，就是：
$$cout=add1\cdot add2\cdot ci{n}^{\prime }+add{1}^{\prime }\cdot add2\cdot cin+add1\cdot add{2}^{\prime }cin+add1\cdot add2\cdot cin$$
经过部分化简：
$$cout=add1\cdot add2+add{1}^{\prime }add2\cdot cin+add1\cdot add{2}^{\prime }\cdot cin=add1\cdot add2+cin\cdot (add1\oplus add2)$$
同理：
$$sum=add1\oplus add2\oplus cin$$
找到两个等式的相同部分，都有a⊕b，其中⊕代表“异或”，在Verilog中用“^”表示，即a^b，所以令p = add1 ^ add2，现在知道干什么用的了嘛？

没错，就是中间变量而已，同理g = add1 & add2也是中间变量，这样就可以把上面两个等式改写成：cout = g | (cin & p)和sum = add1 ^ add2 ^ cin（其实就是变短了一点点而已）

不过呢，适当的使用中间变量，可能会让你的代码精简许多~

此外，我发现一个网站可以通过真值表生成表达式：http://www.32x8.com/index.html

设计文件

module add_8_1(
    input wire [7:0] add1,
    input wire [7:0] add2,
    input wire cin,
    output wire [7:0] sum,
    output wire cout
    );
    wire[7:0] g,p,c;//g和p的含义已经讲解了，c代表每一位计算的进位，c[0]表示原始的进位cin
    assign c[0]=cin;
    assign p=add1 ^ add2;
    assign g=add1 & add2;
    assign c[0] = g[0] | (p[0] & c[0]);
    assign c[1] = g[1] | (p[1] & (g[0] | (p[0] & c[0])));
    assign c[2] = g[2] | (p[2] & (g[1] | (p[1] & (g[0] | (p[0] & c[0])))));
    assign c[3] = g[3] | (p[3] & (g[2] | (p[2] & (g[1] | (p[1] & (g[0] | (p[0] & c[0])))))));
    assign c[4] = g[4] | (p[4] & (g[3] | (p[3] & (g[2] | (p[2] & (g[1] | (p[1] & (g[0] | (p[0] & c[0])))))))));
    assign c[5] = g[5] | (p[5] & (g[4] | (p[4] & (g[3] | (p[3] & (g[2] | (p[2] & (g[1] | (p[1] & (g[0] | (p[0] & c[0])))))))))));
    assign c[6] = g[6] | (p[6] & (g[5] | (p[5] & (g[4] | (p[4] & (g[3] | (p[3] & (g[2] | (p[2] & (g[1] | (p[1] & (g[0] | (p[0] & c[0])))))))))))));
    assign c[7] = g[7] | (p[7] & (g[6] | (p[6] & (g[5] | (p[5] & (g[4] | (p[4] & (g[3] | (p[3] & (g[2] | (p[2] & (g[1] | (p[1] & (g[0] | (p[0] & c[0])))))))))))))));
    assign sum=p^c[7:0];
    assign cout=c[7];
endmodule

上面的代码应该看起来很长，像老太太的裹脚布，但这也就是所谓的超前进位。

Verilog中“块”和assign语句都是并行执行的，上面有许多assign语句，所以从c[0]到c[7]，根据第一步的cin，就可以同步计算出每一位的进位（超前进位），以及最后的结果，这些是同时完成的，也就完成了超前进位加法器。

综合电路

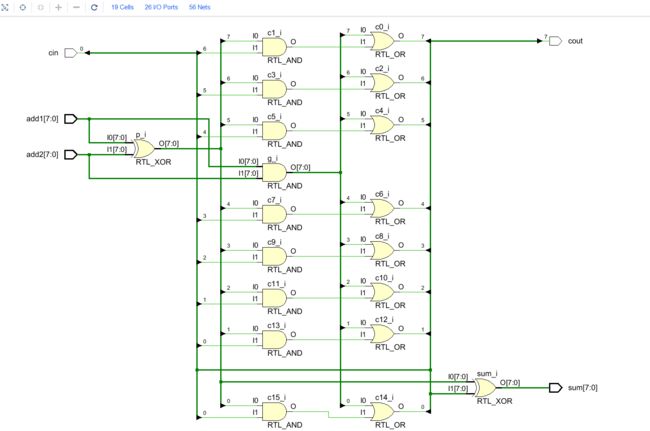
点击RTL-ANALYSIS——Synthesis，可以查看综合电路图：

19个元件，26个IO口，56根线

测试文件

`timescale 1ns / 1ps
module add_tb();
    reg [7:0] add1,add2;
    reg cin;
    reg clk;
    wire [7:0] sum;
    wire cout;
    initial begin
        add1 <= 8'd10;
        add2 <= 8'd3;
        cin <= 1'b0;     
        clk <= 1'b0;   
    end
    
    always # 10 clk = ~clk;
    always @ (negedge clk) begin
        {add1,add2} <= {add1,add2} + 1'b1;
    end

    add_8_1 try(.add1(add1),.add2(add2),.cin(cin),.sum(sum),.cout(cout));
    
endmodule

还有些同学，对测试文件的理解也还是不够深刻，这里稍提一嘴，测试文件就是给电路加激励信息，使电路运作。至于加提示信息之类的，各自加油就好啦~

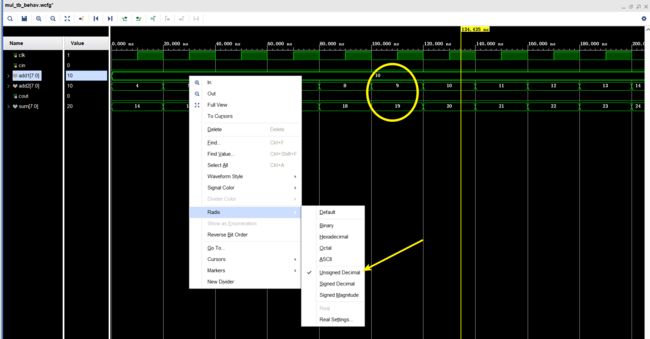
仿真波形

右键某一信号，选择相应的进制数，以10+9为例，最终输出cout=0，sum=19

那么之后的10+11为什么没有进位使cout=1呢？

把他们转换成二进制观察一下就明白啦~

八位行波进位加法器

当时不知道在哪听的这个名字，就一直用下了，其实这个应该叫做行波进位加法器——由N个全加器级联而成，所以被我叫成了级联进位emmm

原理

如上所说，行波进位加法器是由N个全加器级联而成，比如8位的加法器可以由8个一位全加器级联而成，也可以由2个四位全加器构成，区别就是所综合出的电路大小。

设计文件

方式一

module add_8_2(
    input wire [7:0] add1,add2,
    input wire cin,
    output reg [7:0] sum,
    output reg cout
);
    reg[7:0] G,P,C; 
always @(add1 or add2 or cin)
begin
    G[0] = add1[0] & add2[0]; 
    P[0] = add1[0] ^ add2[0]; 
    C[0] = cin; //最低位的进位输入，即cin
    sum[0] = G[0]^ P[0] ^ C[0];//第一位的计算结果
    G[1] = add1[1] & add2[1];
    P[1] = add1[1] ^ add2[1];
    C[1] = G[0] |(P[0] & C[0]);//c=add1add2+(add1+add2)cin=G|(P&cin)
    sum[1] = G[1] ^ P[1] ^ C[1];
    G[2] = add1[2] & add2[2];
    P[2] = add1[2] ^ add2[2];
    C[2] = G[1] |(P[1] & C[1]);
    sum[2] = G[2] ^ P[2] ^ C[2];
    G[3] = add1[3]& add2[3];
    P[3] = add1[3] ^ add2[3];
    C[3] = G[2] |(P[2] & C[2]);
    sum[3] = G[3] ^ P[3] ^ C[3];
    G[4] = add1[4] & add2[4];
    P[4] = add1[4] ^ add2[4];
    C[4] = G[3] |(P[3] & C[3]);
    sum[4] = G[4] ^ P[4] ^ C[4];
    G[5] = add1[5] & add2[5];
    P[5] = add1[5] ^ add2[5];
    C[5] = G[4] |(P[4] & C[4]);
    sum[5] = G[5] ^ P[5] ^ C[5];
    G[6] = add1[6] & add2[6];
    P[6] = add1[6] ^ add2[6];
    C[6] = G[5] |(P[5] & C[5]);
    sum[6] = G[6] ^ P[6] ^ C[6];
    G[7] = add1[7] & add2[7];
    P[7] = add1[7] ^ add2[7];
    C[7] = G[6] |(P[6] & C[6]);
    sum[7] = G[7] ^ P[7] ^ C[7];
    cout = G[7] |(P[7] & C[7]);
end
endmodule

这是把上述原理复现了一边，上一步的进位输出，传入到下一位计算的进位输入。

综合后的电路如下，48个元件，26个IO口，65根线

综合电路

方式二

上面的语句重复性太大，就用模块例化的方式来写

module add_8_2(
    input wire [7:0] add1,add2,
    input wire cin,
    output wire [7:0] sum,
    output wire cout
);
    wire [6:0] c;
    add_1_unit a1(add1[0],add2[0],cin,c[0],sum[0]);
    add_1_unit a2(add1[1],add2[1],c[0],c[1],sum[1]);
    add_1_unit a3(add1[2],add2[2],c[1],c[2],sum[2]);
    add_1_unit a4(add1[3],add2[3],c[2],c[3],sum[3]);
    add_1_unit a5(add1[4],add2[4],c[3],c[4],sum[4]);
    add_1_unit a6(add1[5],add2[5],c[4],c[5],sum[5]);
    add_1_unit a7(add1[6],add2[6],c[5],c[6],sum[6]);
    add_1_unit a8(add1[7],add2[7],c[6],cout,sum[7]);
endmodule

其中的add_1_unit模块如下：

module add_1_unit(
    input wire add1,add2,cin,
    output wire cout,sum
    );
    assign cout = (add1 & add2) | (cin & (add1 ^ add2));
    assign sum = add1 ^ add2 ^ cin;    
endmodule

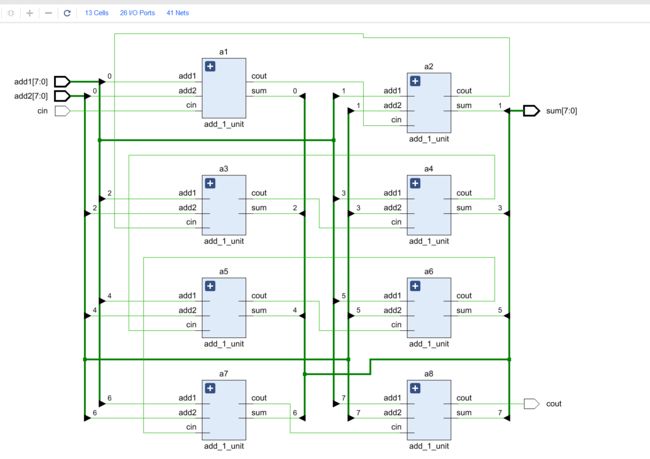
综合后的电路如下，全展开后有48个元件，26个IO口，97根线

综合电路

其中的每一个单元如下：

全展开后如下：

两种写法

数据总线的数量有区别：一个是65根线，一个是97根线。

代码量有区别：一个40行左右，一个总共27行左右。

优缺点不言而喻。

测试文件

都是八位加法器，与超前进位加法器也没区别

还是放一下吧：

`timescale 1ns / 1ps
module add_tb();
    reg [7:0] add1,add2;
    reg cin;
    reg clk;
    wire [7:0] sum;
    wire cout;
    initial begin
        add1 <= 8'd10;
        add2 <= 8'd3;
        cin <= 1'b0;     
        clk <= 1'b0;   
    end
    
    always # 10 clk = ~clk;
    always @ (negedge clk) begin
        {add1,add2} <= {add1,add2} + 1'b1;
    end

    add_8_2 try(.add1(add1),.add2(add2),.cin(cin),.sum(sum),.cout(cout));
    
endmodule

仿真波形

与超前进位一致，用二进制查看一下如下图：

总结

行波进位加法器，由于后一位的进位依赖于前一位的进位，所以关键路径更长，限制速度，性能不高，

超前进位加法器，由于进位计算是并行的，所以关键路径短，速度快，但是位宽越宽，也就代表会综合出更复杂的、面积更大的电路。