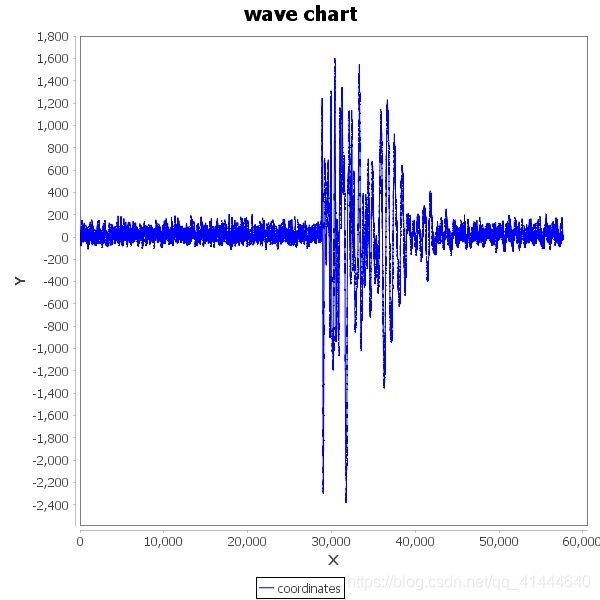
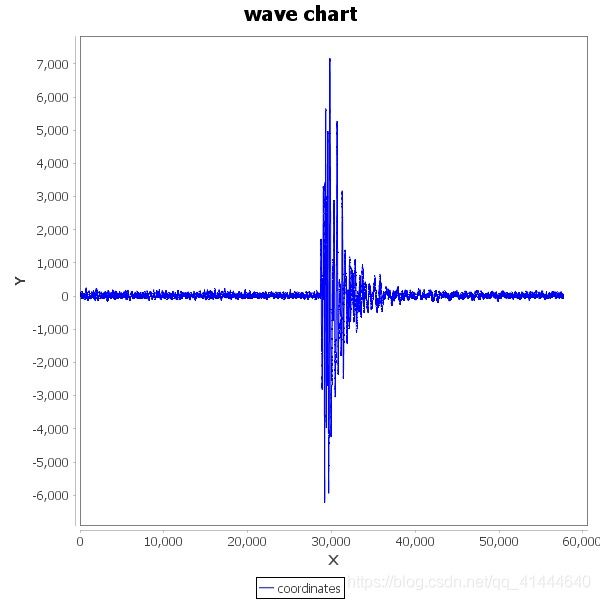
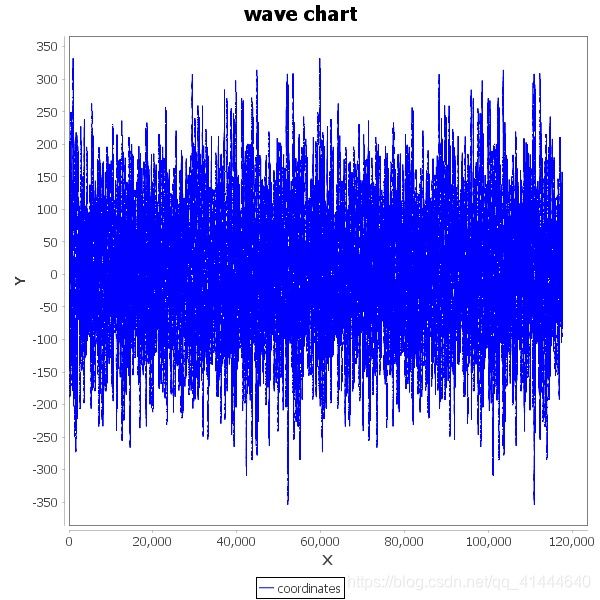
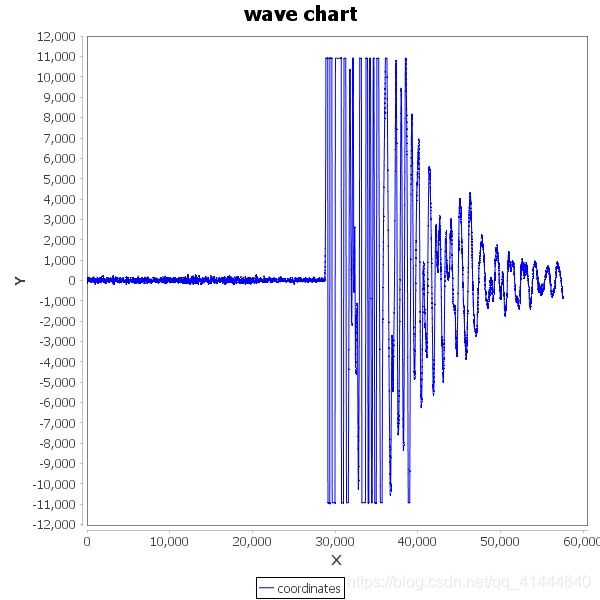
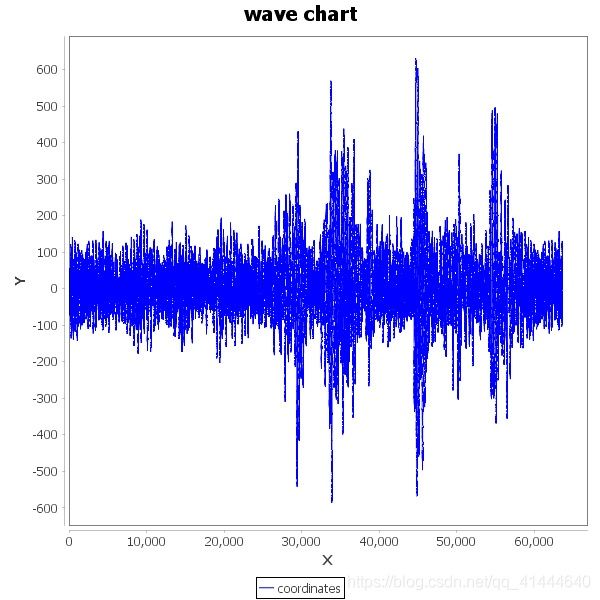
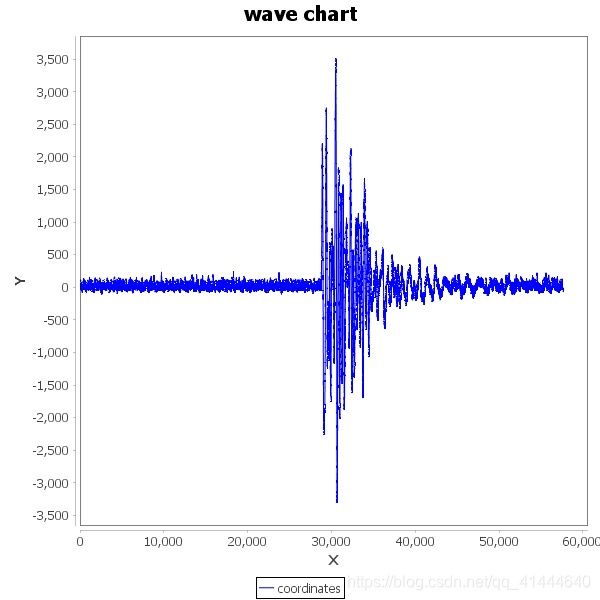
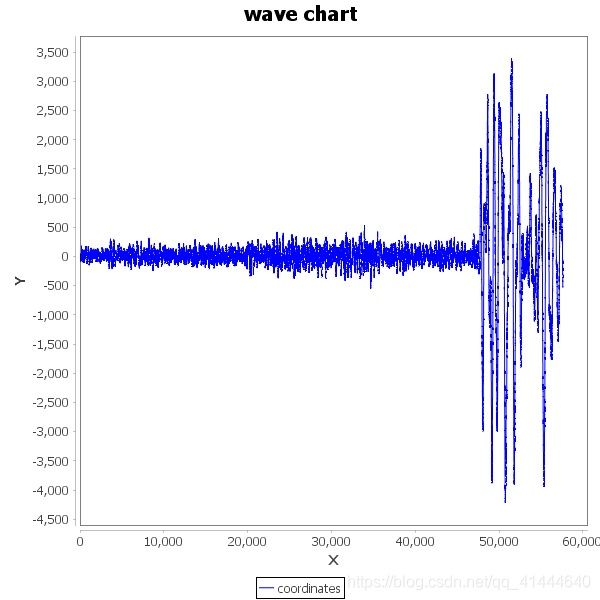
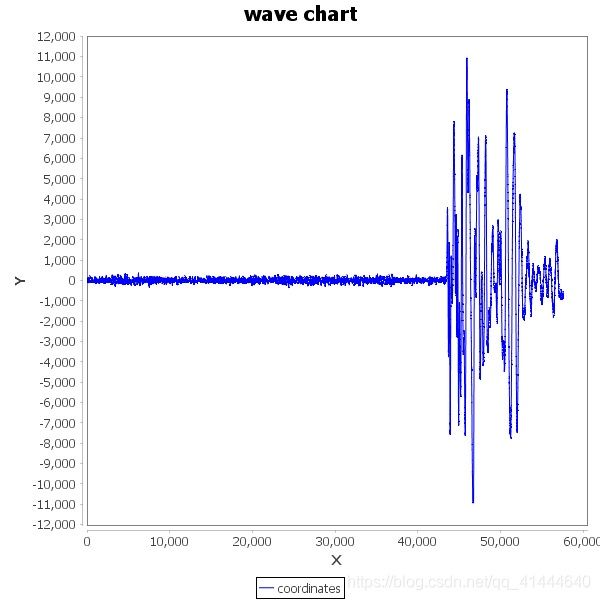
聚类分析

一、概念

1、DTW

(1)引入

【DTW部分转载自https://blog.csdn.net/zouxy09/article/details/9140207】
在大部分的学科中，时间序列是数据的一种常见表示形式。对于时间序列处理来说，一个普遍的任务就是比较两个序列的相似性。

在时间序列中，我们通常需要比较两端音频的差异。而这两段音频的长度大部分是不相等的。在语音处理领域上表现为不同人的语速不同。即时同一个人不同一时刻发同一个音，也不可能具有完全相同的时间长度。而且每个人对同一个单词的不同音素的发音速度也是不同的，有的人会把"A"这个音拖得稍长，或者"i"稍短。在这种复杂的情况下，利用传统的欧几里得距离是无法求得有效的两个时间序列之间的相似性的（即距离）。

例如图A所示，实线和虚线分别是同一个词“pen”的两个语音波形（在y轴上拉开了，以便观察）。可以看到他们整体上的波形形状很相似，但在时间轴上却是不对齐的。例如在第20个时间点的时候，实线波形的a点会对应于虚线波形的b’点，这样传统的通过比较距离来计算相似性很明显不靠谱。因为很明显，实线的a点对应虚线的b点才是正确的。而在图B中，DTW就可以通过找到这两个波形对齐的点，这样计算它们的距离才是正确的。

也就是说，大部分情况下，两个序列整体上具有非常相似的形状，但是这些形状在x轴上并不是对齐的。所以我们在比较他们的相似度之前，需要将其中一个（或者两个）序列在时间轴下warping扭曲，以达到更好的对齐。而DTW就是实现这种warping扭曲的一种有效方法。DTW通过把时间序列进行延伸和缩短，来计算两个时间序列性之间的相似性。

​ 那如果才知道两个波形是对齐了呢？也就是说怎么样的warping才是正确的？直观上理解，当然是warping一个序列后可以与另一个序列重合recover。这个时候两个序列中所有对应点的距离之和是最小的。所以从直观上理解，warping的正确性一般指“feature to feature”的对齐。

(2)DTW（Dynamic Time Warping，动态时间归整）

动态时间规整DTW是一个典型的优化问题，它用满足一定条件的的时间规整函数W(n)描述测试模板和参考模板的时间对应关系，求解两模板匹配时累计距离最小所对应的规整函数。

假设我们有两个时间序列Q和C，他们的长度分别是n和m：（实际语音匹配运用中，一个序列为参考模板，一个序列为测试模板，序列中的每个点的值为语音序列中每一帧的特征值。例如语音序列Q共有n帧，第i帧的特征值（一个数或者一个向量）是qi。至于取什么特征，在这里不影响DTW的讨论。我们需要的是匹配这两个语音序列的相似性，以达到识别我们的测试语音是哪个词）

Q = q1, q2,…,qi,…, qn ;

C = c1, c2,…, cj,…, cm ;

​ 如果n=m，那么就用不着折腾了，直接计算两个序列的距离就好了。但如果n不等于m我们就需要对齐。最简单的对齐方式就是线性缩放了。把短的序列线性放大到和长序列一样的长度再比较，或者把长的线性缩短到和短序列一样的长度再比较。但是这样的计算没有考虑到语音中各个段在不同情况下的持续时间会产生或长或短的变化，因此识别效果不可能最佳。因此更多的是采用动态规划（dynamic programming）的方法。

为了对齐这两个序列，我们需要构造一个n x m的矩阵网格，矩阵元素(i, j)表示qi和cj两个点的距离d(qi, cj)（也就是序列Q的每一个点和C的每一个点之间的相似度，距离越小则相似度越高。这里先不管顺序），一般采用欧式距离，d(qi, cj)= (qi-cj)2（也可以理解为失真度）。每一个矩阵元素(i, j)表示点qi和cj的对齐。DP算法可以归结为寻找一条通过此网格中若干格点的路径，路径通过的格点即为两个序列进行计算的对齐的点。

那么这条路径我们怎么找到呢？那条路径才是最好的呢？也就是刚才那个问题，怎么样的warping才是最好的。

我们把这条路径定义为warping path规整路径，并用W来表示， W的第k个元素定义为wk=(i,j)k，定义了序列Q和C的映射。这样我们有：

首先，这条路径不是随意选择的，需要满足以下几个约束：

1）边界条件：w1=(1, 1)和wK=(m, n)。任何一种语音的发音快慢都有可能变化，但是其各部分的先后次序不可能改变，因此所选的路径必定是从左下角出发，在右上角结束。

2）连续性：如果wk-1= (a’, b’)，那么对于路径的下一个点wk=(a, b)需要满足 (a-a’) <=1和 (b-b’) <=1。也就是不可能跨过某个点去匹配，只能和自己相邻的点对齐。这样可以保证Q和C中的每个坐标都在W中出现。

3）单调性：如果wk-1= (a’, b’)，那么对于路径的下一个点wk=(a, b)需要满足0<=(a-a’)和0<= (b-b’)。这限制W上面的点必须是随着时间单调进行的。以保证图B中的虚线不会相交。

​ 结合连续性和单调性约束，每一个格点的路径就只有三个方向了。例如如果路径已经通过了格点(i, j)，那么下一个通过的格点只可能是下列三种情况之一：(i+1, j)，(i, j+1)或者(i+1, j+1)。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-0HoIgHNH-1610547993779)(.images/20130620200949125.jpg)]

满足上面这些约束条件的路径可以有指数个，然后我们感兴趣的是使得下面的规整代价最小的路径：

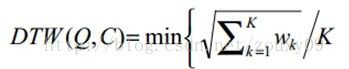
分母中的K主要是用来对不同的长度的规整路径做补偿。我们的目的是什么？或者说DTW的思想是什么？是把两个时间序列进行延伸和缩短，来得到两个时间序列性距离最短也就是最相似的那一个warping，这个最短的距离也就是这两个时间序列的最后的距离度量。在这里，我们要做的就是选择一个路径，使得最后得到的总的距离最小。

这里我们定义一个累加距离cumulative distances。从(0, 0)点开始匹配这两个序列Q和C，每到一个点，之前所有的点计算的距离都会累加。到达终点(n, m)后，这个累积距离就是我们上面说的最后的总的距离，也就是序列Q和C的相似度。

累积距离γ(i,j)可以按下面的方式表示，累积距离γ(i,j)为当前格点距离d(i,j)，也就是点qi和cj的欧式距离（相似性）与可以到达该点的最小的邻近元素的累积距离之和：

最佳路径是使得沿路径的积累距离达到最小值这条路径。这条路径可以通过动态规划（dynamic programming）算法得到。

补充：

现在我们用一个6*6矩阵M表示序列A（1-1-3-3-2-4）和序列B（1-3-2-2-4-4）各个点之间的距离，M(i, j)等于A的第i个点和B的第j个点之间的距离，即

因此，DTW算法的步骤为：

1. 计算两个序列各个点之间的距离矩阵。

2. 寻找一条从矩阵左上角到右下角的路径，使得路径上的元素和最小。
   
   

2、Kmeans

(1)引入

【K-means部分转载自：https://blog.csdn.net/sinat_36710456/article/details/88019323】
**分类：**分类其实是从特定的数据中挖掘模式，作出判断的过程。比如Gmail邮箱里有垃圾邮件分类器，一开始的时候可能什么都不过滤，在日常使用过程中，我人工对于每一封邮件点选“垃圾”或“不是垃圾”，过一段时间，Gmail就体现出一定的智能，能够自动过滤掉一些垃圾邮件了。这是因为在点选的过程中，其实是给每一条邮件打了一个“标签”，这个标签只有两个值，要么是“垃圾”，要么“不是垃圾”，Gmail就会不断研究哪些特点的邮件是垃圾，哪些特点的不是垃圾，形成一些判别的模式，这样当一封信的邮件到来，就可以自动把邮件分到“垃圾”和“不是垃圾”这两个我们人工设定的分类的其中一个。

**聚类：**聚类的目的也是把数据分类，但是事先我是不知道如何去分的，完全是算法自己来判断各条数据之间的相似性，相似的就放在一起。在聚类的结论出来之前，我完全不知道每一类有什么特点，一定要根据聚类的结果通过人的经验来分析，看看聚成的这一类大概有什么特点。

聚类和分类最大的不同在于：分类的目标是事先已知的，而聚类则不一样，聚类事先不知道目标变量是什么，类别没有像分类那样被预先定义出来。

(2)K-Means

聚类算法有很多种（几十种），K-Means是聚类算法中的最常用的一种，算法最大的特点是简单，好理解，运算速度快，但是只能应用于连续型的数据，并且一定要在聚类前需要手工指定要分成几类。

下面，我们描述一下K-means算法的过程，为了尽量不用数学符号，所以描述的不是很严谨，大概就是这个意思，“物以类聚、人以群分”：

1. 首先输入k的值，即我们希望将数据集经过聚类得到k个分组。

2. 从数据集中随机选择k个数据点作为初始大哥（质心，Centroid）

3. 对集合中每一个小弟，计算与每一个大哥的距离（距离的含义后面会讲），离哪个大哥距离近，就跟定哪个大哥。

4. 这时每一个大哥手下都聚集了一票小弟，这时候召开人民代表大会，每一群选出新的大哥（其实是通过算法选出新的质心）。

5. 如果新大哥和老大哥之间的距离小于某一个设置的阈值（表示重新计算的质心的位置变化不大，趋于稳定，或者说收敛），可以认为我们进行的聚类已经达到期望的结果，算法终止。

6. 如果新大哥和老大哥距离变化很大，需要迭代3~5步骤。

例：我搞了6个点，从图上看应该分成两推儿，前三个点一堆儿，后三个点是另一堆儿。现在手工执行K-Means，体会一下过程，同时看看结果是不是和预期一致。

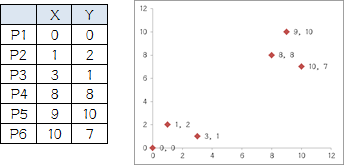
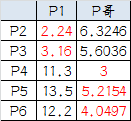
1.选择初始大哥： 我们就选P1和P2

2.计算小弟和大哥的距离： P3到P1的距离从图上也能看出来（勾股定理），是√10 = 3.16；P3到P2的距离√((3-1)^2+(1-2)2 = √5 = 2.24，所以P3离P2更近，P3就跟P2混。同理，P4、P5、P6也这么算，如下：

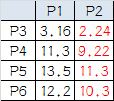
round1:

P3到P6都跟P2更近，所以第一次站队的结果是：

• 组A：P1

• 组B：P2、P3、P4、P5、P6

3.人民代表大会： 组A没啥可选的，大哥还是P1自己 组B有五个人，需要选新大哥，这里要注意选大哥的方法是每个人X坐标的平均值和Y坐标的平均值组成的新的点，为新大哥，也就是说这个大哥是“虚拟的”。 因此，B组选出新大哥的坐标为：P哥（（1+3+8+9+10）/5，（2+1+8+10+7）/5）=（6.2，5.6）。 综合两组，新大哥为P1（0，0），P哥（6.2，5.6），而P2-P6重新成为小弟

4.再次计算小弟到大哥的距离：

round2

这时可以看到P2、P3离P1更近，P4、P5、P6离P哥更近，所以第二次站队的结果是：

• 组A：P1、P2、P3
• 组B：P4、P5、P6（虚拟大哥这时候消失）

5.第二届人民代表大会： 按照上一届大会的方法选出两个新的虚拟大哥：P哥1（1.33，1） P哥2（9，8.33），P1-P6都成为小弟

6.第三次计算小弟到大哥的距离：

round3

这时可以看到P1、P2、P3离P哥1更近，P4、P5、P6离P哥2更近，所以第二次站队的结果是：

• 组A：P1、P2、P3
• 组B：P4、P5、P6

我们发现，这次站队的结果和上次没有任何变化了，说明已经收敛，聚类结束，聚类结果和我们最开始设想的结果完全一致。

K-Means的细节问题：

1. K值怎么定？我怎么知道应该几类？ 答：这个真的没有确定的做法，分几类主要取决于个人的经验与感觉，通常的做法是多尝试几个K值，看分成几类的结果更好解释，更符合分析目的等。或者可以把各种K值算出的SSE做比较，取最小的SSE的K值。

2. 初始的K个质心怎么选？ 答：最常用的方法是随机选，初始质心的选取对最终聚类结果有影响，因此算法一定要多执行几次，哪个结果更reasonable，就用哪个结果。 当然也有一些优化的方法，第一种是选择彼此距离最远的点，具体来说就是先选第一个点，然后选离第一个点最远的当第二个点，然后选第三个点，第三个点到第一、第二两点的距离之和最小，以此类推。第二种是先根据其他聚类算法（如层次聚类）得到聚类结果，从结果中每个分类选一个点。

3. K-Means会不会陷入一直选质心的过程，永远停不下来？ 答：不会，有数学证明K-Means一定会收敛，大致思路是利用SSE的概念（也就是误差平方和），即每个点到自身所归属质心的距离的平方和，这个平方和是一个函数，然后能够证明这个函数是可以最终收敛的函数。

4. 判断每个点归属哪个质心的距离怎么算？ 答：这个问题必须不得不提一下数学了…… 第一种，欧几里德距离（欧几里德这位爷还是很厉害的，《几何原本》被称为古希腊数学的高峰，就是用5个公理推导出了整个平面几何的结论），这个距离就是平时我们理解的距离，如果是两个平面上的点，也就是（X1，Y1），和（X2，Y2），那这俩点距离是多少初中生都会，就是√( (x1-x2)^2+(y1-y2)2） ，如果是三维空间中呢？√( (x1-x2)^2+(y1-y2)2+(z1-z2)^2 ；推广到高维空间公式就以此类推。可以看出，欧几里德距离真的是数学加减乘除算出来的距离，因此这就是只能用于连续型变量的原因。 第二种，余弦相似度，余弦相似度用向量空间中两个向量夹角的余弦值作为衡量两个个体间差异的大小。相比距离度量，余弦相似度更加注重两个向量在方向上的差异，而非距离或长度上。下图表示余弦相似度的余弦是哪个角的余弦，A，B是三维空间中的两个向量，这两个点与三维空间原点连线形成的角，如果角度越小，说明这两个向量在方向上越接近，在聚类时就归成一类：
   

   看一个例子（也许不太恰当）：歌手大赛，三个评委给三个歌手打分，第一个评委的打分（10，8，9） 第二个评委的打分（4，3，2），第三个评委的打分（8，9，10） 如果采用余弦相似度来看每个评委的差异，虽然每个评委对同一个选手的评分不一样，但第一、第二两个评委对这四位歌手实力的排序是一样的，只是第二个评委对满分有更高的评判标准，说明第一、第二个评委对音乐的品味上是一致的。 因此，用余弦相似度来看，第一、第二个评委为一类人，第三个评委为另外一类。 如果采用欧氏距离， 第一和第三个评委的欧氏距离更近，就分成一类人了，但其实不太合理，因为他们对于四位选手的排名都是完全颠倒的。 总之，如果注重数值本身的差异，就应该用欧氏距离，如果注重的是上例中的这种的差异（我概括不出来到底是一种什么差异……），就要用余弦相似度来计算。 还有其他的一些计算距离的方法，但是都是欧氏距离和余弦相似度的衍生，简单罗列如下：明可夫斯基距离、切比雪夫距离、曼哈顿距离、马哈拉诺比斯距离、调整后的余弦相似度、Jaccard相似系数……

5. 还有一个重要的问题是，大家的单位要一致！ 比如X的单位是米，Y也是米，那么距离算出来的单位还是米，是有意义的 但是如果X是米，Y是吨，用距离公式计算就会出现“米的平方”加上“吨的平方”再开平方，最后算出的东西没有数学意义，这就有问题了。 还有，即使X和Y单位一致，但是如果数据中X整体都比较小，比如都是1到10之间的数，Y很大，比如都是1000以上的数，那么，在计算距离的时候Y起到的作用就比X大很多，X对于距离的影响几乎可以忽略，这也有问题。 因此，如果K-Means聚类中选择欧几里德距离计算距离，数据集又出现了上面所述的情况，就一定要进行数据的标准化（normalization），即将数据按比例缩放，使之落入一个小的特定区间。去除数据的单位限制，将其转化为无量纲的纯数值，便于不同单位或量级的指标能够进行计算和比较。 标准化方法最常用的有两种：

   • min-max标准化（离差标准化）：对原始数据进行线性变换，是结果落到【0，1】区间，转换方法为 X’=（X-min）/（max-min），其中max为样本数据最大值，min为样本数据最小值。
   • z-score标准化（标准差标准化）：处理后的数据符合标准正态分布（均值为0，方差为1），转换公式：X减去均值，再除以标准差

6. 每一轮迭代如何选出新的质心？ 答：各个维度的算术平均，比如（X1，Y1，Z1）、（X2，Y2，Z2）、（X3，Y3，Z3），那就新质心就是【（X1+X2+X3）/3，（Y1+Y2+Y3）/3，（Z1，Z2，Z3）/3】，这里要注意，新质心不一定是实际的一个数据点。

7. 关于离群值？ 答：离群值就是远离整体的，非常异常、非常特殊的数据点，在聚类之前应该将这些“极大”“极小”之类的离群数据都去掉，否则会对于聚类的结果有影响。但是，离群值往往自身就很有分析的价值，可以把离群值单独作为一类来分析。

8. 用SPSS作出的K-Means聚类结果，包含ANOVA（单因素方差分析)，是什么意思？ 答：答简单说就是判断用于聚类的变量是否对于聚类结果有贡献，方差分析检验结果越显著的变量，说明对聚类结果越有影响。对于不显著的变量，可以考虑从模型中剔除。

(3)算法过程

输入：训练数据集 $ D ={x{(1)},x{(2)},…,x^{(m)}},聚类簇数,聚类簇数 k $ ;
  过程：函数 kMeans(D,k,maxIter)kMeans(D,k,maxIter) .
  1：从 DD 中随机选择 kk 个样本作为初始“簇中心”向量： $ {\mu{(1)},\mu{(2)},…,\mu^{(k)}} $ :
  2：repeat
  3：  令 Ci=∅(1≤i≤k)Ci=∅(1≤i≤k)
  4：  for j=1,2,…,mj=1,2,…,m do
  5：    计算样本 x(j)x(j) 与各“簇中心”向量 μ(i)(1≤i≤k)μ(i)(1≤i≤k) 的欧式距离
  6：    根据距离最近的“簇中心”向量确定 x(j)x(j) 的簇标记： λj=argmini∈{1,2,…,k}djiλj=argmini∈{1,2,…,k}dji
  7：    将样本 x(j)x(j) 划入相应的簇： Cλj=Cλj⋃{x(j)}Cλj=Cλj⋃{x(j)} ;
  8：  end for
  9：  for i=1,2,…,ki=1,2,…,k do
  10：    计算新“簇中心”向量： (μ(i))′=1|Ci|∑x∈Cix(μ(i))′=1|Ci|∑x∈Cix ;
  11：    if (μ(i))′=μ(i)(μ(i))′=μ(i) then
  12：      将当前“簇中心”向量 μ(i)μ(i) 更新为 (μ(i))′(μ(i))′
  13：    else
  14：      保持当前均值向量不变
  15：    end if
  16：  end for
  17：  else
  18：until 当前“簇中心”向量均未更新
  输出：簇划分 C=C1,C2,…,CK

二、MatLab

1、基本操作

(1)控制台输出：

在命令的末尾添加分号将抑制输出，但仍会执行该命令，正如您在工作区中所看到的。当您输入命令而没有以分号结尾时，MATLAB 将会在命令提示符下显示结果。

当您在命令提示符下仅输入变量名称时，MATLAB 将会返回该变量的当前值。

(2)变量：

a、命名：

您可以将 MATLAB 变量命名为符合以下规则的任何名称：以字母开头，并且仅包含字母、数字和下划线 (_)。MATLAB 变量还区分大小写。

b、保存：

您可以使用 save 命令将工作区中的变量保存到称为 MAT 文件的 MATLAB 特定格式文件中。

要将工作区保存到名为 foo.mat 的 MAT 文件中，请使用命令：

>> save foo

c、加载：

在工作区中，您可以看到 clear 命令清空了所有变量。您可以使用 load 命令从 MAT 文件加载变量。

>> load foo

clear 函数清理工作区。clc 命令清理命令行窗口。

d、部分加载和保存：

如果您只想加载或保存部分变量，可以使用函数的两个输入。尝试从文件 myData.mat 中仅加载变量 m：

>> load myData m

然后尝试将变量 m 保存到名为 justm.mat 的新 MAT 文件中：

>> save justm m

(3)内置函数和常量：

用 pi 表示 π , abs（计算绝对值）和 eig（计算特征值）,使用 sqrt 函数计算的平方根。

在命令行窗口中仅显示前四个小数位,您可以使用 format 函数控制显示的精度。请试着输入 format long 并显示 x 的值。输入 format short 可切换回默认显示。

(4)数组：

a、标量：

单个称为标量的数值实际上是一个 1×1 数组，也即它包含 1 行 1 列。如：x=4

b、数组：

您可以使用方括号创建包含多个元素的数组。

x = [3 5]

当您用空格（或逗号）分隔数值时（如前面的任务中所示），MATLAB 会将这些数值组合为一个行向量，行向量是一个包含一行多列的数组 (1×n)。当您用分号分隔数值时，MATLAB 会创建一个列向量 (n×1)。

x = [1;3]

您可以组合使用空格和分号来创建一个矩阵，即包含多行多列的数组。输入矩阵时，您必须逐行输入它们。

x = [3 4 5;6 7 8]
x = 
    3    4    5
    6    7    8

在 MATLAB 中，您可以在方括号内执行计算。

x = [abs(-4) 4^2]
x = 
     4    16

c、等间距向量：

对于长向量，输入单个数值是不实际的。可用来创建等间距向量的替代便捷方法是使用 : 运算符并仅指定起始值和最终值。

y = 5:8
y = 
    5    6    7    8

请注意，当您使用冒号运算符时，不需要方括号。

: 运算符使用默认的间距 1，但是您可以指定您自己的间距，如下所示。

x = 20:2:26
x = 
    20    22    24    26

如果您知道向量中所需的元素数目（而不是每个元素之间的间距），则可以改用 linspace 函数：

linspace(first,last,number_of_elements)

注意，请使用逗号 (,) 分隔 linspace 函数的输入。

x = linspace(0,1,5)
x = 
    0    0.250    0.500    0.750    1.000

linspace 和 : 运算符都可创建行向量。但是，您可以使用转置运算符 (') 将行向量转换为列向量。

x = 1:3;
x = x'
x = 
    1
    2
    3

d、函数：

MATLAB 包含许多函数，可帮助您创建常用的矩阵，例如随机数矩阵。

x = rand(2)
x = 
    0.8147    0.1270
    0.9058    0.9134
请注意，`rand(2)` 命令中的 `2` 指定输出将为一个 2×2 的随机数矩阵。

x = rand(2,3)
x = 
    0.6324    0.2785    0.9575
    0.0975    0.5469    0.9649

使用 zeros 函数创建一个包含 6 行 3 列 (6×3) 的全零矩阵。将结果赋给名为 x 的变量

如何知道现有矩阵的大小？您可以使用 size 函数。

size(x)

您也可以使用一行代码创建与现有矩阵大小相同的矩阵。

rand(size(x))

e、数组索引：

*您可以使用行、列索引从数组中提取值。

y = A(5,7)

此语法将会提取 A 的第 5 行第 7 列的值，然后将结果赋给变量 y

您可以使用 MATLAB 关键字 end 作为行或列索引来引用最后一个元素。

y = A(end,2)

用作索引时，冒号运算符 (:) 可指代该维度中的所有元素。以下语法

x = A(2,:)

会创建一个包含 A 中第 2 行上所有元素的行向量。

单个索引值可用于引用向量元素。例如

x = v(3)

会返回向量 v 的第 3 个元素（当 v 为行向量或列向量时）。

索引可以是非连续数字。试着提取 density 的第一个、第三个和第六个元素。

p = density([1,3,6])

f、对向量执行数组运算：

MATLAB 的设计让您能够自然地处理数组。例如，您可以将一个标量值与数组中的所有元素相加。

y = x + 2

您可以将任意两个大小相同的数组相加。

z = x + y

您可以将数组中的所有元素与某个标量相乘或相除。

z = 2*x
y = x/3

MATLAB 中的基本统计函数可应用于某个向量以生成单个输出。可以使用 max 函数来确定向量的最大值。

xMax = max(x)

MATLAB 的函数可在单个命令中对整个向量或值数组执行数学运算。

xSqrt = sqrt(x)

* 运算符执行矩阵乘法。因此，如果您使用 * 将两个大小相同的向量相乘，则由于内部维度不一致，您将会收到一条错误消息。

z = [3 4] * [10 20]
错误使用  * 
用于矩阵乘法的维度不正确。 

而 .* 运算符执行按元素乘法，允许您将两个大小相同的数组的对应元素相乘。

z = [3 4] .* [10 20]
z = 
    30    80

g、获取函数的多个输出：

size 函数可以应用于数组，以生成包含数组大小的单个输出变量。

s = size(x)

size 函数可以应用于矩阵，以生成单个输出变量或两个输出变量。使用方括号 ([ ]) 获得多个输出。

[xrow,xcol] = size(x)

可以使用 max 函数确定向量的最大值及其对应的索引值。max 函数的第一个输出为输入向量的最大值。执行带两个输出的调用时，第二个输出为索引值。

[xMax,idx] = max(x)

如果只需函数的第二个输出，可以使用波浪号字符 (~) 忽略特定输出。例如，您可能只需要包含向量中最大值的索引：

density = data(:,2)
[~,ivMax] = max(v2)
densityMax = density(ivMax)

h、帮助与文档：

您也可以使用 doc 函数打开文档。尝试使用如下代码打开 randi 的文档：

doc randi

(5)绘制向量图：

可以使用 plot 函数在一张图上绘制两个相同长度的向量。

plot(x,y)

plot 函数接受一个附加参数。使用该参数，您可以通过在引号中包含不同符号的方式来指定与之对应的颜色、线型和标记样式。

plot(x,y,"r--o")

以上命令将会绘制一条红色 (r) 虚线 (--)，并使用圆圈 (o) 作为标记。您可以在线条设定的文档中了解有关可用符号的详细信息

请注意，每个绘图命令都创建了一个单独的绘图。要在一张图上先后绘制两条线，请使用 hold on 命令保留之前的绘图，然后添加另一条线。

启用保留状态时，将继续在同一坐标区上绘图。要恢复默认绘图行为，即其中每个绘图都有自己的坐标区，请输入 hold off。

当您单独绘制一个向量时，MATLAB 会使用向量值作为 y 轴数据，并将 x 轴数据的范围设置为从 1 到 n（向量中的元素数目）。使用以下命令绘制向量 v1。

plot(v1)

plot 函数接受可选的附加输入，这些输入由一个属性名称和一个关联的值组成。

plot(y,"LineWidth",5)

以上命令将绘制一条粗线。您可以在线条属性文档中了解更多可用属性的详细信息。

使用 plot 函数时，您可在绘图参数和线条设定符之后添加属性名称-属性值对组。

plot(x,y,"ro-","LineWidth",5)

可以使用绘图注释函数（例如 title）在绘图中添加标签。此类函数的输入是一个字符串。MATLAB 中的字符串是用双引号 (") 引起来的。

title("Plot Title")

使用 ylabel 函数添加标签 "Mass (g)"。

您可以使用 legend 函数为绘图添加图例。

legend("a","b","c")

(6)导入数据：

要提取表变量，可以使用圆点表示法：

data.VariableName

如果您正在使用表，您可能希望将相关数据放在一起。您可以将计算结果赋给表，而不是创建单独的变量。

data.HeightMeters = data.HeightYards*0.9144

如果变量 data.HeightMeters 不存在，MATLAB 将在表中创建名为 HeightMeters 的新变量。

(7)逻辑索引：

关系运算符（例如 >、<、== 和 ~=）执行两个值之间的比较。相等或不相等比较的结果为 1 (true) 或 0 (false)。

您可以使用关系运算符将某个向量或矩阵与单个标量值进行比较。结果是与原始数组相同大小的逻辑数组。

[5 10 15] > 12
ans = 
    0    0    1

您可以使用逻辑数组作为数组索引，在这种情况下，MATLAB 会提取索引为 true 的数组元素。以下示例将会提取 v1 中大于 6 的所有元素。

v = v1(v1 > 6)
v =
    6.6678
    9.0698

您也可以对两个不同向量使用逻辑索引。

v = sample(v1 > 6)
s =
    18
    23

您可以使用逻辑索引在数组中重新赋值。例如，如果您要将数组 x 中等于 999 的所有值都替换为值 1，请使用以下语法。

x(x==999) = 1

要查找小于 4 且大于 2 的值，请使用 &：

x = v1(v1<4 & v1>2)

要查找大于 6 或小于 2 的值，请使用 |：

x = v1(v1>6 | v1<2)

(8)if,for:

仅当条件为 true 时，才执行 if 代码块的主体。

x = rand
if x>0.5
	y=3
end

通常，您可能还希望在所设条件不成立时执行其他代码。为此，您可以使用 else 关键字，如下所示。

x = rand
if x > 0.5
    y = 3
else
    y = 4
end

elseif 关键字可在 if 后使用，以添加更多条件。您可以包括多个 elseif 代码块。

运行以下代码时，循环体将被执行三次，因为循环计数器 (c) 通过 1:3（1、2 和 3）进行计数。

for c=1:3
	disp(c)
end

代码 pause(0.2) 在 0.2 秒处停止循环，以便绘图进行更新。请尝试通过增大值 0.2 来增加动画时间。

该循环执行 7 次，因为 density 向量有七个元素。如果您要对未知长度的向量执行循环，可以改用 length 函数：

for idx = 1:length(density)

使用 loglog 函数（用法同 plot 函数），在每个坐标轴上使用对数刻度绘制数据。

loglog(x,y,"*--")

(9)总结：

a、基本语法

示例	说明
x = pi	使用等号 (=) 创建变量。 左侧 (x) 是变量的名称，其值为右侧 (pi) 的值。
y = sin(-5)	您可以使用括号提供函数的输入。

b、桌面管理

函数	示例	说明
save	save data.mat	将当前工作区保存到 MAT 文件中。
load	load data.mat	将 MAT 文件中的变量加载到工作区。
clear	clear	清除工作区中的所有变量。
clc	clc	清除命令行窗口中的所有文本。
format	format long	更改数值输出的显示方式。

c、数组类型

示例	说明
4	标量
[3 5]	行向量
[1;3]	列向量
[3 4 5;6 7 8]	矩阵

d、等间距向量

示例	说明
1:4	使用冒号 (:) 运算符，创建一个从 1 到 4，间距为 1 的向量。
1:0.5:4	创建一个从 1 到 4，间距为 0.5 的向量。
linspace(1,10,5)	创建一个包含 5 个元素的向量。这些值从 1 到 10 均匀间隔。

e、创建矩阵

示例	说明
rand(2)	创建一个 2 行 2 列的方阵。
zeros(2,3)	创建一个 2 行 3 列的矩形矩阵。

f、索引

示例	说明
A(end,2)	访问最后一行的第二列中的元素。
A(2,:)	访问第二行所有元素。
A(1:3,:)	访问前三行的所有列。
A(2) = 11	将数组中第二个元素的值更改为 11。

g、数组运算

示例	说明
[1 1; 1 1]*[2 2;2 2] ans = 4 4 4 4	执行矩阵乘法。
[1 1; 1 1].*[2 2;2 2] ans = 2 2 2 2	执行按元素乘法。

h、多个输出

示例	说明
[xrow,xcol] = size(x)	将 x 中的行数和列数保存为两个不同变量。
[xMax,idx] = max(x)	计算 x 的最大值及其对应的索引值。

i、文档

示例	说明
doc randi	打开 randi 函数的文档页。

j、绘图

示例	说明
plot(x,y,"ro-","LineWidth",5)	绘制一条红色 (r) 虚线 (--) 并使用圆圈 (o) 标记，线宽很大。
hold on	在现有绘图中新增一行。
hold off	为下一个绘图线条创建一个新坐标区。
title("My Title")	为绘图添加标签。

k、使用表

示例	说明
data.HeightYards	从表 data 中提取变量 HeightYards。
data.HeightMeters = data.HeightYards*0.9144	从现有数据中派生一个表变量。

l、逻辑运算

示例	说明
[5 10 15] > 12	将向量与值 12 进行比较。
v1(v1 > 6)	提取 v1 中大于 6 的所有元素。
x(x==999) = 1	用值 1 替换 x 中等于 999 的所有值。

m、编程

示例	说明
if x > 0.5 y = 3 else y = 4 end	如果 x 大于 0.5，则将 y 的值设置为 3。 否则，将 y 的值设置为 4。
for c = 1:3 disp(c) end	循环计数器 (c) 遍历 值 1:3（1、2 和 3）。 循环体显示 c 的每个值。

三、聚类

1、模拟

(1)DTW

import numpy as np

# We define two sequences x, y as numpy array
# where y is actually a sub-sequence from x
x = np.array([2, 0, 1, 1, 2, 4, 2, 1, 2, 0]).reshape(-1, 1)
y = np.array([1, 1, 2, 4, 2, 1, 2, 0]).reshape(-1, 1)

from dtw import dtw

euclidean_norm = lambda x, y: np.abs(x - y)

d, cost_matrix, acc_cost_matrix, path = dtw(x, y, dist=euclidean_norm)

print(d)
>>> 0.1111111111111111 # Only the cost for the insertions is kept

# You can also visualise the accumulated cost and the shortest path
import matplotlib.pyplot as plt

plt.imshow(acc_cost_matrix.T, origin='lower', cmap='gray', interpolation='nearest')
plt.plot(path[0], path[1], 'w')
plt.show()

(2)K-Means: demo1

import numpy as np
import pandas as pd
import random
import sys
import time
class KMeansClusterer:
    def __init__(self,ndarray,cluster_num):
        self.ndarray = ndarray
        self.cluster_num = cluster_num
        self.points=self.__pick_start_point(ndarray,cluster_num)
         
    def cluster(self):
        result = []
        for i in range(self.cluster_num):
            result.append([])
        for item in self.ndarray:
            distance_min = sys.maxsize
            index=-1
            for i in range(len(self.points)):                
                distance = self.__distance(item,self.points[i])
                if distance < distance_min:
                    distance_min = distance
                    index = i
            result[index] = result[index] + [item.tolist()]
        new_center=[]
        for item in result:
            new_center.append(self.__center(item).tolist())
        # 中心点未改变，说明达到稳态，结束递归
        if (self.points==new_center).all():
            return result
         
        self.points=np.array(new_center)
        return self.cluster()
             
    def __center(self,list):
        '''计算一组坐标的中心点
        '''
        # 计算每一列的平均值
        return np.array(list).mean(axis=0)
    def __distance(self,p1,p2):
        '''计算两点间距
        '''
        tmp=0
        for i in range(len(p1)):
            tmp += pow(p1[i]-p2[i],2)
        return pow(tmp,0.5)
    def __pick_start_point(self,ndarray,cluster_num):
        
        if cluster_num <0 or cluster_num > ndarray.shape[0]:
            raise Exception("簇数设置有误")
      
        # 随机点的下标
        indexes=random.sample(np.arange(0,ndarray.shape[0],step=1).tolist(),cluster_num)
        points=[]
        for index in indexes:
            points.append(ndarray[index].tolist())
        return np.array(points)

(3)K-Means:demo2

import numpy as np
from matplotlib import pyplot as plt


def euclidean_distance(vecA, vecB):
    '''计算vecA与vecB之间的欧式距离'''
    # return np.sqrt(np.sum(np.square(vecA - vecB)))
    return np.linalg.norm(vecA - vecB)


def random_centroids(data, k):
    ''' 随机创建k个中心点'''
    dim = np.shape(data)[1]  # 获取向量的维度
    centroids = np.mat(np.zeros((k, dim)))
    for j in range(dim):  # 随机生成每一维中最大值和最小值之间的随机数
        min_j = np.min(data[:, j])
        range_j = np.max(data[:, j]) - min_j
        centroids[:, j] = min_j * np.mat(np.ones((k, 1))) + np.random.rand(k, 1) * range_j
    return centroids


def KMeans(data, k, distance_func=euclidean_distance):
    '''根据k-means算法求解聚类的中心'''
    m = np.shape(data)[0]  # 获得行数m
    cluster_assment = np.mat(np.zeros((m, 2)))  # 初试化一个矩阵，用来记录簇索引和存储距离平方
    centroids = random_centroids(data, k)  # 生成初始化点
    cluster_changed = True  # 判断是否需要重新计算聚类中心
    while cluster_changed:
        cluster_changed = False
        for i in range(m):
            distance_min = np.inf  # 设置样本与聚类中心之间的最小的距离，初始值为正无穷
            index_min = -1  # 所属的类别
            for j in range(k):
                distance_ji = distance_func(centroids[j, :], data[i, :])
                if distance_ji < distance_min:
                    distance_min = distance_ji
                    index_min = j
            if cluster_assment[i, 0] != index_min:
                cluster_changed = True
                cluster_assment[i, :] = index_min, distance_min ** 2  # 存储距离平方
        for cent in range(k):  # 更新质心，将每个族中的点的均值作为质心
            pts_in_cluster = data[np.nonzero(cluster_assment[:, 0].A == cent)[0]]
            centroids[cent, :] = np.mean(pts_in_cluster, axis=0)
    return centroids, cluster_assment

def show_cluster(data, k, centroids, cluster_assment):
    num, dim = data.shape
    mark = ['or', 'ob', 'og', 'oy', 'oc', 'om']
    for i in range(num):
        mark_index = int(cluster_assment[i, 0])
        plt.plot(data[i, 0], data[i, 1], mark[mark_index])
    for i in range(k):
        plt.plot(centroids[i, 0], centroids[i, 1], 'o', markeredgecolor='k', markersize=16)
    plt.show()


if __name__ == "__main__":
    data = []
    f = open("sz.txt", 'r')
    for line in f:
        data.append([float(line.split(',')[0]), float(line.split(',')[1])])
    data = np.array(data)
    k = 4
    centroids = random_centroids(data, k)
    centroids, cluster_assment = KMeans(data, k)
    show_cluster(data, k, centroids, cluster_assment)

2、项目代码

(1)入口程序

clear;
clc;
P_train = [];
T_train = [];
P_test = [];
% D:\cnn-eventdata\event
 [name,path,ReadTxtFilterIndex] = uigetfile({'*.csv;*.txt','File(*.txt,*.csv)';'*.avi','AVIVideoFile(*.avi)';'*.*','AllFile(*.*)'},'ReadVideo',...
     'MultiSelect','on',...       %是否能够多选,'off'不支持多选， 'on'支持多选
     'D:\data-test'); %设置默认路径

if(path~=0)%防止取消打开文件时产生错误
    S=strsplit(name,'.');%后缀提取
    suffix=char(S(2));%打开的文件的后缀，字符串
    if(suffix=='txt')%说明当前打开的是txt文件
        namelist = dir([path,'\*.txt']);%存储该文件夹下的所有文件
    else%说明当前打开的是csv文件
        namelist = dir([path,'\*.csv']);%存储该文件夹下的所有文件
    end
    for i=1:length(namelist)%将所有灾害标准波形载入data，以列的形式存
        fileNameArr{i}=namelist(i).name;
        namecell = namelist(i).name(1);
        path1=[path,fileNameArr{i}];
        traindata=load(path1);
        for j=1:size(traindata,1)
            train(j)=traindata(j,2);
        end
        P_train(1:size(train',1),i)=train';%每次data将train存储到列中，即一列为一个波形 
    end
end
X=P_train;
X=X(1:20:end,:);
X=X'; 

[Idx] = k_means(X, 2);

(2)k_means.m

function [ output ] = k_means(data, k_value)
% 功能：实现K-means算法的聚类功能；
% 输入：    data, 为一个 矩阵 M×N， 表示样本集，其中M表示共有M个样本，　N表示每一个样本的维度；
%           k_value, 表示聚类的类别数目；
% 输出：    output, 是一个列向量 M×１，表示每一个样本属于的类别编号；
% 作者： 殷和义；
% 时间： 2017年10月14日
% 从样本中，随机选取K个样本作为初始的聚类中心；
data_num = size(data, 1);
temp = randperm(data_num, k_value)';     
center = data(temp, :);
%用于计数迭代次数：
iteration = 0;
while 1
    %获得样本集与聚类中心的距离；
    distance = euclidean_distance(data, center);
    %将距离矩阵的每一行从小到大排序， 获得相应的index值，其实我们只需要index的第一列的值；
    [~, index] = sort(distance, 2, 'ascend');
    %接下来形成新的聚类中心；
    center_new = zeros(k_value, size(data, 2));
    
    for i = 1:k_value
        data_for_one_class = data(index(:, 1) == i, :);
        center_new(i,:) = DBA1(data_for_one_class);
   % center_new(i,:) = mean(data_for_one_class, 1);    %因为初始的聚类中心为样本集中的元素，所以不会出现某类别的样本个数为0的情况；
    end
    %输出迭代次数，给眼睛一个反馈；
    iteration = iteration + 1;
    fprintf('进行迭代次数为：%d\n', iteration);
    % 如果这两次的聚类中心不变，则停止迭代，跳出循环；
    if all(center_new(:) == center(:))
        break;
    end
    center = center_new;
    if iteration == 30
        break;
    end
end
output = index(:, 1); 
end

(3)d_TW.m

function dist=d__TW(compare_to_this_object,unknow_object)
    format long e;
    m=length(compare_to_this_object);
    n=length(unknow_object);
    c = ones(m,n);

    for i = 1:m     %可以看出这里在算法中把a竖着
        for j = 1:n
            tmp= (compare_to_this_object(i)-unknow_object(j))^2;      %欧式距离   
            if j == 1&& i == 1
                c(i,j) = tmp;   %如果是c(1,1)，则不用包含累积距离，直接用欧氏距离
            elseif j>1
                c(i,j) = c(i,j-1) + tmp;    %其他的考虑累积距离
            end
            
            if  i>1     %第一行和其他行的情况不太一样，所以分开考虑
                if j==1     %而当i>1时，第一列的值只能是欧氏距离加上累计距离
                    c(i,j) = tmp + c(i-1,j);
                else         %排除了特殊情况之后，其他的根据算法计算，选出最小的累积距离+欧氏距离
                    test1 = [c(i,j-1),c(i-1,j-1),c(i-1,j)];      %因为min()的参数是矩阵，没法直接使用3个参数
                    c(i,j) = tmp + min(test1);
                end
            end
            
        end
    end
    dist=c(m,n);  %最小的距离
    
end

(4)DBA1.m

% /*******************************************************************************
%  * Copyright (C) 2013 Francois PETITJEAN, Ioannis PAPARRIZOS
%  * 
%  * This program is free software: you can redistribute it and/or modify
%  * it under the terms of the GNU General Public License as published by
%  * the Free Software Foundation, version 3 of the License.
%  * 
%  * This program is distributed in the hope that it will be useful,
%  * but WITHOUT ANY WARRANTY; without even the implied warranty of
%  * MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.  See the
%  * GNU General Public License for more details.well
%  * 
%  * You should have received a copy of the GNU General Public License
%  * along with this program.  If not, see .
% %  ******************************************************************************/ 
% sequences=rand(100,20);
% mean=DBA(sequences);
% plot(mean);
function average = DBA1(sequences)
	average=sequences(1,:);
	for i=1:1
		average=DBA_one_iteration(average,sequences);
	end
end


function average = DBA_one_iteration(averageS,sequences)

	tupleAssociation = cell (1, size(averageS,2));
	for t=1:size(averageS,2)
		tupleAssociation{t}=[];
	end

	costMatrix = [];
	pathMatrix = [];

	for k=1:size(sequences,1)
	    sequence = sequences(k,:);
	    costMatrix(1,1) = distanceTo(averageS(1),sequence(1));
	    pathMatrix(1,1) = -1;
	    for i=2:size(averageS,2)
		costMatrix(i,1) = costMatrix(i-1,1) + distanceTo(averageS(i),sequence(1));
		pathMatrix(i,1) = 2;
	    end
	    
	    for j=2:size(sequence,2)
		costMatrix(1,j) = costMatrix(1,j-1) + distanceTo(sequence(j),averageS(1));
		pathMatrix(1,j) = 1;
	    end
	    
	    for i=2:size(averageS,2)
		for j=2:size(sequence,2)
		    indiceRes = ArgMin3(costMatrix(i-1,j-1),costMatrix(i,j-1),costMatrix(i-1,j));
		    pathMatrix(i,j)=indiceRes;
		    
		    if indiceRes==0
			res = costMatrix(i-1,j-1);
		    elseif indiceRes==1
			res = costMatrix(i,j-1);
		    elseif indiceRes==2
			res = costMatrix(i-1,j);
		    end
		    
		    costMatrix(i,j) = res + distanceTo(averageS(i),sequence(j));
		    
		end
	    end
	    
	    i=size(averageS,2);
	    j=size(sequence,2);
	    
	    while(true)
		tupleAssociation{i}(end+1) = sequence(j);
		if pathMatrix(i,j)==0
		    i=i-1;
		    j=j-1;
		elseif pathMatrix(i,j)==1
		    j=j-1;
		elseif pathMatrix(i,j)==2
		    i=i-1;          
		else
		    break;
		end
	    end
	    
	end

	for t=1:size(averageS,2)
	   averageS(t) = mean(tupleAssociation{t});
	end
	   
	average = averageS;

end

function value = ArgMin3(a,b,c)

	if (a

(5)euclidean_distance.m

function [ output ] = euclidean_distance(data, center)
% 用于计算训练样本与聚类中心的的欧氏距离的平方；
% 其中  data为一个 矩阵 M×N， 表示样本集，其中M表示共有M个样本，　N表示每一个样本的维度；
%      centre 为一个矩阵 K×N，表示K个聚类中心，N表示样本的维度；
%      output 为一个矩阵，大小为M×K； 第ｘ行ｙ列表示第X个样本与第Y个聚类中心的距离；（每一行表示一个样本与K个聚类中心的距离）；
% 作者：殷和义；
% 时间：2017年10月14日；
data_num = size(data, 1);
center_num = size(center, 1);
output = zeros(data_num, center_num);
 for i = 1:data_num
    for j = 1:center_num
%     difference = data - repmat(center(i,:), data_num, 1);    %求样本集与第i个聚类中心的差；
%     sum_of_squares = sum(difference .* difference, 2);        %求平方， 并对每一行求和；
%     output(:, i) = sum_of_squares; 

      output(i,j)= d__TW(center(j,:),data(i,:));
    end
end
end

四、结果

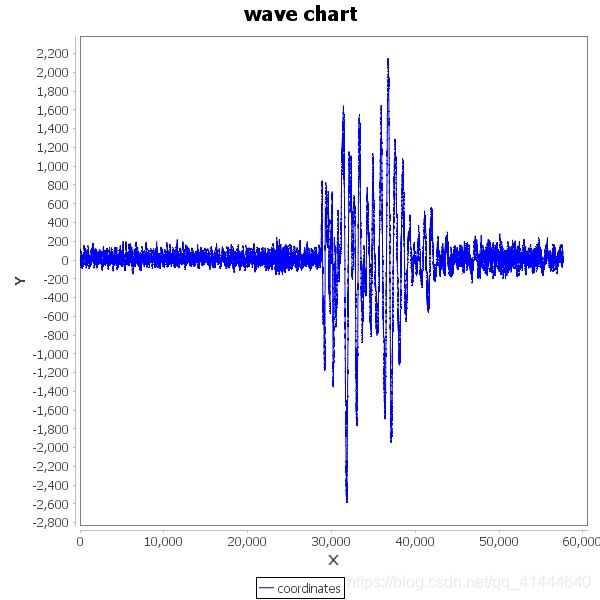
测试一：

取34个事件，41个噪声（数据存放于D:\data-test ，波形文件存放于D:\data-test-wave），聚类数目取2类，输入数据取Z通道数值

source	kind1	kind2	result
event1	1
event2	1
event3	1
event4	1
event5	1
event6		2
event7		2
event8		2
event9	1
event10	1
event11	1
event12		2
event13		2
event14		2
event15	1
event16	1
event17		2
event18		2
event19	1
event20		2
event21		2
event22		2
event23	1
event24	1
event25	1
event26	1
event27	1
event28		2
event29	1
event30	1
event31	1
event32	1
event33		2
event34		2
noise1	1
noise2	1
noise3	1
noise4	1
noise5	1
noise6	1
noise7	1
noise8	1
noise9	1
noise10	1
noise11	1
noise12	1
noise13	1
noise14	1
noise15	1
noise16	1
noise17	1
noise18	1
noise19	1
noise20	1
noise21	1
noise22	1
noise23	1
noise24	1
noise25	1
noise26	1
noise27	1
noise28	1
noise29	1
noise30	1
noise31	1
noise32	1
noise33	1
noise34	1
noise35	1
noise36	1
noise37	1
noise38	1
noise39	1
noise40	1
noise41	1

测试一result：

一类：

二类：

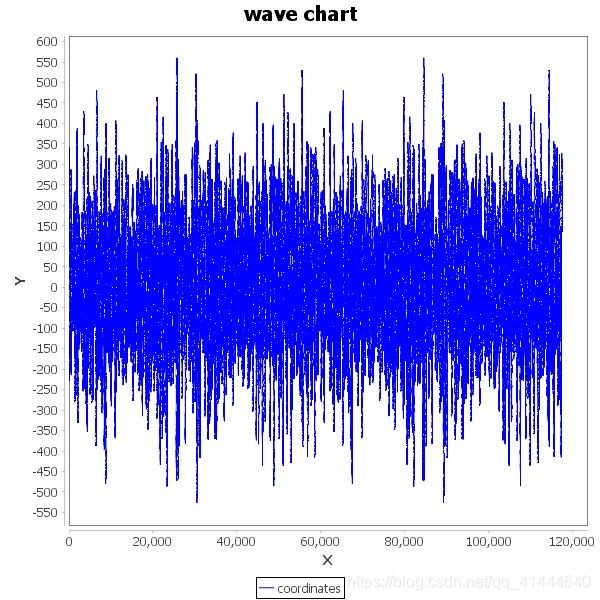
测试二：

取34个事件，41个噪声（数据存放于D:\data-test），聚类数目取3类，输入数据取Z通道数值

source	kind1	kind2	kind3	result
event1	1
event2	1
event3	1
event4	1
event5	1
event6			3
event7			3
event8			3
event9	1
event10		2
event11	1
event12			3
event13			3
event14			3
event15	1
event16	1
event17			3
event18			3
event19	1
event20			3
event21			3
event22			3
event23	1
event24	1
event25		2
event26	1
event27	1
event28			3
event29	1
event30	1
event31	1
event32	1
event33			3
event34			3
noise1		2
noise2		2
noise3		2
noise4		2
noise5	1
noise6		2
noise7		2
noise8		2
noise9		2
noise10		2
noise11		2
noise12	1
noise13		2
noise14		2
noise15		2
noise16		2
noise17		2
noise18		2
noise19		2
noise20		2
noise21		2
noise22		2
noise23		2
noise24		2
noise25		2
noise26		2
noise27		2
noise28		2
noise29		2
noise30		2
noise31		2
noise32		2
noise33		2
noise34		2
noise35		2
noise36		2
noise37		2
noise38		2
noise39		2
noise40		2
noise41		2

测试二result：

一类：

二类：

三类：

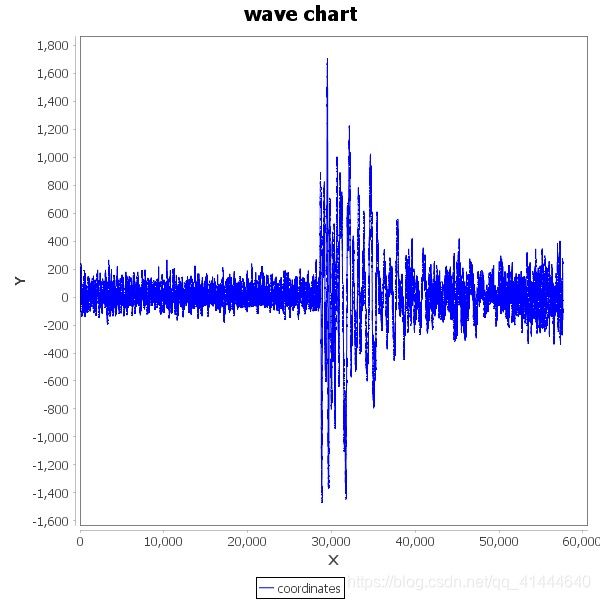
测试三：

取34个事件，41个噪声（数据存放于D:\data-test），聚类数目取4类，输入数据取Z通道数值

source	kind1	kind2	kind3	kind4	result
event1		2
event2		2
event3		2
event4		2
event5		2
event6				4
event7			3
event8				4
event9		2
event10	1
event11		2
event12			3
event13			3
event14			3
event15		2
event16		2
event17				4
event18			3
event19		2
event20				4
event21				4
event22			3
event23		2
event24		2
event25	1
event26		2
event27		2
event28			3
event29		2
event30		2
event31		2
event32		2
event33				4
event34			3
noise1	1
noise2	1
noise3	1
noise4	1
noise5		2
noise6	1
noise7	1
noise8	1
noise9	1
noise10	1
noise11	1
noise12		2
noise13	1
noise14	1
noise15	1
noise16	1
noise17	1
noise18	1
noise19	1
noise20	1
noise21	1
noise22	1
noise23	1
noise24	1
noise25	1
noise26	1
noise27	1
noise28	1
noise29	1
noise30	1
noise31	1
noise32	1
noise33	1
noise34	1
noise35	1
noise36	1
noise37	1
noise38	1
noise39	1
noise40	1
noise41	1

测试三result：

一类：

二类：

三类：

四类：