数据结构——B树

---

B树

可以用于查询的数据结构非常的多，比如说二插搜索树、平衡树、哈希表、位图、布隆过滤器，但如果需要存储一些数据量极大的数据，上述的数据结构就很不适用了，内存是不一定放的下的，比如用平衡树搜索一个贼大的文件。

因为数据量非常大，一次性无法加载到内存中，那么就可以在平衡树中保存数据项需要查找的部分，以及指向该数据在磁盘中的地址的指针。

虽然在上诉方法在内存中存放的是数据的地址，真实的数据是在磁盘上，解决了内存占用的问题。但是也有一定的缺陷：

• 当数据量比较大的时候，比如使用的是红黑树，虽然时间复杂度是$O(logn)$，但数据量比较大的时候，树的高度是比较高的。
• 当数据量特别大时，树中的节点可能无法一次性加载到内存中，这就需要增加磁盘的I/O次数

解决办法：就是减少I/O的次数，降低树的高度，引入多叉平衡树(B树)

1. 概念

B树是一棵M阶(M>2)的B树，是一棵平衡的M路平衡搜索树，可以是空树或者满足一下性
质：

1. 根节点至少有两个孩子
2. 每个非根节点至少有$M/2-1$(上取整)个关键字,至多有$M-1$个关键字，并且以升序排列
   例如：当M=3的时候，至少有3/2=1.5，向上取整等于2，2-1=1个关键字，最多是2个关键字
3. 每个非根节点至少有$M/2$(上取整)个孩子,至多有M个孩子
   例如：当M=3的时候，至少有3/2=1.5，向上取整等于2个孩子。最多有3个孩子。
4. key[i]和key[i+1]之间的孩子节点的值介于key[i]、key[i+1]之间
5. 所有的叶子节点都在同一层

2. B树插入分析

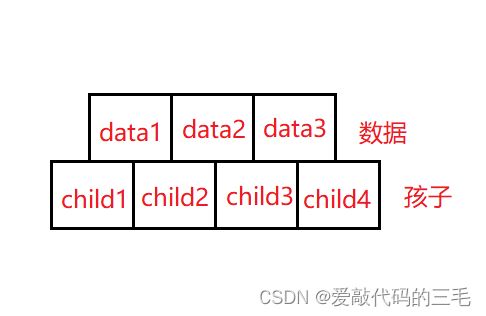
为了简单起见，假设M = 3. 即三叉树，每个节点中存储两个数据，两个数据可以将区间分割成三个部分，因此节点应该有三个孩子，为了后续实现简单期间，节点的结构如下：

注意：孩子永远比数据多一个。
插入过程当中，有可能需要分裂，分裂的
前提是：
假设，当前是要组成一个M路查找树，关键字数必须<=M-1**（这里关键字数**>M-1**就要进行节点拆分）**规则是：
把中间的元素，提取出来，放到父亲节点上，左边的单独构成一个节点，右边的单独构成一个节点。

假设用$53,139,75,49,145,36,101$构造B树的过程如下：

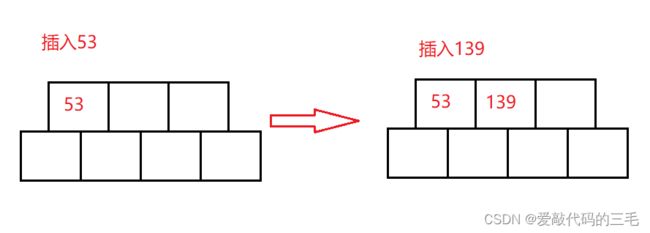
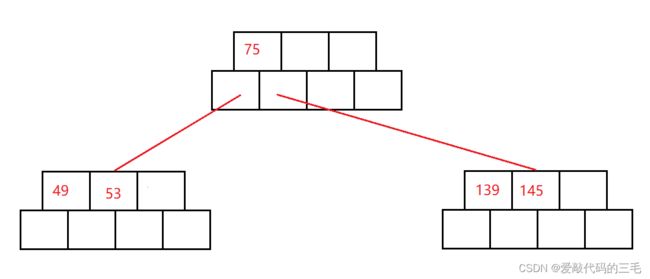
1. 先插入53和139

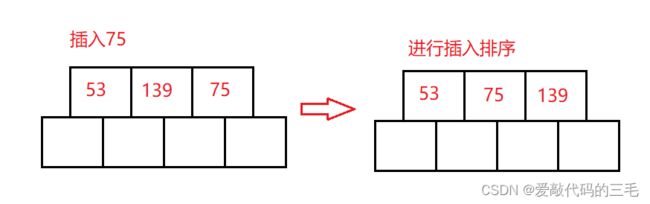
2. 再插入75，插入75后按照插入排序的思想对元素进行排序

   

3. 因为该节点的元素已经满了，就需要进行分裂

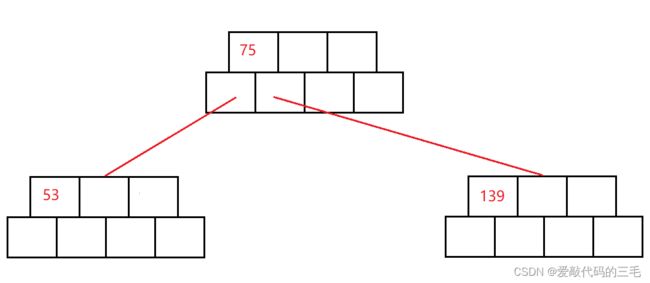
   节点分裂的步骤：

   • 找到节点数据域的中间位置
   • 给一个新节点，将中间位置的数据移动到新创建的节点中
   • 将中间位置的那个数据移动到父节点中
   • 将节点的关系连接好

   

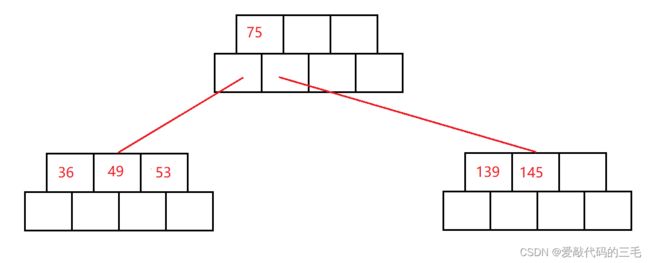
4. 插入49和145

   • 找到该元素的插入位置的位置
   • 按照插入排序的思想将节点插入到该节点的合适位置
   • 再检测是否满足B数的性质
   • 满足插入结束，不满足对节点进行分裂

   

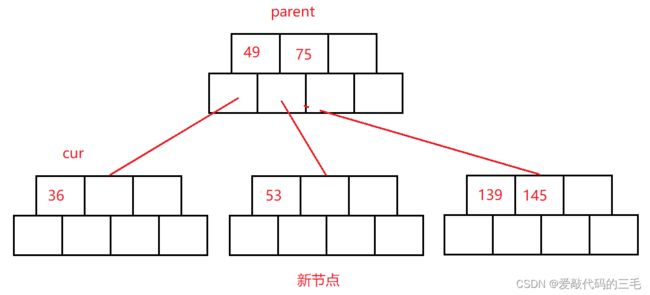
5. 插入36

   插入后违法了B树的性质，需要进行分裂

   

   对cur节点进行分裂：

   • 找到中间位置
   • 将中间位置右侧元素移动到新节点中
   • 将中间位置元素49移动到父节点parent中
   • 将新节点的父节点修改成parent

   

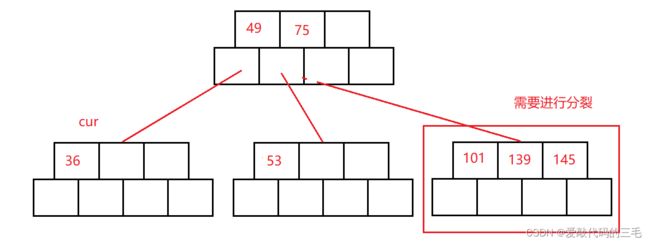
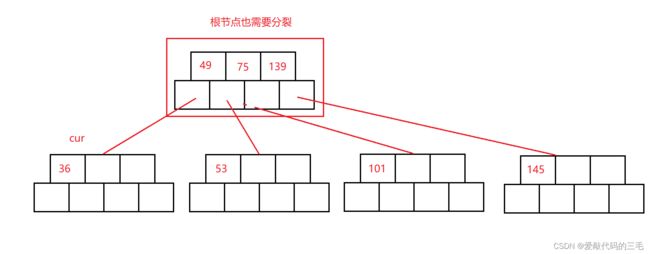
6. 插入数字101

   • 在B树中找到该节点的插入位置
   • 按照插入排序思想将该节点插入到指定位置
   • 检测插入后的节点元素个数是否小于M
   • 如果小于M插入完成，等于M则需要对该节点进行分裂

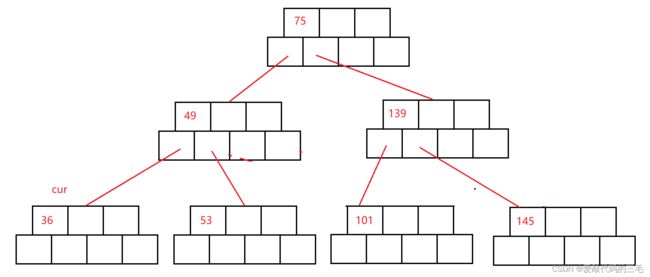
分裂完后，发现根节点也需要进行分裂，根节点分裂需要进行特殊处理，因为它会增加树的高度。

3.插入过程

1. 如果树为空，直接插入新节点中，该节点为树的根节点

2. 树非空，找待插入元素在树中的插入位置(注意：找到的插入节点位置一定在叶子节点中)

3. 检测是否找到插入位置(假设树中的key唯一，即该元素已经存在时则不插入)

4. 按照插入排序的思想将该元素插入到找到的节点中

5. 检测该节点是否满足B-树的性质：即该节点中的元素个数是否等于M，如果小于则满足

6. 如果插入后节点不满足B树的性质，需要对该节点进行分裂：

   • 申请新节点
   • 找到该节点的中间位置
   • 将该节点中间位置右侧的元素以及其孩子搬移到新节点中
   • 将中间位置元素以及新节点往该节点的双亲节点中插入，即继续4

7. 如果向上已经分裂到根节点的位置，插入结束

4. B树插入实现

B树的节点定义

// M叉树
private static final int M = 3;
static class BTreeNode {
    // 节点关键字
    int[] keys;
    // 孩子
    BTreeNode[] subs;
    // 关键字个数
    int keySize;
    // 父节点
    BTreeNode parent;

    public BTreeNode() {
        keys = new int[M];
        // 多给一个方便分裂
        subs = new BTreeNode[M+1];
    }
}
    

定义一个类方便查找指定节点

public class Pair<K,V> {
    K key;
    V val;

    public Pair(K key, V val) {
        this.key = key;
        this.val = val;
    }
}

插入代码

/**
 * B树
 */
public class BTree {
    // B树根节点
    BTreeNode root;

    public boolean insert(int key) {
        if (root == null) {
            root = new BTreeNode();
            root.keys[0] = key;
            root.keySize++;
            return true;
        }
        // 查找关键字是否已经存在
        Pair<BTreeNode,Integer> cur = find(key);
        if (cur.val != -1) {
            // 说明key已经存在，插入失败
            return false;
        }
        // 开始插入(插入排序)
        BTreeNode parent = cur.key;
        int i = 0;
        for (i = parent.keySize-1; i >= 0; i--) {
            if (parent.keys[i] >= key) {
                parent.keys[i+1] = parent.keys[i];
            } else {
                break;
            }
        }
        parent.keys[i+1] = key;
        parent.keySize++;

        // 判断是否需要分裂
        if (parent.keySize >= M) {
            split(parent);
        }
        return true;
    }

    /**
     * 对cur节点进行分裂
     * @param cur
     */
    private void split(BTreeNode cur) {
        BTreeNode newNode = new BTreeNode();
        BTreeNode parent= cur.parent;
        // 中间位置
        int mid = cur.keySize>>1;
        // 把mid往后的元素移动到新节点
        int j = 0;
        int i = mid+1;
        for (; i < cur.keySize; i++) {
            newNode.keys[j] = cur.keys[i];
            // 子节点引用
            newNode.subs[j] = cur.subs[i];
            // 修改子节点的parent引用
            if (newNode.subs[j] != null) {
                newNode.subs[j].parent = newNode;
            }
            newNode.keySize++;
            j++;
        }
        // 多拷贝一次最后的子节点
        newNode.subs[j] = cur.subs[i];
        if (newNode.subs[j] != null) {
            newNode.subs[j].parent = newNode;
        }
        //更新分裂节点关键字个数,-1指的是mid位置的节点要向上提
        cur.keySize = cur.keySize-mid-1;

        // 处理根节点分裂情况！
        if (cur == root) {
            root = new BTreeNode();
            root.keys[0] = cur.keys[mid];
            root.keySize++;
            root.subs[0] = cur;
            root.subs[1] = newNode;
            cur.parent = root;
            newNode.parent = root;
            return;
        }
        // 更新新节点的父亲节点
        newNode.parent = parent;

        // 将mid位置的元素向上提
        int midVal = cur.keys[mid];
        i = parent.keySize-1;
        for (; i >= 0; i--) {
            if (parent.keys[i] >= midVal) {
                parent.keys[i+1] = parent.keys[i];
                parent.subs[i+2] = parent.subs[i+1];
            } else {
                break;
            }
        }
        parent.keys[i+1] = midVal;
        parent.keySize++;
        // 将当前父节点的孩子节点设置为newNode
        parent.subs[i+2] = newNode;
        // 如果个数超过M递归分裂
        if (parent.keySize >= M) {
            split(parent);
        }
    }

    /**
     * 在B树中查找关键字是否已经存在
     * 找到返回节点和起下标，否则返回其父节点和-1
     * @param key
     * @return
     */
    private Pair<BTreeNode, Integer> find(int key) {
        BTreeNode cur = root;
        BTreeNode parent = root;
        int index = 0;
        while (cur != null) {
            while (index < cur.keySize) {
                if (cur.keys[index] == key) {
                    return new Pair<>(cur,index);
                } else if (cur.keys[index] < key) {
                    index++;
                } else {
                    break;
                }
            }
            parent = cur;
            // 向子节点找
            cur = cur.subs[index];
            index = 0;
        }
        return new Pair<>(parent,-1);
    }
}

5.B树验证

对B树进行中序遍历，只要打印出来的数据是有序说明插入正确

/**
     * 验证B树
     * @param root
     */
    private void inorder(BTreeNode root){
        if(root == null)
            return;
        for(int i = 0; i < root.keySize; ++i){
            inorder(root.subs[i]);
            System.out.println(root.keys[i]);
        }
        inorder(root.subs[root.keySize]);
    }

6. B树性能分析

对于一棵节点为N度的B树，查找和插入需要$lo{g}_{M-1}N$~$lo{g}_{M/2}N$次比较。对于度为M的B树，每一个节点的子节点个数为$M/2$~$(M-1)$之间，因此树的高度应该要在$lo{g}_{M-1}N$和$lo{g}_{M/2}N$之间，在定位到该节点后，再采用二分查找的方式可以很快的定位到该元素。

B树的效率是很高的对于$N=62\ast 1000000000$个节点，如果M为1024，则$lo{g}_{M/2}N<=4$，既在620亿个元素中，如果这棵树的度为1024，则需要小于4次即可定位到该节点，然后利用二分查找，可以快速定位到该元素，大大减少了读取磁盘的次数。

总结：

1. B树实际上是一棵M叉平衡树
2. 非根节点的关键字数量[M/2-1,M-1]，因为每次满了之后，会拷走一半
3. 非根节点的孩子数量[M/2,M]
4. 所有的叶子节点都在同一层，所以B树是天然平衡的
5. M越大效率越高，但M越大也会有空间浪费的问题，节点分裂会拷走一半就会存在空间浪费的问题

7.B+树&B*树

B+树是B树的变形，也是一种多路搜索树：

其定义基本与B树相同，除了：

2. B+树非叶子节点的子树指针与关键字个数相同，而B树的孩子数量比关键字多一个
3. B+树非叶子节点的子树指针指向的子树都属于它的右子树，也就是大于当前节点
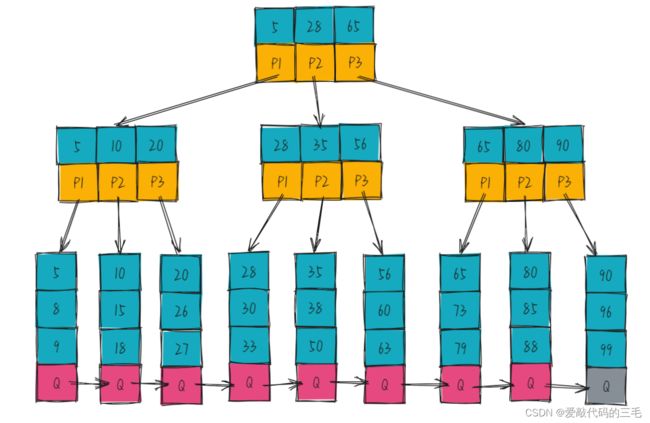
4. 为所有叶子节点增加一个链指针，也就是叶子节点是一个链表
5. B+数的叶子节点存储了数据，而非叶子节点只是存储了关键字。

对于B+树来说，如果要查找数据，那么一定得遍历整个树的高度，因为数据在叶子节点，但B树的每个节点都存储了数据，就不一定要遍历到叶子节点。

B+树的分裂:当一个结点满时，分配一个新的结点，
并将原结点中1/2的数据
复制到新结点，最后在父结点中增加新结点的指针，B+树的分裂只影响原结点和父
结点，而不会影响兄弟结点，所以它不需要指向兄弟的指针;

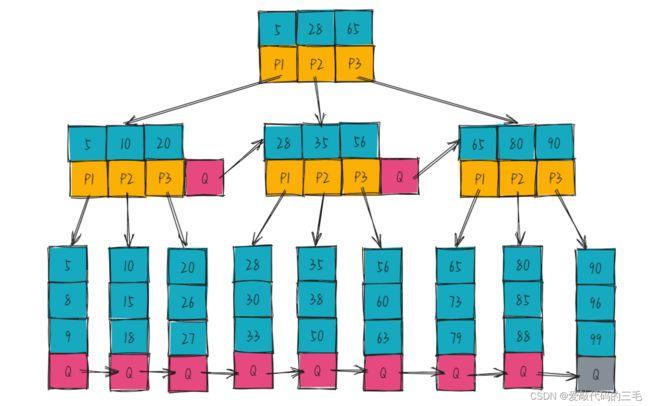
B*树

B*树是B+树的变形，在B+树的非根和非叶子节点再增加指向兄弟节点的指针。

B树的分裂:当一个结点满时，如果它的下一个兄弟结点未满，那么将一部分数据移到兄弟结点中，再在原结点插入关键字，最后修改父结点中兄弟结点的关键字(因为兄弟结点的关键字范围改变了)，如果兄弟也满了，则在原结点与兄弟结点之间增加新结点，并各复制1/3的数据到新结点，最后在父结点增加新结点的指针;所以，B*树分配新结点的概率比B+树要低，空间使用率更高;

8. 小结

• B树:多路搜索树，每个结点存储M/2到M个关键字，非叶子结点存储指向关键
  字范围的子结点;所有关键字在整颗树中出现，且只出现一次，非叶子结点可以命中;
• B+树:在B-树基础上，为叶子结点增加链表指针，所有关键字都在叶子结点中出现，非叶子结点作为叶子结点的索引，B+树总是到叶子结点才命中;
• B*树:在B+树基础上，为非叶子结点也增加链表指针，将结点的最低利用率从1/2提高到2/3;

9. B树的运用

B-树最常见的应用就是用来做索引。索引通俗的说就是为了方便用户快速找到所寻之物，比如：书籍目录可以让读
者快速找到相关信息，hao123网页导航网站，为了让用户能够快速的找到有价值的分类网站，本质上就是互联网
页面中的索引结构。
MySQL官方对索引的定义为：索引(index)是帮助MySQL高效获取数据的数据结构，简单来说：索引就是数据结
构。

注意：索引是基于表的，而不是基于数据库的。

MyISAM

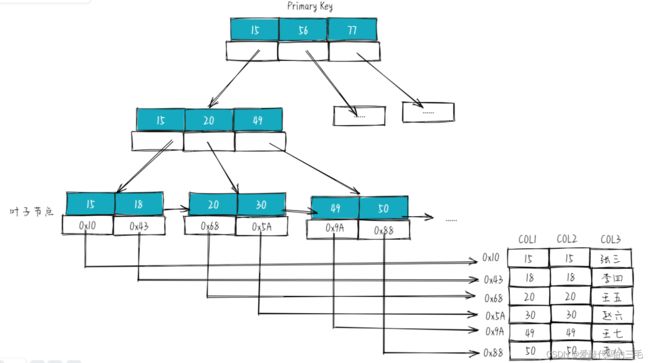
MyISAM引擎是MySQL5.5.8版本之前默认的存储引擎，不支持事物，支持全文检索，使用B+Tree作为索引结构，
叶节点的data域存放的是数据记录的地址，其结构如下：

上图是以以Col1为主键，MyISAM的示意图，可以看出MyISAM的索引文件仅仅保存数据记录的地址**。在MyISAM中，主索引和辅助索引（Secondary key）在结构上没有任何区别，只是主索引要求key是唯一的，而辅助索引的key**可以重复。如果想在Col2上建立一个辅助索引，则此索引的结构如下图所示 ：

同样也是一棵B+Tree，data域保存数据记录的地址。因此，MyISAM中索引检索的算法为首先按照B+Tree搜索算
法搜索索引，如果指定的Key存在，则取出其data域的值，然后以data域的值为地址，读取相应数据记录。
MyISAM的索引方式也叫做**“非聚集索引”**的

InnoDB

InnoDB存储引擎支持事务，其设计目标主要面向在线事务处理的应用，从MySQL数据库5.5.8版本开始，InnoDB存储引擎是默认的存储引擎。InnoDB支持B+树索引、全文索引、哈希索引。但InnoDB使用B+Tree作为索引结构
时，具体实现方式却与MyISAM截然不同。
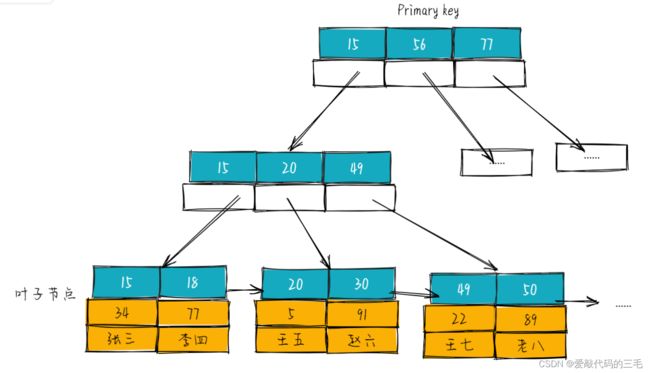
第一个区别是InnoDB的数据文件本身就是索引文件。MyISAM索引文件和数据文件是分离的，索引文件仅保存数据记录的地址。而InnoDB索引，表数据文件本身就是按B+Tree组织的一个索引结构，这棵树的叶节点data域保
存了完整的数据记录。这个索引的key是数据表的主键，因此InnoDB表数据文件本身就是主索引。

上图是InnoDB主索引（同时也是数据文件）的示意图，可以看到叶节点包含了完整的数据记录，这种索引叫做聚集索引。因为InnoDB的数据文件本身要按主键聚集，所以InnoDB要求表必须有主键（MyISAM可以没有），如果没有显式指定，则MySQL系统会自动选择一个可以唯一标识数据记录的列作为主键，如果不存在这种列，则MySQL自动为InnoDB表生成一个隐含字段作为主键，这个字段长度为6个字节，类型为长整形。
第二个区别是InnoDB的辅助索引data域存储相应记录主键的值而不是地址,所有辅助索引都引用主键作为data
域。

**聚集索引这种实现方式使得按主键的搜索十分高效，但是辅助索引搜索需要检索两遍索引：首先检索辅助索引获得主键，然后用主键到主索引中检索获得记录 **

10. 总结

1. 像链表，顺序表这样的是否可以?

   时间复杂度太高，不行

2. AVL树&红黑树是否可以?
   数据量大时树的高度较高，增加了I/O次数

3. 哈希表是否可以?
   哈希表存在哈希冲突哈希只能支持 是或者不是。比如: where id =? 或者 where id =? 做不到范围查找: where id >10

4. 为什么使用B+树，不适用B树?

   • 节点点不存储data，这样一个节点就可以存储更多的key。可以使得树更矮，所以I/O操作次数更少。
   • 叶子节点相连，更便于进行范围查找

聚簇索引和非聚簇索引的区别

• 聚簇索引将数据行存储在与索引相同的 B+ 树结构中，而非聚簇索引是将索引和主键 ID 存储在 B+ 树结构中；
• 数量限制不同：一张表只能有一个聚簇索引，但可以有多个非聚簇索引；
• 范围查询不同：聚簇索引中的数据行与索引行是一一对应的，因此聚簇索引通常比非聚簇索引更适合范围查询，而非聚簇索引需要进行两次查找：首先查找索引，然后查找数据行
• 非聚簇索引最大的缺点。 当查到索引对应的指针或主键后，可能还需要根据指针或主键再到数据文件或表中查询，首先检索辅助索引获得主键，然后用主键到主索引中检索获得记录
• 在Innodb下主键索引是聚集索引，在Myisam下主键索引是非聚集索引
• MyISAM 不提供事务支持。InnoDB 提供事务支持，实现了 SQL 标准定义了四个隔离级别。
• MyISAM 不支持外键，而 InnoDB 支持。

---