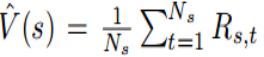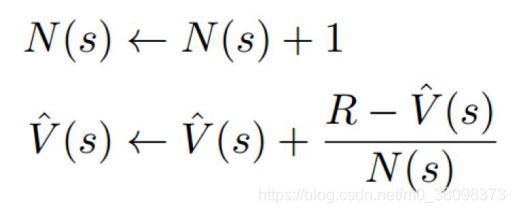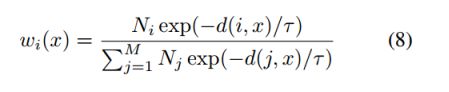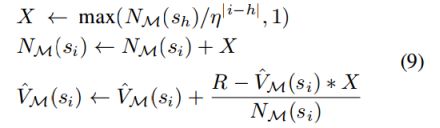AAAI18最佳论文:Memory-Augmented Monte Carlo Tree Search
本文为翻译AAAI18最佳论文:Memory-Augmented Monte Carlo Tree Search,如有错误,还望指正。转载请说明出处。
记忆增强的蒙特卡洛树搜索
摘 要
我们在本文中提出记忆增强的蒙特卡洛树搜索(Memory-Augmented Monte Carlo Tree Search,M-MCTS)并对其进行了评估,提供了利用在线实时搜索的泛化能力的新方法。M-MCTS 的核心思想是将 MCTS 结合一种记忆结构,其中每一项记录包含一个特定状态的信息。通过结合相似状态的估计,这些记忆被用于生成一个近似值估计。我们在本文中表明基于记忆的值逼近在温和条件下高概率地优于原始的蒙特卡洛评估方法。我们在围棋中评估了 M-MCTS。实验结果表明 M-MCTS 在相同的模拟次数下优于原始的 MCTS。
介绍
蒙特卡洛树搜索(MCTS)的核心思想是构建一个搜索树,且搜索树的状态由快速蒙特卡洛模拟(Coulom 2006)评估。若从给定博弈状态开始,并通过随机 Self-play 在观察到最终结果前模拟成千上万次博弈,然后我们就可以将模拟的平均输出作为状态值的估计。同时,MCTS 在模拟中会维护一个搜索树,因而借助它指导模拟的方向,其中我们可以使用老虎机算法(bandit algorithm)来权衡利用(exploitation)和探索(exploration)(Kocsis and Szepesvari 2006)。然而,MCTS 不能有效保证「大型状态空间」的价值估计准确度,因为在相对有限的搜索时间内,状态的平均值作为估计会有较高的方差。因此,不准确的估计会误导搜索树的构建,并严重降低程序的性能。
最近,已经有学者提出几种机器学习方法来克服 MCTS 的这种缺点。例如深度神经网络可以用来学习领域知识和逼近状态值的函数。这些方法和与 MCTS 相结合可以提供启发式的方法以提高搜索样本的效率(Silver et al. 2016; Tian and Zhu 2015)。
机器学习方法的成功可以很大程度上归因于模型的泛化性能,即类似的状态共享相似的信息。泛化空间的领域知识一般由函数近似表征,例如深度网络通过一般数据集或自生成的模拟数据集来离线训练(Silver et al. 2016)。
与从离线学习过程中探索泛化的研究相比,在线实时搜索并没有过多关注利用泛化的优势。本论文提出和评估了一种增强记忆的 MCTS 算法,它提供了一种利用在线泛化优势的替代型方法。我们设计了一种记忆,其中每个元素(entry)都包含特定状态的信息,并可作为构建在线值近似的基础。我们利用围棋的实验证明这种基于记忆的框架对于提升 MCTS 的性能十分有效,不论是在理论还是实践中。
预备知识
让S表示搜索问题中所有可能状态的集合。对于s属于S,
Rs,t表示状态s在模拟中的值估计,其中Rs,t是模拟的结果,Ns是从状态s开始到模拟结束的数量。V*(S): 是状态s的真实值。及以增强的蒙特卡洛树的主要思想就是:在一个记忆的帮助下,去接近变量的估计。每个元素都包含着特征的代表和一个特殊状态的模拟统计。近似估计如下进行:给定一个记忆![]() 和一个状态x,我们根据距离度量d(·,x)找到M个最相似的状态
和一个状态x,我们根据距离度量d(·,x)找到M个最相似的状态![]() x ⊂
x ⊂![]()
![]() ,并且计算一下基于记忆的变量估计值:
,并且计算一下基于记忆的变量估计值:
蒙特卡洛树搜索
MCTS 构建树以评估状态并进行快速模拟(Coulom 2006)。树中的每个节点对应一个具体的状态 s∈S,并包含模拟统计 V (s) hat 和 N(s)。在算法的每一次迭代中,一个模拟从一个初始状态 s_0 状态开始,之后进入两个阶段: in-tree 和 rollout。在当前的搜索树表征了状态 s_t 时,会应用树策略选择一个动作,以达到下一个状态。树策略的最常用选择是使用老虎机算法,例如 UCB1(Kocsis and Szepesvari 2006)。对于树之外的策略,树将应用 roll-out 策略模拟一场博弈直到结束,其中被访问的状态的轨迹为 T = {s_0, s_1, . . . , s_T },并在最后获得返回值 R。树中的 s∈T 的统计根据下式进行更新:
此外,树也同时在生长。在最简单的方案中,第一个被访问的尚未在树中的节点会被添加到树上。
记忆增强的蒙特卡洛树搜索
在前面的章节,我们提供了基于记忆的变量函数是由于平均值的函数,剩下的问题是设计一个算法可以融入到MCTS中。特别的是,首先要选择一个权重函数w =fτ(-c)的近似值。
Approximating w = fτ (−c)
Φ:生成一个状态特征表示的函数。有两个状态s,x∈ S,我们通过距离度量d(s, x)去近似于V∗ (s) and V∗ (x)之间的差异。
我们通过两个步骤来创建φ。
首先,取一个深度卷积神经网络的内层输出并对其进行归一化。我们通过 ζ : S → R L,表示这个过程。在实际过程中,计算L将非常消耗时间。我们通过应用哈希函数来克服这个问题。并且特征表示是通过φ(s) = h(ζ(s))来计算的。哈希特性的一个很好的特性是它可以保持内部的无偏估计。我们有:
E[cos(φ(s), φ(x))] = cos(ζ(s), ζ(x))
δx是对应于采样误差的项,它与模拟数成反比:δx ∝ 1/Nx。(模拟的次数越多,误差越小)。结合公式(7)和实际上ey近似于y+1,我们可以得到我们的w.
通过应用这些近似值,我们的模型成为基于核方法的特例,例如核回归。这里的核函数定义为:
τ在这些基于核方法中起平滑因子的作用。我们的模型也类似于基于记忆的神经网络中使用的“注意力”方案。
记忆操作
我们的方法中去维护一个记忆![]() 。
。![]() 的每个元素都包含一个特定的状态s。它包含状态的特征表示φ(s),以及它的模拟统计Vˆ (s) 和 N(s)。这里有三种操作M:更新,加入和查找。
的每个元素都包含一个特定的状态s。它包含状态的特征表示φ(s),以及它的模拟统计Vˆ (s) 和 N(s)。这里有三种操作M:更新,加入和查找。
更新
如果在MCTS期间状态s的模拟统计数据已经更新,我们也更新存储器中相应的值 Vˆ (s)和N(s)。
加入
为了包含状态s,我们添加一个新的记忆项{φ(s),V(s),N(s)}。 如果s已经存储在记忆中,我们只更新相应元素处的 Vˆ (s)和N(s)。 如果达到记忆的最大个数,我们用最新的一个去替换掉最近最少查询(更新)的。
查询
查询操作计算一个给定状态x∈S的基于记忆的近似值。我们首先根据距离函数d(·,x)找到![]() 中的前M个相似状态。然后通过
中的前M个相似状态。然后通过
计算近似记忆值,其中根据等式(8)计算权重w。
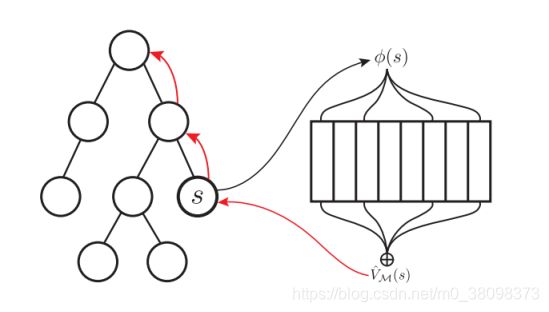
图 1:M-MCTS 的简要图示。当搜索到一个叶状态时,会生成一个特征表示φ(s),然后其被用于询问(query)基于记忆的值近似 VˆM(s)。VˆM(s)被用于根据下式更新状态s和状态s的所有过去状态,如图中的红色箭头所示。
寻找前M个相似状态这里有两个优点:首先,在一定范围内,限制了差异的最大值变量,在我们的分析中是有用的。第二点,在可扩展的非常大的记忆中进行查询。我们使用近似最近邻算法来执行基于SimHash的查询。(因为相关性越大,表示越相关)。
MCTS 结合记忆
我们现在介绍记忆增强 MCTS(M-MCTS)算法。图(1)提供了简要的图示。M-MCTS 和常规的 MCTS 的主要区别在于,M-MCTS 搜索树的每一个节点都会存储统计的一个扩展集合:
这里,NM 是近似记忆值VˆM(s)的估计次数。在 MCTS 的 in-tree 树搜索期间,我们使用(1 − λs)Vˆ (s) + λsVˆM(s) 取代 Vˆ (s)作为状态 s 的值,用于 in-tree 选择,例如在 UCB 公式中。λ_s 是一个延迟参数,确保不存在非对称的偏差。
在原始MCTS中,访问状态的轨迹T = {s0,s1,...。。。 ,sT}是在每次模拟结束时获得的。更新树中所有状态s∈T的统计变量。在M-MCTS中,我们也需要更新,通过更新操作。并且,当通过MCTS搜索到一个新的状态时,我们需要去计算它的φ(s),使用add(s)操作去使状态s在记忆中。获得 VˆM(s)和NM(s)最自然的方法是实时的计算和更新状态s的这些变量。但是,这种直接方法非常耗时,特别是当记忆尺寸较大时。相反,我们只计算叶节点的内存值,并将值传回给它的祖先。
具体来说,令sh∈T是刚刚添加到已经计算出特征表示φ(sh)的树中的状态,并且其查询(sh)计算其记忆近似值VM(sh)。
![]()
关于状态si ∈ {s0, . . . , sh},我们执行以下更新,η ≥ 1是一个衰减参数。
衰减参数η的原因是因为状态的记忆近似值更接近它的祖先。
相关工作
先前已经在游戏求解器中研究了利用类似状态信息的想法。(Kawano 1996)提供了一种技术,其中类似位置的证明被重新用于证明游戏树中的另一个节点。(Kishimoto and Muller 2004)将其应用于提供高效的图形历史交互解决方案,以解决问题跳棋和围棋的比赛。
记忆网络最近描述了神经网络和强化学习的记忆架构(Weston, Chopra, and Bordes 2015), 可微分神经计算机 (Graves et al. 2016), 匹配网络 (Vinyals et al. 2016)和神经连续控制(NEC) (Pritzel et al. 2017)。与我们的M-MCTS算法最相似的工作是NEC,它应用了一个记忆框架来提供强化学习中的动作值函数逼近。记忆架构和寻址方法与我们的相似。与他们的工作不同的是,我们提供了关于记忆如何影响价值估计的理论分析。此外,据我们所知,这项工作是第一个在MCTS中应用记忆架构的。
泛化的作用以前在转置表中被利用过(Childs, Brodeur, and Kocsis 2008), 时间差异搜索(TD search) (Silver, Sutton, and Muller 2012), 快速行动价值估计(RAVE) (Gelly and Silver 2011), and mNNUCT (Srinivasan et al. 2015)。
转置表提供了一种简单的通用形式。树中对应于相同状态的所有节点共享相同的模拟统计信息。通过将τ设置为接近零,我们的寻址方案可以非常类似于转置表。在τ> 0的M-MCTS中,记忆可以提供更多的推广,这在理论上和实践上都是有益的。
TD搜索使用线性函数来近似相关状态。在线实时搜索期间更新该线性函数。但是,对于复杂的非线性函数逼近(如神经网络),这种更新不可能在线执行。由于我们的基于记忆的方法是非参数化的,因此它提供了一种在实时搜索过程中进行泛化的替代方法。
RAVE使用基于直觉的全动作为第一种启发式,即动作的价值与被采取时无关。模拟结果不仅更新一个,而是更新模拟路径上的所有操作。mNN-UCT应用核回归来逼近一个状态值函数,该函数已经被证明与我们在第4节中使用我们的近似选择的寻址方案相似。然而,我们使用特征表示之间的差异作为距离度量,而mNN-UCT则应用树中节点之间的距离作为距离度量。而且,RAVE和mNN-UCT都没有提供任何理论上的理由。
实验
我们在中国古代的围棋游戏中评估M-MCTS。
实施细节
我们的实现应用了来自(Clark和Storkey 2015)的深度卷积神经网络(DCNN),该训练用于专业游戏记录的移动预测。它共有8层,包括一个卷积层64个7×7滤波器,两个卷积层64个5×5滤波器,两层48个5×5滤波器,两层32个5×5滤波器和一个全连接层。该网络对专业游戏记录的预测准确率约为44%。 首先从Conv7的输出中提取特征向量φ(s),Conv7是神经网络的最终完全连接层之前的最后一层。此输出的维度为23104。然后应用第4节中描述的使用特征哈希的降维步骤。特征哈希维度设置为4096,这给出φ(s)∈R 4096。
我们的SimHash实现中的哈希码有16位。 我们使用8个哈希表,每个哈希表对应一个独特的哈希函数。 我们也应用多重探测策略。 假设特征向量φ(s)被映射到第i个散列表的散列bin bi。 让bi的哈希码是hi。 为了在第i个表中搜索φ(s)的邻居,我们搜索哈希码的海明距离,在我们的实现中(海明距离)设置为1。 等式(9)衰减参数η更新记忆近似值时设置为2。
基线
我们在围棋游戏中评估了 M-MCTS,我们的基线结果是基于开源的围棋程序 Fuego(Enzenberger and Muller 2008 2017),但是添加了 DCNN 以提升性能。下图展示了实验结果:
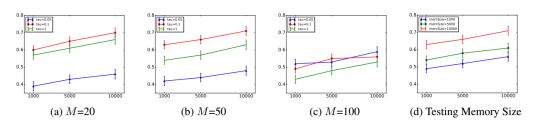
图 2:(a)-(c) 展示了测试 M 的不同值的结果。(d) 展示了测试不同记忆规模的结果。在所有的图中,x 轴是每次落子(s 到达下一个状态)的模拟数量,y 轴是与基线方法博弈的胜率。
我们采用(Gelly和Silver 2007)的方法,并使用DCNN来初始化模拟统计。 假设在刚添加到树上的状态s上调用DCNN。对于移动m,令pm为网络中的移动概率,并且s’通过取m来变换状态。 设pmax为网络输出移动概率的最大值。 我们计算两个统计量V DCNN(s’)= 0.5 *(1.0 + pm / pmax)和N DCNN(s)= CNN STRENGTH * pm / pmax。 这两个值在创建s’时用作初始统计。我们在实验中将CNN STRENGTH设置为200。
我们以同步方式在MCTS中实现DCNN,在DCNN评估返回后继续搜索。 为了提高速度,我们将DCNN呼叫限制在搜索期间访问的前100个节点。该基线与原始Fuego相比赢得了97%的胜率,每次移动10,000次模拟。 我们根据这个基线实施M-MCTS。 使用相同的DCNN来提取记忆的特征。
结果
我们首先研究参数M和τ如何影响M-MCTS的性能,因为这两个参数共同控制泛化程度。 参数M从{20,50,100}中选择,并且从{0.05,0.1,1}中选择τ。![]() 的大小设置为10000。
的大小设置为10000。
我们每次落子从 {1000, 5000, 10000} 使用不同的模拟次数,实验结果展示在上图 2(a)-(c) 中。在我们使用设定 {M = 50, τ = 0.1} 时获得了最好的结果,它以每次落子进行 10000 次模拟对抗基线算法并实现了 71% 的胜率。每个结果的标准误差约为2.5%。 对于M = 20和M = 50,M-MCTS的性能随着τ= 1和τ= 0.1的每次移动的模拟次数很好地扩展。 τ= 0.05根本无法击败基线。 我们相信原因在于,在这种情况下,M-MCTS只侧重于最近邻的泛化,但没有做足够的探索。 对于M = 100,M-MCTS在τ的任何设置中表现不佳,因为较大的M增加了包括较不相似状态的机会。
此外,我们也探索了不同记忆大小 {1000, 5000, 10000} 的影响。M 和 τ 分别设置为 50 和 0.1,实验结果在上图的 2(d) 中展示。直观上,我们会认为较大的记忆会有更好的性能,因为 query 会包含更多的候选状态,以上的实验结果也证明了这一点。M-MCTS通过|![]() | = 10000实现最佳性能,而小记忆|
| = 10000实现最佳性能,而小记忆|![]() | = 10000甚至可能对MCTS中的价值估计产生负面影响。我们还将M-MCTS与基线进行比较,计算时间相同。 通过设置M = 50,τ= 0.1并且每次移动5秒,M-MCTS相对于基线获得61%的胜率。
| = 10000甚至可能对MCTS中的价值估计产生负面影响。我们还将M-MCTS与基线进行比较,计算时间相同。 通过设置M = 50,τ= 0.1并且每次移动5秒,M-MCTS相对于基线获得61%的胜率。
结论和未来工作
在本论文中,我们提出了一个有效的方法来利用实时搜索的在线泛化。我们的方法,记忆增强的蒙特卡洛树搜索(M-MCTS),将原始的 MCTS 算法与记忆框架相结合,来提供基于记忆的在线数值近似。我们在理论和实践中证明这可以提高MCTS的性能。未来,我们计划探索以下两个方向。首先,我们想探索是否可以通过结合离线学习的数值近似来让我们的在线记忆框架获得更好的泛化性能;其次,让 M-MCTS 的特征表示重用一个神经网络来预测下一步。并且,我们计划探索将特征表示学习与M-MCTS以端到端方式相结合的方法,类似于(Pritzel et al。2017; Graves et al。2016)
(注)有三处推导过程未翻译