笔记 左程云算法基础
01 认识复杂度和简单排序算法
#时间复杂度
属于常数操作:int a = arr[i];数组中,只是算了一个偏移量;加减乘除;位运算...
不属于常数操作:int b = list.get(i);链表中,只能遍历去找
当两个算法时间复杂度相等时,只能实际去运行来确定哪个算法更优
#选择排序
每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到全部待排序的数据元素排完。
过程:看N眼,N次比较,1次swap;看N-1眼,N-1次比较,1次swap.......
看:N+N-1+N-2+... 比较:N+N-1+N-2+... swap:N次
=aN^2+bN+c
不要低阶项,只要高阶项,不要常系数==》O(n^2)
只需要开辟几个变量的额外空间==》O(1)
public static void selectionSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
for (int i = 0; i < arr.length - 1; i++) {//i~N-1
int minIndex = i;
for (int j = i + 1; j < arr.length; j++) {//i~N-1上找最小值下标
minIndex = arr[j] < arr[minIndex] ? j : minIndex;
}
swap(arr, i, minIndex);
}
}
public static void swap(int[] arr, int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}void swap(int arr[], int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
void selectionSort(int arr[],int len) {
if (arr[0] == NULL || len < 2) {
return;
}
for (int i = 0; i < len - 1; i++) {//确定范围为 i~N-1
int minIndex = i;
for (int j = i + 1; j < len; j++) {//i~N-1上找最小值下标
minIndex = arr[j] < arr[minIndex] ? j : minIndex;
}
swap(arr, i, minIndex);
}
}#冒泡排序
重复地走访过要排序的元素列,依次比较两个相邻的元素,如果顺序错误就把他们交换过来。走访元素的工作是重复地进行直到没有相邻元素需要交换,也就是说该元素列已经排序完成。
public static void bubbleSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
for (int e = arr.length - 1; e > 0; e--) {//规定范围 0~e
for (int i = 0; i < e; i++) {
if (arr[i] > arr[i + 1]) {
swap(arr, i, i + 1);
}
}
}
}
//交换arr的i和j位置上的值
public static void swap(int[] arr, int i, int j) {
arr[i] = arr[i] ^ arr[j];
arr[j] = arr[i] ^ arr[j];
arr[i] = arr[i] ^ arr[j];
}void swap(int arr[], int i, int j) {
arr[i] = arr[i] ^ arr[j];
arr[j] = arr[i] ^ arr[j];
arr[i] = arr[i] ^ arr[j];
}
void bubbleSort(int arr[],int len) {
if (arr == NULL || len < 2) {
return;
}
for (int e = len - 1; e > 0; e--) {
for (int i = 0; i < e; i++) {
if (arr[i] > arr[i + 1]) {
swap(arr, i, i + 1);
}
}
}
}#异或运算 ^
相同为0,不同为1:0^0=0 0^1=1 1^0=1 1^1=0
可以理解为无进位相加
- 0^N=0 N^N=0
- 满足交换律和结合律
//交换a和b的值(不用额外变量)
a=a^b;
b=a^b;
a=a^b;但是前提是:a和b的内存地址不同,地址相同时会被洗成0
题目-数组中找奇数次出现的数
1 在一个数组中,只有一个数出现了奇数次,其他数出现偶数次,怎么找出这个数?
int eor =0; 把eor从数组头异或到数组尾,结束时eor就是出现了奇数次的数(偶次彼此消掉了)
public static void printOddTimesNum1(int[] arr) {
int eor = 0;
for (int cur : arr) {
eor ^= cur;
}
System.out.println(eor);
}void printOddTimesNum1(int arr[],int len) {
int eor = 0;
for (int i = 0; i < len;i++) {
eor ^= arr[i];
}
cout<<"数组中次数为奇数的数为:"<异或运算的顺序无所谓的原因:因为异或运算可以看成无进位相加,结果中某一位的值只和所有数的这一位1出现的次数有关,和顺序无关
2 在一个数组中,两种数出现了奇数次,其他数出现偶数次,怎么找出这个数?
int eor =0;设出现奇数次数为a和b,把eor从数组头异或到数组尾,结束时eor就是a^b
所以eor=a^b (a!=b ——》eor!=0)
eor一定在某一位(至少一位)不等于0 ,假设第X位为1,说明a和b在第X位不一样
int eor'=0;把eor’从数组头异或到数组尾,只异或数组中那些X位不为0的数,结束时eor'就是a或者b
X位0的数不影响结果,只异或数组中那些X位不为0的数时,other2中1的个数为偶数次全消除,只剩a或b中一个,eor'只能碰到a或者b中一个,得到的结果就是另外一个
eor^eor'是a或b的另外一个
public static void printOddTimesNum2(int[] arr) {
int eor = 0;
for (int i=0;i//提取最右边的1
int rightOne = eor & (~eor + 1);
eor: 010100
~eor: 101011
~eor+1: 101100
eor&~eor+1: 000100void printOddTimesNum2(int arr[],int len) {
int eor = 0;
for (int i = 0; i < len; i++) {
eor ^= arr[i];
}
//eor=a^b
//eor!=0
//eor必然有一个位置是1
int rightOne = eor & (~eor + 1);//提取出最右边的1
int eorhasone = 0;//eor'
for (int i = 0; i < len; i++) {
if ((arr[i] & rightOne) != 0) {
eorhasone ^= arr[i];
}
}
int eor2 = eor ^ eorhasone;
cout << "数组中出现奇数次数为:" << eorhasone << "和" << eor2;
}#插入排序
对于少量元素的排序,它是一个有效的算法。插入排序是一种最简单的排序方法,它的基本思想是将一个记录插入到已经排好序的有序表中,从而一个新的、记录数增 1 的有序表 。在其实现过程使用双层循环,外层循环对除了第一个元素之外的所有元素,内层循环对当前元素前面有序表进行待插入位置查找,并进行移动。
插入排序的时间复杂度和数据状况有关
选择排序和冒泡排序和数据状况无关,不影响流程的进行
估计算法时间复杂度时,一律按照算法可能遇到的最差情况估计
public static void insertionSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
//0-0已经有序
//将0-i做到有序
for (int i = 1; i < arr.length; i++) { //0-i范围
for (int j = i - 1; j >= 0 && arr[j] > arr[j + 1]; j--) {
swap(arr, j, j + 1);
}
}
}
public static void swap(int[] arr, int i, int j) {
arr[i] = arr[i] ^ arr[j];
arr[j] = arr[i] ^ arr[j];
arr[i] = arr[i] ^ arr[j];
}void swap(int arr[], int i, int j) {
arr[i] = arr[i] ^ arr[j];
arr[j] = arr[i] ^ arr[j];
arr[i] = arr[i] ^ arr[j];
}
void insertionSort(int arr[],int len) {
if (arr == NULL || len < 2) {
return;
}
//0-0已经有序
//将0-i做到有序
for (int i = 1; i < len; i++) { //范围
for (int j = i - 1; j >= 0 && arr[j] > arr[j + 1]; j--) {
swap(arr, j, j + 1);
}
}
}#二分法
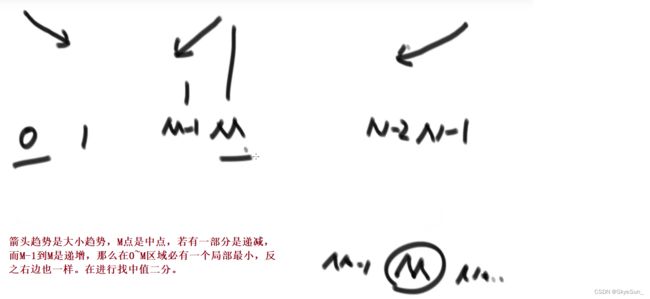
题目-局部最小问题
arr数组中,无序,任何两个相邻数一定不相等;找一个局部最小的位置,能否时间复杂度好于O(n)?(局部最小定义:位置为0的数<位置为1的数 或 N-2
二分不一定需要有序
优化一个流程,优化的方向:1.数据状况特殊 2.问题特殊
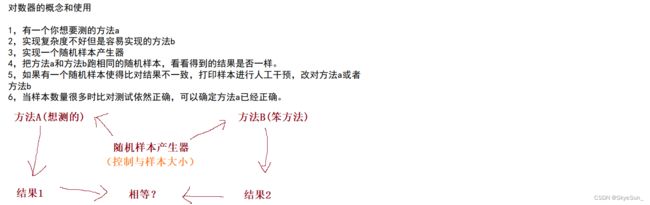
#对数器
// 和系统排序方法做对比
public static void comparator(int[] arr) {
Arrays.sort(arr);
}
//生成随机数组
public static int[] generateRandomArray(int maxSize, int maxValue) {
//Math.random() [0,1)所有小数,等概率返回一个
//Math.random()*N [0,N)所有小数,等概率返回一个
//(int)Math.random()*N [0,N-1]所有整数,等概率返回一个
int[] arr = new int[(int) ((maxSize + 1) * Math.random())];//长度随机
for (int i = 0; i < arr.length; i++) {
arr[i] = (int) ((maxValue + 1) * Math.random()) - (int) (maxValue * Math.random());//每个值随机
}
return arr;
}
// for test
public static int[] copyArray(int[] arr) {
if (arr == null) {
return null;
}
int[] res = new int[arr.length];
for (int i = 0; i < arr.length; i++) {
res[i] = arr[i];
}
return res;
}
// for test
public static boolean isEqual(int[] arr1, int[] arr2) {
if ((arr1 == null && arr2 != null) || (arr1 != null && arr2 == null)) {
return false;
}
if (arr1 == null && arr2 == null) {
return true;
}
if (arr1.length != arr2.length) {
return false;
}
for (int i = 0; i < arr1.length; i++) {
if (arr1[i] != arr2[i]) {
return false;
}
}
return true;
}
// for test
public static void printArray(int[] arr) {
if (arr == null) {
return;
}
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + " ");
}
System.out.println();
}
// for test
public static void main(String[] args) {
int testTime = 500000;
int maxSize = 100;
int maxValue = 100;
boolean succeed = true;
for (int i = 0; i < testTime; i++) {
int[] arr1 = generateRandomArray(maxSize, maxValue);//生成随机数组
int[] arr2 = copyArray(arr1);
bubbleSort(arr1);
comparator(arr2);
if (!isEqual(arr1, arr2)) {//判断两数组结果是否一样
succeed = false;
break;
}
}
System.out.println(succeed ? "Nice!" : "Wrong!");
int[] arr = generateRandomArray(maxSize, maxValue);
printArray(arr);
bubbleSort(arr);
printArray(arr);
}02 认识O(NlogN)的排序
#递归行为
题目-递归找数组上最大值
public static int getMax(int[] arr) {
return process(arr, 0, arr.length - 1);
}
public static int process(int[] arr, int L, int R) {
if (L == R) {//范围中只有一个数,直接返回
return arr[L];
}
int mid = L + ((R - L) >> 1);//找中点
int leftMax = process(arr, L, mid);//找左侧最大值
int rightMax = process(arr, mid + 1, R);//找右侧最大值
return Math.max(leftMax, rightMax);
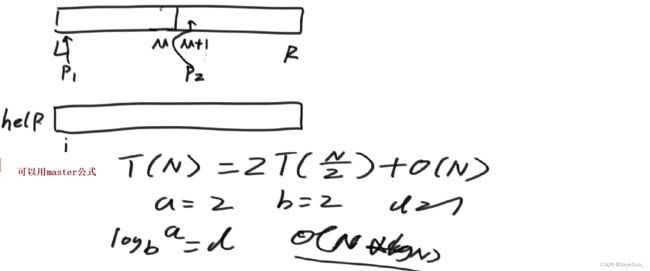
}master公式
#归并排序
将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
public static void mergeSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
mergeSort(arr, 0, arr.length - 1);
}
public static void mergeSort(int[] arr, int l, int r) {
if (l == r) {
return;
}
int mid = l + ((r - l) >> 1);
mergeSort(arr, l, mid);//左侧排序
mergeSort(arr, mid + 1, r);//右侧排序
merge(arr, l, mid, r);//两侧merge在一起
}
public static void merge(int[] arr, int l, int m, int r) {
int[] help = new int[r - l + 1];//辅助空间-数组等规模大小
int i = 0;
int p1 = l;
int p2 = m + 1;
while (p1 <= m && p2 <= r) {//两边都不越界时,比较拷贝++
help[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++];
}
while (p1 <= m) {//p2越界了(只会有一个while运行)
help[i++] = arr[p1++];
}
while (p2 <= r) {//p1越界了(只会有一个while运行)
help[i++] = arr[p2++];
}
for (i = 0; i < help.length; i++) {//依次拷贝回去
arr[l + i] = help[i];
}
}O(N^2)的排序每一轮的比较是独立的,一轮遍历中有大量的比较,但只解决一个数。
归并排序每一次的比较信息是往下传递的,变成了整体有序的部分继续去和其他部分merge,没有浪费比较行为。
题目-小和问题
暴力求解:对每个i的左边都遍历一遍,O(n^2)
深度改写mergesort的思路:
把问题变成——求右边有多少个数比i位置的数大,小和中就产生多少个i位置的数
此问题中merge时左右组数值相等时,一定要先拷贝右侧数组中的数并且不产生小和
public static int smallSum(int[] arr) {
if (arr == null || arr.length < 2) {
return 0;
}
return mergeSort(arr, 0, arr.length - 1);
}
public static int mergeSort(int[] arr, int l, int r) {//既要排好序,还要求小和
if (l == r) {
return 0;
}
int mid = l + ((r - l) >> 1);
return mergeSort(arr, l, mid) //左侧排序求小和的数量
+ mergeSort(arr, mid + 1, r) //右侧排序求小和的数量
+ merge(arr, l, mid, r);//两侧merge时求小和的数量
}
public static int merge(int[] arr, int l, int m, int r) {
int[] help = new int[r - l + 1];
int i = 0;
int p1 = l;
int p2 = m + 1;
int res = 0;
while (p1 <= m && p2 <= r) {
//左侧小于右侧时产生小和
res += arr[p1] < arr[p2] ? (r - p2 + 1) * arr[p1] : 0;
//左侧小于右侧时拷贝左侧,大于等于时拷贝右侧
help[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++];
}
while (p1 <= m) {
help[i++] = arr[p1++];
}
while (p2 <= r) {
help[i++] = arr[p2++];
}
for (i = 0; i < help.length; i++) {
arr[l + i] = help[i];
}
return res;
}
题目-逆序对问题
相当于求右边有多少个数比i位置的数小
题目-荷兰国旗问题
#快速排序
额外空间复杂度O(logN)
public static void quickSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
quickSort(arr, 0, arr.length - 1);
}
public static void quickSort(int[] arr, int l, int r) {
if (l < r) {
//等概率随机选一个数组中的数字把他放到数组最后面,和最右边的数做交换
swap(arr, l + (int) (Math.random() * (r - l + 1)), r);
//返回数组长度一定为2,是划分值等于区域的左边界和右边界
int[] p = partition(arr, l, r);
quickSort(arr, l, p[0] - 1);//<区
quickSort(arr, p[1] + 1, r);//>区
}
}
public static int[] partition(int[] arr, int l, int r) {
int less = l - 1;
int more = r;
while (l < more) {
if (arr[l] < arr[r]) {
swap(arr, ++less, l++);
} else if (arr[l] > arr[r]) {
swap(arr, --more, l);
} else {
l++;
}
}
swap(arr, more, r);
return new int[] { less + 1, more };
}
public static void swap(int[] arr, int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}#堆
堆(heap)通常是一个可以被看做一棵树的数组对象。堆总是满足下列性质:
- 堆中某个结点的值总是不大于或不小于其父结点的值;
- 堆总是一棵完全二叉树。
将根结点最大的堆叫做最大堆或大根堆,根结点最小的堆叫做最小堆或小根堆。
堆是非线性数据结构,相当于一维数组,有两个直接后继。
可以把数组从0出发的连续一段想象成完全二叉树:
| i位置左孩子 | 2*i+1 |
| i位置右孩子 | 2*i+2 |
| i位置父 | (i-1)/2 |
完全二叉树高度(logN)
//heapInsert 插入 O(logN)
//某个数现在在Index位置,继续往上移动
public static void heapInsert(int[] arr, int index) {
while (arr[index] > arr[(index - 1) / 2]) {//当前数大于父位置数
//while停止条件1.合适位置时 2.根节点index=0位置时(index - 1) / 2=0
swap(arr, index, (index - 1) /2);//交换
index = (index - 1)/2 ;//更新index位置
}
}//heapify 堆化 —— 变成一个大根堆 O(logN)
//从index位置开始,能否向下移动
public static void heapify(int[] arr, int index, int size) {
int left = index * 2 + 1;//左孩子下标
while (left < size) {//是否存在左孩子,越界不存在孩子
//右孩子存在并且右孩子>左孩子,右孩子胜出
//右孩子不存在或者左孩子>=右孩子,左孩子胜出
int largest = left + 1 < size && arr[left + 1] > arr[left] ? left + 1 : left;
//父亲和较大孩子之间,谁的值大,谁把下标给largest
largest = arr[largest] > arr[index] ? largest : index;
//父节点最大,不用往下走
if (largest == index) {
break;
}
//较大孩子和父交换
swap(arr, largest, index);
//index往下走
index = largest;
//新的左孩子
left = index * 2 + 1;
}
}没孩子了就停;有孩子但都没父节点大,就break
#堆排序
//堆排序 时间O(NlogN) 空间O(1)
堆排序的基本思想是:1、将带排序的序列构造成一个大顶堆,根据大顶堆的性质,当前堆的根节点(堆顶)就是序列中最大的元素;2、将堆顶元素和最后一个元素交换,然后将剩下的节点重新构造成一个大顶堆;3、重复步骤2,如此反复,从第一次构建大顶堆开始,每一次构建,我们都能获得一个序列的最大值,然后把它放到大顶堆的尾部。最后,就得到一个有序的序列了。
public static void heapSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
for (int i = 0; i < arr.length; i++) {
heapInsert(arr, i);
}
// 上述逻辑,建堆结束
// 元素交换,作用是去掉大顶堆
// 把大顶堆的根元素,放到数组的最后;换句话说,就是每一次的堆调整之后,都会有一个元素到达自己的最终位置
int size = arr.length;
swap(arr, 0, --size);
// 元素交换之后,毫无疑问,最后一个元素无需再考虑排序问题了。
// 接下来我们需要排序的,就是已经去掉了部分元素的堆了,这也是为什么此方法放在循环里的原因
while (size > 0) {
heapify(arr, 0, size);
swap(arr, 0, --size);
}
}//建堆优化
//一个个插入,插入时做heapInsert
for (int i = 0; i < arr.length; i++) { //O(N)
heapInsert(arr, i); //O(logN)
}
// 上述逻辑,建堆结束
//优化方法,直接把所有元素从最后一个从上到下做一遍heapify
//优化后复杂度为O(N)
for (int i=arr.length-1;i>=0;i--)
{
heapify(arr,i,arr.length);
}题目-堆排序扩展
- 建立由k个元素的小顶堆,然后取出顶上元素
- 堆顶用没有建堆的下一元素替代,重新建堆
- 反复调用,完成排序,此算法因为每个元素移动都在k以内,所以时间复杂度为O(NlogK)
public void sortedArrDistanceLessK(int[] arr, int k) {
//创建小根堆
PriorityQueue heap = new PriorityQueue<>();
//先把前k个数放入小根堆
int index = 0;
for (; index <= Math.min(arr.length, k); index++) {
heap.add(arr[index]);
}
int i = 0;
for (; index < arr.length; i++, index++) {
heap.add(arr[index]);//新加一个数放入小根堆
arr[i] = heap.poll();//弹出一个数放到i位置
}
//最后的一组直接一个个弹出就行了
while (!heap.isEmpty()) {
arr[i++] = heap.poll();
}
}
C++优先队列
c++ 优先队列(priority_queue) - 基础教程在线
大顶堆(降序)
//构造一个空的优先队列(此优先队列默认为大顶堆)
priority_queue big_heap;
//另一种构建大顶堆的方法
priority_queue,less > big_heap2; 小顶堆(升序)
//构造一个空的优先队列,此优先队列是一个小顶堆
priority_queue,greater > small_heap; 注意事项:如果使用less和greater,需要头文件:#include
比较器的使用
03 桶排序以及排序总结
#不基于比较的排序
不基于比较的排序,都一定要根据数据状况定制,应用范围窄。
计数排序
计数排序(Count Sort)是一个非基于比较的排序算法,它的优势在于在对一定范围内的整数排序时,它的复杂度为Ο(n+k)(其中k是整数的范围),快于任何比较排序算法。
计数排序的思想是在给定的一组序列中,先找出该序列中的最大值和最小值,从而确定需要开辟多大的辅助空间,每一个数在对应的辅助空间中都有唯一的下标。
找出序列中最大值和最小值,开辟Max-Min+1的辅助空间。最小的数对应下标为0的位置,遇到一个数就给对应下标处的值+1,。遍历一遍辅助空间,就可以得到有序的一组序列。
基数排序
- 确定数组中的最大元素有几位(MAX)(确定执行的轮数)
- 创建0~9个桶(桶的底层是队列),因为所有的数字元素都是由0~9的十个数字组成
- 依次判断每个元素的个位,十位至MAX位,存入对应的桶中,出队,存入原数组;直至MAX轮结束输出数组
//arr[begin...end]排序
public static void radixSort(int[] arr, int begin, int end, int digit) {
//基底
final int radix = 10;
int i = 0, j = 0;
//有多少个辅助洞见
int[] bucket = new int[end - begin + 1];
//有多少位就进出多少次桶
for (int d = 1; d <= digit; d++) {
//count数组处理完后 i位置的值x的含义:个位数<=i的数字有x个
int[] count = new int[radix];
//第d位数量统计
for (i = begin; i <= end; i++) {
j = getDigit(arr[i], d);
count[j]++;
}
//处理成前缀和
for (i = 1; i < radix; i++) {
count[i] = count[i] + count[i - 1];
}
//数组从右向左处理
for (i = end; i >= begin; i--) {
//拿出第d位数字
j = getDigit(arr[i], d);
//放入count[j]-1
bucket[count[j] - 1] = arr[i];
//单个词频--
count[j]--;
}
//复制回出桶的结果
for (i = begin, j = 0; i <= end; i++, j++) {
arr[i] = bucket[j];
}
}
}
public static int getDigit(int x, int d) {
return ((x / ((int) Math.pow(10, d - 1))) % 10);
}#稳定性
基础类型数据时稳定性没太大作用,非基础类型时可以保留相对次序。
稳定性:排序时值相同的元素在排序后能否保证其相对次序不变。
- 基于比较的排序,不能做到时间复杂度在O(NLogN)以下
- 时间在O(NlogN),不能做到空间在O(N)以下时还能稳定
- 在实际设计时,一般选择快排,因为其时间复杂度常数项较小,速度较快,考虑稳定性选择归并排序,有空间限制,选择堆排序。
常见的坑:
- 归并排序的额外空间复杂度可为O(1),但会因此丧失稳定性,“内部缓存法”,较难
- 原地归并排序可以使得空间复杂度为O(1),但会使得时间复杂度为O(N^2)
- 快排可以做到稳定性,但非常难
比较坑的题目:奇数放数组左边,偶数放在数组右边,且要求原有的相对次序不变。
答:这是一个0-1问题,快排无法达到,因为其进化过程做不到稳定性。
工程上对排序的改进:大样本,调度时一般选择快排,小样本时,选择插入排序。综合排序,利用各自的优势(时间快,空间低,以及稳定性的考虑)。
Java中的Array.sort()在基础类型时选择快排速度快不需要稳定性,非基础类型时选择归并排序保持稳定性。
04 链表
#哈希表
C++中通过 unordered_map 实现,增删改查的操作认为时间复杂度都是常数时间
存入为基础类型时,内部值传递,占用实际大小
存入不是基础类型时,按引用传递,占用内存地址的大小
《C++ Primer》读书笔记第十一章-2-关联容器操作_Real_JumpChen的博客-CSDN博客
c++ map与unordered_map区别及使用_别说话写代码的博客-CSDN博客_unordered_map和map的区别
C++ 哈希表_ZS_Wang_Blogs的博客-CSDN博客_c++ 哈希表
#有序表
#链表
题目-打印两个有序链表的公共部分
因为是有序链表,所以从两个链表的头开始进行如下判断:
如果head1的值小于head2 ,则head1 往下移动
如果head2的值小于head1 ,则head2 往下移动
如果head1和head2的值相等,则打印这个值,然后head1和head2都往下移动
head1和head2有任何一个移动到null,则整个过程停止
链表问题节省空间的方法:
1)额外数据结构记录(哈希表等)
2)快慢指针
题目-判断一个链表是否是回文结构
栈
把链表的全部内容依次放入栈中,再依次弹出栈中元素,并与链表依次进行比较,如果都相等,那么为回文结构,否则不是
时间复杂度:O(N)
空间复杂度:O(N)
快慢指针 + 栈
只把链表的右侧内容依次放入栈中,再依次弹出栈中元素,并与链表左侧依次进行比较,如果都相等,那么为回文结构,否则不是
通过快慢指针找到中点:
快指针一次走两步,慢指针一次走一步,当快指针走到结尾时,慢指针走到一半,然后把慢指针后面的部分,放到栈中
时间复杂度:O(N)
空间复杂度:O(N/2)
只用有限个指针
改变链表右侧区域,使整个右半区域反转,最后指向中间结点;利用指针分别从两端移动,每移动一次比较两值是否一样。返回true或false之前把链表恢复成原来的样子。
空间复杂度:O(1)
题目-将单向链表按某值划分成左边小、中间相等、右边大的形式
做法:利用辅助数组,放到数组中,然后利用荷兰国旗法排序
进阶做法:
- 将原链表中的所有节点依次分为三个链表,small,equal和big。
- 将三个链表重新串起来即可
- 整个过程需要注意对null节点的判断和处理。
题目-复制含有随机指针节点的链表
做法一:
- 采用一个Hash表,老结点的内存地址作为KEY值,从老结点中复制得来的新结点内存地址作为VALUE值,当结点遍历完毕后,所有的新旧结点均拷贝完毕
- 从头遍历老链表,每遍历一个结点,就得出他的rand和next指针,然后因为next指针和rand指针都是作为Hash表key存在,所以可以依据这个next和rand指针经由hash函数得出其对应新结点的所在地址(假设为N和R),再根据当前结点和哈希函数,得出当前结点的新结点,然后再设置新结点的next和rand指针分别指向N和R
- 重复步骤二,直到链表便利完毕
做法二:该思想主要运用新旧节点之间的位置关系省略了方法一中的额外的hash表空间
- 为每一个结点生成一个克隆结点,克隆结点只包含原结点的data值,将其作为对应老结点的下一个结点。比如对于链表 1 -> 2 -> 3 -> null,其中1的rand域指向3,2的rand域指向1;按照该规则,链表则变化为 1 -> 1’ -> 2 -> 2’ -> 3 -> 3’ -> null;
- 采用双指针pre和cur,pre始终指向cur的前一个结点,cur为当前遍历结点,当cur遍历到克隆节点时,比如1’,则pre指向该克隆节点的原结点,此时通过pre.rand.next即可得到cur结点(即1’)的rand指针指向的地址,随后cur跳到下一个旧结点(指2),如此直到遍历到链表空结点。
- 将新的链表进行撕裂,分成两个链表,一个全部由新结点组成,另一个全部由旧结点组成,然后返回全部由克隆节点组成的链表表头
public static Node copyListWithRand1(Node head) {
HashMap map = new HashMap();
Node cur = head;
while (cur != null) {
map.put(cur, new Node(cur.value));
cur = cur.next;
}
cur = head;
while (cur != null) {
map.get(cur).next = map.get(cur.next);
map.get(cur).rand = map.get(cur.rand);
cur = cur.next;
}
return map.get(head);
}
public static Node copyListWithRand2(Node head) {
if (head == null) {
return null;
}
Node cur = head;
Node next = null;
// copy node and link to every node
while (cur != null) {
next = cur.next;
cur.next = new Node(cur.value);
cur.next.next = next;
cur = next;
}
cur = head;
Node curCopy = null;
// set copy node rand
while (cur != null) {
next = cur.next.next;
curCopy = cur.next;
curCopy.rand = cur.rand != null ? cur.rand.next : null;
cur = next;
}
Node res = head.next;
cur = head;
// split
while (cur != null) {
next = cur.next.next;
curCopy = cur.next;
cur.next = next;
curCopy.next = next != null ? next.next : null;
cur = next;
}
return res;
} 判断一个链表是否有环
单链表只会有一条next指针。在有环的单链表上遍历的时候进了环就出不去了。
方法一:哈希表 unordered_set
遍历所有节点,每次遍历到一个节点时,判断该节点此前是否被访问过。
具体地,可以使用哈希表来存储所有已经访问过的节点。每次到达一个节点,如果该节点已经存在于哈希表中,则说明该链表是环形链表,否则就将该节点加入哈希表中。重复这一过程,直到遍历完整个链表即可。
方法二:快慢指针
让一个指针走的快一点,另外一个走的慢一点, 如果在移动的过程中,快指针反过来追上慢指针,就说明该链表为环形链表。否则快指针将到达链表尾部,该链表不为环形链表。
如果快慢指针相遇,相遇后快指针回到链表头部,慢指针停留在相遇处。之后两个指针都每次走一步,当两个指针再次相遇时就是第一个入环节点处。
题目-两个链表相交的一系列问题
1、判断链表是否有环
利用快慢指针,若链表有环,快慢指针一定会相交
快慢指针第一次相遇后,快指针回到头节点,变为一次走一步,两指针再次在入环节点处相遇
2、如果两个链表都无环
若相交,两链表必定是V或者Y型结构,从相交处到最后一定是公共部分。
判断相交:遍历第一个链表直到最后记为end1 长度length1 ,遍历第二个链表直到最后记为end2 长度length2,判断end1和end2内存地址是否一样,一样则相交。
找第一个相交的结点:设length1较大,则指针1从链表1的头部开始,先走length1-length2步;指针2从链表2头部开始,之后两个链表的指针一起走,会在第一个相交的地方相遇。
(如果一个有环,一个无环,不可能有相交的情况)
3、如果两个链表都有环
入环节点相同:先相交再共享环
入环节点不同:两个链表分别有一个入环节点
05 二叉树
#递归遍历二叉树
递归序:按照递归顺序遍历,每个节点会遍历3次。
先序:对于所有子树,都是先打印头节点,左子树上所有节点,右子树上所有节点
为递归序加工所得,即递归遍历时第一次来到该节点时打印,其余两次什么也不做。
中序:对所有子树,先打印左节点,头节点,右节点
为递归序加工所得,即递归遍历时第二次来到该节点时打印,其余两次什么也不做。
中序:对所有子树,先打印左节点,右节点,头节点
为递归序加工所得,即递归遍历时第三次来到该节点时打印,其余两次什么也不做。
#非递归遍历二叉树
任何递归都可以改成非递归。
先序:准备一个栈,先把根节点放入栈中,重复步骤:
1.从栈中弹出一个节点cur 2.打印(处理)cur 3.(如果有的话)先将右节点压入栈中,再将左节点压入,重复
//非递归先序遍历
public static void preOrderUnRecur(Node head){
if (head != null){
Stack stack = new Stack<>();
stack.push(head);
while (!stack.isEmpty()){
head = stack.pop();
System.out.println(head.value);
if (head.right != null){
stack.push(head.right);
}
if (head.left != null){
stack.push(head.left);
}
}
}
}
后序:准备一个放置栈,一个收集栈,先把根节点放入放置栈中,重复步骤:
1.从栈中弹出一个节点cur放入收集栈 2.先将左节点压入栈中,再将右节点压入,重复 3. 之后打印收集栈。
public static void posOrderUnRecur1(Node head){
if (head != null){
Stack stack1 = new Stack<>();//放入的栈
Stack stack2 = new Stack<>();//收集的栈
stack1.add(head);
while (!stack1.isEmpty()){
head =stack1.pop();
stack2.add(head);
if (head.left != null){
stack1.add(head.left);
}
if (head.right != null){
stack1.add(head.right);
}
}
while (!stack2.empty()){
System.out.print(stack2.pop().value + " ");
}
}
System.out.println();
}
中序:准备一个栈
将其每棵子树整棵树左边界进栈,无左边界时依次弹出节点的过程中打印,然后对弹出节点的右子树重复同样的操作
public static void inOrderUnRecur(Node head){
Stack stack1 = new Stack<>();
if (head != null){
while (!stack1.isEmpty() || head != null) {//只要左边界上的数不为null则全部放入栈中
if (head != null) {
stack1.add(head);
head = head.left;
}else {//否则就弹出,并去找右边再去找对应的右边界
head = stack1.pop();
System.out.print(head.value + " ");
head = head.right;
}
}
}
System.out.println();
}
题目-二叉树的宽度优先遍历
深度优先遍历即先序遍历
宽度优先遍历——队列
宽度优先遍历:准备一个队列,先把头节点放入,之后取出后,再把其左节点放进去,之后再把其右节点放进去,重复这个过程
public static void widthOrder(Node head){
Queue queue = new LinkedList<>();
if (head == null){
return;
}
queue.add(head);
while (!queue.isEmpty()){
Node cur = queue.poll();
System.out.println(cur.value);
if (cur.left != null){
queue.add(cur.left);
}
if (cur.right != null){
queue.add(cur.right);
}
}
#搜索二叉树
对于每一棵子树而言,其左树的节点都比它小,右树的节点都比它大,就叫搜索二叉树。
判断搜索二叉树思路:中序遍历一下,结果一定是升序(有降序肯定不是搜索二叉树)
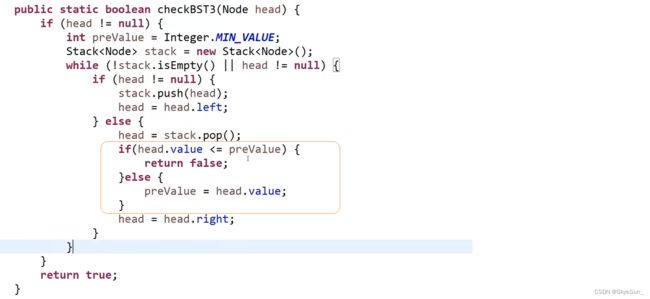
方法1.在中序遍历过程中,用一个全局变量用来记录上一次结点的值,看当前结点的值是否比上一次结点的值大,如果小于的话就不是搜索二叉树,大于的话就更新记录的值。
const int prevalue = MIN_VALUE
bool isBIT(ListNode* head)
{
if(head == NULL) return true;
bool isleftBST = isBST(head.left); //左树上检查是不是搜索二叉树
//如果左树不是搜索二叉树,那这棵树肯定不是搜索二叉树,返回false
if(!isleftBST) return false;
//左树是搜索二叉树,继续检查。
//看上一次处理到的节点,当前节点是否比我上次处理到的节点大
if(head->value < prevalue) return false;
else prevalue = head.value;//任何递归过程都能随意更改prevalue
//右树上查也是利用当前的prevalue判断
//最后判断右树,右树是BST,整棵树都是BST
return isBST(head->right);
}
方法2.基于非递归的方式
方法3.中序遍历的过程中,遇到一个结点就放入list里维持中序遍历的顺序,再遍历list看是不是升序的 (把中序遍历的打印时机变成处理时机)
public static boolean isBST(Node head) {
if (head == null) {
return true;
}
LinkedList inOrderList = new LinkedList<>();
process(head, inOrderList);
//中序遍历这个list,将得到的值放入inOrderList里面,用for循环看是不是升序
}
public static void process(Node node, LinkedList inOrderList) {
if (node == null) {
return;
}
process(node.left, inOrderList);
inOrderList.add(node);
process(node.right, inOrderList);
}
#完全二叉树
一个二叉树要么是满的,要不就是最后一层不满,就算不满也是从左到右依次变满的样子。
按宽度遍历
- 如果遇到的任何一个节点,有右孩子,没左孩子,直接返回false
- 在满足第一个条件的情况下,如果遇到第一个左右两个孩子不双全的情况,那么接下来遇到的所有节点都必须是叶节点,否则不是完全二叉树
public static boolean isCBT(Node head) {
if (head == null) {
return true;
}
LinkedList queue = new LinkedList<>();
//开关:表示事件是否发生。————用来记录是否遇到了左右两个孩子不双全的节点
boolean leaf = false;
Node l = null;
Node r = null;
queue.add(head);
while (!queue.isEmpty()) {
head = queue.poll();
l = head.left;
r = head.right;
//有右无左 或者 遇到了左右不双全并且此时结点又有孩子结点(不是叶子结点)
if ((leaf && (l != null || r != null)) || (l == null && r != null)) {
return false;
}
if (l != null) {
queue.add(l);
}
if (r != null) {
queue.add(r);
}
if(l==null ||r==null)
{
leaf = true;
}
}
return true;
} #满二叉树
判断是否是满二叉树:1.统计最大深度L 2.统计结点个数N 3.满足N=2^L-1
#平衡二叉树
(前面判断满二叉树,平衡二叉树,完全二叉树等二叉树的题都可以用以下套路来解)递归套路
二叉树递归套路:列出所有可能性
平衡二叉树:对于任何一颗子树来说,其左树的高度和右树的高度差都不超过1
#递归套路判断是不是平衡二叉树
(基于能向左树要某些信息,向右树要某些信息的情况下,怎么罗列可能性。只有一种可能性就是三种条件都满足,不然就不是balanceTree)1.左子树是平衡二叉树 2.右子树是平衡二叉树 3.左子树和右子树高度差不能超过1
信息结构体:
左树需要知道它是不是平衡的?以及它的高度。
右树需要知道它是不是平衡的?以及它的高度。
因为左树和右树都是两个要求,所以递归函数的返回值得返回两值——是否平衡,高度多少
public static boolean isBalanced(Node head) {
return process(head).isBalanced;
}
public static class ReturnType {
public boolean isBalanced;
public int height;
public ReturnType(boolean isB, int hei) {
isBalanced = isB;
height = hei;
}
}
public static ReturnType process(Node x) {
//basecase 空树
if (x == null) {
return new ReturnType(true, 0);
}
//获得左右信息
ReturnType leftData = process(x.left);
ReturnType rightData = process(x.right);
//加工出自己的信息
int height = Math.max(leftData.height, rightData.height);
boolean isBalanced = leftData.isBalanced && rightData.isBalanced
&& Math.abs(leftData.height - rightData.height) < 2;
//往上返回
return new ReturnType(isBalanced, height);
}#递归套路判断是不是搜索二叉树
在能向左树和右树要信息的情况下,列可能性:
左树必须是搜索二叉树,并且 左树max值 < x
右树必须是搜索二叉树, 并且 右树min值 > x
这四个条件都成立整棵树才是搜索二叉树
递归套路:对每一个节点的要求都是一样的,所以不管你是哪棵树,一律返回三个信息,即整棵树是不是搜索二叉树,整棵树的最小值和最大值
递归返回值:左树要求和右树要求,求全集
class Solution {
public:
bool helper(TreeNode* root, long long lower, long long upper) {
if (root == nullptr) {
return true;
}
if (root -> val <= lower || root -> val >= upper) {
return false;
}
return helper(root -> left, lower, root -> val) && helper(root -> right, root -> val, upper);
}
bool isValidBST(TreeNode* root) {
return helper(root, LONG_MIN, LONG_MAX);
}
};
题目-最低公共祖先节点
给定两个二叉树的节点node1和node2,找到他们的最低公共祖先节点
方法一
- 将二叉树每个节点的父节点找出来并使用hashmap保存
- 将node1节点到root节点的路线保存到一个hsahset中
- node2利用保存父节点的哈希表向上遍历,第一个遇到hashset中已有的节点,就是公共祖先节点
//需要改变的函数参数,接收时一定要记得加&引用符号!!要细心。整整查了一个小时才发现为啥一直不通过...
class Solution {
public:
void process(TreeNode* root, unordered_map &fatherMap)
{
if(root==NULL||(root->left==NULL&&root->right==NULL)) {return;}
if(root->left!=NULL){
fatherMap.emplace(root->left,root);
process(root->left,fatherMap);
}
if(root->right!=NULL){
fatherMap.emplace(root->right,root);
process(root->right,fatherMap);
}
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
unordered_map fatherMap;
fatherMap.emplace(root,root);
process(root,fatherMap);
unordered_set set1;
TreeNode* cur=p;
while(cur!=fatherMap[cur]){
set1.emplace(cur);
cur=fatherMap[cur];
}
set1.emplace(root);
cur=q;
while(cur!=fatherMap[cur]){
if(set1.count(cur)){
return cur;
}else{
cur=fatherMap[cur];
}
}
return root;
}
}; 方法二 妙妙秒!
可能情况:
1.node1是node2的最低公共祖先,或者node2是node1的最低公共祖先
2.node1和node2不是彼此公共祖先,需要往上汇聚才能得到
从根节点开始一层层向下遍历,遇到node1或node2或空就对应返回node1或node2或空;如果都没有就接着往下遍历,直到找到这几个,开始返回。
返回的时候左子树不为空就返回左子树,右子树不为空就返回右子树,都为空就返回空。如果一个子树中既没有node1也没有node2,返回一定是null。如果发现左右子树都不为空,就返回该节点。
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if(root==NULL || root== p || root==q){
return root;
}
TreeNode* leftReturn =lowestCommonAncestor(root->left,p,q);
TreeNode* rightReturn =lowestCommonAncestor(root->right,p,q);
if(leftReturn!=NULL && rightReturn!=NULL){
return root;
}
//左右两子树,并不都有返回值
//1.左右都为空,返回空
//2.只有一个为空,返回不空的
return leftReturn==NULL? rightReturn:leftReturn;
}
};
题目-在二叉树中找到一节点的后继节点
后继结点:中序遍历顺序中一个节点的下一个节点
1.X有右子树时,后继结点是右子树上的最左的结点
2.X无右子树时,后继结点是一直往上找遇到的第一个,是自己父节点的左子树的结点。找不到时,就是整棵树的最右节点情况,后继结点为空
class Solution {
public:
Node* inorderSuccessor(Node* node) {
if(node==NULL){
return node;
}
if(node->right!=NULL){//后继结点是右子树上的最左的结点
return getLeftMost(node->right);
}else{//无右子树
Node* parent =node->parent;
//当前节点是父节点的右孩子
while(node->parent!=NULL && parent->left!=node){
node=parent;
parent=node->parent;
}
return parent;
}
}
Node* getLeftMost(Node* node){
if(node==NULL){
return node;
}
while(node->left!=NULL){
node=node->left;
}
return node;
}
};二叉树的序列化和反序列化
就是内存里的一棵树如何变成字符串形式,又如何从字符串形式变成内存里的树
如何判断一颗二叉树是不是另一棵二叉树的子树?
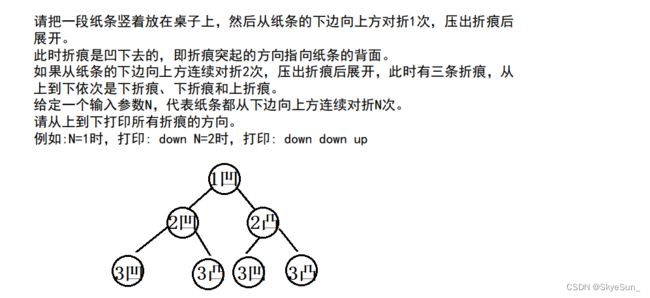
题目-折纸问题
可以看做是一棵头结点为凹折痕,每一棵左子树为凹右子树为凸的二叉树,打印中序遍历序列就是结果。
public class Code10_PaperFolding {
public static void printAllFolds(int N) {
printProcess(1, N, true);//1凹
}
// 递归过程,来到了某一个节点,
// i是结点的层数,N一共的层数,down == true 凹 down == false 凸
public static void printProcess(int i, int N, boolean down) {
if (i > N) {
return;
}
printProcess(i + 1, N, true);//i+1凹
System.out.println(down ? "凹 " : "凸 ");
printProcess(i + 1, N, false);//i+1凸
}
public static void main(String[] args) {
int N = 3;
printAllFolds(N);
}
}