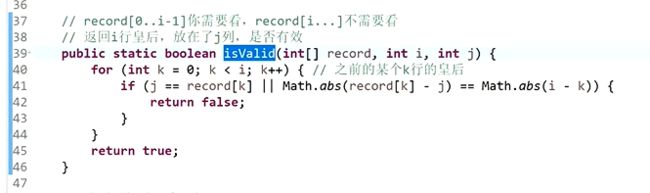
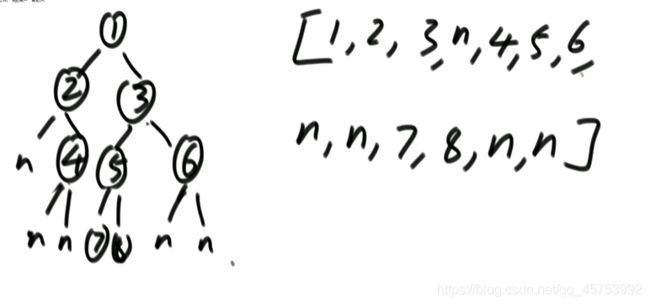左程云算法学习笔记

学习简介

2021寒假学习算法，在B站看到了左程云的算法，看了一下还不错。

认识复杂度，对数器，二分法与异或

你好！ 这是你第一次使用 Markdown编辑器 所展示的欢迎页。如果你想学习如何使用Markdown编辑器, 可以仔细阅读这篇文章，了解一下Markdown的基本语法知识。

线段树（区间修改树）

线段树定义：给定一个数组，使其实现以下在区间内的方法，且方法的时间复杂度都为O(logN)
线段树的创建：将长度为N的数组按二分法分下来，建立一颗二分树，将对应的二分区间存在一个新建的数组中，新建数组长度为4N，且0位置废弃

线段树代码：

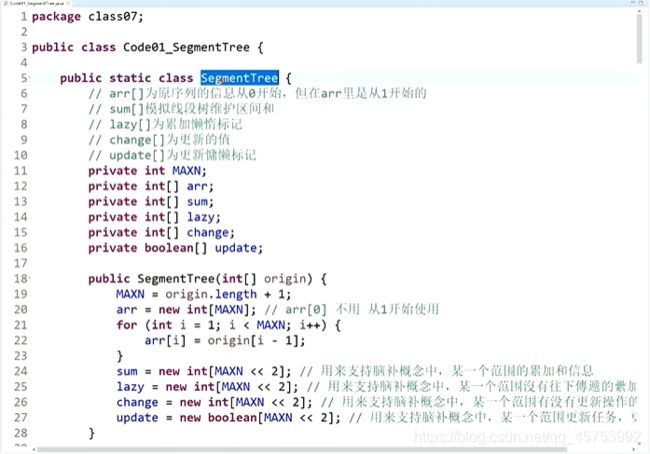
初始阶段，将sum数组中的值填好
l和r为区间的左右端点，rt为sum数组的下标即二分树的下标

layz更新：从上到下找，如果二分区间包含于想要加的数组，则停止继续向下，继续左右方向的寻找，直到找全为止，机制为能揽则揽，揽不住就下发给能揽的区间，懒任务躲不过了（也就是当前任务懒不住了），就会散发他懒的所有任务

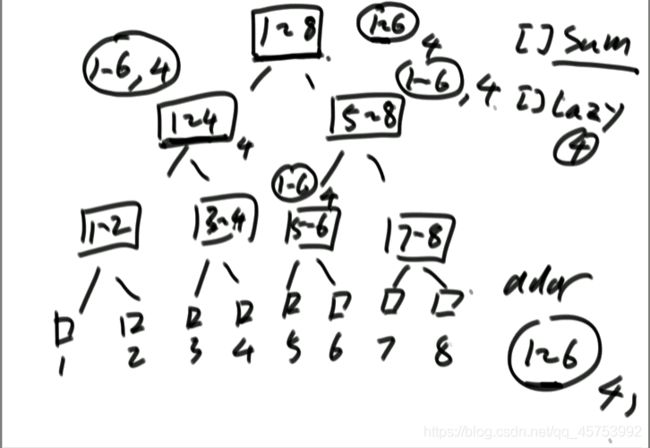
layz代码：



update：

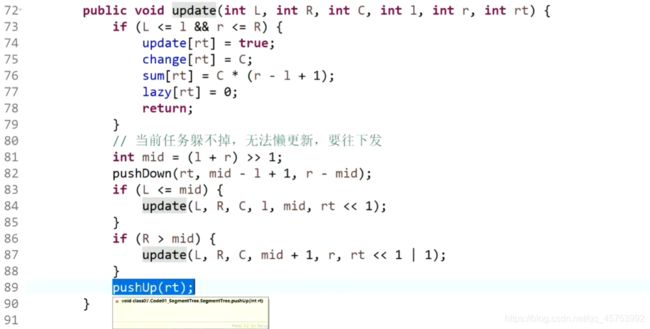
query：

感觉我需要用好长好长时间去理解了

比较器与堆

堆

定义：堆通常是一个可以被看做一棵完全二叉树的数组对象。堆又有其特性，分为大根堆（上面的下面的大）和小根堆（下面的上面的大）
有时候下标会从"1"开始，因为位运算比乘法快

创建大根堆代码：

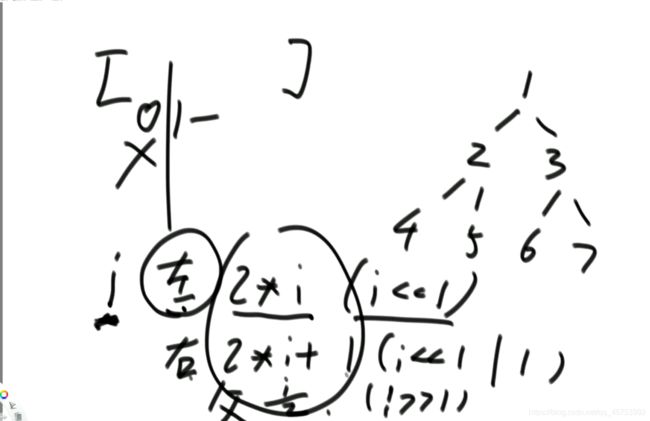
当有N个数时，树的高度为logN。

当你想删掉堆顶元素时：
heapify操作：
拿新堆顶与下层元素中的最大值比较，小了就交换，继续比较与交换

上述代码：


给一个无序的数组，使用堆来使它变得有序：

优化构建大根堆算法：时间复杂度为 O(N) 从下依次往上判断是否为大根堆，若否，则与它的较大的子结点交换


系统自带的堆：

看似优先队列，实则小根堆。

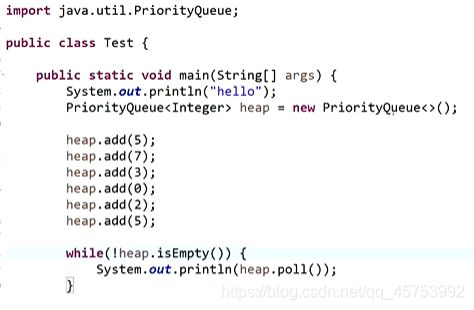
例题：

若k为5，则先让k+1个数构建小根堆，因为第0号位置只有可能是0-5上的数，然后弹出最小值，继续加上6号位置，继续上述操作

时间复杂度为O(N*logk)

比较器

代码

和python中的自定义排序函数类似，自己定义函数，定义比较规则


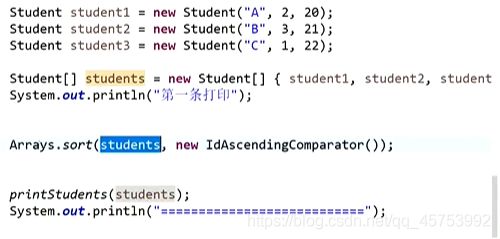
创建大根堆：
返回负数时o1放在上面

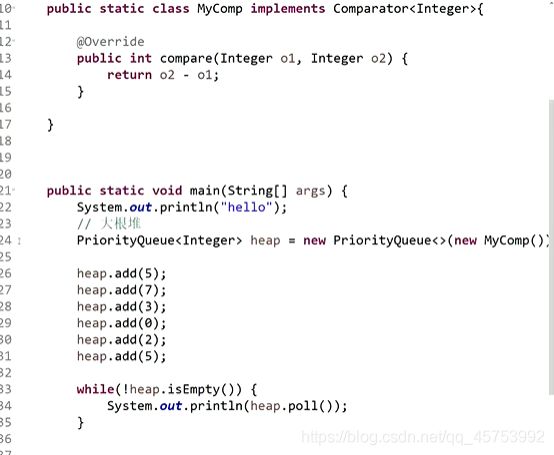
手动建堆：


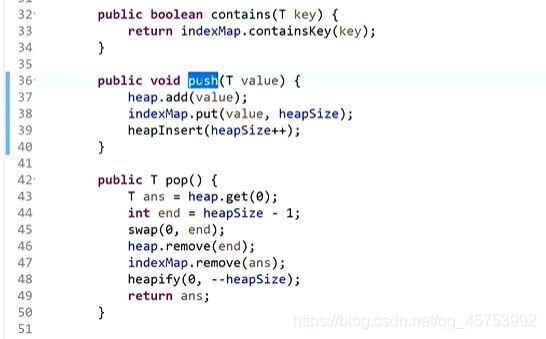
在修改值的时候，可能会上升也可能会下沉，所以heapInsert或者heapify只会中一个，所以都写，第一个没中出来看第二个

链表常见面试题

1、常用数据结构和技巧

2、快慢指针

4道题

都是慢指针走一步，快指针走两步，但是根据要求不同，细节处理方面也不同

（1）代码展示

（2）代码展示

（3）代码展示

（4）代码展示

2、

1、可以用栈来解决，遍历一个往栈里放一个，遍历完之后再弹出，或者先入栈再弹，遍历一个弹一个看是否一样。

代码展示：
第一种方法（用N个空间）：

第二种方法（用N/2个空间）：

使用快慢指针，找到中点，奇数个找中点，偶数个找中点的前一个，当快指针遍历完时，将满指针之后的元素入栈，再一一弹出与满指针前面的元素比较

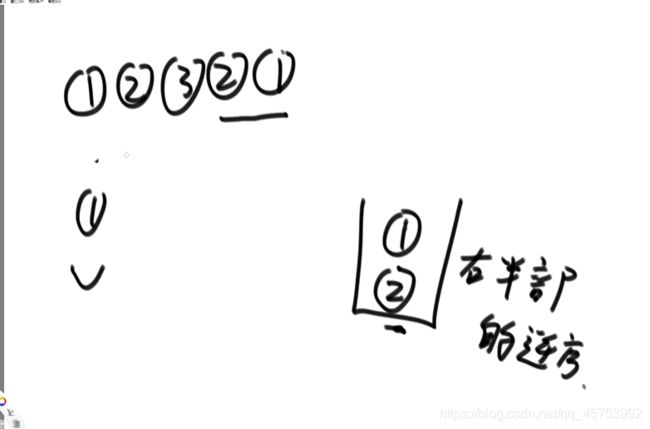
第三种方法（面试用）：使用快慢指针，当快指针走完时，将满指针到快指针逆序，然后两边同时向后移动比较


代码展示：


3、

题目解释：

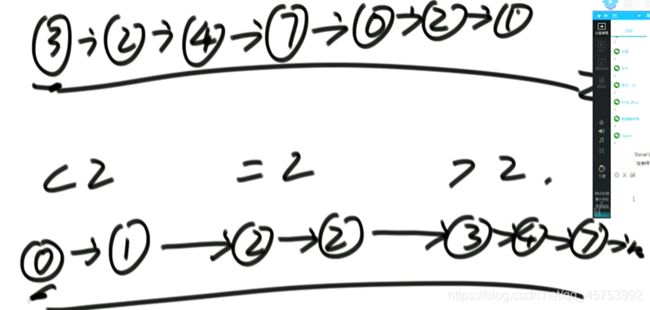
代码展示：
先将其存入数组中，对数组使用partition方法将其按传的值分割，最后再将其串起来

第三种方法（面试用）：

定义六个引用，sH和sT为小于传参的头指针和尾指针，eH和eT为等于传参的头指针和尾指针，bH和bT为大于传参的头指针和尾指针，遍历一个赋一个，最后再连起来，每一步操作都是O(1)，整体就是O(N)

代码展示：



4、

第一种方法：

先用哈希表（字典）存储节点，key为原节点，value为克隆节点，先看节点，通过1找到1’，然后通过1.next找到1’next,通过1.rand找到1’.rand，以此类推，最后返回头节点

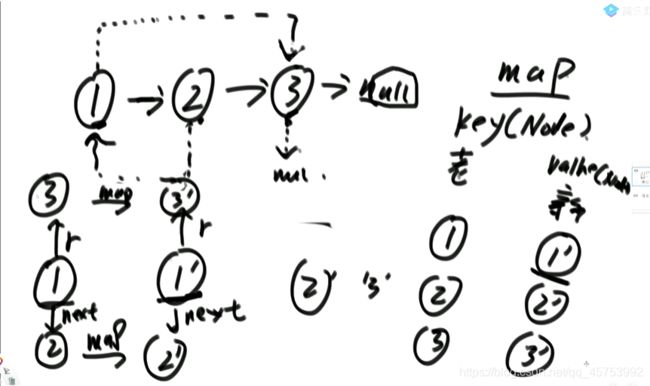
代码展示：

第二种方法：
第一次遍历1，将1’节点插在1之后，再遍历2，将2‘插在2之后，以此类推，插完之后，再一对一对的取值，将1.rand的值赋予1’.rand，以此类推，最后再分离

代码展示：

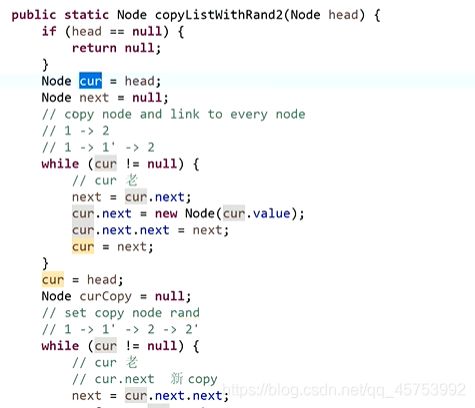
5、

如何找链表中的环开始点：
1、用set集合，遍历一个往set里放一个，在放的同时看遍历的节点set集合里是否已经存在，第一个重复的节点即为环开始的点

2、快慢指针法：先让满指针走1步，快指针走两步，第一次相遇说明有环。相遇后让快指针回起点，继续走，第二次相遇的点即为起点

代码展示：

（1）（无环情况）找到环之后，在让一个链表进入set集合，遍历另一个链表，查遍历到的元素在不在set中，第一个在的即为起点。

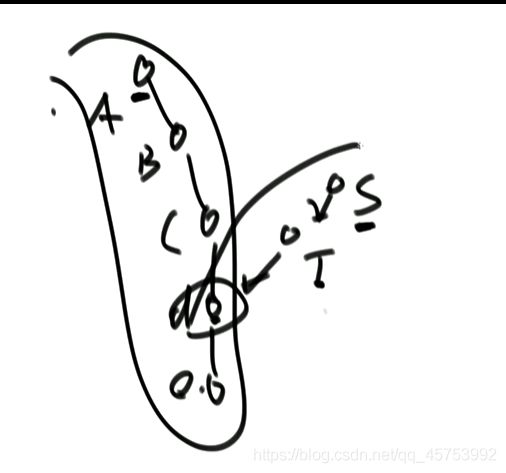
（无环情况）或者先让两个链表都走，得到两个链表的长度，先看最后一个是不是一样的，因为相交的话一定有各个部分，然后再让长链表先向前走长的长度减去短的长度即长度的差值，再然后一起走看什么时候两个节点一样，第一个一样的一定会是初始相交的节点

代码展示：


（2）如果一个有环，另一个无环则不可能相交
（3） 两个链表都有环
有这三种情况，第一种为不相交，第二种为入环节点为同一个，第三种为入环节点不为同一个

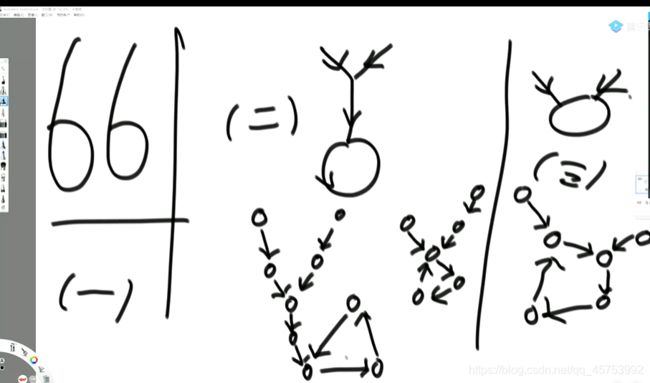
第二种情况：先判断入环节点的地址是否相同，相同的话把入环节点当作终点，接着就可以进行无环情况的操作

区分第一种和第三种：
让第二个入环点往下走，如果它在回来之前能碰到第一个入环点，则为第三种情况，否则为第一种情况。如果为第一种情况，则返回null，如果为第三种情况。则返回loop1（第一个入环点）或者loop2（第二个入环点）

代码展示：


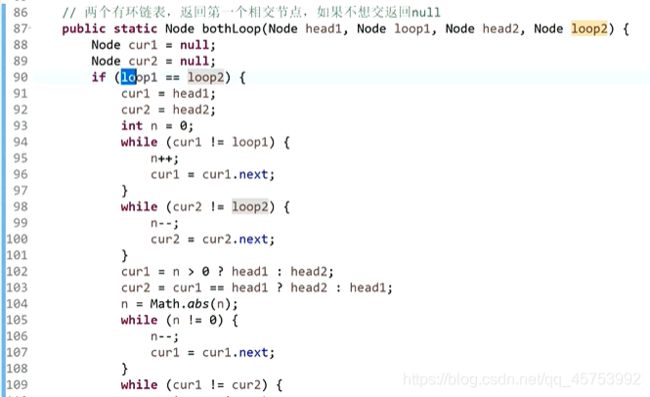
主方法：

6、

1、将要删节点的下一个节点盖到要删的节点上，再指向原节点的后一个节点(不好的操作)

2、错误示例

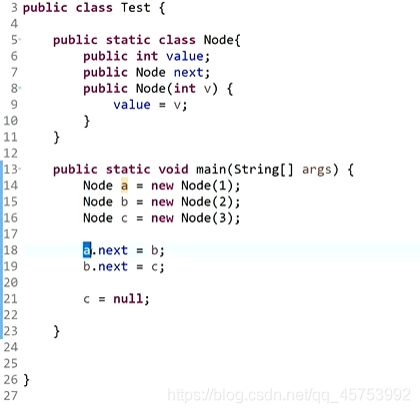
最后只是改变了c的指向，但是内存中的指向仍然不变，所以操作是有问题的

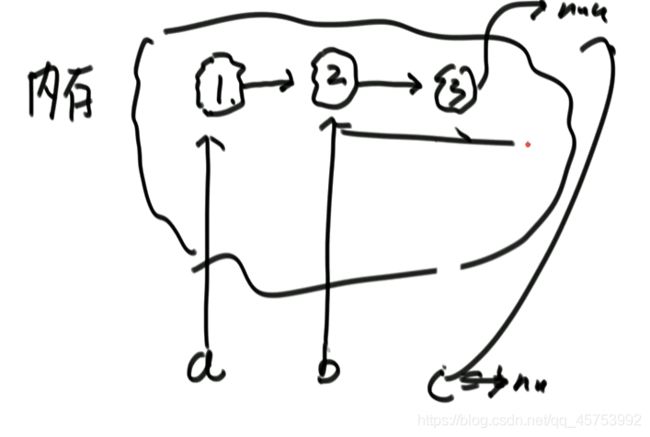
答案：是不行的，要删除节点，必须得给我头节点才行。

二叉树的基本算法

1、结构定义：

2、先序，中序，后序遍历

先序代码展示：
中序代码展示：

后序代码展示：

递归序：每一个结点都会到达三次，按先序把到达结点排序出来

先序就是第一次到达的时候就打印
中序就是第二次到达的时候就打印
后序就是第三次到达的时候就打印
他们都是递归序加工的结果

3、递归实现遍历

4、非递归实现遍历

先序：压栈方法：
（1）弹出就打印
（2）如有右孩子就压入右
（3）如有左就压左

后序：先序的逆序打印就是后序

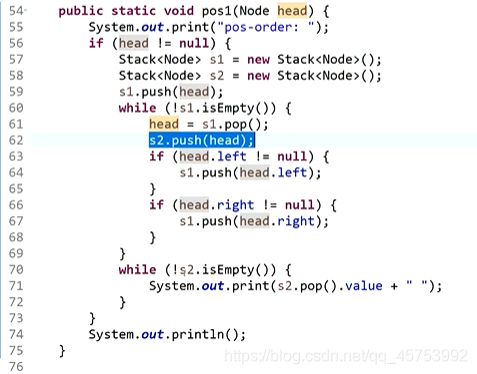
中序：
1、整条左边界依次压入栈
2、1）无法继续，就弹出并打印，进入弹出结点的右子树，继续1）操作

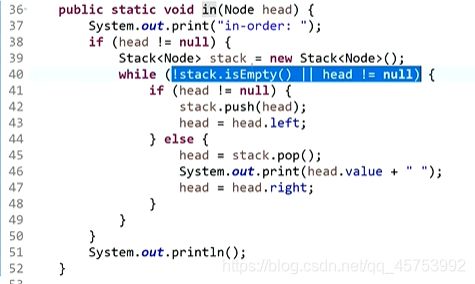
一个栈实现后序遍历：
第一个逻辑分支：当我左树没处理的情况下处理左树
第二个逻辑分支：在左树完成之后再处理右树
第三个逻辑分支：左右都处理完后，处理自己

5、按层遍历

代码展示：

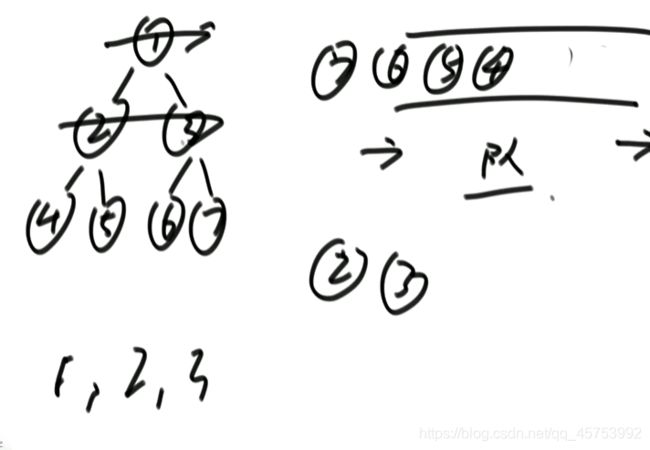
6、找到树中哪一层最宽：
（1）：在结点进队列的时候就记住它的层数



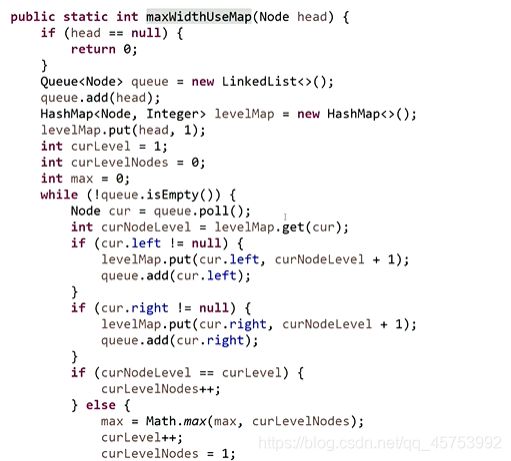
(2)不用map的方法，只用一个队列



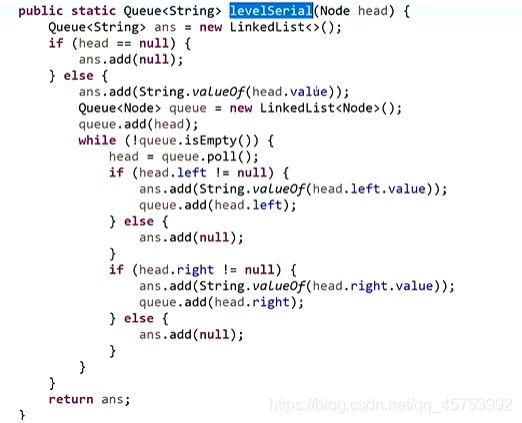
7、二叉树的序列化与反序列化：

先序序列化：不要忽略空

代码展示: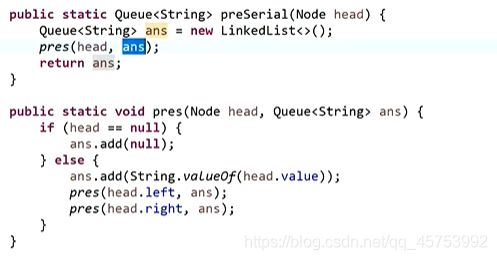

先序反序列化：按先序建，遇空不往下走，走另一边

代码展示：
按层序列化：

代码展示：

孩子为空，就只序列化不加队列，不为空就即加队列。又序列化

反序列化：

代码展示：

8、

最终效果：

代码展示：



9、

后继节点：二叉树的中序遍历中后一位的节点

题解1：从该节点找到头节点，再进行中序遍历找到后继节点

题解2：

代码展示：


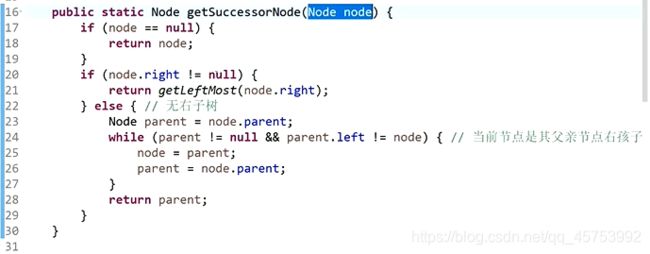
10、


打印的就是这颗树的中序遍历
代码展示：

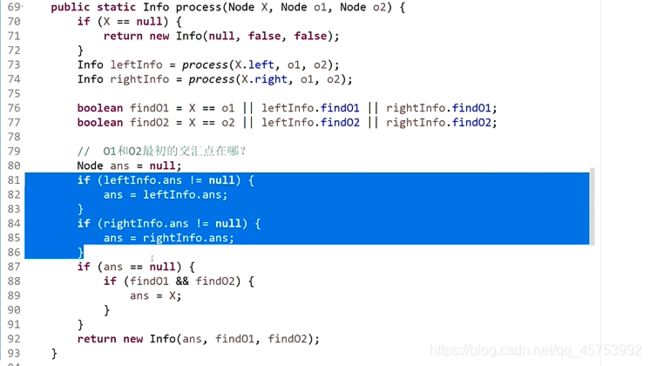
二叉树的递归套路

1、

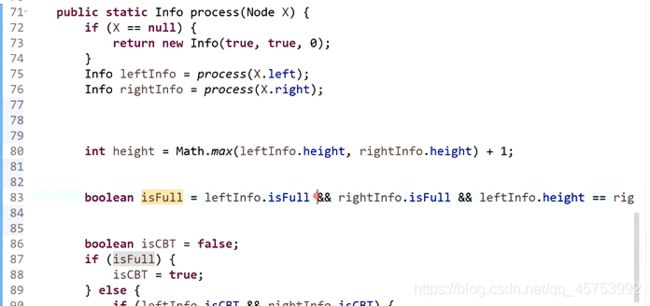
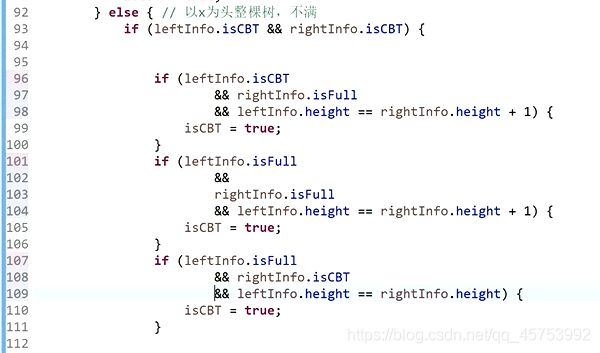
代码展示：


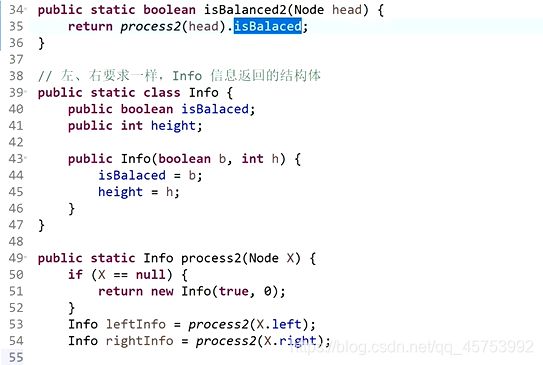
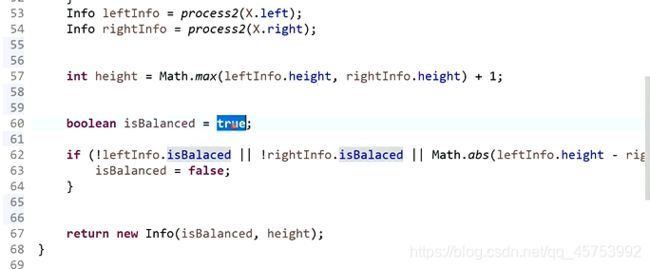
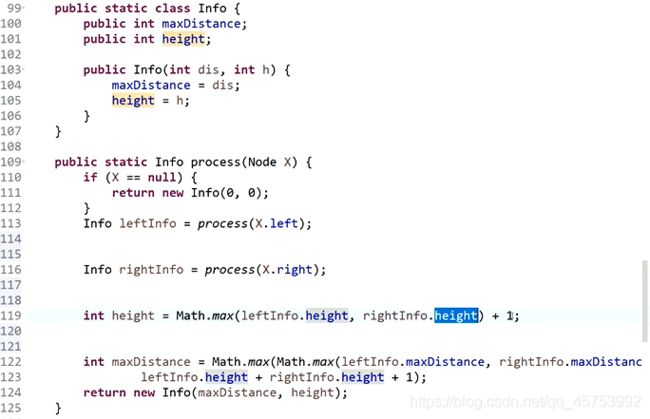
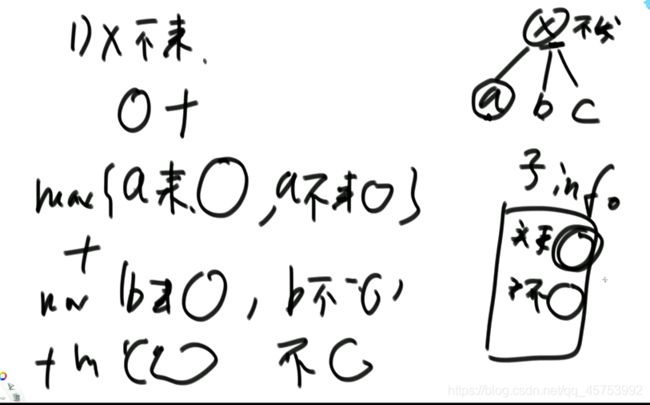
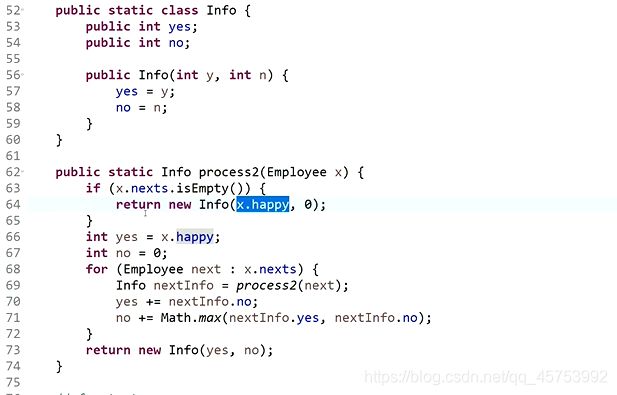
2、
第一种情况：不经过X，就是左树和右树中最大的那颗树

第二种情况：经过X，就是离左边最远到离右边最远，即左树的高度+1+右树的高度

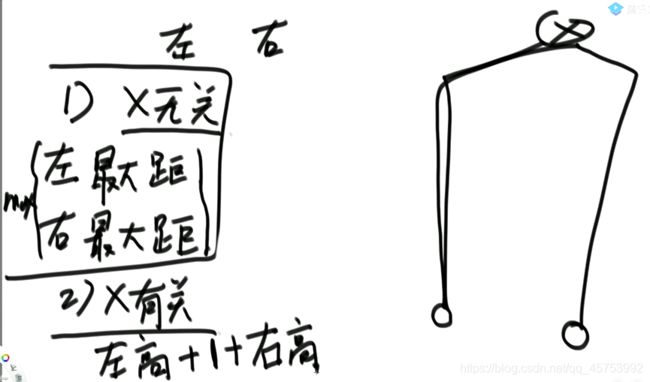
代码展示：

3、

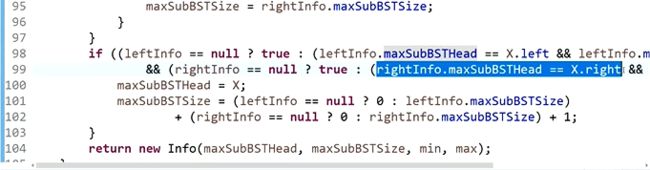
二叉搜索树：左树值比我小，右树值比我大，每颗子树都如此


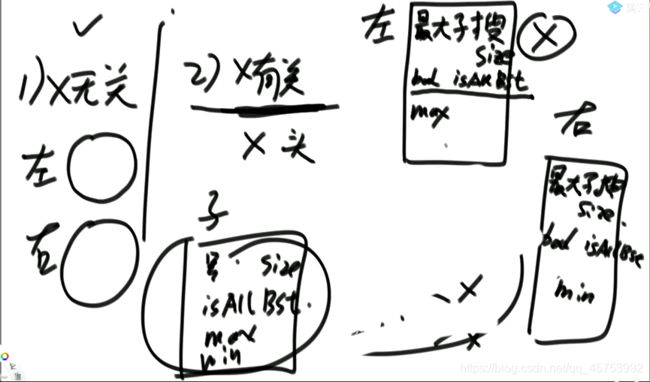
代码展示：


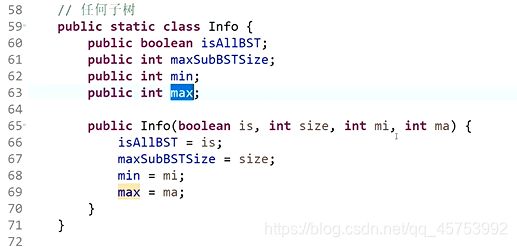
4、

代码展示：


5、


6、

代码展示：

7、


代码展示：

8、

方法1：

先将所有父节点存到哈希表里，然后遍历其中一个节点的父节点，完成后再遍历另一个节点的父节点，直到第一次遇到相同的父节点，返回


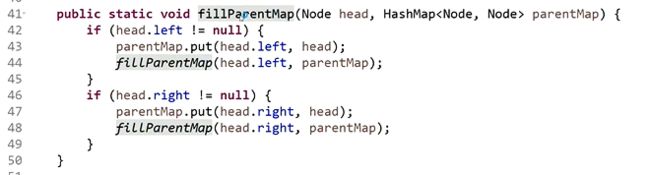
方法2：

代码展示：

贪心算法（不全）

定义

1、
全排列代码（暴力解使用）：

方法2：

并查集（不全）

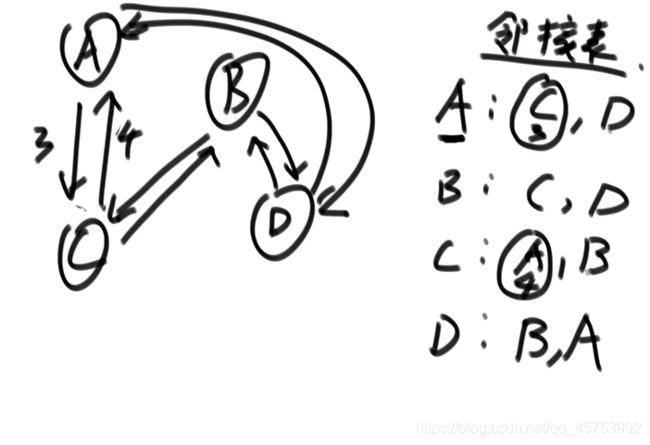
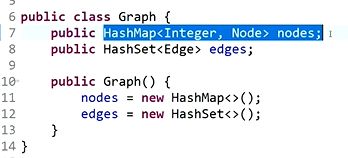
图的算法

推荐图结构：



转换代码：

常见表达方法：


1、

宽度优先：

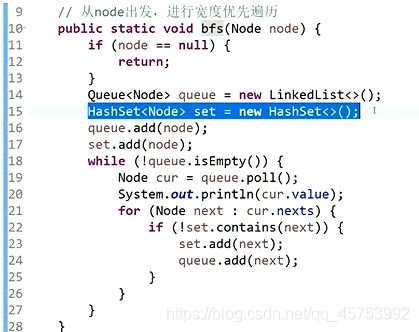
深度优先：

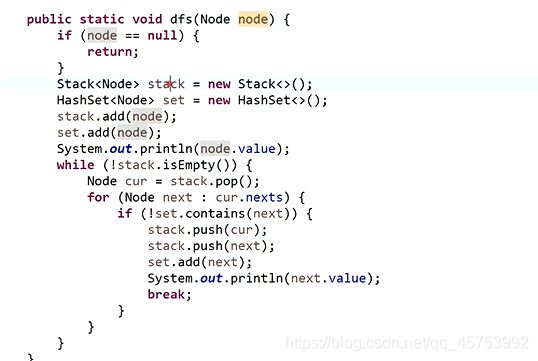
拓扑排序：

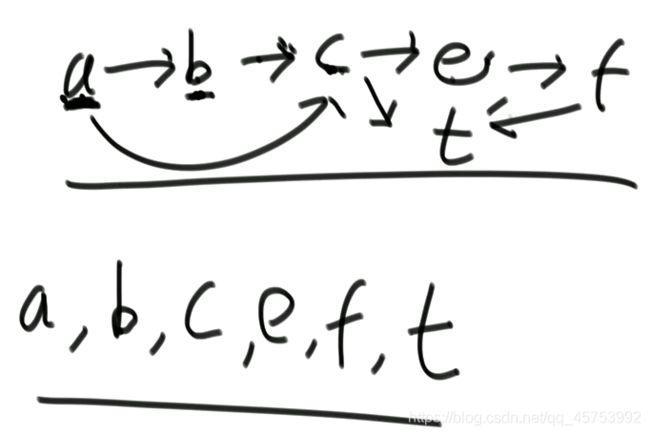
找入度为零的边通过消边实现拓扑排序
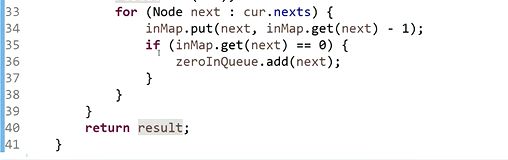
代码展示：


最小生成树：

克鲁斯卡尔算法(需要并查集)：

代码展示：

普瑞姆算法(不需要并查集)：


代码展示：


迪杰斯特拉算法：




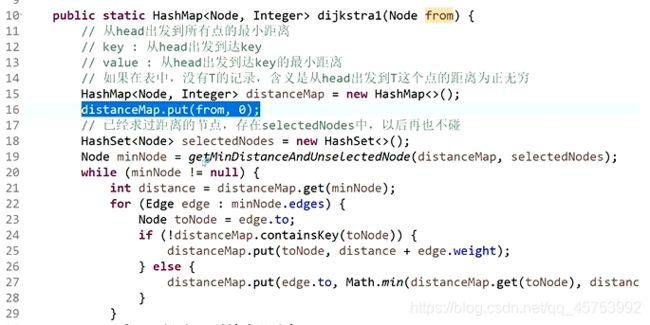
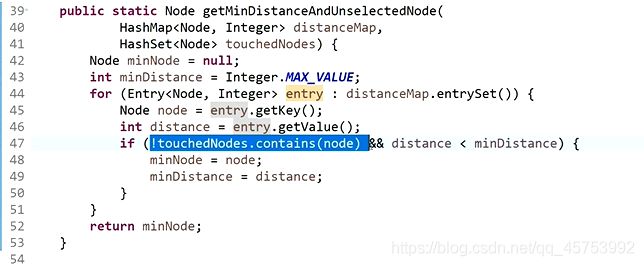方法2（使用堆来实现）：

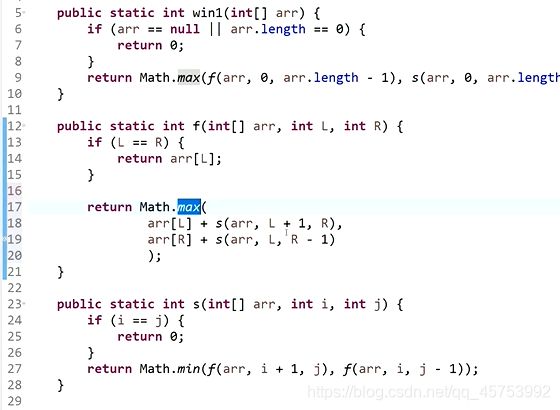
暴力递归

1、

（1）汉诺塔问题：
方法一（复杂，腾路创新）：

方法2（精简）：


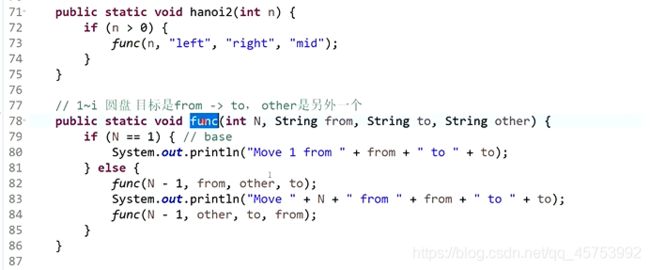
2、


2、打印一个字符串的全部子序列：

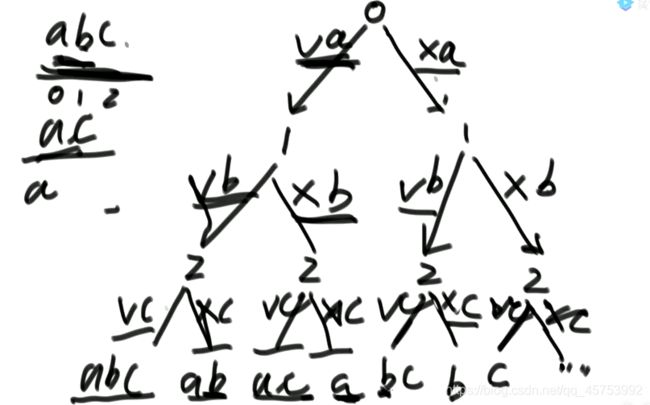
3、打印一个字符串的全部子序列，要求不要出现重复字面值的子序列：

4、打印一个字符串的全部排列：


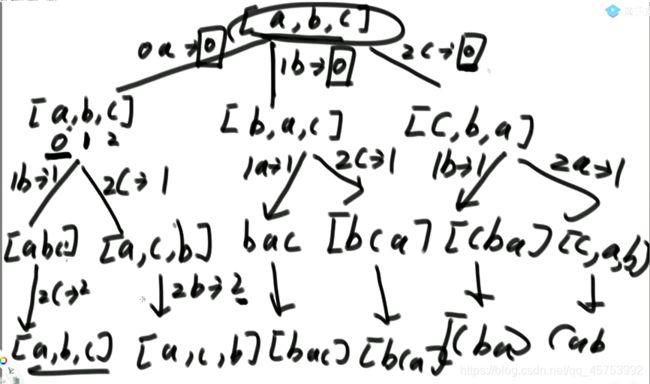
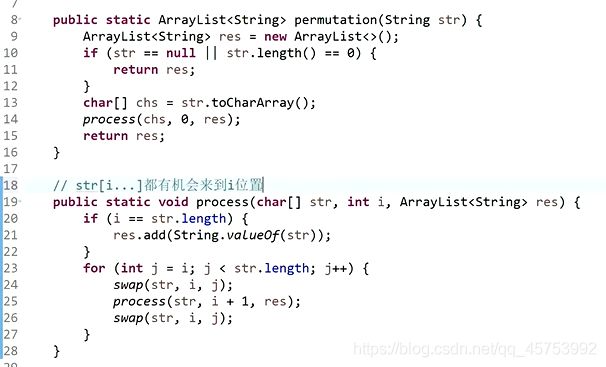
5、打印一个字符串的全部排列，要求不要出现重复的排列：（分支限界）

6、


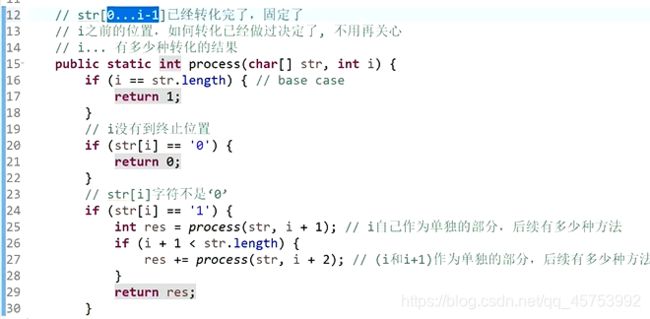
7、

方法1：

方法2、

8、

暴力递归到动态规划

1、

方法1、

方法2、

提取二进制中最右侧的1：a&(~a+1)


方法1、