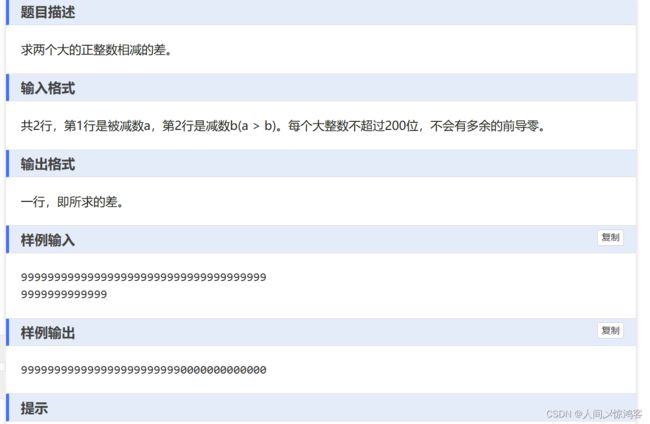
“第六十一天”

 这三个也算一类的，减和加的处理差不多，不过这个题多了限制是被减数大于减数，要是想再完整一点，可以把小于的情况也考虑进去，不过这个我是如果被减数小于减数的话，我就用减数加被减数，然后最后打印的时候加个负号，就多了个if的判断语句。

这个我最开始是直接用double类型做的，因为是整数所以也不会有精度上的问题，运行也是对的，不过不是题的本意应该。

这个感觉应该是题希望的，不过这里有一点还是比较麻烦就是里面的那个for循环，实际上并不需要循环那么多次，但我没有想到这么确定结束循环的条件，可以想一下。

int main()
{
	int n = 0;
	int i = 0;
	scanf("%d", &n);
	int a[100] = { 0 };
	a[99] = 1;
	while (n--)
	{
		int flag = 0;
		for (i = 99;i>=0; i--)
		{
			int x = 2 * a[i] + flag;
			a[i] = x % 10;
			flag = x / 10;
			
		}
	}
	n = 0;
	while (a[n] == 0) n++;
	for (i = n; i < 100; i++)
		printf("%d", a[i]);
	return 0;
}

这个是double类型做的，

int main()
{
	int n = 0;
	scanf("%d", &n);
	int i = 0;
	double m = 1.;
	for (i = 0; i < n; i++)
	{
		m *= 2.0;
	}
	printf("%.0lf", m);
	return 0;
}

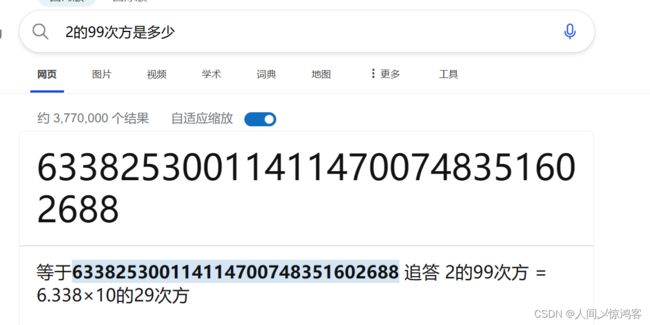
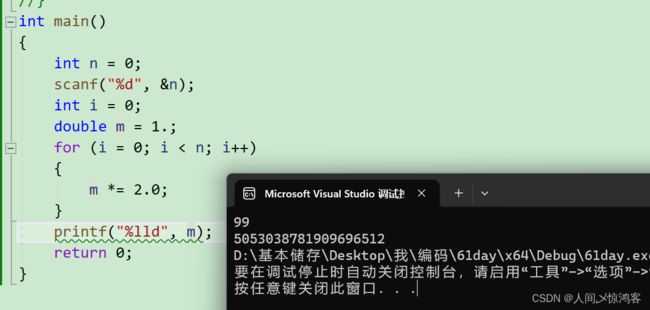
这里是不能转换成整型再打印的，整型存不下（2的99次方需要99比特位），所以下面这个属于数据截断的结果。 

这个没有强制类型转换，但打印的时候会把浮点型的数据直接看成是整型，然后按整型2进制转换成10进制的方法打印出数据（浮点型和整型的存储方式不一样），所以这个就是错的，叫什么我也不知道。

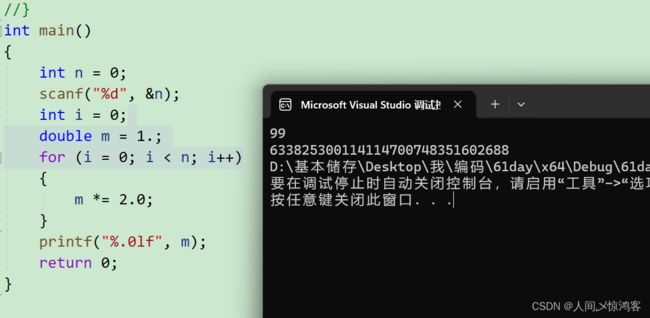
 这个就是没有什么问题了，打印的其实就是浮点型，只不过一位小数都没有打印。

 这个题和求2的n次方没有什么区别，不过把每次乘以的2 变成了 i，不过我真绷不住的是，这个有些结果用10000位都存不下，我用的十万才存的下，不过应该也用不了这么多。

这是我的，改了点，但这个感觉应该运行速度不会和下面差太多，可是实际差的还蛮多的，不知道为什么。错误在把十万打成一万了，这样结果运行成功了，导致if的错误也没发现。

#include

int main()
{
	int n = 0;
	scanf("%d", &n);
	int len = 1;
	int a[100000] = { 0 };
	a[99999] = 1;

	for (int i = 1; i <= n; i++)
	{
		int flag = 0;
		int j = 99999;
		for ( j = 99999; j>=10000-len; j--)//这里一开始是直接让j和0比较大小，控制循环的，也就是每次每个数组元素都要循环，
		{
			int x = a[j] * i + flag;
			a[j] = x % 10;
			flag = x / 10;
		}
		//这里是加的
		if (flag > 0)
		{
			a[j] += flag;
			len++;
		}

	}

	n = 0;
	while (a[n] == 0) n++;
	for (int i = n; i < 100000; i++)
		printf("%d", a[i]);
	return 0;
}

 找到错误了，上面改的什么啊，这个比他的还要快，哈哈哈，上面那个改错了就，然后导致后面的错误也没有发现，就是那个if，后面用while了，注意我使用while循环为什么，是因为阶乘后，flag未必小于10，所以如果使用if的话，最后那个存储的不是个位数，如果n阶n太大，后面会崩掉，用while是把flag化成个位。

int main()
{
	int n = 0;
	scanf("%d", &n);
	int len = 1;
	int a[100000] = { 0 };
	a[99999] = 1;

	for (int i = 1; i <= n; i++)
	{
		int flag = 0;
		int j = 99999;
		for (j = 99999; j >= 100000 - len; j--)//这里一开始是直接让j和0比较大小，控制循环的，也就是每次每个数组元素都要循环
		{
			int x = a[j] * i + flag;
			a[j] = x % 10;
			flag = x / 10;
		}
		//这里是加的
		while (flag > 0)
		{
			a[j--] += flag%10;
			flag /= 10;
			len++;
		}

	}

	
	for (int i = 100000-len; i < 100000; i++)
		printf("%d", a[i]);
	return 0;
}

 这个是最开始的，可以看看为什么这个不会向上面那样崩掉

#include
int main()
{
    int n = 0;
    scanf("%d", &n);
 
    int a[100000] = { 0 };
    a[99999] = 1;
 
    for (int i = 1; i <= n; i++)
    {
        int flag = 0;
         
        for (int j = 99999; j >=0; j--)
        {
            int x = a[j] * i + flag;
            a[j] = x % 10;
            flag = x / 10;
        }
    }
 
    n = 0;
    while (a[n] == 0) n++;
    for (int i = n; i < 100000; i++)
        printf("%d", a[i]);
    return 0;
}

这个是人家的，人家从低位开始算，算的时候记着长度，所以总循环次数比我少很多

#include

int main()

{

     int n,i,j,k,len=1,a[100000]={0};//len长度一开始定为 1 

     scanf("%d",&n);

     a[1]=1;

     for(i=1;i<=n;i++)//要乘的数

     {

            for(j=1;j<=len;j++)//len表示有效数组的长度 

             {

                  a[j]*=i;//先把每一位算出来再存 例如：a数组为12345  i=35时  a[j]*i即    1*35  2*35  3*35  4*35  5*35     a数组后来为 35 70 105   140  175

             } 



             for(k=1;k<=len;k++)/*转为十进制存储  35进3余5  70+3=73 进7余3  105+7=112进11 余2 140+11=151进15 余1  175+15=190 进19 余0  a数组后来为  进制+余数 再求余，得到的余数就是a数组存储的十进制结果 。即   5    3    2   1   0*/     

             {

                 if(a[k]>9)//需要进位的情况 

                 {

                     a[k+1]+=a[k]/10;

                     a[k]%=10;

                     if(a[k+1]!=0&&k==len)

                     {    

                     len++;//最高位需要进位 

                     }

                 }

            }

     }

     for(i=len;i>=1;i--)

     {

         printf("%d",a[i]);

     } 

     return 0;

}