Pytorch：矩阵乘法总结

1、矩阵相乘

（1）二维矩阵乘法：torch.mm(mat1, mat2, out=None) → Tensor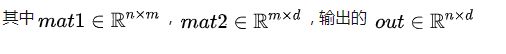

该函数一般只用来计算两个二维矩阵的矩阵乘法，并且不支持broadcast操作。

代码例子：对应行列乘

In[30]: mat1 = t.Tensor([[1,2,3],[2,3,4]])
   ...: mat2 = t.Tensor([[1,2,3],[2,3,4],[3,4,5]])
   ...: t.mm(mat1, mat2)
Out[30]: 
tensor([[14., 20., 26.],
        [20., 29., 38.]])

In[32]: mat1
Out[32]: 
tensor([[1., 2., 3.],
        [2., 3., 4.]])
In[33]: mat2
Out[33]: 
tensor([[1., 2., 3.],
        [2., 3., 4.],
        [3., 4., 5.]])

   ...: t.mm(mat1, mat2)

（2）三维带batch的矩阵乘法：torch.matmul(mat1, mat2, out=None) → Tensor
由于神经网络训练一般采用mini-batch，经常输入的时三维带batch的矩阵，所以提供

该函数的两个输入必须是三维矩阵并且第一维相同（表示Batch维度）， 不支持broadcast操作。

 

（3）多维矩阵乘法： torch.matmul()

支持broadcast操作，使用起来比较复杂。针对多维数据 matmul() 乘法，可以认为该乘法使用使用两个参数的后两个维度来计算，其他的维度都可以认为是batch维度。假设两个输入的维度分别是input(1000×500×99×111000×500×99×11), other(500×11×99500×11×99)那么我们可以认为torch.matmul(input, other, out=None)乘法首先是进行后两位矩阵乘法得到(99×11)×(11×99)⇒(99×99)(99×11)×(11×99)⇒(99×99) ，然后分析两个参数的batch size分别是 (1000×500)(1000×500) 和 500500 , 可以广播成为 (1000×500)(1000×500)， 因此最终输出的维度是(1000×500×99×991000×500×99×99)。

 

代码示例:

import torch
a=torch.randn(2,3)
b=torch.randn(3,2)
print(torch.mm(a,b))
print(torch.matmul(a,b))

2.矩阵逐元素相乘（点乘），对应位置相乘

torch.mul(mat1, other, out=None)
点乘不求和操作，又可以叫作Hadamard product；点乘再求和，即为卷积。

代码：

In[22]: tensor = t.Tensor([[1,2], [3,4], [5, 6]])
In[23]: tensor
Out[23]: 
tensor([[1., 2.],
        [3., 4.],
        [5., 6.]])
In[24]: tensor.mul(tensor)
Out[24]: 
tensor([[ 1.,  4.],
        [ 9., 16.],
        [25., 36.]])

另外：
@是用来对tensor进行矩阵相乘的：x@w

*用来对tensor进行矩阵进行逐元素相乘：x*w

x = x.mm(self.w) #x@W等价于x.mm(w)